Design of Fast Differential Frequency Measurement System Based on FPGA
-
摘要:
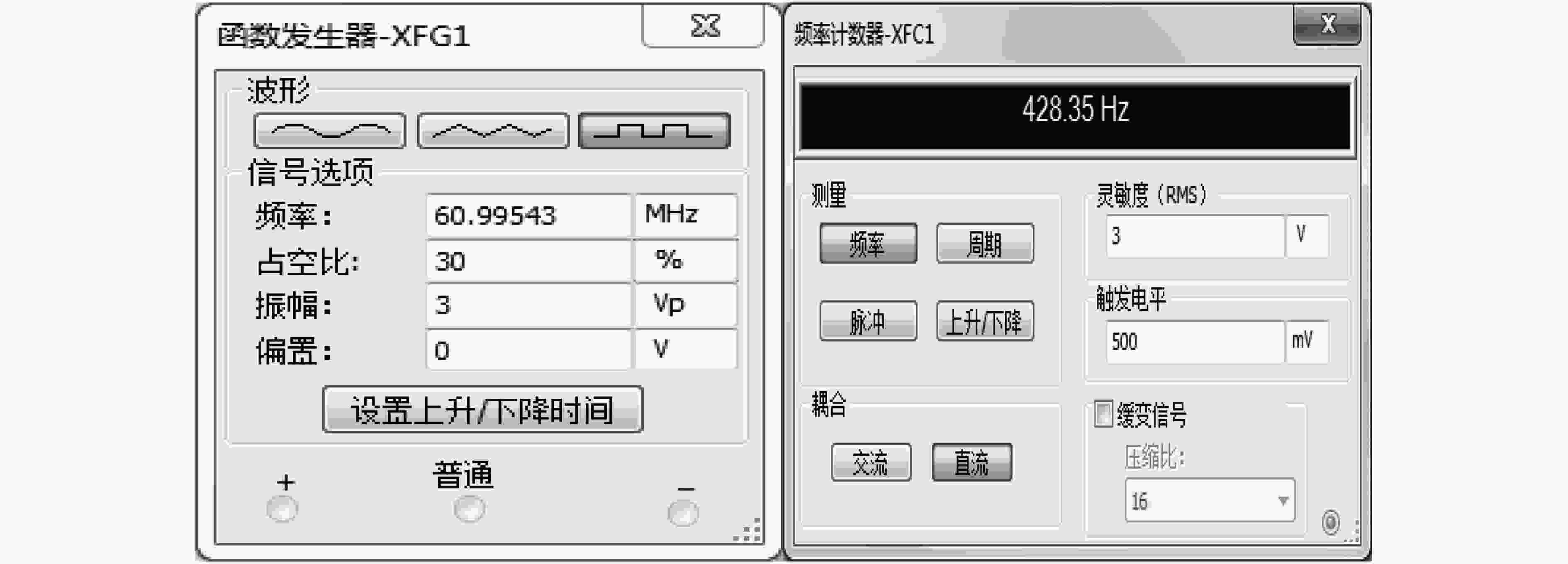
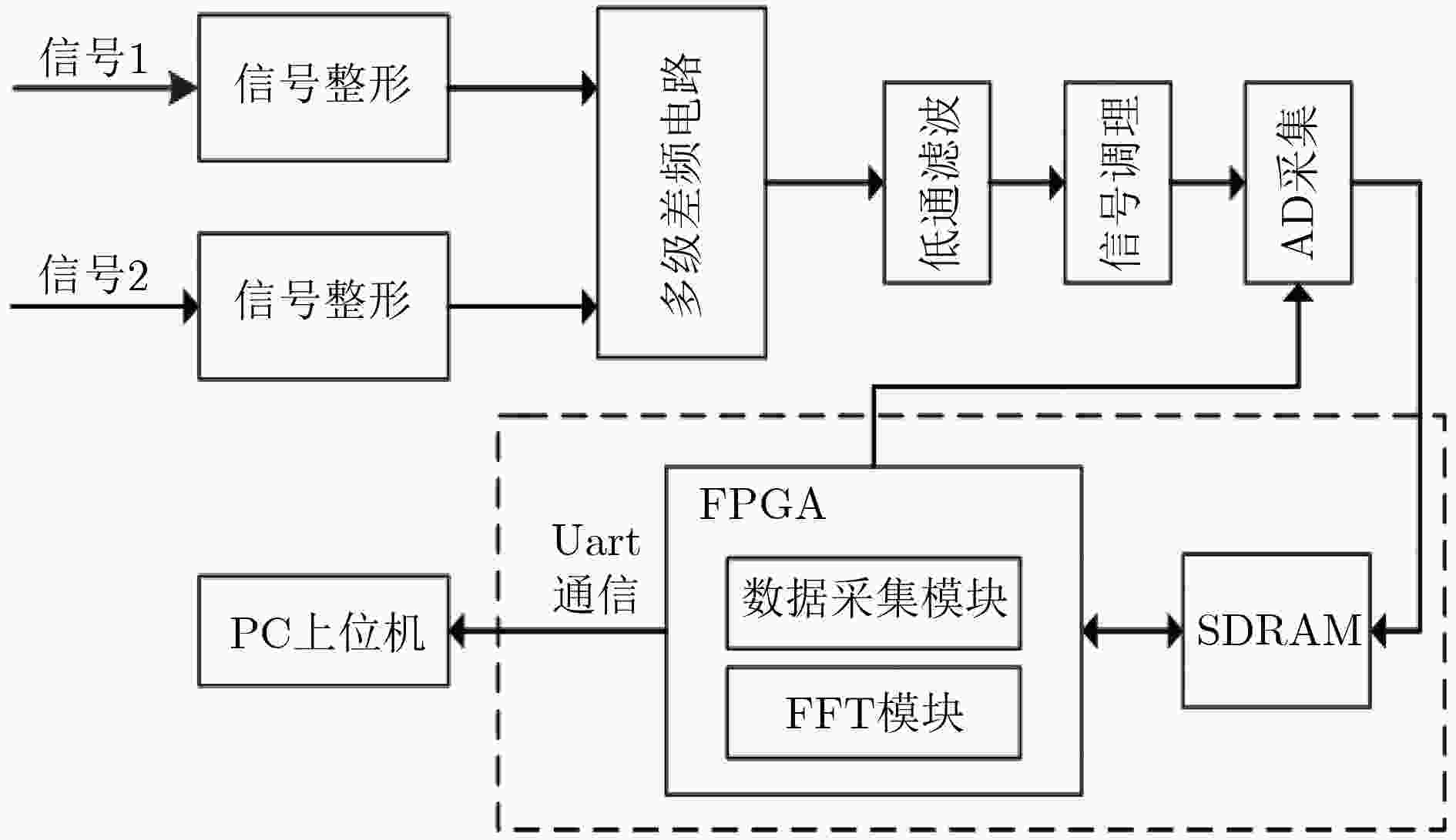
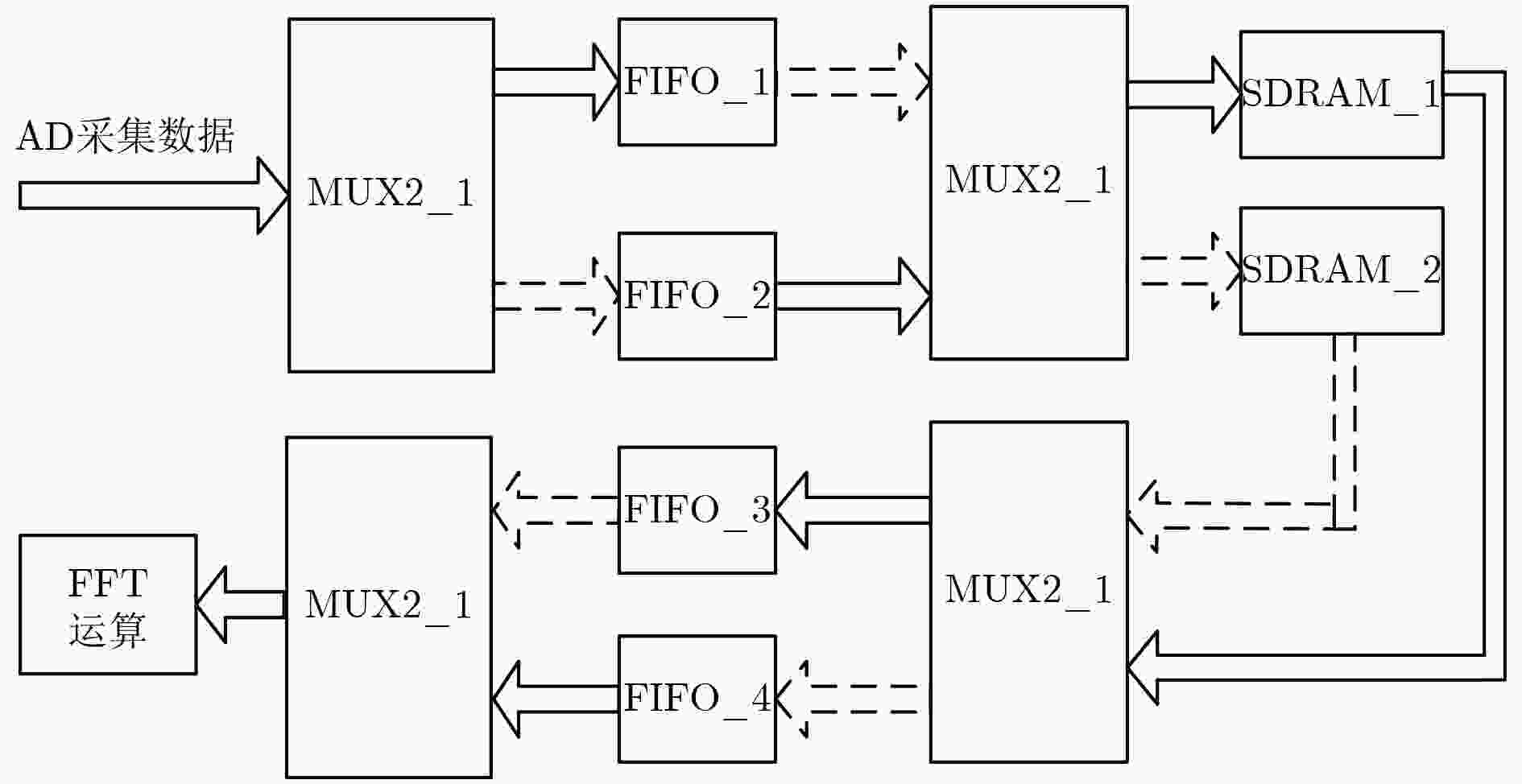
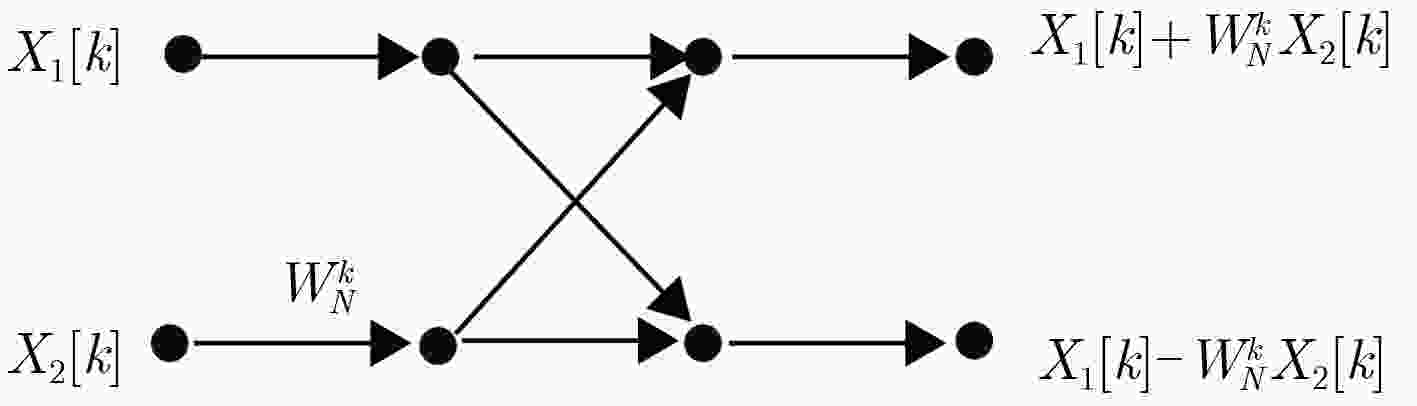
针对电子测量中如何对基频较高而频率变化值较小的动态信号进行高精度频率测量的问题,引入了差频测量的方法。该文提出一种新型的动态可调的多级差频电路结构,设计了基于FPGA的快速差频测量系统,通过在FPGA上设计快速傅里叶变换(FFT)算法来实现系统的数据处理功能。仿真结果表明,在满足差频条件的基础上,合理设计多级差频电路的结构能够实现高精度频率测量,在进行信号频谱分析时能得到较为准确的结果。实验验证了该测量系统能够实现快速FFT运算,相比于MATLAB软件平台,在数据处理效率上有明显的优势;同时在性能指标满足数据采集要求的前提下,系统可动态调整FFT模型的结构来适应不同规模点数FFT运算的需求。
Abstract:For the problem of high precision frequency measurement of dynamic signals with high fundamental frequency and small frequency change value in electronic measurement, a method of differential frequency measurement is introduced. A novel dynamic adjustable multi-stage frequency-difference circuit structure is proposed. The fast differential frequency measurement system based on FPGA is used to design the Fast Fourier Transform (FFT) algorithm on the FPGA to realize the data processing function of the system. The simulation and experimental results show that the structure of the multi-stage differential frequency circuit can be designed with high precision frequency, and the result can be obtained when the spectrum analysis is carried out. The system can realize the fast FFT operation. Compared with the MATLAB software platform, the system has obvious advantages in the efficiency of data processing. The structure of the FFT model can be dynamically adjusted to meet the requirements of FFT operation of different scale points, and the system performance index can meet the requirements of data acquisition system.
-
Key words:
- Differential frequency measurement /
- FPGA /
- FFT
-
表 1 差频电路实验测量数据
fin=35.00005 kHz 理论频差(kHz) 实测频差(kHz) 绝对误差(Hz) 相对误差(%) fck/fin fck (kHz) 0.660011 23.100414 11.899636 11.200800 698.836 5.872751 0.663334 23.216715 11.783335 11.433400 349.935 2.969745 0.666668 23.333414 11.666636 11.666700 0.064 0.000549 0.670002 23.450113 11.549937 11.549900 0.037 0.000320 0.673337 23.566816 11.433234 11.433200 0.034 0.000297 0.733337 25.666827 9.333223 9.333200 0.023 0.000246 0.800003 28.000136 6.999914 6.999600 0.314 0.004486 0.866672 30.333548 4.666502 4.666500 0.002 0.000043 0.933337 32.666858 2.333192 2.333200 0.008 0.000343 0.980003 34.300166 0.699884 0.699890 0.006 0.000857 0.990003 34.650168 0.349882 0.349894 0.012 0.003430 1.000003 35.000172 0.000122 0.000132 0.010 8.196721 1.020004 35.700174 0.700124 0.700109 0.015 0.002142 1.200004 42.000206 7.000156 7.000034 0.122 0.001743 1.400005 49.000243 14.000193 14.000069 0.124 0.000886 1.600006 56.000277 21.000227 21.000000 0.227 0.001081 1.800007 63.000318 28.000268 28.000140 0.128 0.000457 1.980007 69.300355 34.300305 34.300280 0.025 0.000073 1.990099 69.653570 34.653520 34.530000 123.520 0.356443 2.000010 70.000463 35.000413 34.640000 360.410 1.029739 2.010011 70.350470 35.350420 34.880000 470.420 1.330734 2.020011 70.700478 35.700428 35.000000 700.428 1.961960 表 2 差频测量系统和MATLAB数据处理效率
点数 采样频率/待测频率 分辨率(Hz) 相对误差(%) 时间消耗 差频测量系统t1×10–6 (s) MATALB t2 (s) t2/t1 64 1.5 8.44 65.12 1.7911 0.0728 40645.41 2.5 14.06 2.77 1.7911 0.0729 40701.25 3.5 19.69 4.59 1.7912 0.0729 40698.97 128 1.5 4.22 71.11 3.1821 0.0824 25894.85 2.5 7.03 1.44 3.1823 0.0825 25924.65 3.5 9.84 2.51 3.1921 0.0824 25813.73 256 1.5 2.11 68.87 5.4661 0.0927 16959.08 2.5 3.52 1.24 5.4654 0.0928 16979.54 3.5 4.92 1.35 5.4657 0.0928 16978.61 512 1.5 1.05 71.12 10.9351 0.1084 9913.03 2.5 1.76 1.02 10.9332 0.1083 9905.61 3.5 2.46 1.12 10.9411 0.1084 9907.60 表 3 量化位数对FFT的影响
量化位数 信噪比(dB) 16 27.10 32 67.83 64 98.43 表 4 差频测量系统测量误差及分辨率
ft (kHz) 闸门个数 计数器计数值 fck–fin (Hz) fin (Hz) 相对误差(×10–6) 分辨率(×10–6) 170.00039 2000 7999371 2000.26227 170000.7777 2.2808 5.81575 170.20039 1800 7999165 1800.28240 170200.7576 2.1598 5.81619 170.40039 1600 7999747 1600.13460 170400.9054 3.0246 5.81629 170.60038 1400 7998135 1400.39997 170600.6418 1.5345 5.81673 170.80039 1200 7998931 1200.22338 170800.8166 2.4978 5.81521 171.00039 1000 7987647 1001.59909 170999.4409 5.5502 5.81764 -
李存龙, 陈伟民, 章鹏, 等. 采用差频技术的正弦调制型微波测距系统研究[J]. 电子测量与仪器学报, 2014, 28(1): 17–21. doi: 10.13382/j.jemi.2014.01.003LI Cunlong, CHEN Weimin, Zhang Peng, et al. Research on sinusoidal modulation microwave ranging system based on heterodyne technique[J]. Journal of Electronic Measurement and Instrument, 2014, 28(1): 17–21. doi: 10.13382/j.jemi.2014.01.003 冯冠平. 谐振传感理论及器件[M]. 北京: 清华大学出版社, 2008: 35–40.FENG Guanping. Resonant Sensor Theory and Device[M]. Beijing: Tsinghua University Press, 2008: 35–40. 樊养余, 李利品, 党瑞荣. 基于随机共振的任意大频率微弱信号检测方法研究[J]. 仪器仪表学报, 2013, 34(3): 566–572. doi: 10.3969/j.issn.0254-3087.2013.03.013FAN Yangyu, LI Lipin, and Dang Ruirong. Study on high frequency weak signal detection method based on stochastic resonance[J]. Chinese Journal of Scientific Instrument, 2013, 34(3): 566–572. doi: 10.3969/j.issn.0254-3087.2013.03.013 王盟盟, 董瑞芳, 项晓, 等. 基于外差检测原理的绝对测距性能理论研究[J]. 仪器仪表学报, 2016, 37(8): 1861–1868. doi: 10.3969/j.issn.0254-3087.2016.08.018WANG Mengmeng, DONG Ruifang, XIANG Xiao, et al. Theoretical research for absolute distance measurement based on heterodyne detection principle[J]. Chinese Journal of Scientific Instrument, 2016, 37(8): 1861–1868. doi: 10.3969/j.issn.0254-3087.2016.08.018 刘婉茹, 叶建芳, 孙一萍. 基于Multisim乘法器混频电路的仿真研究[J]. 微型电脑应用, 2016, 32(10): 48–50. doi: 10.3969/j.issn.1007-757X.2016.10.014LIU Wanru, YE Jianfang, and SUN Yiping. Simulation and study of multiplier mixer circuit based on multism[J]. Microcomputer Applications, 2016, 32(10): 48–50. doi: 10.3969/j.issn.1007-757X.2016.10.014 LIN Ningning, MENG Xiaofeng, and NIE Jing. Dew point calibration system using a quartz crystal sensor with a differential frequency method[J]. Sensors, 2016, 16(11): 1944–1948. doi: 10.3390/s16111944 程坤, 黄庆安, 秦明, 等. 一种简单实用的差频方法原理研究及应用[J]. 电子器件, 2006, 29(2): 473–475. doi: 10.3969/j.issn.1005-9490.2006.02.046CHENG Kun, HUANG Qingan, QIN Ming, et al. Simple method of improving the differential frequency using D flip-flop[J]. Chinese Journal of Electron Devices, 2006, 29(2): 473–475. doi: 10.3969/j.issn.1005-9490.2006.02.046 徐洋洋. 基于FPGA的多通道大容量FIFO设计[J]. 电子测量技术, 2017, 40(8): 193–197. doi: 10.19651/j.cnki.emt.2017.08.043XU Yangyang. Design of multi-channel FIFO with mass storage facility based on FPGA[J]. Electronic Measurement Technology, 2017, 40(8): 193–197. doi: 10.19651/j.cnki.emt.2017.08.043 梁晨, 赵邦信. 基于FPGA和DDR3 SDRAM的大规模查找表设计与实现[J]. 电子器件, 2017, 40(4): 849–855. doi: 10.3969/j.issn.1005-9490.2017.04.014LIANG Chen and ZHAO Bangxin. Design of large-scale look-up table based on FPGA and DDR3 SDRAM[J]. Chinese Journal of Electron Devices, 2017, 40(4): 849–855. doi: 10.3969/j.issn.1005-9490.2017.04.014 梁华国, 孙红云, 孙骏, 等. 一种基于FPGA的微处理器软错误敏感性分析方法[J]. 电子与信息学报, 2017, 39(1): 245–249. doi: 10.11999/JEIT.160225LIANG Huaguo, SUN Hongyun, SUN Jun, et al. FPGA-based soft error sensitivity analysis method for microprocessor[J]. Journal of Electronics &Information Technology, 2017, 39(1): 245–249. doi: 10.11999/JEIT.160225 WANG Jiawei, YU Le, and YANG Haigang. FPGA based multi-channel variable-length FFT implementation[J]. Journal of Terahertz Science and Electronic Information Technology, 2017, 15(3): 469–474. doi: 10.11805/TKYDA201703.0469 陈杰男, 费超, 袁建生, 等. 超高速全并行快速傅里叶变换器[J]. 电子与信息学报, 2016, 38(9): 2410–2414. doi: 10.11999/JEIT160036CHEN Jienan, FEI Chao, YUAN Jiansheng, et al. An ultra-high-speed fully-parallel fast fourier transform design[J]. Journal of Electronics &Information Technology, 2016, 38(9): 2410–2414. doi: 10.11999/JEIT160036 CHEN Jiyang, YUAN Wulei, YUAN Xipeng, et al. Configurable floating-point FFT accelerator on FPGA based multiple-rotation CORDIC[J]. Chinese Journal of Electronics, 2016, 25(6): 1063–1070. doi: 10.1049/cje.2016.08.002 黄志洪, 李威, 杨立群, 等. 一种基于与非锥簇架构 FPGA 输入交叉互连设计优化方法[J]. 电子与信息学报, 2016, 38(9): 2397–2404. doi: 10.11999/JEIT151216HUANG Zhihong, LI Wei, YANG Liqun, et al. An input crossbar optimization method for and-inveter cone based FPGA[J]. Journal of Electronics &Information Technology, 2016, 38(9): 2397–2404. doi: 10.11999/JEIT151216 苏斌, 刘畅, 潘志刚. 基于FPGA的高速浮点FFT/IFFT处理器设计与实现[J]. 中国科学院大学学报, 2015, 32(2): 259–263. doi: 10.7523/j.issn.2095-6134.2015.02.016SU Bin, LIU Chang, and PAN Zhigang. Design and implementation on high-speed floating points FFT processor based on FPGA[J]. Journal of University of Chinese Academy of Sciences, 2015, 32(2): 259–263. doi: 10.7523/j.issn.2095-6134.2015.02.016 施佺, 韩赛飞, 黄新明, 等. 面向全同态加密的有限域FFT算法FPGA设计[J]. 电子与信息学报, 2018, 40(1): 57–62. doi: 10.11999/JEIT170312SHI Quan, HAN Saifei, HUANG Xinming, et al. Design of finite field FFT for fully homomorphic encryption based on FPGA[J]. Journal of Electronics &Information Technology, 2018, 40(1): 57–62. doi: 10.11999/JEIT170312 -






 下载:
下载:

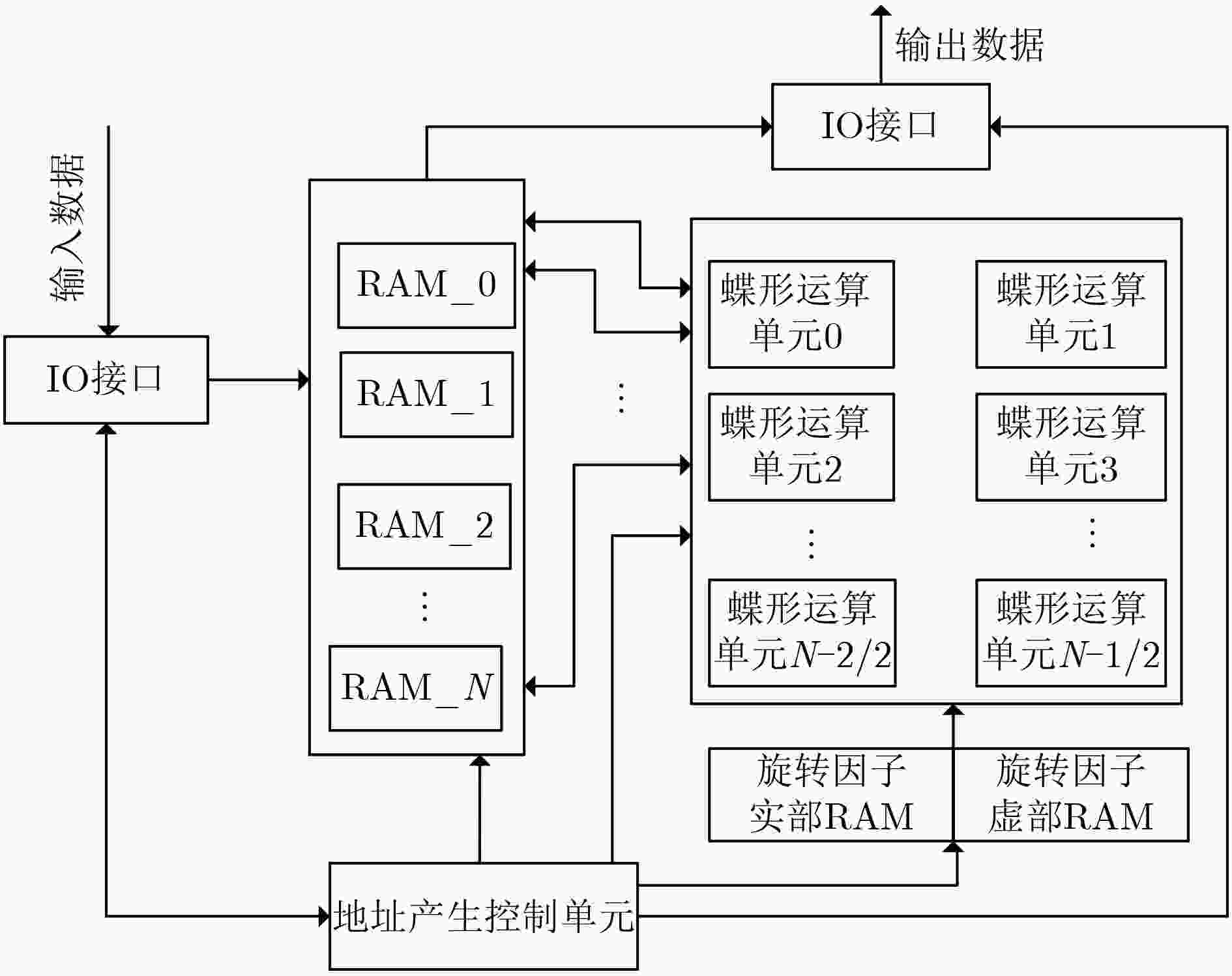
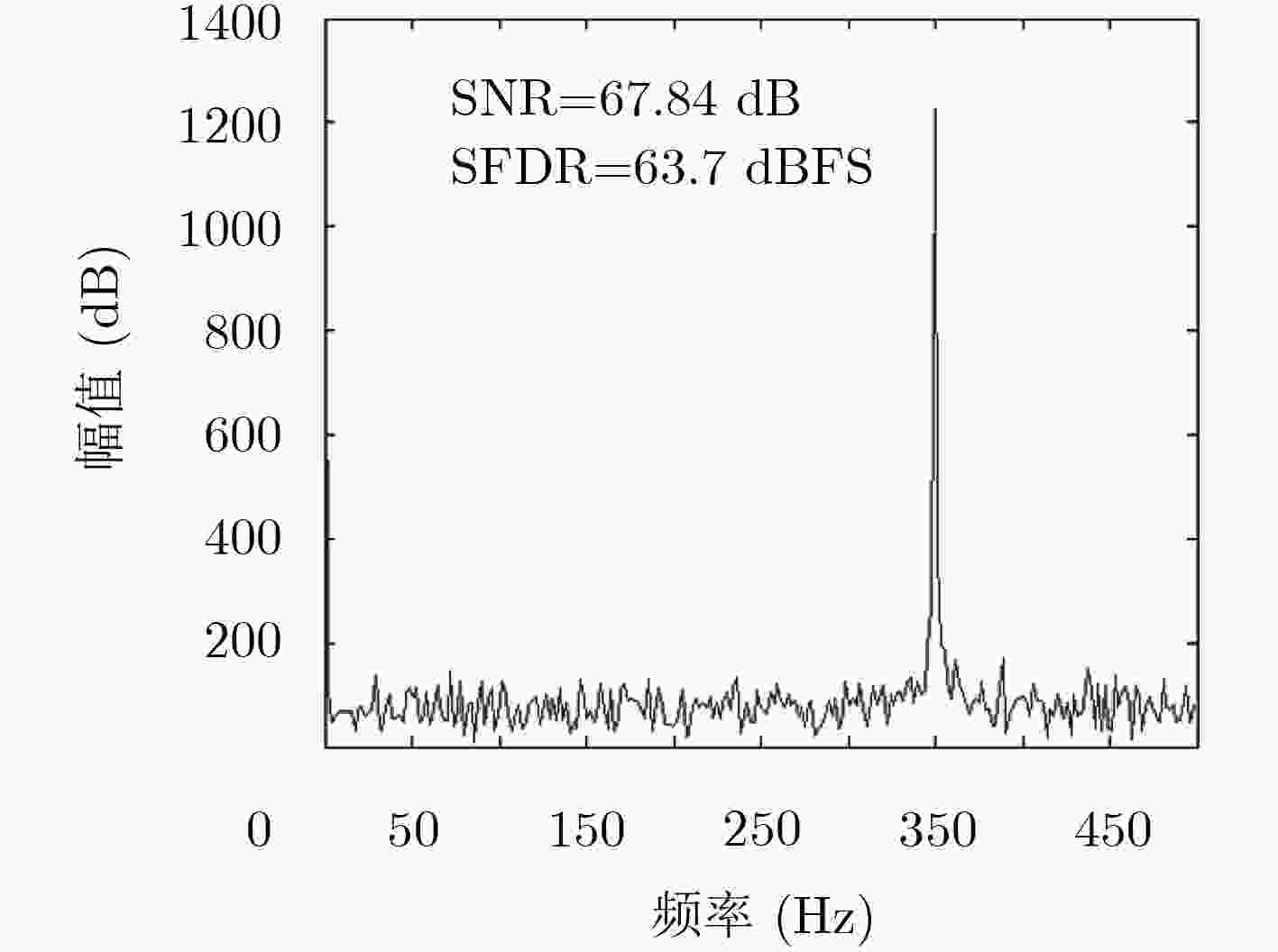
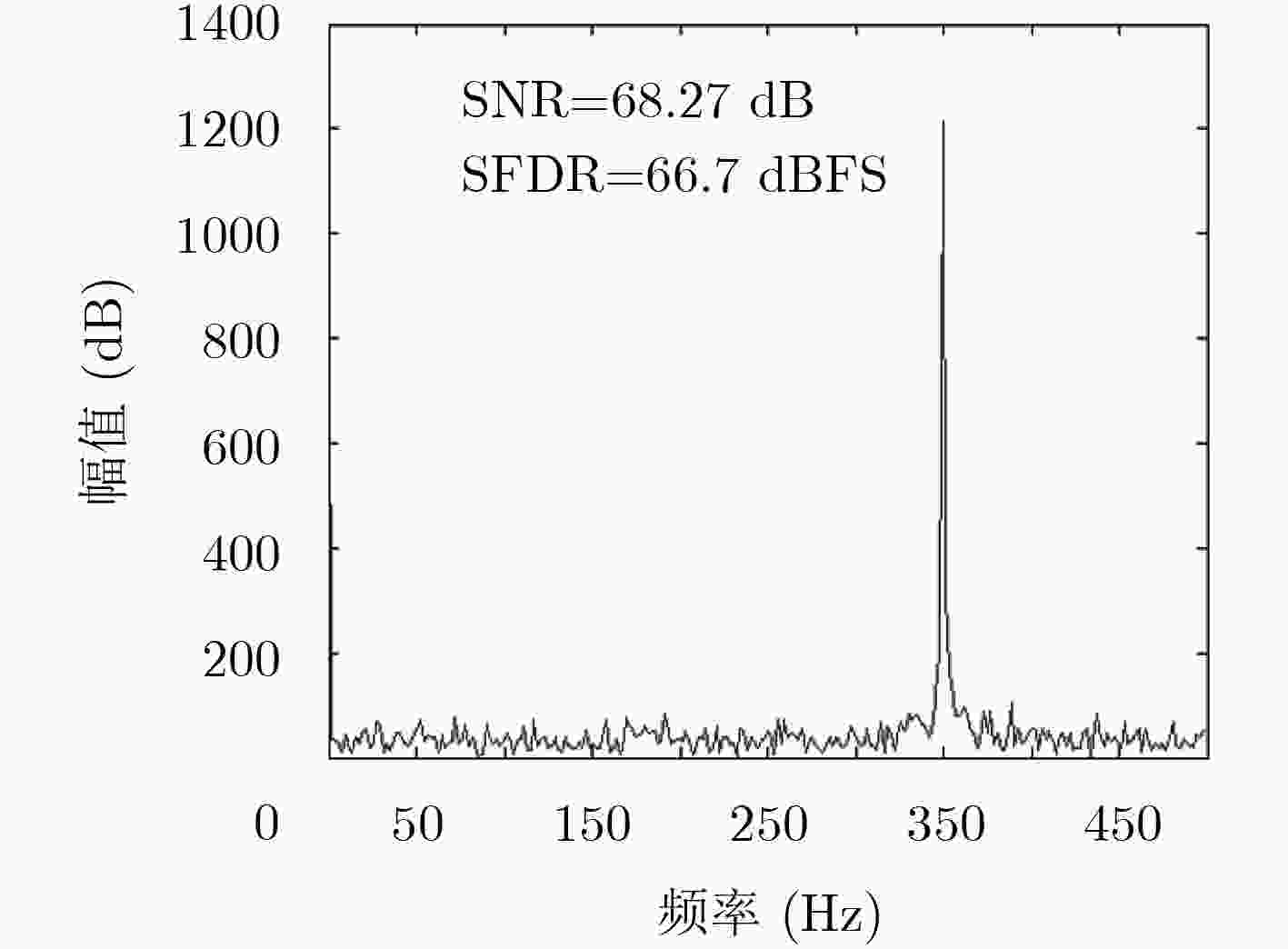


 下载:
下载:
