Single Channel Blind Separation Performance Bound of Non-cooperative Received Paired Carrier Multiple Access Mixed Signal
-
摘要:
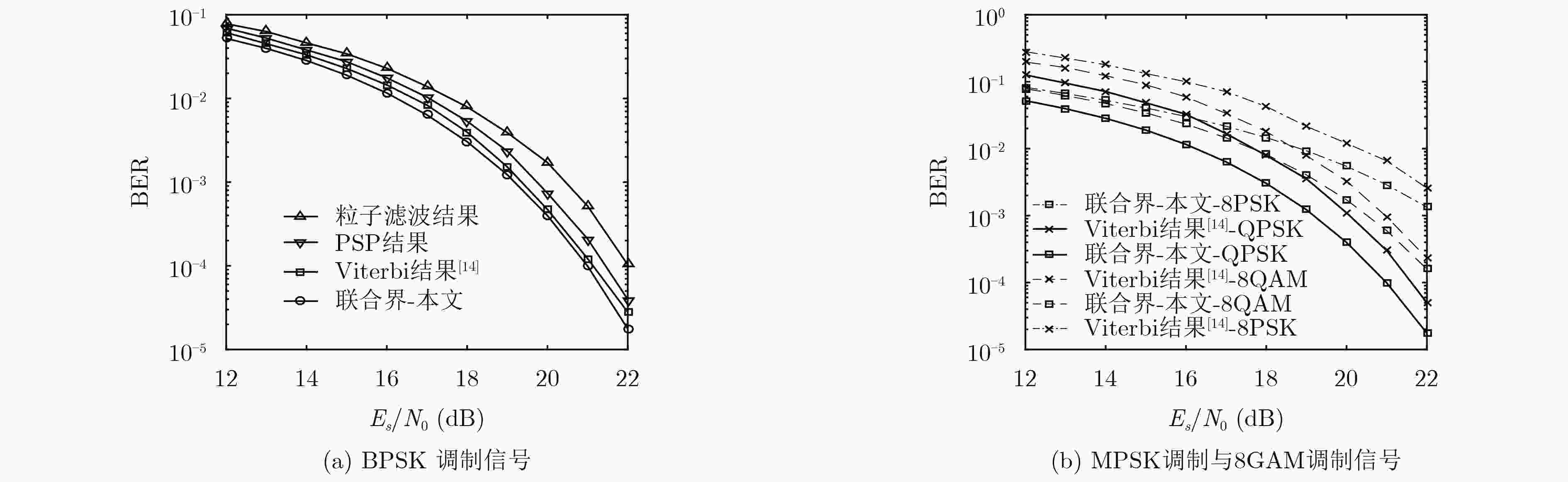
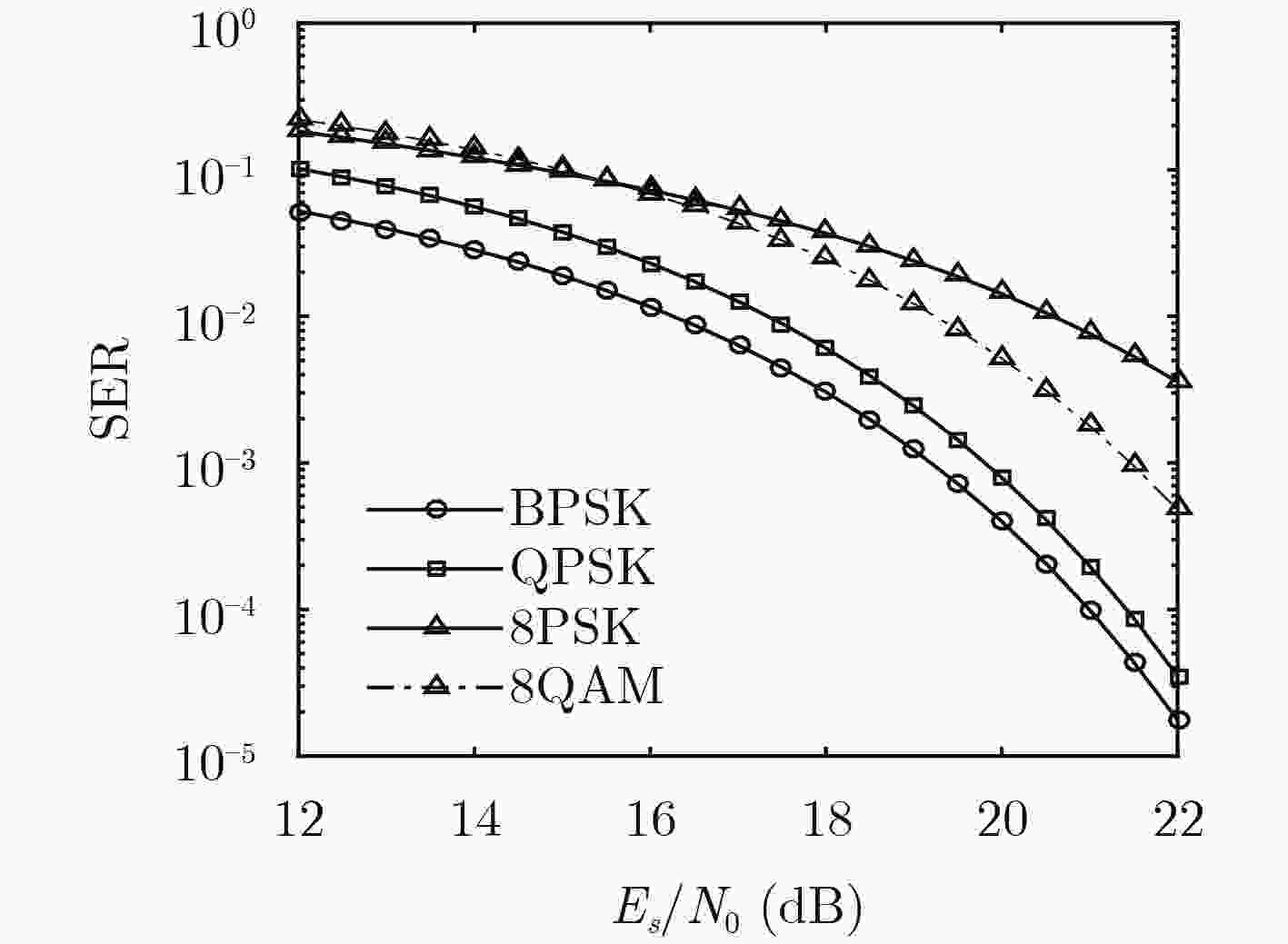
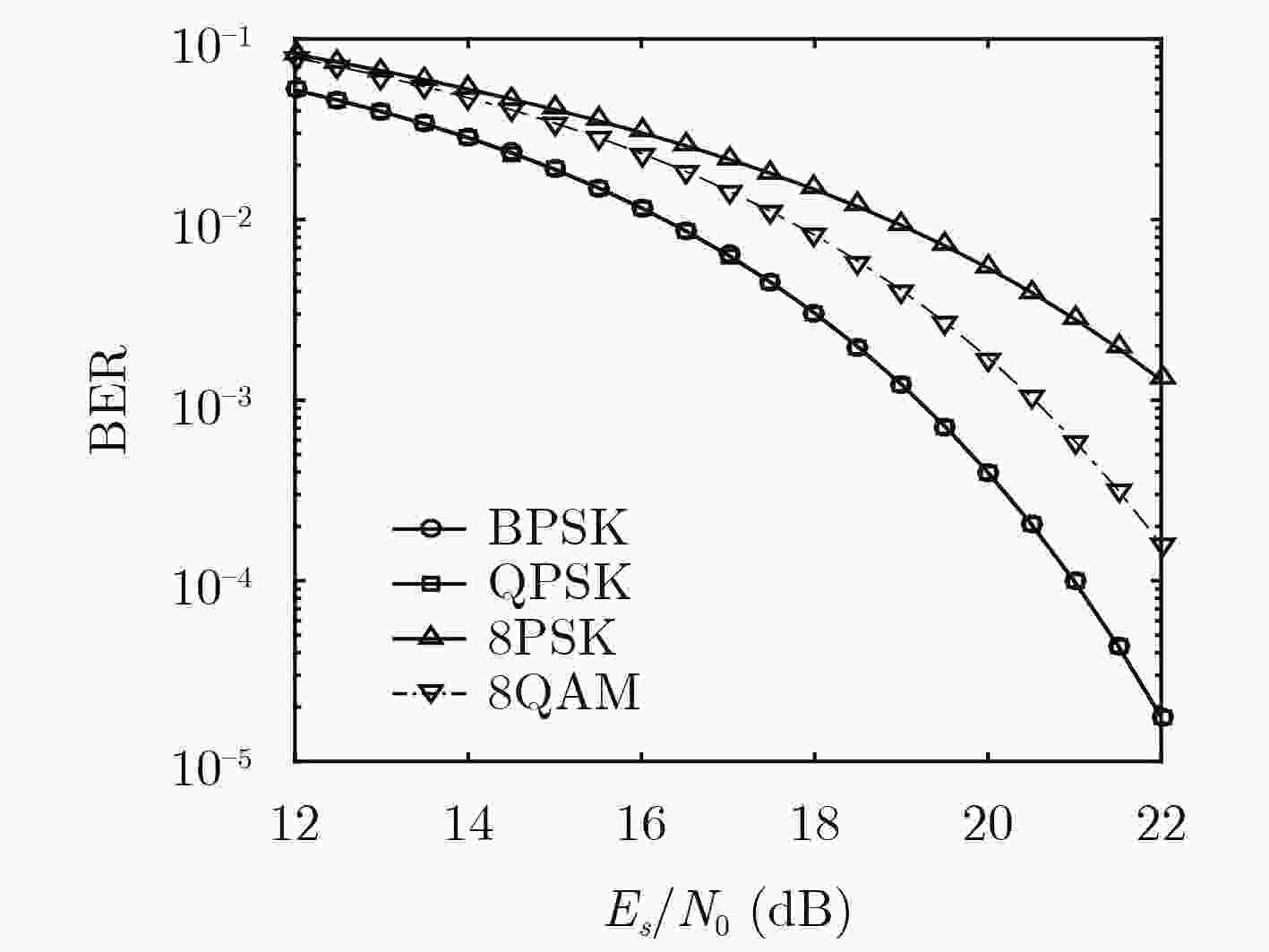
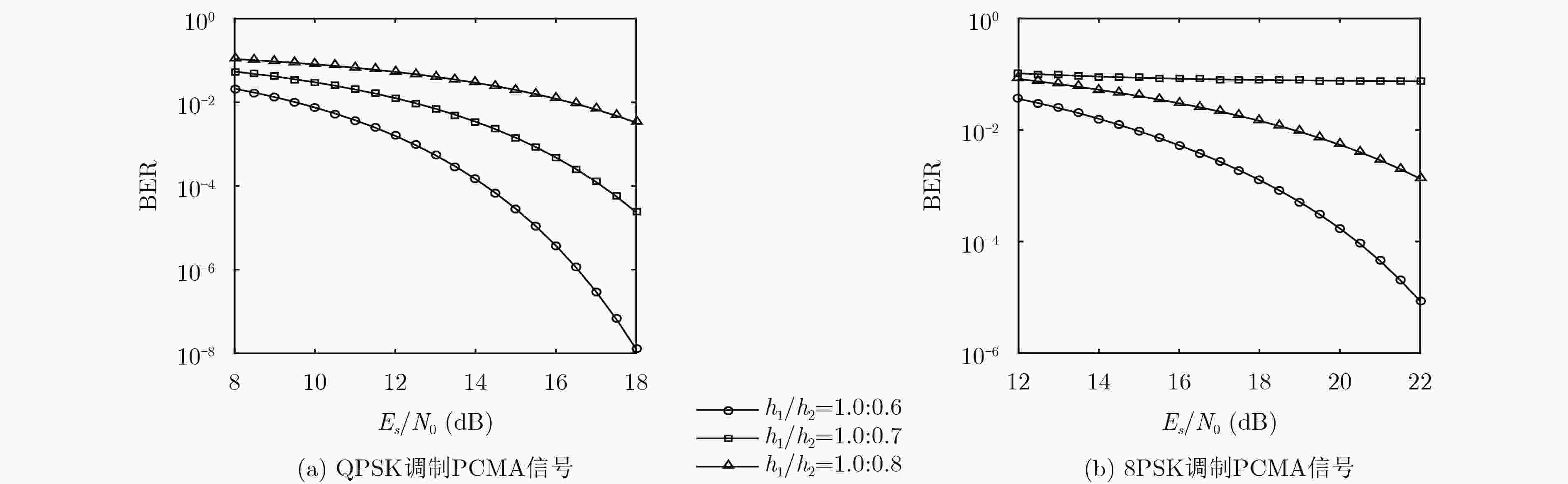
成对载波多址复用(PCMA)混合信号单通道盲分离性能界是衡量混合信号可分离程度以及分离算法性能的标准。针对PCMA混合信号,从发送信号模型出发构造调制信号比特与符号的空间映射,利用最大似然准则推导与混合信号分离算法无关的分离性能下界表达式,数值计算结果与理想情况下Viterbi仿真结果吻合,验证了所推导性能界的合理性。
Abstract:Blind separation performance bound of Paired Carrier Multiple Access (PCMA) mixed signal is a measure of the separability of mixed signals and the performance of the separation algorithm. For the PCMA mixed signal, the spatial mapping of the modulation signal bits and symbols is constructed from the transmit signal model. The maximum likelihood criterion is used to derive the lower bound expression of separation performance independent of the separation algorithm. Numerical results agree well with the Viterbi simulation results under ideal conditions, which verify the rationality of the derived performance boundaries.
-
DANKBERG M. Paired carrier multiple access for satellite communication[C]. Pacific Telecommunications Conference, Hawaii, USA, 1998: 10–20. HEIDARI S and NIKIAS C I. Co-channel interference mitigation in the time-scale domain: The CIMTS algorithm[J]. IEEE Transactions on Signal Processing, 1996, 44(9): 2151–2162. doi: 10.1109/78.536673 BRANDT-PEARCE M. Signal separation using fractional sampling in multiuser communications[J]. IEEE Transactions on Communications, 2000, 48(2): 242–251. doi: 10.1109/26.823557 TU Shilong, CHEN Shaohe, ZHENG Hui, et al. Particle filtering based signal-channel blind separation of co-frequency MPSK signals[C]. ISPACS 07, Xiamen, China, 2007: 89–92. TU Shilong, ZHENG Hui, and GU Na. Single-channel blind separation of two QPSK signals using per-survivor processing[C]. APCCAS 08, Macao, China, 2008: 473–476. CUI Penghui, JIANG Hua, CAO Kai, et al. The DFF-PSP iterative separation and theoretical bound for PCMA with long memory[J]. Chinese Journal of Electronics, 2016, 25(5): 880–885. doi: 10.1049/cje.2016.08.046 YANG Yong, PENG Hua, ZHANG Dongling, et al. Markov chain Monte Carlo-based separation of paired carrier multiple access signals[J]. IEEE Communications Letters, 2016, 20(11): 2209–2212. doi: 10.1109/LCOMM.2016.2599874 WU Chuanlong, ZHENG Liu, WANG Xiang, et al. Single-channel blind source separation of co-frequency overlapped GMSK signals under constant-modulus constraints[J]. IEEE Communications Letters, 2016, 20(3): 486–489. doi: 10.1109/LCOMM.2016.2521737 LIU Xiaobei, GUAN Yongliang, and KOH S N. Single-channel blind separation of co-frequency MPSK signals based on PSP algorithm with DFSE[C]. IEEE Military Communications Conference (MILCOM), Tampa, USA, 2015: 1509–1514. 廖灿辉, 万坚, 周世东. 两同频调制信号混合单通道盲分离的性能界[J]. 清华大学学报(自然科学版), 2010, 50(10): 1646–1650. doi: 10.16511/j.cnki.qhdxxb.2010.10.007LIAO Canhui, WAN Jian, and ZHOU Shidong. Single-channel blind separation performance bound of two co-frequency modulated signals[J]. Journal of Tsinghua University (Science and Technology) , 2010, 50(10): 1646–1650. doi: 10.16511/j.cnki.qhdxxb.2010.10.007 DUAN Chaowei, ZHAN Yafeng, and LIANG Hao. More general performance evaluation for single-channel PCMA signals blind separation[J]. IET Communications, 2017, 11(15): 2297–2302. doi: 10.1049/iet-com.2016.1445 PAN Baijun and TU Shilong. Blind separation of two QPSK signals based on lattice reduction[C]. 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 2017: 21–23. LEE P. Computation of the bit error rate of coherent M-ary PSK with gray code bit mapping[J]. IEEE Transactions on Communications, 1986, 34(5): 488–491. 万坚, 涂世龙, 廖灿辉, 等. 通信混合信号盲分离理论与技术[M]. 北京: 国防工业出版社, 2012.WAN Jian, TU Shilong, LIAO Canhui, et al. Theory and Technology on Blind Source Separation of Communication Signals[M]. Beijing: National Defense Industry Press, 2012. -





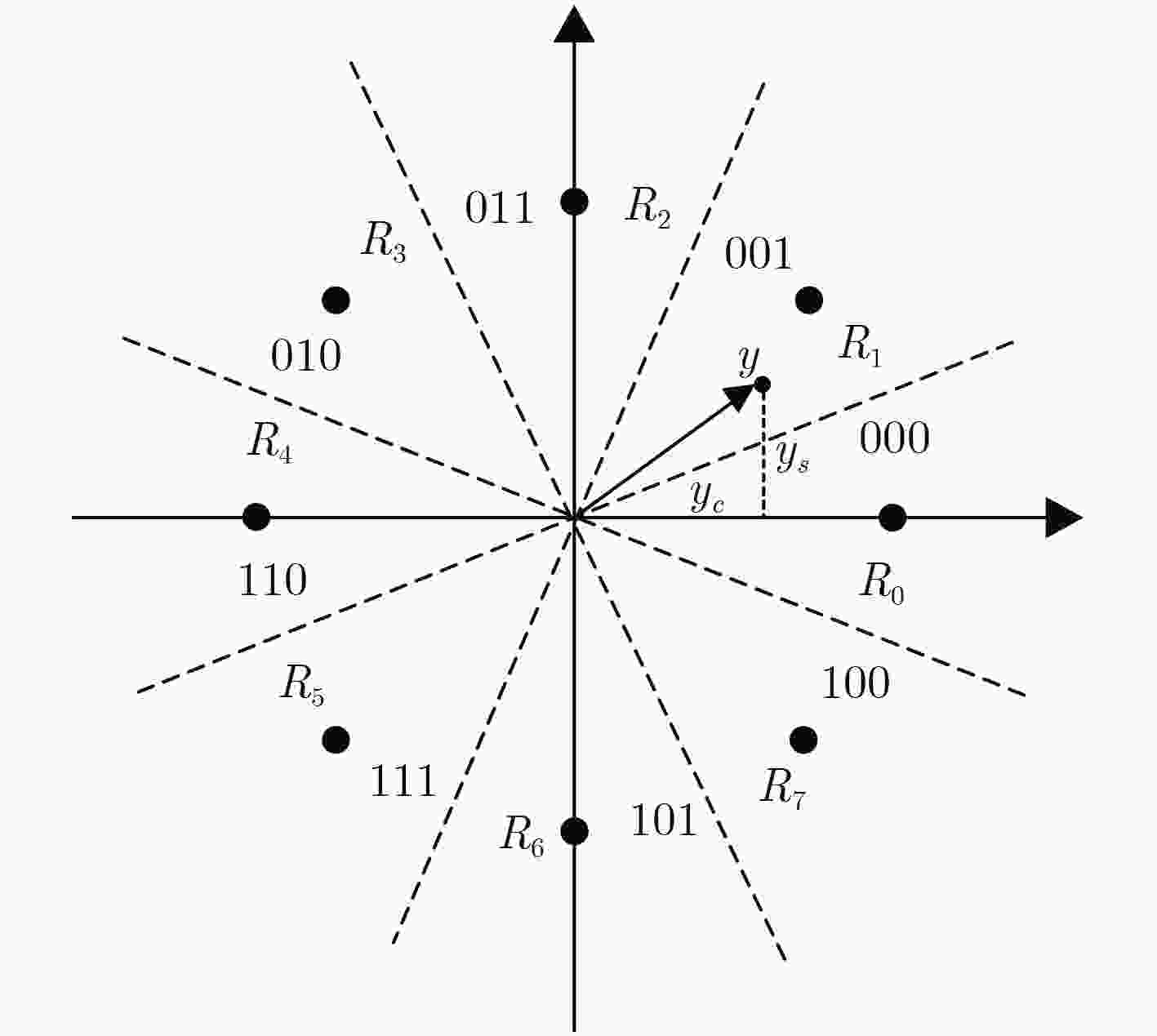
 下载:
下载:
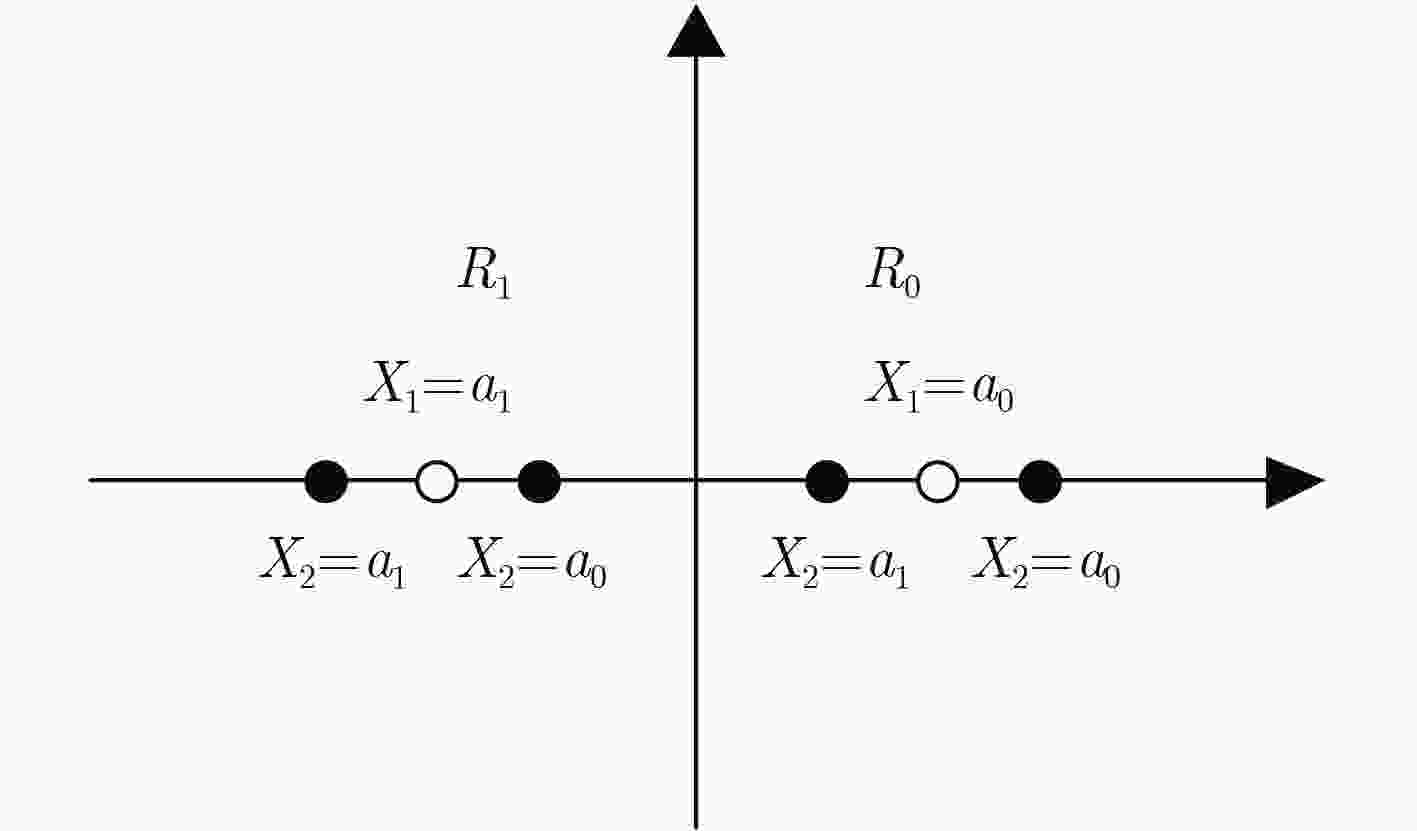
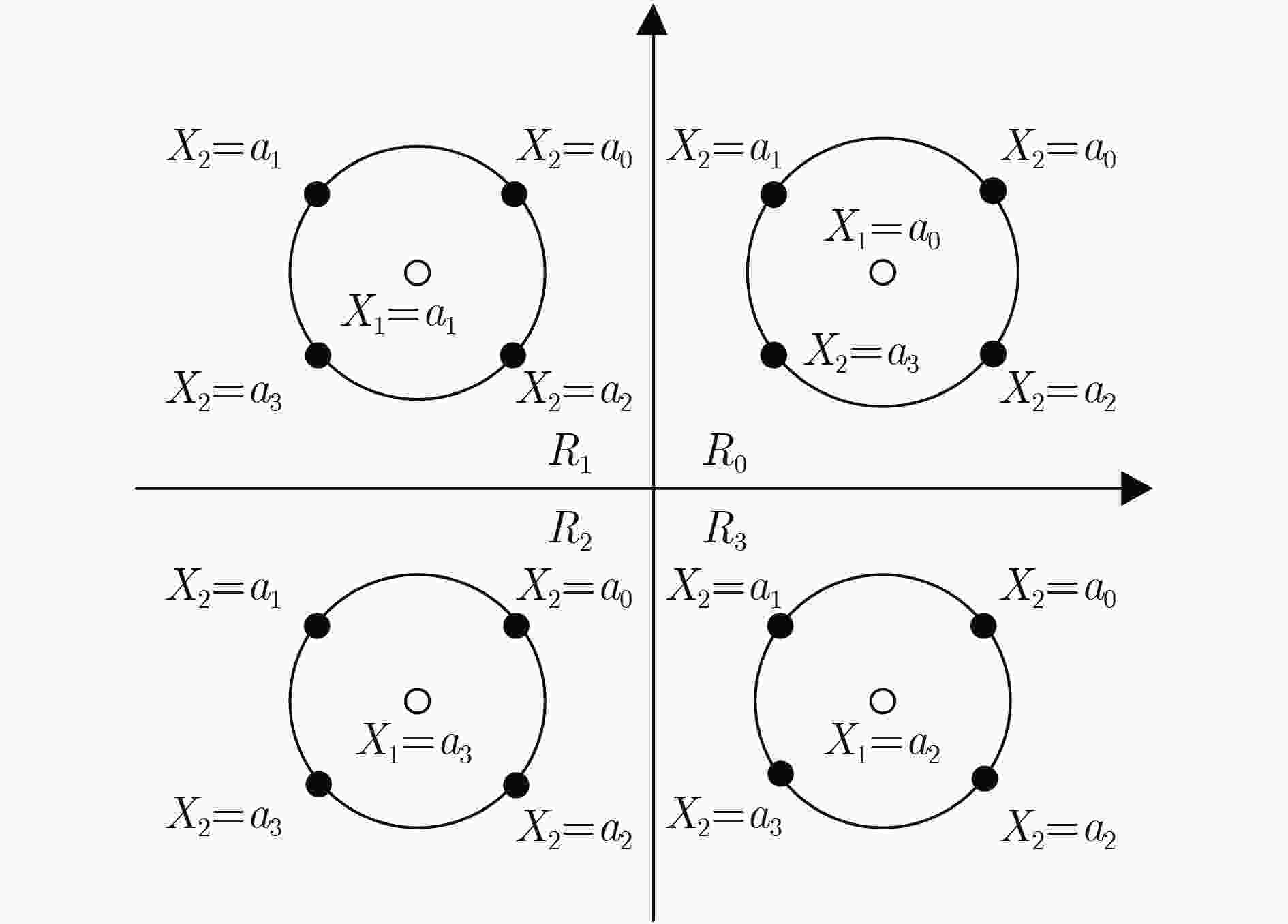
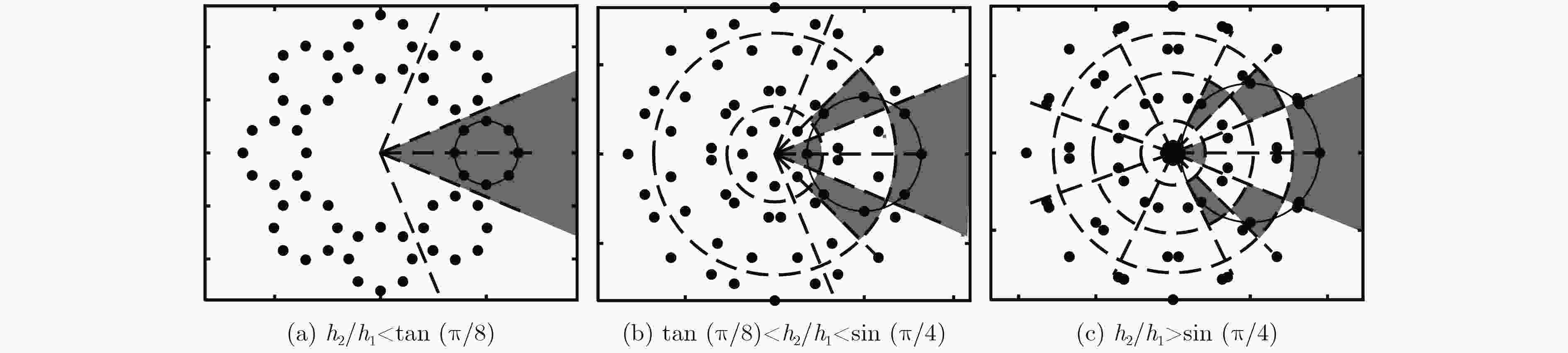




 下载:
下载:
