Cat Swarm Optimization Task Scheduling Algorithm Based on Double Arbitration Mechanism and Taguchi Orthogonal Method
-
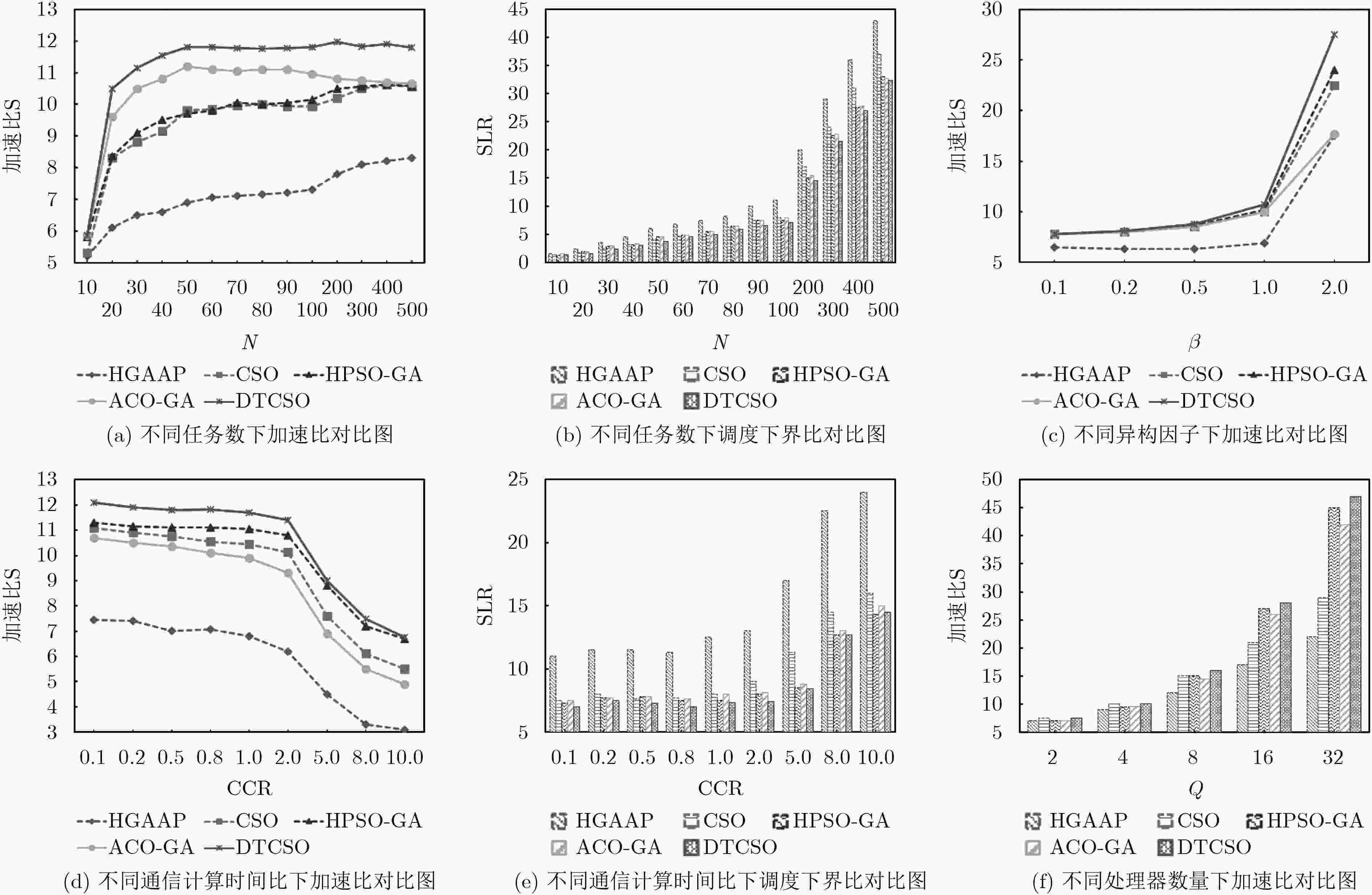
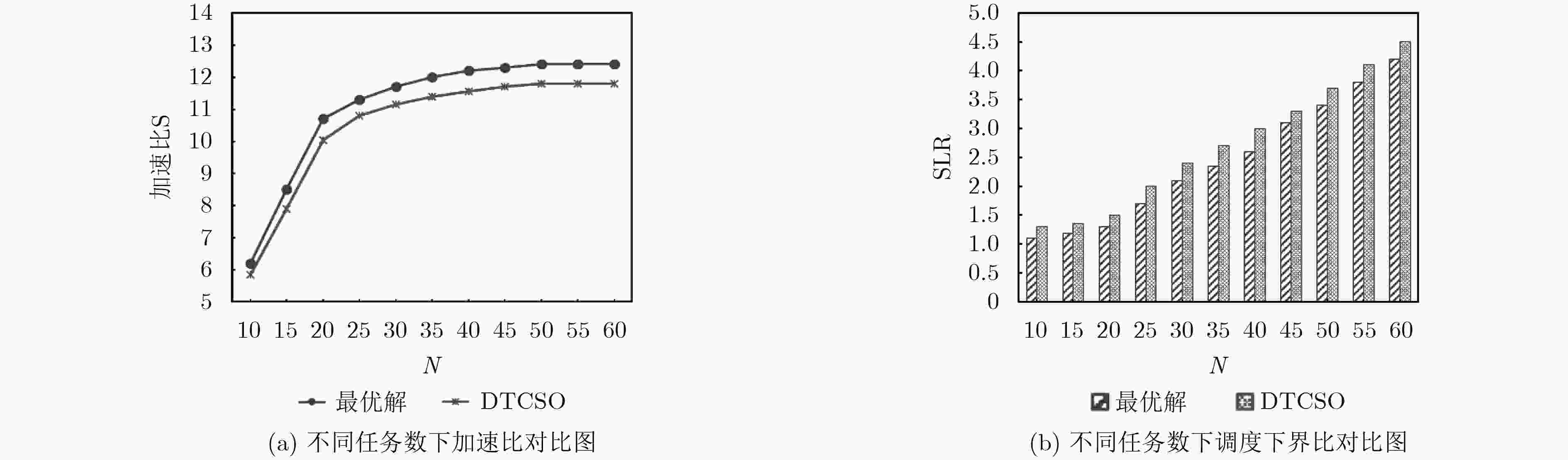
摘要: 针对异构计算系统任务调度过程中通信冲突以及算法运行时间的问题,该文提出一种基于双仲裁机制和田口正交法的猫群优化任务调度算法。首先利用双仲裁机制对任务资源进行管理,动态判决任务的分配,有效避免通信冲突,再将田口正交法应用到猫群优化过程的跟踪模式中,降低算法运行时间,提高解的质量。实验结果表明,该算法运行速度明显高于其他算法至少约10%,算法在处理大量任务时的并行化效果最优,在异构环境中也体现出其相当大的优势。Abstract: To solve communication conflicts and algorithm running time problem in task scheduling process of heterogeneous computing system, a cat swarm optimization task scheduling algorithm is proposed based on double arbitration mechanism and Taguchi orthogonal method. Firstly, the double arbitration mechanism is used to manage the task resources, and the task assignment is dynamically decided to avoid effectively communication conflicts. Then, the Taguchi orthogonal method is applied to the tracking mode of the cat swarm optimization process to reduce the algorithm running time and improve the quality of the solution. Experimental results show that the algorithm runs at a rate of at least about 10% faster than other algorithms. The algorithm performs best in parallelism when dealing with a large number of tasks and has considerable advantages in heterogeneous environments.
-
表 1 双仲裁映射判决算法
算法1 双仲裁映射判决算法 输入:TA, PLA, t, Tm 输出:有效的任务映射结果DAM(T) (1) if (( ${T_m} \cdot {t_a} \le t \le {T_m} \cdot {t_s}$) and ( ${T_m} \cdot s = {\rm IDLE}\parallel {\rm WAIT}$)) then
enQueue (Q, Tm)(2) Select Tm from Q where ${T_m} \cdot p$ is the highest (3) if (PLA=NULL) then (4) temp P·taskid $ \leftarrow {T_n} \cdot \rm{taskid}$;
temp P·pos $ \leftarrow {[(0},{0),(}{T_n} \cdot w,{T_n} \cdot h{)]}$;(5) ${T_n} \cdot s \leftarrow {\rm EXE}$;TA [i+1][0] $ \leftarrow {T_n} \cdot w$; TA [i+1][1] $ \leftarrow {T_n} \cdot h$; (6) insert node tempP into PLA; else (7) DAM(Tj, d); end if (8) end if 表 2 L8(27)正交阵列
实验序列号 考虑的因子 A B C D E F G 1 1 0 0 1 1 0 0 2 1 1 1 0 0 0 0 3 0 0 1 0 1 1 0 4 0 1 0 0 1 0 1 5 1 1 1 1 1 1 1 6 1 0 0 0 0 1 1 7 0 0 1 1 0 0 1 8 0 1 0 1 0 1 0 表 3 预估计算时间矩阵
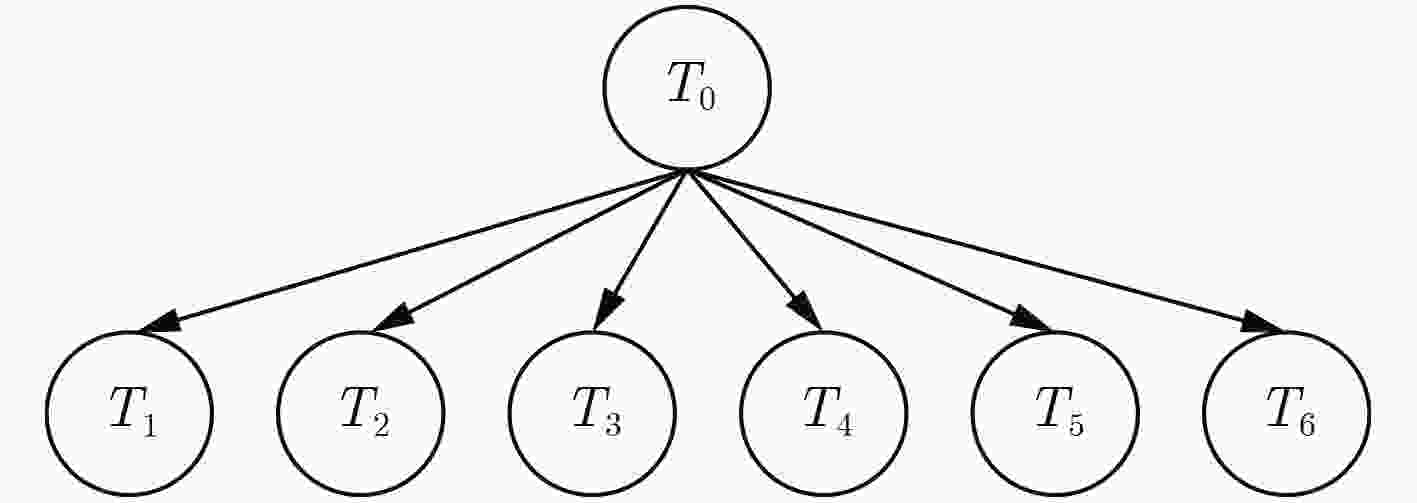
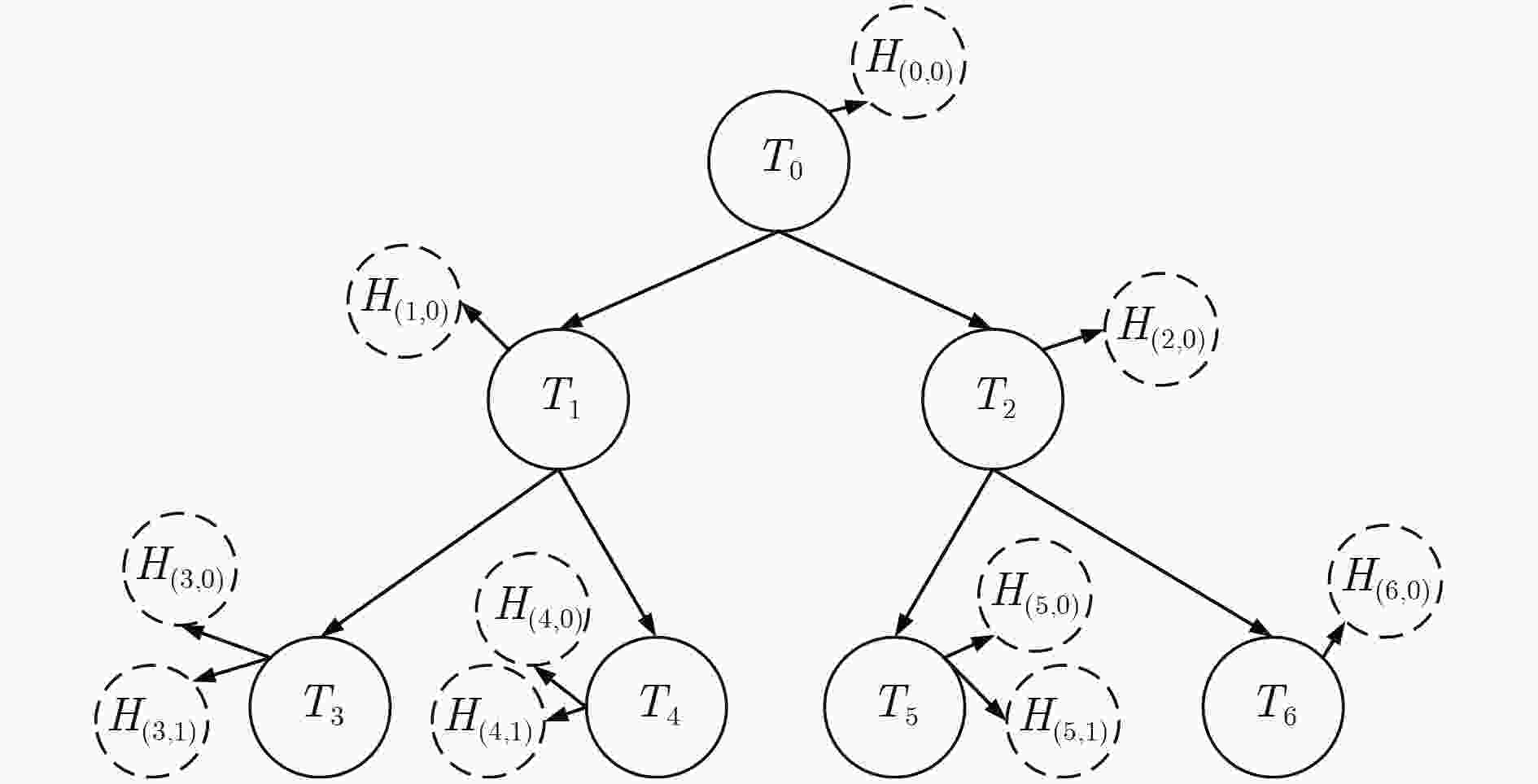
T0 T1 T2 T3 T4 T5 T6 P0 T0/P0 T1/P0 T2/P0 T3/P0 T4/P0 T5/P0 T6/P0 P1 T0/P1 T1/P1 T2/P1 T3/P1 T4/P1 T5/P1 T6/P1 P2 T0/P2 T1/P2 T2/P2 T3/P2 T4/P2 T5/P2 T6/P2 P3 T0/P3 T1/P3 T2/P3 T3/P3 T4/P3 T5/P3 T6/P3 P4 T0/P4 T1/P4 T2/P4 T3/P4 T4/P4 T5/P4 T6/P4 P5 T0/P5 T1/P5 T2/P5 T3/P5 T4/P5 T5/P5 T6/P5 P6 T0/P6 T1/P6 T2/P6 T3/P6 T4/P6 T5/P6 T6/P6 P7 T0/P7 T1/P7 T2/P7 T3/P7 T4/P7 T5/P7 T6/P7 表 4 田口-猫群优化算法
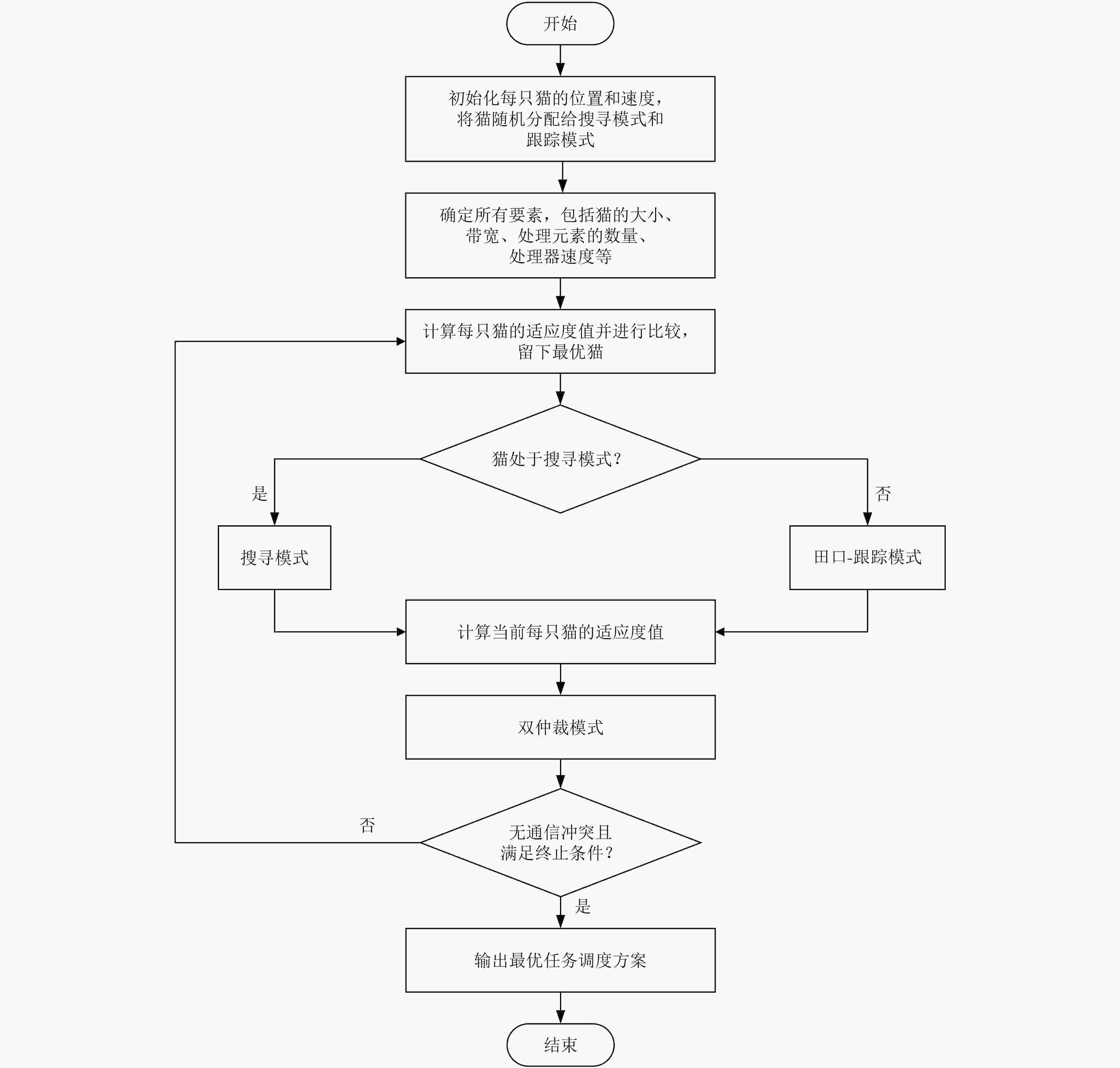
算法2 田口-猫群优化算法 输入:猫的初始位置,初始速度,MR, SMP, SRD, CDC, SPC
输出:最优的任务调度结果(1) if (seeking flag← 1) //按照搜寻模式进行 (2) 生成第k只猫的y (y=SMP) 份副本Zqd (1 ≤ q ≤ Y, 1 ≤ d ≤ D) ; //D是解空间的维数 (3) 每当CDC对Zqd进行加或减的变异操作就随机改变猫的维度, 确定被改变的猫的适应度; (4) 从Y中随机选取候选值后发现并替换猫的最佳位置;else (5) 选取两级田口正交阵列 ${L_n}{(}{{2}^{n - {1}}}{),}\forall n \ge N + {1}$; //N表示任务数量 (6) 根据式(2)生成两组速度并根据任务数量N确定任务调度的维数; (7) 根据正交阵列 ${L_n}{(}{{2}^{n - {1}}}{)}$计算n次实验的适应度值; (8) end if 选取当前最优个体 ${x_l}$和最佳位置 ${x_p}$; (9) if ( ${x_l} > {x_g}$) ${x_l} = {x_g}$; ${x_p} = {G_b}$; //当前最佳位置即全局最佳位置 (10) 根据式(4),式(5)计算并更新当前速度和位置; (11) if (达到最终条件) 输出最佳的任务调度顺序; (12) else 重新计算每只猫的适应度值;end if (13) end if 表 5 DTCSO算法参数设置
参数 值 猫的数量 100 最大迭代次数 1000 权重w 0.5 c1 1 r1 [0,1] MR 0.5 SMP 3 N {10,20,30,40,50,60,70,80,90,100,200,300,400,500} den {0.2,0.5,0.8} fat {0.1,0.4,0.8} reg {0.2,0.5,0.8} jump {1,2,4} CCR {0.1,0.2,0.5,0.8,1.0,2.0,5.0,8.0,10.0} $\beta $ {0.1,0.2,0.5,1.0,2.0} Q {2,4,8,16,32} 表 6 调度算法优良比较(%)
HGAAP CSO HPSO-GA ACO-GA DTCSO算法 更好 100 98.6 93.62 86.7 相同 0 0 0.08 0.6 更差 0 1.4 6.3 12.7 -
KHOKHAR A A, PRASANNA V K, SHAABAN M E, et al. Heterogeneous computing: Challenges and opportunities[J].Computer, 1993, 26(6): 18–27 doi: 10.1109/2.214439 朱晓敏, 贺川, 王建江,等. 异构计算系统中弹性节能调度策略研究[J]. 计算机学报, 2012, 35(6): 1313–1326 doi: 10.3724/SP.J.1016.2012.01313ZHU Xiaomin, HE Chuan, WANG Jianjiang, et al. An elastic energy-aware scheduling strategy for heterogeneous computing systems[J]. Journal of Computer, 2012, 35(6): 1313–1326 doi: 10.3724/SP.J.1016.2012.01313 MACHOVEC D, PASRICHA S, MACIELEWSKI A A, et al. Preemptive resource management for dynamically arriving tasks in an oversubscribed heterogeneous computing system[C]. IEEE, Parallel and Distributed Processing Symposium Workshops, Lake Buena Vista, USA, 2017: 54–64. DAOUD M I and KHARMA N. A hybrid heuristic-genetic algorithm for task scheduling in heterogeneous processor networks[J]. Journal of Parallel&Distributed Computing, 2011, 71(11): 1518–1531 doi: 10.1016/j.jpdc.2011.05.005 DING Shan, WU Jinhui, XIE Guoqi, et al. A hybrid heuristic-genetic algorithm with adaptive parameters for static task scheduling in heterogeneous computing system[C]. The 14th IEEE International Conference on Embedded Software And Systems, Sydney, Australia, 2017: 761–766. MORTEZA M and HADI S S. An efficient ACO-based algorithm for scheduling tasks onto dynamically reconfigurable hardware using TSP-likened construction graph[J]. Applied Intelligence, 2016, 45(3): 695–712 doi: 10.1007/s10489-016-0782-2 JING Chao. Ant-colony optimization based algorithm for energy-efficient scheduling on dynamically reconfigurable systems[C]. The Ninth IEEE International Conference on Frontier of Computer Science and Technology, Sydney, Australia, 2015: 127–134. KIANPISHEH S, CHARKARI N M, and KARGAHI M. Ant colony based constrained workflow scheduling for heterogeneous computing systems[J]. Cluster Computing, 2016, 19(3): 1–18 doi: 10.1007/s10586-016-0575-8 KUMAR N and VIDVARTHI D P. A novel hybrid PSO–GA meta-heuristic for scheduling of DAG with communication on multiprocessor systems[J]. Engineering with Computers, 2016, 32(1): 35–47 doi: 10.1007/s00366-015-0396-z WANG Hui, WU Zhij, RAHNAMAVAN S, et al. Enhancing particle swarm optimization using generalized opposition-based learning[J]. Information Sciences, 2011, 181(20): 4699–4714 doi: 10.1016/j.ins.2011.03.016 KUMAR Y and SAHOO G. An improved cat swarm optimization algorithm based on opposition-based learning and Cauchy operator for clustering[J]. Journal of Information Processing Systems, 2017, 13(4): 1000–1013 doi: 10.3745/JIPS.02.0022 JIANG Yunlian, SUN Guangzhong, WU Wentao, et al. Efficient communication contention aware scheduling in heterogeneous system[J]. Journal of University of Science&Technology of China, 2006, 8(8): 875–881 doi: 10.3969/j.issn.0253-2778.2006.08.015 BEAUMONT O, BOUDET V, and ROBERT Y. A realistic model and an efficient heuristic for scheduling with heterogeneous processors[C]. Proceeding 16th International Parallel and Distributed Processing Symposium, Ft.Lauderdale, USA, 2002: 1–14. WANG Yan, LI Kenli, and LI Keqin. Partition scheduling on heterogeneous multicore processors for multi-dimensional loops applications[J]. International Journal of Parallel Programming, 2016, 45(4): 1–26 doi: 10.1007/s10766-016-0445-2 LE D V, GO B S, SONG M G, et al. Mathematical design of a pulsed power induction coilgun system using the taguchi method[C]. IEEE 21st International Conference on Pulsed Power (PPC), Brighton, UK, 2017: 1–5. TSAI J T, FANG J C, and CHOU J H. Optimized task scheduling and resource allocation on cloud computing environment using improved differential evolution algorithm[J]. Computers&Operations Research, 2013, 40(12): 3045–3055 doi: 10.1016/j.cor.2013.06.012 SAMARAWEERA L, THALAGALA S, GAMAGE P, et al. Optimization of green sand casting parameters using taguchi method to improve the surface quality of white cast iron grinding plates—A case study[C]. IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 2017: 1723–1727. KUMAR B, KALRA M, and SINGH P. Discrete binary cat swarm optimization for scheduling workflow applications in cloud systems[C]. IEEE International Conference on Computational Intelligence & Communication Technology, Ghaziabad, India, 2017: 1–6. GABI D, ISMAIL A S, ZAINAL A, et al. Cloud scalable multi-objective task scheduling algorithm for cloud computing using cat swarm optimization and simulated annealing[C]. International Conference on Information Technology, Amman, Jordan, 2017: 1007–1012. SUTER F and HUNOLD D S. A synthetic task graph generator[OL]. https://github.com/frs69wq/daggen.2017.4. TOPCUOGLU H, HARIRI S, and WU Minyou. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Transactions on Parallel and Distributed Systems, 2002, 13(3): 260–274 doi: 10.1109/71.993206 ARABNELAD H and BARBOSA J G. List scheduling algorithm for heterogeneous systems by an optimistic cost table[J]. IEEE Transactions on Parallel&Distributed Systems, 2014, 25(3): 682–694 doi: 10.1109/TPDS.2013.57 -





 下载:
下载:


 下载:
下载:
