Scheduling Service Staffs for Alien Airlines Using Block Gibbs Sampling
-
摘要: 航空公司外航服务人员排班旨在优化员工排班方案以满足外航航班的人员资质需求,并最小化员工总工作时长和兼顾工作时间均衡,其本质是一个面向多任务类型、员工层次资质、白夜班轮换等约束的人员排班问题。现有算法未考虑白夜班轮换强制性约束,制约了它们的应用。为此,该文提出基于Block Gibbs的航空公司外航服务人员排班算法。算法首先设计了数据拷贝技巧以快速建模具有白夜晚班约束的排班问题,然后提出基于Block Gibbs的多员工有放回抽样优化策略。理论分析表明该文算法与基准算法具有同规模的计算复杂度,但却具有更高的抽样效率以加大可行解生成规模和求解速度。与此同时,在国内某大型航空公司外航服务部排班数据集上的实验表明:相比于基准算法,算法在工作总时长、有效工作时长、有效工作时长比例等指标上提升至少0.62%。Abstract: Scheduling staffs servicing alien airlines aims to yield task-person assignments by covering the required skills and minimizing employee total working hours as well as balancing staffs’ workload. Its essence is a personnel scheduling problem constrained by multiple task types, hierarchical skills as well as day and night alternation. The existing algorithms do not consider the constraint of day and night alternation. An algorithm is proposed to address that issue. The proposed algorithm firstly designs a data copy trick to quickly model the issue of staff scheduling constrained by day and night alternation. A novel Block Gibbs sampling technique with replacement is designed to efficiently optimize the formulated problem. Theoretical analysis indicates that the computational complexity of the proposed algorithm is the same scale to that of the baselines, whereas the proposed algorithm gains high sampling efficiency. Experimental results on a real dataset shows the improvement of the proposed algorithm over the existing methods is at least 0.62% in terms of evaluation measures.
-
Key words:
- Aircraft ground handling /
- Staff scheduling /
- Block Gibbs sampling /
- Hierarchical skill
-
表 1 算法1:基于Block Gibbs的航空公司外航服务人员排班算法
输入:任务集 ${{{Ω}}}$;员工资质集 ${{{P}} }$;折中因子 $\lambda $;迭代次数 $L$;
退火温度 $T\;$;衰减因子 $\beta $; block大小 $K$输出:航班-员工分配 $\left\{ {x_{ij}^d} \right\}$ (1) 采用第2.2节数据拷贝技巧构造辅助任务集 ${{{Ω}}}'$ (2) 利用第2.4节算法2产生松弛初始解 $\left\{ {x_{ij}^d} \right\}$ (3) for ${\rm{iter}} = 1,2, ·\!·\!· ,L$ (4) for $d = 1,2, ·\!·\!· ,M$ (5) 设 $\forall i,j,\quad x_{ij}^d = 0$以移除员工 $d$任务分配集 (6) 抽样员工 $d$白夜班属性 ${y^d}{\rm{ \sim Berp}}({N_0}/N)$
// ${N_0},N$表示任务集中白天航班数和总航班数(7) foreach task ${l_{ij}} \in {{{Ω}}} \cup {{{Ω}}}'$ (8) if (式(5)或式(6)不满足) then $x_{ij}^d = 1,{y^d} = {t_{ij}}$
//确认员工d的白夜班类型 ${y^d}$(9) else $x_{ij}^d{\rm{ \sim }}\Pr ( \cdot |{x^{ - d}},x_{ - ij}^d,y) \propto {\rm{boolean \ of\ eqn(5)}}$
$/ {\rm{value\ of\ eqn}}(1)$ //抽样员工航班分配(10) ${{{U}} } = \left\{ {d|{x^d_{ij}} = 1,d = 1,2, ·\!·\!· ,M} \right\}$,
${{{{U}} }^{{{\rm c}} }} = \left\{ {d|x_{ij}^d = 0,{y^d} = {t_{ij}}} \right\}$(11) ${{{{K}} }^{{{\rm c}} }} = {{{{U}} }^{{\rm c} }}\left( {{\rm{randperm}}(|{{{{U}} }^{{{\rm c}} }}|,K{\rm{)}}} \right)$, $\forall d \in {{K}^{\rm c}} $,
$x_{ij}^d = 1$, //向某一航班增加 $ K $名员工(12) ${{{KU}} } = {{{{K}} }^{{{\rm c}} }} \cup {{{U}} }\left( {{\rm{randperm}}(|{{{{K}} }^{{{\rm c}} }} \cup {{{U}} }|,K{\rm{)}}} \right)$
//向某一航班抽回 $K$名员工(13) ${{{{x}}}^{\rm{new}}}{\rm{ \sim }}\Pr (x_{ij}^{d\,\!'} = 0,d\,\!' \in K{{{U}} }|{x^{ - d\,\!'}},y) $
$\propto {\rm{boolean \ of \ eqn(5)}}/{\rm{value \ of \ eqn}}(1)$(14) 采用模拟退火算法控制可行解 ${{{{x}} }^{\rm new}}$的接受或拒绝 (15) $T = T \times \beta $ 表 2 算法2:基于Block Gibbs的初始解优化算法
输入:任务集 ${{{Ω}}}$;员工资质集 ${{{P}} }$;迭代次数 $L$;退火温度 $T\,$;衰
减因子 $\beta $; block大小 $K$输出:航班-员工分配 $\left\{ {x_{ij}^d} \right\}$ (1) 初始化 ${y^1},{y^2}, ·\!·\!· ,{y^M} = 0$ (2) for ${\rm{iter}} = 1,2, ·\!·\!· ,L$ (3) for $d = 1,2, ·\!·\!· ,M$ (4) 设 $\forall i,j,\quad x_{ij}^d = 0$以移除员工 $d$任务分配集 (5) 抽样员工 $d$白夜班属性 $({\rm{new}}{y^d},{{\rm new}}{{{{x}} }^d}) \sim $
$ \Pr ({y^d},x_{ij}^d = I[{y^d} = = {t_{ij}}]|{y^{ - d}},{{{x}} }) \propto {\rm{ value \ of \ eqn (7)}}$(6) if $\left ({\rm eqn}(7) {等于}\sum {{{{{γ}}}_{ij}}(t)} \right)$ return $\left\{ {x_{ij}^d} \right\}$
// 得到满足约束的松弛解(7) 采用模拟退火算法控制可行解 ${{\rm new}}{{{{x}} }^d}$的接受或拒绝 (8) ${{{U}} } = \left\{ {h|{y_d} = {y_h},h = 1,2, ·\!·\!· ,M} \right\}$,
${{{{U}}}^{\rm c}} = \left\{ {h|{y_d} \ne {y_h},h = 1,2, ·\!·\!· ,M} \right\}$(9) ${{{{K}} }^{{{\rm c}} }} = {{{{U}} }^{{{\rm c}} }}\left( {{\rm randperm}(|{{{{U}} }^{{{\rm c}} }}|,K{\rm{)}}} \right)$ (10) ${{{KU}} } \!=\! {{{{K}} }^{{{\rm c}} }} \!\cup\! {{{U}} }\left( {{\rm randperm}(|{{{{K}} }^{{{\rm c}} }} \!\cup\! {{{U}} }|,K{\rm{)}}} \right)$
$ \propto $ value of eqn(7)(11) ${{\rm new}}{{{{x}} }^d} = \left( {\left( {{{{{U}}}^{\rm c}} \cup {{{U}} }} \right)\backslash {{{{K}}}U}} \right) \cup \left\{ {{y_h} = {y_i}|h \in {{{{K}} }U}} \right\}$ (12) 采用模拟退火算法控制可行解 ${{\rm new}}{{{{x}} }^d}$的接受或拒绝 (13) $T = T \times \beta $ 表 3 计算复杂度对比
算法 计算复杂度 本文算法 $O \left(L \times N \times \left(M \times K + \max |{\gamma ^k}|\right)\right)$ Optimizing staff scheduling by Monte-Carlo simulation[13] $O \left(L \times N \times M \times \max |{\gamma ^k}|\right)$ Constraint staff scheduling using monte carlo tree search[14] $O \left(L \times N \times M\lg M \times \max |{\gamma ^k}|\right)$ A simulation approach for re-assigning of personnel[15] $O\left(L \times N \times M \times \max |{\gamma ^k}|\right)$ 表 4 与基于Monte Carlo的基准算法对比可行解生成效率
算法 抽样次数 可行解生成规模 本文算法 $L\! \times\! M \!\times\! \left( {2N + 1} \right)$ $\prod\limits_{d = 1}^M {\prod\limits_{i = 1}^{14} {\prod\limits_{j = 1,{t_{ij}} = {y^d}}^{{n_i}} {{{\left( {2 +\! C({M_d} - {M_{ij}},K) \times\! C({M_{ij}} + K,K)} \right)}^L}} } } $ Optimizing staff scheduling by Monte-Carlo simulation[13] $L \!\times\! M \!\times\! N$ ${2^{L \times N \times M}}$ Constraint staff scheduling using monte carlo tree search[14] $L \!\times\! M \!\times\! N$ ${2^{L \times N \times M}}$ 表 5 航班计划表数据示例
星期 航班号 白/夜班 到岗时间 起飞时间 组长数 控制员工数 普通员工数 1 PK852 1 5:30 8:15 1 3 2 1 J2067 1 5:30 6:30 0 1 0 1 SU205 1 8:00 11:39 1 3 5 1 JS152 1 8:45 12:00 0 3 0 表 6 员工资质信息表数据示例
姓名 KE SU GA PK J2 IR 7C VN JS LH 李仁骥 0 3 3 3 3 3 0 3 3 1 黄芳 0 2 2 2 2 2 0 2 2 1 张华冰 0 2 2 2 2 2 0 2 2 1 孔清钺 0 2 2 2 2 2 0 2 2 2 李健 0 1 1 1 1 1 0 1 1 1 表 7 实验对比
算法 WH (h) EH (h) EP (%) WB MA 60.6 53.5 90.8 185.9 BP 46.2 44.1 96.6 141.2 MC 50.1 47.5 94.8 155.8 MCTS 48.7 46.4 96.7 146.7 BG ( $\lambda $=0.05) 45.3 43.7 97.3 145.5 表 8 折中因子
${λ}$ 影响算法 WH (h) EH (h) EP (%) WB RT (s) BG ( $\lambda $=0) 45.1 43.1 96.7 424.6 20.9 BG ( $\lambda $=0.05) 45.3 43.7 97.3 145.5 18.7 BG ( $\lambda $=0.40) 45.6 43.9 97.1 137.7 18.2 BG ( $\lambda $=0.80) 45.6 44.0 97.2 131.5 24.8 BG ( $\lambda $=1.00) 45.6 43.9 97.0 131.5 24.2 表 9 模拟退火温度T 影响分析
T WH (h) EH (h) EP (%) WB RT (s) 0 45.77 42.77 96.53 473.51 27.66 50 44.97 43.29 97.17 439.60 27.12 100 44.97 42.95 97.12 422.26 26.24 500 44.99 42.97 96.37 427.88 27.27 1000 44.94 42.92 96.38 380.80 25.51 表 10 温度衰减因子
$\beta $ 影响分析${\rm{\beta }}$ WH (h) EH (h) EP (%) WB RT (s) 0.70 44.90 43.19 96.85 403.86 26.50 0.80 44.98 42.60 96.02 417.24 27.47 0.90 45.00 43.15 96.78 429.66 25.61 0.95 45.01 42.78 96.00 442.08 28.30 0.99 44.92 43.58 97.31 389.05 26.94 -
BERGH J, BELIËN J, and BRUECKER P. Personnel scheduling: A literature review[J].European Journal of Operational Research, 2013, 226(3): 367–385 doi: 10.1016/j.ejor.2012.11.029 ERNST A T, JIANG H, and KRISHNAMOORTHY M. Staff scheduling and rostering: A review of applications, methods and models[J]. European Journal of Operational Research, 2004, 153(1): 3–27 doi: 10.1016/S0377-2217(03)00095-X KHOSRAVI A K, TAMANNAEI T, and REISI-NAFCHI M. A comprehensive approach for railway crew scheduling problem[J]. International Journal of Transportation Engineering, 2017, 4(3): 197–210 doi: 10.22119/IJTE.2017.43836 RAHIMIAN E, AKARTUNALI K, and LEVINE J. A hybrid integer and constraint programming approach to solve nurse rostering problems[J]. Computers&Operations Research, 2017, 82: 83–94 doi: 10.1016/j.cor.2017.01.016 FUJITA K, MURAKAMI K, and AMASAKA K. A shift scheduling model introducing non-regular employees for hotel restaurants[J]. Journal of Japanese Operations Management and Strategy, 2016, 6(1): 17–33 doi: 10.20586/joms.6.1_17 BRUECKER P D and BURKE E. Personnel scheduling: Models and complexity[J]. European Journal of Operational Research, 2011, 210(3): 467–473 doi: 10.1016/j.ejor.2010.11.017 RESTREPO M I, ENDRON B, and ROUSSAUB M. A two-stage stochastic programming approach for multi-activity tour scheduling[J]. European Journal of Operational Research, 2017, 262(2): 620–635 doi: 10.1016/j.ejor.2017.04.055 WALTER M and ZIMMERMANN J. Minimizing average project team size given multi-skilled workers with heterogeneous skill levels[J]. Computers&Operations Research, 2016, 70: 163–179 doi: 10.1016/j.cor.2015.11.011 BRUECKER P, BERGH J, BELIËN J, et al. Workforce planning incorporating skills: state of the art[J]. European Journal of Operational Research, 2015, 243(1): 1–16 doi: 10.1016/j.ejor.2014.10.038 FIRAT M, BRISKORN D, and LAUGIER A. A Branch-and-Price algorithm for stable workforce assignments with hierarchical skills[J]. European Journal of Operational Research, 2016, 251(2): 676–685 doi: 10.1016/j.ejor.2015.11.039 SMET P, BILGINL B, DE CAUSMAECKER P, et al. Modelling and evaluation issues in nurse rostering[J]. Annals of Operations Research, 2014, 218(1): 303–326 doi: 10.1007/s10479-012-1116-3 SCIPIONE D, SULLIVAN F, ZAVADSKY V, et al. Optimizing staff scheduling by Monte-Carlo simulation[C]. Proceedings of the Annual Symposium on Computer Application in Medical Care, Washington D.C, USA, 1992: 678–681. CHENG C C, CARVE N, and RAHIMI S. Constraint based staff scheduling optimization: Using single player Monte Carlo tree search[C]. Proceedings of the 16th International Conference on Artificial Intelligence, Las Vegas, USA, 2014: 633–638. ZULCH G, ROTTINGER S, and VOLLSTED T. A simulation approach for planning and re-assigning of personnel in manufacturing[J]. International Journal of Production Economics, 2004, 90(2): 265–277 doi: 10.1016/j.ijpe.2003.11.008 GÉRARD M, CLAUTIAUX F, and SADYKOV R. Column generation based approaches for a tour scheduling problem with a multi-skill heterogeneous workforce[J]. European Journal of Operational Research, 2016, 252(3): 1019–1030 doi: 10.1016/j.ejor.2016.01.036 -





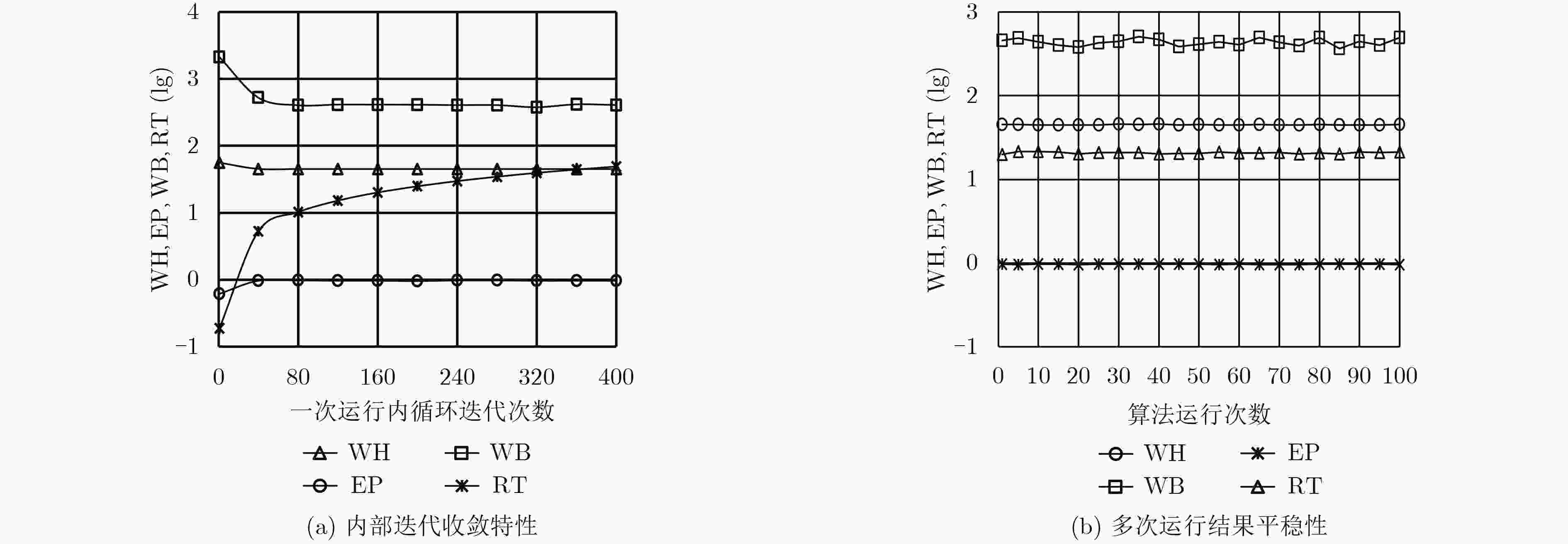
 下载:
下载:




 下载:
下载:
