High Throughput Dual-mode Reconfigurable Floating-point FFT Processor
-
摘要: 高吞吐浮点可灵活重构的快速傅里叶变换(FFT)处理器可满足尖端雷达实时成像和高精度科学计算等多种应用需求。与定点FFT相比,浮点运算复杂度更高,使得浮点型FFT的运算吞吐率与其实现面积、功耗之间的矛盾问题尤为突出。鉴于此,为降低运算复杂度,首先将大点数FFT分解成若干个小点数基2k 级联子级实现,提出分别针对128/256/512/1024/2048点FFT的优化混合基算法。同时,结合所提出同时支持单通道单精度和双通道半精度两种浮点模式的新型融合加减与点乘运算单元,首次提出一款高吞吐率双模浮点可变点FFT处理器结构,并在28 nm标准CMOS工艺下进行设计并实现。实验结果表明,单通道单精度和双通道半精度浮点两种模式下的运算吞吐率和输出平均信号量化噪声比分别为3.478 GSample/s, 135 dB和6.957 GSample/s, 60 dB。归一化吞吐率面积比相比于现有其他浮点FFT实现可提高约12倍。Abstract: In the advanced applications of real-time radar imaging and high-precision scientific computing systems, the design of high throughput and reconfigurable Floating-Point (FP) FFT accelerator is significant. Achieving high throughput FP FFT with low area and power cost poses a greater challenge due to high complexity of FP operations in comparison to fixed-point implementations. To address these issues, a serial of mixed-radix algorithms for 128/256/512/1024/2048-point FFT are proposed by decomposing long FFT into short implementations with cascaded radix-2k stages so that the complexity of multiplications can be significantly reduced. Besides, two novel fused FP add-subtract and dot-product units for dual-mode functionality are proposed, which can either compute on a pair of double precision operands or on two pairs of single precision operands in parallel. Thus, a high throughput dual-mode floating-point variable length FFT is designed. The proposed processor is implemented based on SMIC 28 nm CMOS technology. Simulation results show that the throughput and Signal-to-Quantization Noise Ratio (SQNR) in single-channel single precision and dual-channel half precision floating-point mode are 3.478 GSample/s, 135 dB and 6.957 GSample/s, 60 dB respectively. Compare to the other FP FFT, this processor can achieve 12 times improvement of normalized throughput-area ratio.
-
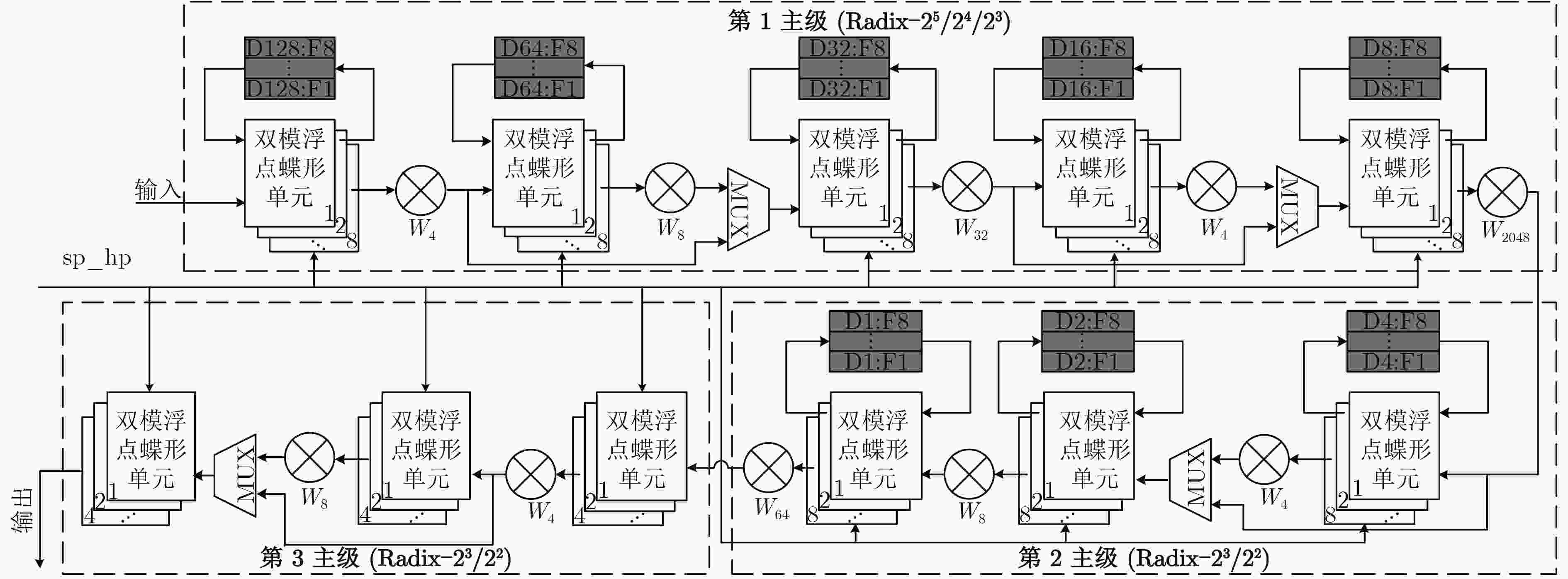
表 1 本文所提出的混合基算法
点数 优化算法 每个子级相应的基底 1 2 3 4 5 6 7 8 9 10 128 23-22-22 4 8 128 4 16 4 256 24-22-22 4 16 4 256 4 16 4 512 24-22-23 4 16 4 512 4 32 4 8 1024 25-22-23 4 8 32 4 1024 4 32 4 8 2048 25-23-23 4 8 32 4 2048 4 8 64 4 8 表 2 双模浮点融合加减运算单元关键路径
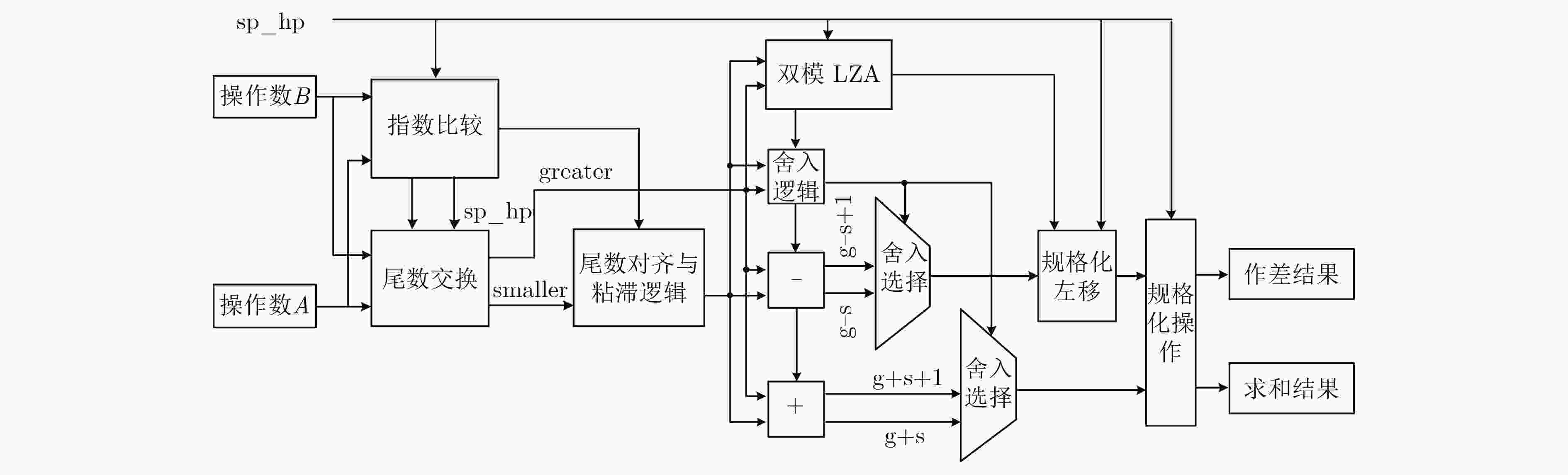
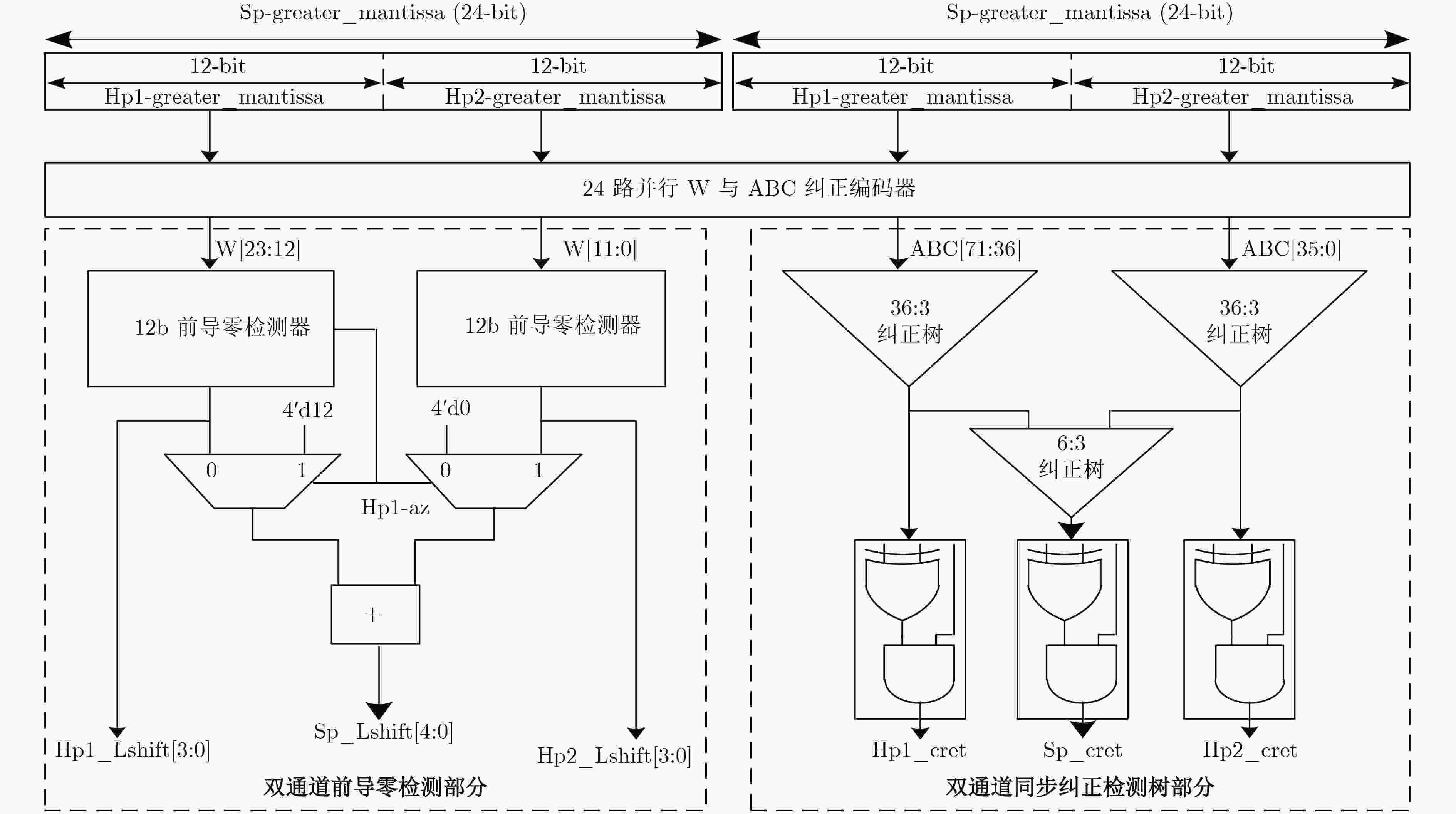
模块名 流水级 延时(ns) 数据提取与尾数生成 1 0.43 指数比较与尾数交换 1 0.77 指数阶差与尾数对齐 2 1.98 尾数求和差 3 1.47 LZA 3 0.35 规格化左移 3 0.16 表 3 双模浮点融合加减运算单元性能比较结果
参数 文献[6] 参考结构T1 本文 工艺 (nm) 45 28 28 归一化面积 (μm2) 5226 (100%) 2665 (51%) 2317 (44%) 工作频率 (MHz) 1920 500 435 计算延迟 (ns) 1.0 6.0 6.9 功耗 (mW) 5.2 0.6 0.4 功耗×周期 2.70 (100%) 1.20 (44%) 0.84 (31%) 表 4 双模浮点融合点乘运算单元关键路径
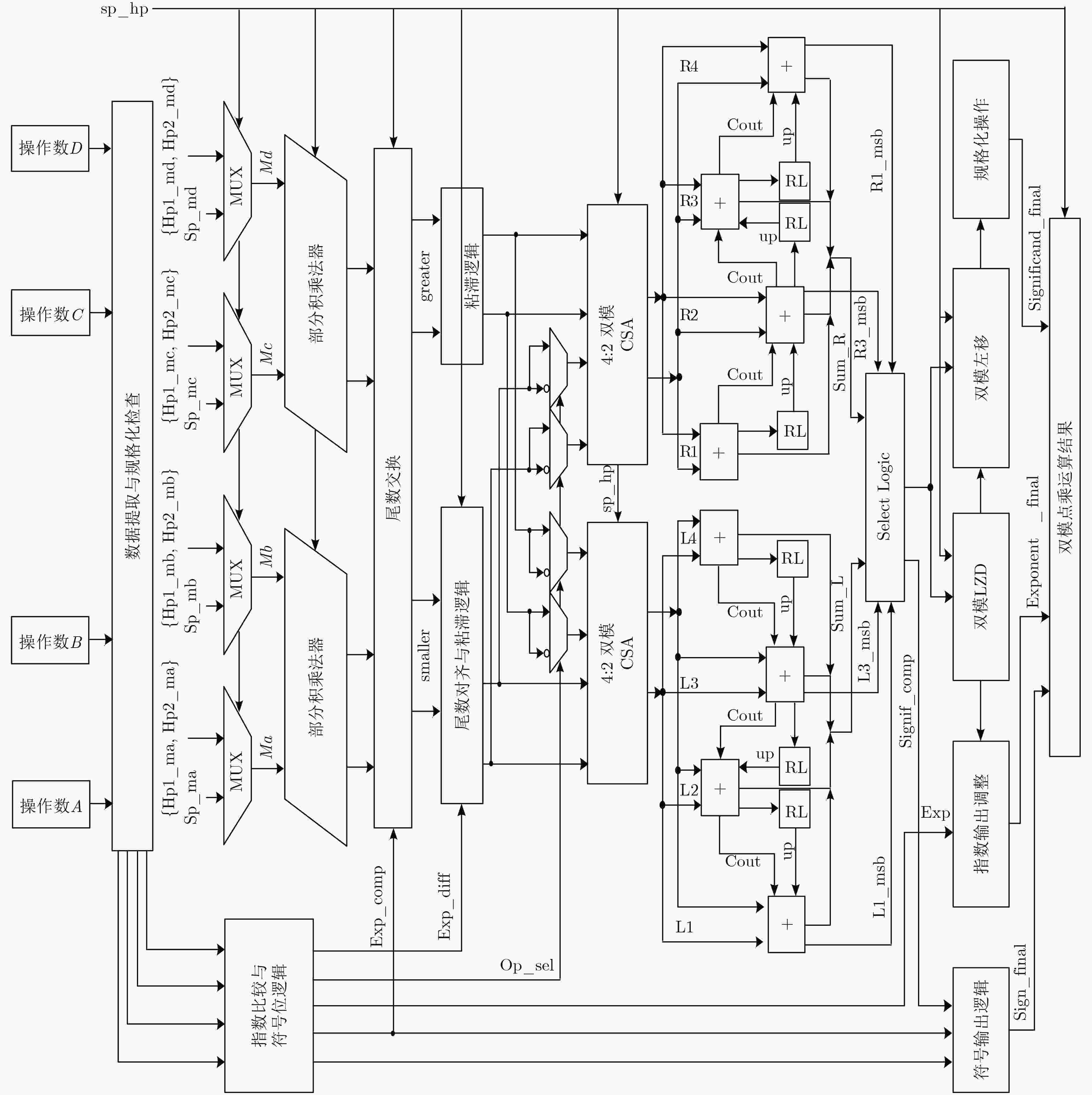
模块名 流水级 延时(ns) 数据提取与指数比较 1 0.33 尾数部分积相乘 1 0.87 指数阶差与乘积对齐 2 1.25 双模4:2 CSA 2 0.20 双加法舍入路径 2 0.53 LZD与规格化左移 3 1.98 表 5 双模浮点融合点乘运算单元性能比较结果
参数 文献[5] 参考结构T2 本文 工艺 (nm) 45 28 28 归一化面积 (μm2) 12865 (100%) 10336 (80%) 10701 (83%) 工作频率 (MHz) 1493 500 435 计算延迟 (ns) 2.1 6.0 6.9 功耗 (mW) 16.9 2.7 2.5 功耗×周期 11.3 (100%) 5.3 (47%) 5.6 (50%) 表 6 双模浮点FFT整体性能对比
性能参数 文献[2] 文献[9] 文献[16] 本文 工艺 (nm) 90 65 55 28 FFT结构 基于存储器 Hybrid MDF MDF FFT点数 512 1024 1024 128/256/512/1024/2048 并行度 8 1 1 8 数据类型:字长 (bit) 块浮点:12 浮点:32 定点:16 浮点:32/浮点:16 平均输出SQNR (dB) 57 139 55 SP:135/HP:60 时钟频率 (MHz) 324 400 200 435 计算时间 (μs) 0.3 2.6 5.1 0.2/0.3/0.6/1.1/2.2 运算吞吐率 (MSample/s) 2592 400 200 SP:3478/HP:6957 平均功耗 (mW) 42 417 8 104 @435 MHz 有效面积 (mm2) 0.93 1.19 0.15 1.41 归一化面积 10.0 22.1 1.9 16.0 归一化吞吐率面积比 259 18 103 SP:220/HP:440 -
吕倩, 苏涛. 基于改进型快速双线性参数估计的复杂运动目标ISAR成像[J]. 电子与信息学报, 2016, 38(9): 2301–2308 doi: 10.11999/JEIT151359LÜ Qian and SU Tao. ISAR imaging of targets with complex motion based on the modified fast bilinear parameter estimation[J]. Journal of Electronics&Information Technology, 2016, 38(9): 2301–2308 doi: 10.11999/JEIT151359 HUANG Shenjui and CHEN S. A high-throughput radix-16 FFT processor with parallel and normal input/output ordering for IEEE 802.15.3c systems[J]. IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers, 2012, 59(8): 1752–1765 doi: 10.1109/TCSI.2011.2180430 LAN G and FRANK H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Boston: Artech House Publishers, 2005: 154–210. 陈杰男, 费超, 袁建生, 等. 超高速全并行快速傅里叶变换器[J]. 电子与信息学报, 2016, 38(9): 2410–2414 doi: 10.11999/JEIT160036CHEN Jienan, FEI Chao, YUAN Jiansheng, et al. An ultra-high-speed fully-parallel fast Fourier transform design[J]. Journal of Electronics&Information Technology, 2016, 38(9): 2410–2414 doi: 10.11999/JEIT160036 JONGWOOK S and EARL E. Improved architectures for a floating-point fused dot product unit[C]. IEEE Symposium on Computer Arithmetic, Austin, USA, 2013: 41–48. doi: 10.1109/ARITH.2013.26. JONGWOOK S and EARL E. Improved architectures for a fused floating-point add-subtract unit[J]. IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers, 2012, 59(10): 2285–2291 doi: 10.1109/TCSI.2012.2188955 CHO T and LEE H. A high-speed low-complexity modified radix-25 FFT processor for high rate WPAN applications[J]. IEEE Transactions on Very Large Scale Integration(VLSI)Systems, 2013, 21(1): 187–191 doi: 10.1109/TVLSI.2011.2182068 WANG Chao, YAN Yuwei, and FU Xiaoyu. A high-throughput low-complexity radix-24-22-23 FFT/IFFT processor with parallel and normal input/output order for IEEE 802.11ad systems[J]. IEEE Transactions on Very Large Scale Integration(VLSI)Systems, 2015, 23(11): 2728–2732 doi: 10.1109/TVLSI.2014.2365586 WANG Mingyu and LI Zhaolin. A hybrid SDC/SDF architecture for area and power minimization of floating-point FFT computations[C]. IEEE International Symposium on Circuits and Systems, Montreal, Canada, 2016: 2170–2173. doi: 10.1109/ISCAS.2016.7539011. EARL E and HANI H. FFT implementation with fused floating-point operations[J]. IEEE Transactions on Computers, 2012, 61(2): 284–288 doi: 10.1109/TC.2010.271 TANG S N, TSAI J W, and CHANG T Y. A 2.4-GS/s FFT processor for OFDM-based WPAN applications[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2010, 57(6): 451–455 doi: 10.1109/TCSII.2010.2048373 NIE Zedong, ZHANG Fengjuan, LI Jie, et al. Low-power digital ASIC for on-chip spectral analysis of low-frequency physiological signals[J]. Journal of Semiconductors, 2012, 33(6): 67–70 doi: 10.1088/1674-4926 IEEE 754-2008. IEEE Standard for Floating-Point Arithmetic[S]. 2008. doi: 10.1109/IEEESTD.2008.5976968. PETER K. Correcting the normalization shift of redundant binary representations[J]. IEEE Transactions on Computers, 2009, 58(10): 1453–1439 doi: 10.1109/TC.2009.38 YANG C H, YU T H, and DEJAN M. Power and area minimization of reconfigurable FFT processors: A 3GPP-LTE example[J]. IEEE Journal of Solid-State Circuits, 2011, 47(3): 757–768 doi: 10.1109/JSSC.2011.2176163 MARIO G, HUANG S J, CHEN S G, et al. The serial commutator FFT[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2016, 63(10): 974–978 doi: 10.1109/TCSII.2016.2538119 YANG K J, TSAI S H, and CHUANG G. MDC FFT/IFFT processor with variable length for MIMO-OFDM systems[J]. IEEE Transactions on Very Large Scale Integration(VLSI)Systems, 2013, 21(4): 720–731 doi: 10.1109/TVLSI.2012.2194315 -





 下载:
下载:



 下载:
下载:
