基于小波的稳健光流计算方法

王洪雁; 郑佳; 裴炳南

doi:10.11999/JEIT180077

基于小波的稳健光流计算方法

doi: 10.11999/JEIT180077

1.
大连大学辽宁省北斗高精度位置服务技术工程实验室大连 116622
2.
大连大学大连市环境感知与智能控制重点实验室大连 116622

基金项目: 国家自然科学基金(61301258, 61271379)，中国博士后科学基金(2016M590218)

详细信息

作者简介:
王洪雁：男，1979年生，副教授，博士，主要研究方向为MIMO雷达信号处理、毫米波通信、无人机控制

郑佳：男，1990年生，硕士生，研究方向为机器视觉、无人机容错控制

裴炳南：男，1956年生，教授，博士，博士生导师，主要研究方向为雷达信号处理、毫米波通信

通讯作者:
王洪雁　 gglongs@163.com

中图分类号: TN919.8
计量
- 文章访问数: 1409
- HTML全文浏览量: 465
- PDF下载量: 40
- 被引次数: 0
出版历程
- 收稿日期: 2018-01-19
- 修回日期: 2018-09-18
- 网络出版日期: 2018-09-21
- 刊出日期: 2018-12-01

A Robust Optical Flow Calculation Method Based on Wavelet

1.
Liaoning Engineering Laboratory of BeiDou High-precision Location Service, Dalian University, Dalian 116622, China
2.
Dalian Key Laboratory of Environmental Perception and Intelligent Control, Dalian University, Dalian 116622, China

Funds: The National Natural Science Foundation of China (61301258, 61271379), China Postdoctoral Science Foundation (2016M590218)

摘要

摘要: 针对系统误差导致光流计算稳健性较差及精度较低的问题，该文提出一种基于小波多分辨理论的稳健光流计算方法。所提算法基于小波多尺度分辨率特性，将光照条件变化及传感器噪声引起的系统误差包含进光流计算中以改善光流计算的稳健性及估计精度，并通过总体最小二乘法求解超定小波光流方程组以获得光流矢量。仿真结果表明，与传统的Lucas-Kanade算法、Horn-Schunck算法及基于小波的全向图像光流估计方法相比，所提算法可显著改善光流估计精度及稳健性。
- 光流计算 /
- 小波多分辨 /
- 系统误差 /
- 总体最小二乘
Abstract: Focusing on the issue that the systematic errors lead to poor robustness and low accuracy of optical flow calculation, a robust optical flow calculation method is proposed in this paper, which is based on the wavelet multi-resolution theory. With the multi-resolution characteristics of wavelet, the system error caused by variation of illumination conditions and sensor noise is incorporated into the calculation of optical flow to improve the robustness and estimation accuracy. In what follows, the total least square method is used to solve the over-determined wavelet optical flow equations to obtain the optical flow vector. As compared to the traditional Lucas-Kanade approach, Horn-Schunck method and optical flow estimation in omnidirectional images using wavelet approach, simulation results show that the proposed algorithm can significantly improve the accuracy of optical flow estimation and the robustness of the optical flow field.
- Optical flow calculation /
- Wavelet multi-resolution /
- System error /
- Total least squares

HTML全文

图 2 慢速运动场景下所得光流

下载: 全尺寸图片幻灯片

图 1 慢速运动场景下采集的连续4帧图像

下载: 全尺寸图片幻灯片

图 4 快速运动场景下所得光流

下载: 全尺寸图片幻灯片

图 3 快速运动场景下所采集的连续4帧图片

下载: 全尺寸图片幻灯片

图 5 不同运动场景下相邻2帧图像所得光流平均角度误差、平均角度标准差及绝对平均误差随迭代次数变化

下载: 全尺寸图片幻灯片

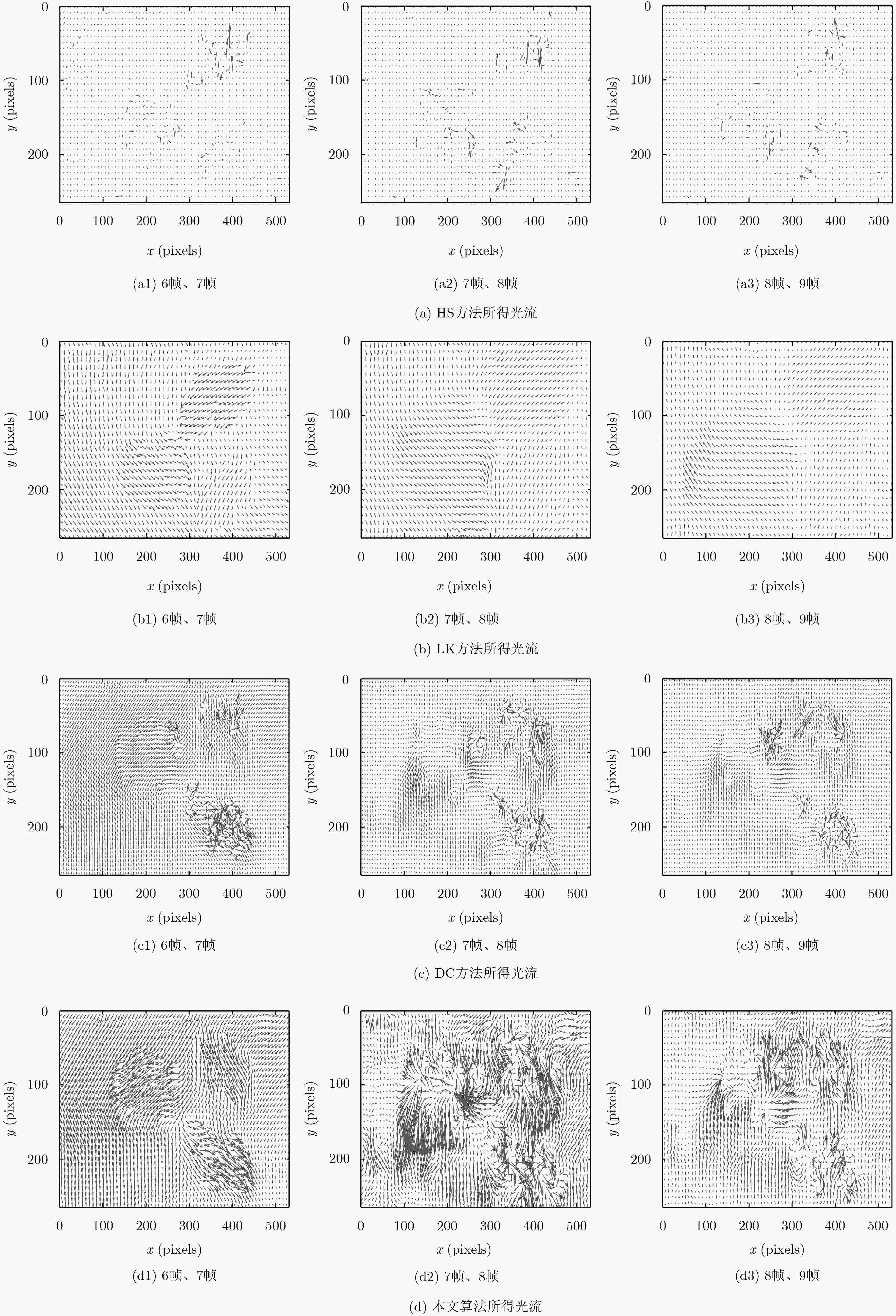
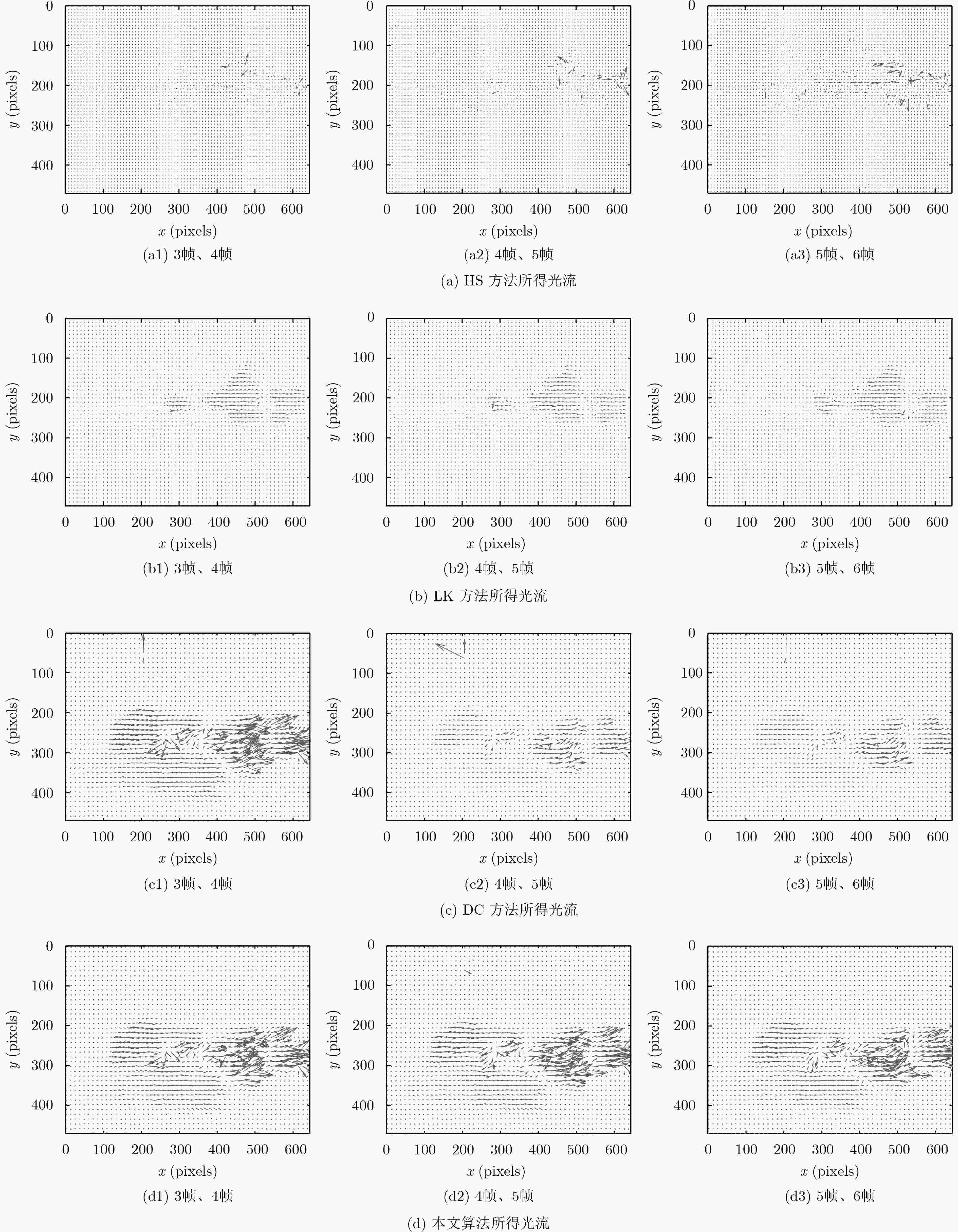
表 2 快速运动下光流性能参数

算法类型	E			F			H
算法类型	3帧、4帧	4帧、5帧	5帧、6帧	3帧、4帧	4帧、5帧	5帧、6帧	3帧、4帧	4帧、5帧	5帧、6帧
HS	12.23	12.20	12.27	12.59	12.54	12.57	0.91	0.93	0.90
LK	8.76	8.75	8.78	9.12	9.08	9.10	0.78	0.76	0.77
DC	4.89	4.78	4.82	4.35	4.33	4.36	0.34	0.36	0.35
本文算法	2.08	2.11	2.13	2.47	2.46	2.41	0.26	0.23	0.25

下载: 导出CSV

表 1 慢速运动下光流性能参数

算法类型	E			F			H
算法类型	6帧、7帧	7帧、8帧	8帧、9帧	6帧、7帧	7帧、8帧	8帧、9帧	6帧、7帧	7帧、8帧	8帧、9帧
HS	11.56	11.48	11.51	12.07	11.98	12.05	0.79	0.76	0.80
LK	7.64	7.57	7.60	8.39	8.36	8.38	0.68	0.64	0.67
DC	3.21	3.19	3.34	3.45	3.42	3.47	0.34	0.36	0.32
本文算法	1.95	1.89	1.94	2.26	2.23	2.25	0.18	0.16	0.17

下载: 导出CSV

表 3 求解光流所需时间(s)

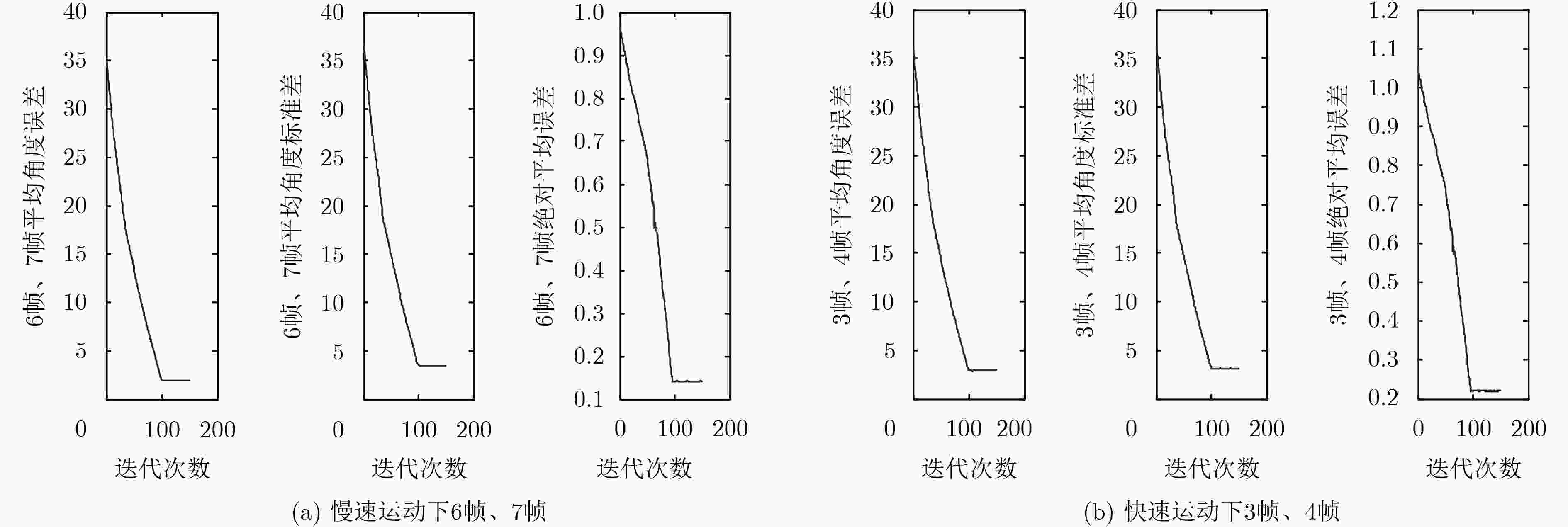
算法类型	慢速运动耗时			快速运动耗时
算法类型	6帧、7帧	7帧、8帧	8帧、9帧	3帧、4帧	4帧、5帧	5帧、6帧
HS光流法	4.42	4.38	4.45	5.58	5.39	5.45
LK光流法	4.14	4.03	4.18	4.67	4.31	4.46
DC光流法	3.23	3.19	3.42	3.53	3.42	3.47
本文算法	2.26	2.24	2.31	2.50	2.46	2.41

下载: 导出CSV

参考文献(22)

BLESER G and HENDEBY G. Using optical flow as lightweight SLAM alternative[C]. International Symposium on Mixed and Augmented Reality, Orlando, USA, 2009, 175–176. doi: 10.1109/ISMAR.2009.5336475.

ZHANG Congxuan, Ge Liyue, CHEN Zhen, et al. Guided filtering: Toward edge-preserving for optical flow[J]. IEEE Access, 2018, 6: 26958–26970 doi: 10.1109/ACCESS.2018.2831920

GOPPERT J, YANTEK S, and HWANG I. Invariant Kalman filter application to optical flow based visual odometry for UAVs[C]. IEEE Ninth International Conference on Ubiquitous and Future Networks, Milan, Italy, 2017: 99–104. doi: 10.1109/ICUFN.2017.7993755.

PASTOR-MORENO D, SHIN H S, and WALDOCK A. Optical flow localisation and appearance mapping (OFLAAM) for long-term navigation[C]. IEEE International Conference on Unmanned Aircraft Systems, Colorado, USA, 2015: 980–988. doi: 10.1109/ICUAS.2015.7152387.

CHAMORRO-MARTINEZ J and FERNANDEZ-VALDIVIA J. A new approach to motion pattern recognition and its application to optical flow estimation[J]. IEEE Transactions on Systems Man&Cybernetics Part C, 2006, 37(1): 39–51 doi: 10.1109/TSMCC.2006.876044

HORN B K P and SCHUNCK B G. Determining optical flow[J]. Artificial Intelligence, 1981, 17(1/3): 185–203 doi: 10.1016/0004-3702(81)90024-2

LUCAS B D and KANADE T. An iterative image registration technique with an application to stereo vision[C]. International Joint Conference on Artificial Intelligence, Vancouver, Canada, 1981: 674–679.

DRULEA M and NEDEVSCHI S. Total variation regularization of local-global optical flow[C]. IEEE International Conference on Intelligent Transportation Systems, Washington, DC, USA, 2011: 318–323. doi: 10.1109/ITSC.2011.6082986.

NIU Yan, XU Zhiwen, CHE Xiangjiu, et al. Dynamically removing false features in pyramidal lucas-kanade registration[J]. IEEE Transactions on Image Processing, 2014, 23(8): 3535–3544 doi: 10.1109/TIP.2014.2331140

田天, 周兵, 李波, 等. 基于解析小波的光流计算方法[J]. 北京航空航天大学学报, 2003, 29(6): 548–551 doi: 10.13700/j.bh.1001-5965.2003.06.019

TIAN Tian, ZHOU Bing, LI Bo, et al. Optical flow computation based on analytic wavelet[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(6): 548–551 doi: 10.13700/j.bh.1001-5965.2003.06.019

MAGAREY J and KINGSBURY N. Motion estimation using a complex-valued wavelet transform[J]. IEEE Transactions on Signal Processing, 2002, 46(4): 1069–1084 doi: 10.1109/78.668557

WU Yute, KANADE T, COHN J, et al. Optical flow estimation using wavelet motion model[C]. IEEE International Conference on Computer Vision, Bombay, India, 1998: 992–998. doi: 10.1109/ICCV.1998.710837.

项学智, 赵春晖. 形态梯度恒常的复值小波光流求解[J]. 哈尔滨工程大学学报, 2008, 29(8): 872–876 doi: 10.3969/j.issn.1006-7043.2008.08.020

XIANG Xuezhi and ZHAO Chunhui. An estimation of complex wavelet optical flow with invariant morphological gradient[J]. Journal of Harbin Engineering University, 2008, 29(8): 872–876 doi: 10.3969/j.issn.1006-7043.2008.08.020

DEMONCEAUX C and KACHI-AKKOUCHE D. Optical flow estimation in omnidirectional images using wavelet approach[C]. IEEE International Conference on Computer Vision and Pattern Recognition, Madison, USA, 2003: 71–76. doi: 10.1109/CVPRW.2003.10080.

SCHAFFRIN B and FELUS Y A. On the multivariate total least-squares approach to empirical coordinate transformations. Three algorithms[J]. Journal of Geodesy, 2008, 82(6): 373–383 doi: 10.1007/s00190-007-0186-5

NIAZ M T, IMDAD F, KIM S, et al. Total least-square-based receiver for asymmetrically clipped optical-orthogonal frequency divisional multiplexing visible light communication system[J]. IET Optoelectronics, 2017, 11(4): 129–133 doi: 10.1049/iet-opt.2015.0133

ARTYUSHENKO V M and VOLOVACH V I. The effect of multiplicative noise on probability density function of signal and additive noise[C]. IEEE Workshop on Electronic and Networking Technologies, Moscow, Russia, 2018: 1–5. doi: 10.1109/MWENT.2018.8337270.

DATESMAN A. Shot noise in radiobiological systems[J]. Journal of Environmental Radioactivity, 2016, 164: 365–368 doi: 10.1016/j.jenvrad.2016.06.017

CELLA G. Thermal noise correlations and subtraction[J]. Physics Letters A, 2017, 382: 2269–2274 doi: 10.1016/j.physleta.2017.06.026

SHOU Guofa, XIA Ling, JIANG Mingfeng, et al. Truncated total least squares: A new regularization method for the solution of ECG inverse problems[J]. IEEE Transactions on Bio-medical Engineering, 2008, 55(4): 1327–1335 doi: 10.1109/TBME.2007.912404

曲付勇, 孟祥伟. 基于约束总体最小二乘方法的到达时差到达频差无源定位算法[J]. 电子与信息学报, 2014, 36(5): 1075–1081 doi: 10.3724/SP.J.1146.2013.01019

QU Fuyong and MENG Xiangwei. Source localization using TDOA and FDOA measurements based on constrained total least squares algorithm[J]. Journal of Electronics&Information Technology, 2014, 36(5): 1075–1081 doi: 10.3724/SP.J.1146.2013.01019

BARRON J L, FLEET D J, and CHEMIN S. Performance of optical flow techniques[C]. IEEE International Conference on Computer Vision and Pattern Recognition, Champaign, USA, 2002: 236–242. doi: 10.1109/CVPR.1992.223269.

施引文献

资源附件(0)

访问统计