Joint Symbol Detection Algorithm for Multi-antenna Signals over Flat-fading Channels Based on Variational Bayes
-
摘要: 该文针对平坦衰落信道下存在信道参数差异的多天线接收信号联合参数估计和符号检测问题,提出一种基于变分贝叶斯的联合处理算法。算法直接利用多个接收数据流进行信息符号的估计,抑制传统信号合成与解调解耦处理带来的性能损失。将问题建模为已知多组观测数据条件下发送符号、信道传输时延、信道增益和噪声功率的联合最大后验估计问题。基于变分贝叶斯理论对该最大后验进行近似求解,在相对熵最小化的准则下,推导得到了各个待估参数解析形式的近似后验分布——变分分布。所提算法无需计算各参数精确的点估计值,而是采用信道参数和信息符号变分分布迭代处理的方式进行联合求解。仿真结果表明,所提算法通过多信号、多参数的联合处理能够获得优于经典解耦处理和部分联合处理技术的系统误码率性能,且在接收天线数目较多和观测数据长度较短时性能优势体现更加明显。Abstract: For the issue of joint parameter estimation and symbol detection for multi-antenna signals with channel parameters difference over flat-fading channels, a new joint processing scheme is proposed based on the Variational Bayes (VB) method. The proposed scheme uses directly multiple received signals for the estimation of information symbols, restraining the information loss in conventional decoupled scheme of signals combination and demodulation. The problem is modeled as the joint Maximum A Posteriori (MAP) estimation of information symbols, time-delays, complex channel gains, and noise powers, given multiple observations, and approximately solved by means of VB approach. Based on the criterion of minimum relative entropy, analytical-form of the approximate distributions, i.e., variational distributions, for all unknown parameters are derived. There is no need to determine accurate point estimates of the parameters. Instead, the proposed scheme proceeds iteratively by alternating between the variational distributions of channel parameters and the information symbols. Simulation results show that the proposed joint processing scheme has significant performance improvements in comparison with conventional decoupled or partly joint processing schemes especially with large array sizes and short signal lengths.
-
Key words:
- Multi-antenna arraying /
- Flat-fading /
- Joint processing /
- Variational Bayes
-
表 1 算法流程
步骤1 初始化相关参数
令 $i = 0$, ${\bar s_n} = s_n^0$, $\left\langle {{{\left| {{s_n}} \right|}^2}} \right\rangle = {\left| {s_n^0} \right|^2}$, ${\beta _p} = 1$, $w_p^m = {1 / M}$,
${\alpha _p} = {1 / P}$, ${\rho _p} = {\delta _p} = {a_p} = {c_p} = {10^{ - 10}}$;步骤2 计算各路信道复增益的变分后验均值 ${\mu _p}$和方差 ${\lambda _p}$; 步骤3 更新时延加权因子 $w_p^m$; 步骤4 计算 ${\beta _p}$的后验均值 ${\bar \beta _p}$; 步骤5 计算 ${\alpha _p}$的后验均值 ${\bar \alpha _p}$; 步骤6 计算符号序列的后验概率 $q({s_n} = s)$,并进一步计算发送
符号的1阶/2阶统计量 ${\bar s_n}$和 $\left\langle {{{\left| {{s_n}} \right|}^2}} \right\rangle $;步骤7 令 $i = i + 1$; 步骤8 若前后两次关于 ${\bar{ {s}}}$的估计值误差小于 ${10^{ - 6}}$或 $i$大于 $20$,则
结束循环,否则重新从步骤2开始;步骤9 利用收敛后得到的信道估计结果进行符号判决。 表 2 本文算法与合成算法、现有联合处理算法运算量对比
算法 操作说明 乘法运算次数 SC EM&ImM2M4 信号合成 $\cal{O}(PN{I_{{\rm{sump}}}})$ 同步运算 $\cal{O}[PN(2M + {N_{\operatorname{intp} }}/2)]$ 权值估计 $\cal{O}(PN)$ BC EM&SS 波形校准及信号合并 $\cal{O}[PMN(M + {N_{{\rm{intp}}}}/2){I_{{\rm{sump}}}}]$ 同步运算 $\cal{O}[N(2M + {N_{{\rm{intp}}}}/2)]$ 权值估计 $\cal{O}(P{N^3})$ Shen&ImM2M4 多路联合校准 $\cal{O}(PMN{I_{{\rm{em}}}})$ 权值估计 $\cal{O}(PN{I_{{\rm{em}}}})$ 本文算法 信道参数估计 $\cal{O}(PMN{I_{{\rm{vb}}}})$ 符号估计 $\cal{O}(PMN\left| \cal{S} \right|{I_{{\rm{vb}}}})$ -
ZHANG Kai, YU Hongyi, HU Yunpeng, et al. ML-based iterative approach for blind frequency domain equalization and combination over sparse channels[J]. IEEE Communications Letters, 2018, 22(1): 193–196 doi: 10.1109/LCOMM.2017.2672963 张凯, 于宏毅, 胡赟鹏, 等. 基于EM-SBL迭代的稀疏SIMO信道频域盲均衡算法[J]. 电子学报, 2018, 46(2): 372–380 doi: 10.3969/j.issn.0372-2112.2018.02.016ZHANG Kai, YU Hongyi, HU Yunpeng, et al. Blind frequency-domain equalization for sparse SIMO channels based on iterative EM-SBL algorithm[J]. Acta Electronica Sinica, 2018, 46(2): 372–380 doi: 10.3969/j.issn.0372-2112.2018.02.016 YAO Kai, REED C, HUDSON R E, et al. Blind beamforming on a randomly distributed sensor array system[J]. IEEE Journal on Selected Areas in Communications, 1998, 16(8): 1555–1567 doi: 10.1109/49.730461 GE Xiaohu, TU Song, MAO Guoqiang, et al. 5G ultra-dense cellular networks[J]. IEEE Wireless Communications, 2016, 23(1): 72–79 doi: 10.1109/MWC.2016.7422408 WANG Peng, MAO Guoqiang, LIN Zihuai, et al. Performance analysis of raptor codes under maximum likelihood decoding[J]. IEEE Transactions on Communications, 2016, 64(3): 906–917 doi: 10.1109/TCOMM.2016.2522403 ZI Ran, GE Xiaohu, THOMPSON J, et al. Energy efficiency optimization of 5G radio frequency chain systems[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 758–771 doi: 10.1109/JSAC.2016.2544579 GE Xiaohu, ZI Ran, XIONG Xusheng, et al. Millimeter wave communications with OAM-SM scheme for future mobile networks[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 2163–2177 doi: 10.1109/JSAC.2017.2720238 NATARAJAN S, BARBOSA D, BARRACA J P, et al. SKA Telescope Manager (TM): Status and architecture overview[C]. 2016 SPIE Astronomical Telescopes+Instrumentation. International Society for Optics and Photonics, Edinburgh, UK, 2016: 991302-991302-10. 张凯, 于宏毅, 沈彩耀, 等. 随机布局多天线信号联合时差估计Cramer-Rao下界[J]. 信号处理, 2013, 29(4): 497–502ZHANG Kai, YU Hongyi, SHEN Caiyao, et al. Cramer-Rao lower bound for joint time delay estimation in a randomly distributed antenna array[J]. Journal of Signal Processing, 2013, 29(4): 497–502 LEE C H, CHEUNG K M, and VILNROTTER V A. Fast eigen-based signal combining algorithms for large antenna arrays[C]. 2003 IEEE Aerospace Conference. Big Sky, USA, 2003: 1123–1129. STEIN S. Algorithm for ambiguity function processing[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(3): 588–599 doi: 10.1109/TASSP.1981.1163621 漆雪梅, 沈彩耀, 张效义. SIMO 信道中基于奇异值分解的盲信噪比估计算法[J]. 信号处理, 2011, 27(4): 588–599QI Xuemei, SHEN Caiyao, and ZHANG Xiaoyi. A blind SNR estimation algorithm based on SVD over SIMO channels[J]. Journal of Signal Processing, 2011, 27(4): 588–599 SHEN Caiyao and YU Hongyi. Time-delay alignment technique for a randomly distributed sensor array[J]. IET Communications, 2011, 5(8): 1068–1072 doi: 10.1049/iet-com.2010.0671 CHUGG K M and POLYDOROS A. MLSE for an unknown channel. I. optimality considerations[J]. IEEE Transactions on Communications, 1996, 44(7): 836–846 doi: 10.1109/26.508303 CLARK M V, GREENSTEIN L J, KENNEDY W K, et al. Optimum linear diversity receivers for mobile communications[J]. IEEE Transactions on Vehicular Technology, 1994, 43(1): 47–56 doi: 10.1109/25.282265 WIPF D. Don’t relax: Why non-convex algorithms are often needed for sparse estimation?[R]. ICCV2013, Sydney Australia. BISHOP C M. Pattern Recognition and Machine Learning[M]. New York: Springer, 2006: 461–517. THEMELIS K E, RONTOGIANNIS A A, and KOUTROUMBAS K D. A variational Bayes framework for sparse adaptive estimation[J]. IEEE Transactions on Signal Processing, 2014, 62(18): 4723–4736 doi: 10.1109/TSP.2014.2338839 NOELS N, LOTTICI V, DEJONGHE A, et al. A theoretical framework for soft-information-based synchronization in iterative (turbo) receivers[J]. EURASIP Journal on Wireless Communications and Networking, 2005, 2005(2): 117–129 doi: 10.1155/WCN.2005.117 IJAZ A, AWOSEYILA A B, and EVANS B G. Improved SNR estimation for BPSK and QPSK signals[J]. Electronics Letters, 2009, 45(16): 858–859 doi: 10.1049/el.2009.1759 SHEN Zhixiang, YU Hongyi, HU Yunpeng, et al. Joint symbol detection for multi-receiver without signal synchronization and array alignment[J]. IEEE Communications Letters, 2014, 18(10): 1755–1758 doi: 10.1109/LCOMM.2014.2352644 ANDERSIN M, MANDAYAM N B, and YATES R D. Subspace based estimation of the signal to interference ratio for TDMA cellular systems[C]. 1996 IEEE Vehicular Technology Conference. Atlanta, USA, 1996: 1155–1159. TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211–244 doi: 10.1162/15324430152748236 -





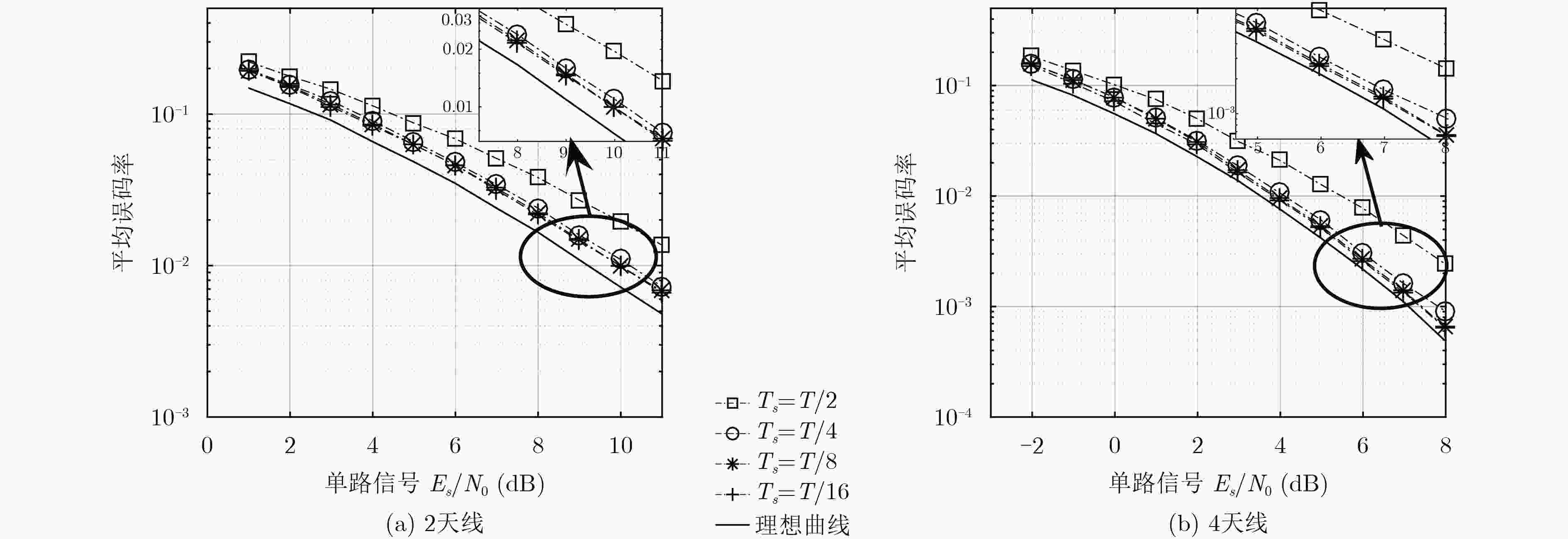
 下载:
下载:
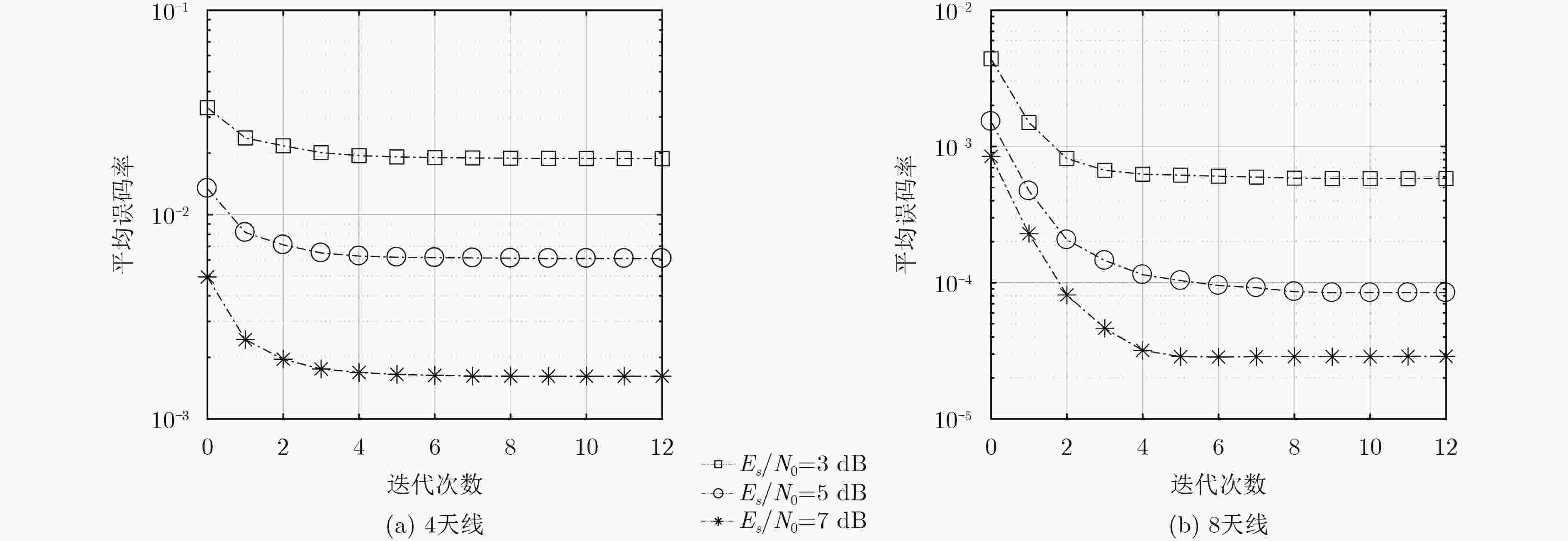
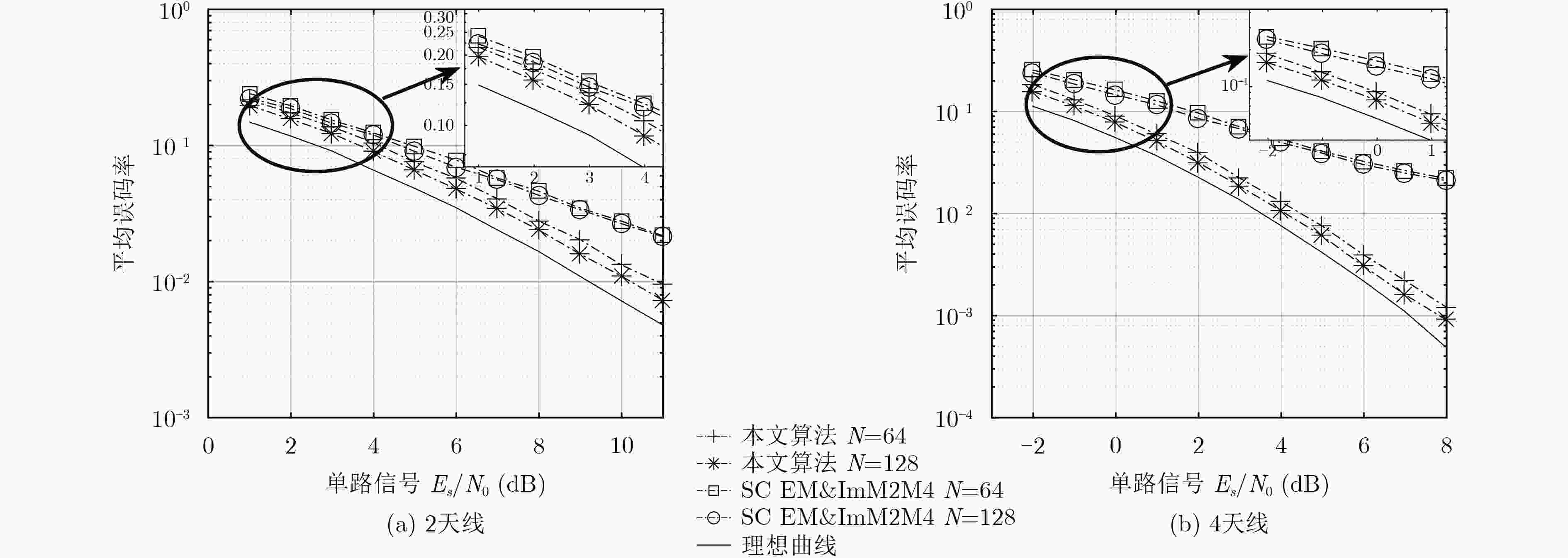
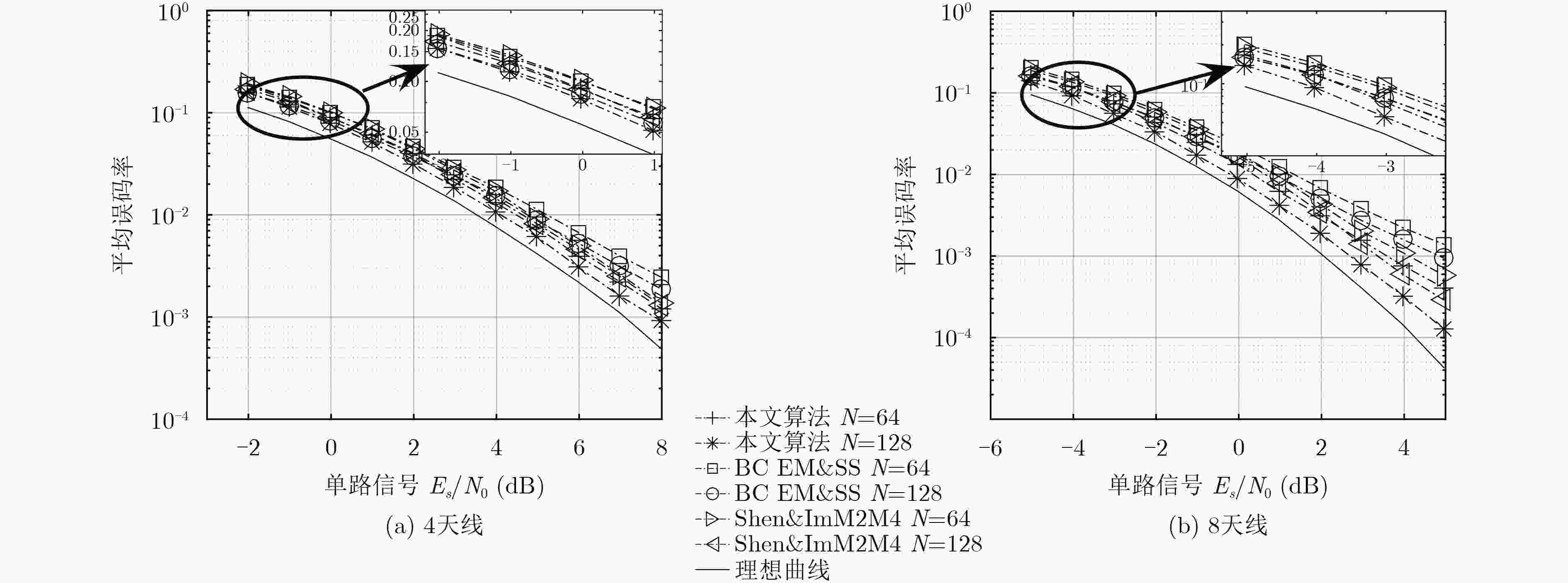


 下载:
下载:
