Hyperspectral Image Compression Based on Adaptive Band Clustering Principal Component Analysis and Back Propagation Neural Network
-
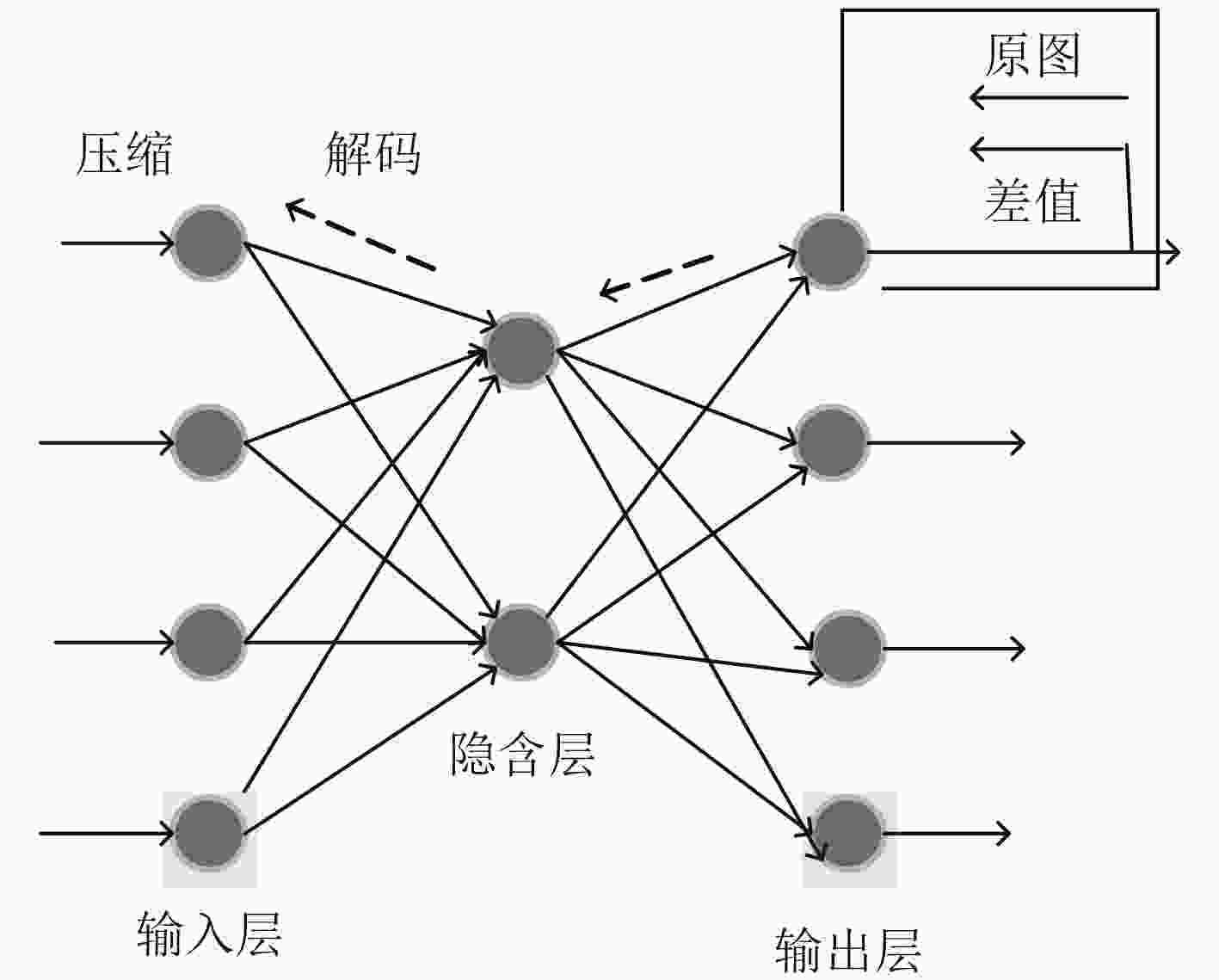
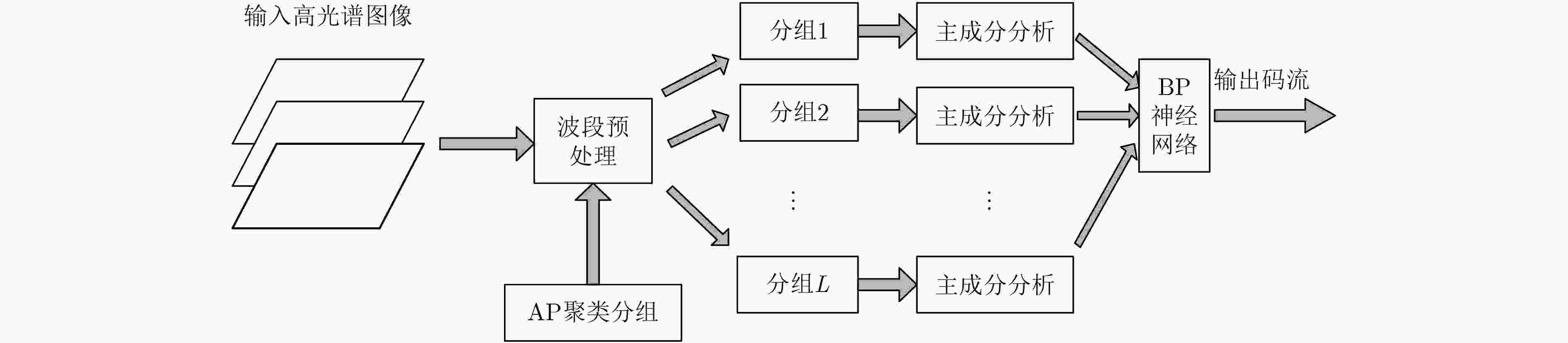
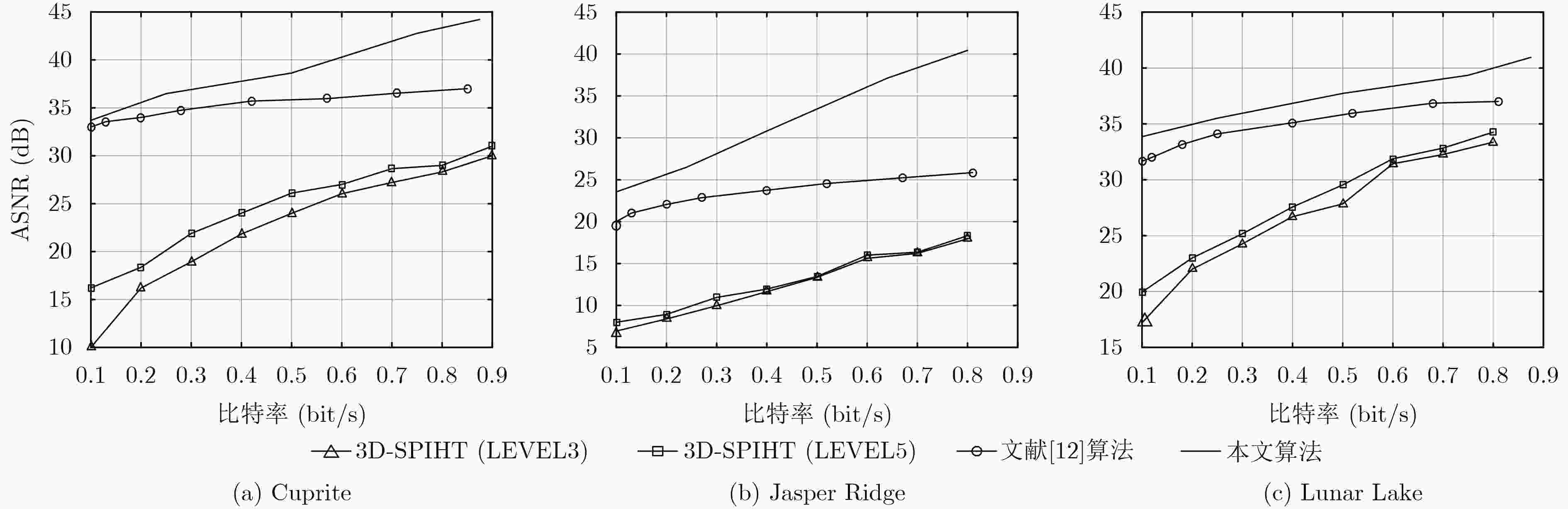
摘要: 高光谱遥感图像具有丰富的光谱信息,数据量大。为了能够有效地利用高光谱图像数据,促进高光谱遥感技术的发展,该文提出一种基于自适应波段聚类主成分分析(PCA)与反向传播(BP)神经网络相结合的高光谱图像压缩算法。算法利用近邻传播(AP)聚类算法对波段进行自适应聚类,对聚类后的各个分组分别进行PCA运算,最后利用BP神经网络对所有主成分进行编码压缩。该文的创新点在于BP神经网络压缩图像时,在训练步骤过程中,误差反向传播是用原图与输出作差值,再反向调整各层的权值、阈值。对高光谱图像进行波段聚类,不仅能够有效地利用谱间相关性,提高压缩性能,还可以降低PCA的运算量。实验结果表明,该文算法与其它现有算法比较,在相同压缩比下,其光谱角更小,信噪比更高。Abstract: Hyperspectral remote sensing images have a wealth of spectral information and a huge universe of data. In order to utilize effectively hyperspectral image data and promote the development of hyperspectral remote sensing technology, a hyperspectral image compression algorithm based on adaptive band clustering Principal Component Analysis (PCA) and Back Propagation (BP) neural network is proposed. Affinity Propagation (AP) clustering algorithm for adaptive band clustering is used, and PCA is performed on the each band group respectively after clustering. Finally, all principal components are encoded and compressed by BP neural network. The innovation point lies in BP neural network compressed image during the training step, the error of backpropagation is to compare difference between the original image and the output image, and then adjust the weight and threshold of each layer in the reverse direction. Band clustering of hyperspectral images can not only effectively utilize the spectral correlation and improve the compression performance, but also reduce the computational complexity of PCA. Experimental results investigate that the proposed algorithm achieve a better performance on Signal-to-Noise Ratio (SNR) and spectral angle than other algorithm under the same compression ratio.
-
表 1 Cuprite波段聚类分组结果
分组号 1 2 3 4 5 6 各组波段划分 1~17 18~32 33~60 61~74 75~96 97~117 组内相关性 0.9738 0.9998 0.9998 0.9948 0.9997 0.9902 分组号 7 8 9 10 11 12 各组波段划分 118~145 146~161 162~177 178~191 192~202 203~224 组内相关性 0.9961 0.9963 0.9963 0.9925 0.9828 0.8134 不分组时波段间相关性 0.7759 表 2 Jasper Ridge波段聚类分组结果
分组号 1 2 3 4 各组波段划分 1~24 25~36 37~105 106~113 组内相关性 0.9679 0.9662 0.9663 0.9662 分组号 5 6 7 8 各组波段划分 114~121 122~153 154~166 167~224 组内相关性 0.9665 0.9663 0.9663 0.9664 不分组时波段间相关性 0.6939 表 3 Lunar Lake波段聚类分组结果
分组号 1 2 3 4 5 各组波段划分 1~19 20~39 40~70 71~107 108~111 组内相关性 0.9704 0.9993 0.9993 0.9972 0.5797 分组号 6 7 8 9 10 各组波段划分 112~155 156~166 167~206 207~221 222~224 组内相关性 0.9742 0.4823 0.9934 0.9868 0.8380 不分组时波段间相关性 0.6413 表 4 光谱角对比
比特率(bit/s) Cuprite Jasper Ridge Lunar Lake 本文算法 文献[12]算法 3D-SPIHT 本文算法 文献[12]算法 3D-SPIHT 本文算法 文献[12]算法 3D-SPIHT 0.1 0.4842 0.5922 18.4829 1.5030 4.0054 43.8099 0.5151 0.6494 4.7773 0.2 0.3898 0.5179 6.2616 1.4196 3.1861 24.8005 0.4620 0.5847 1.1188 0.4 0.2820 0.4531 1.8106 1.3757 2.8051 8.2692 0.3331 0.5217 0.8408 0.7 0.2697 0.3956 0.7953 1.2893 2.4240 3.3733 0.3325 0.4599 0.4622 -
BIOUCA-DIAS J, PLAZA A, CAMPS-VALLS G, et al. Hyperspectral remote sensing data analysis and future challenges[J].IEEE Geoscience and Remote Sensing Magazine, 2013, 1(2): 6–36 doi: 10.1109/MGRS.2013.2244672 SHEN Hongda, PAN W D, WU Dongsheng, et al. Fast Golomb coding parameter estimation using partial data and its application in hyperspectral image compression[C]. Southeastcon, Norfolk, USA, 2016: 1–7. FU Wei, LI Shutao, FANG Leyuan, et al. Adaptive spectral–spatial compression of hyperspectral image with sparse representation[J]. IEEE Transactions on Geoscience&Remote Sensing, 2017, 55(2): 671–682 doi: 10.1109/TGRS.2016.2613848 LANDGREBE D. Hyperspectral image data analysis[J]. IEEE Signal Processing Magazine, 2002, 19(1): 17–28 doi: 10.1109/79.974718 陈善学, 韩勇, 于佳佳, 等. 矢量维数分割量化的高光谱图像压缩方法[J]. 系统工程与电子技术, 2013, 35(9): 1989–1993 doi: 10.3969/j.issn.1001-506x.2013.09.31CHEN Shanxue, HAN Yong, YU Jiajia, et al. Compression algorithm of hyperspectral image based on vector dimension segmentation quantization[J]. Journal of Systems Engineering and Electronics, 2013, 35(9): 1989–1993 doi: 10.3969/j.issn.1001-506x.2013.09.31 KARAMI A, YAZDI M, and MERCIER G. Compression of hyperspectral images using discrete wavelet transform and tucker decomposition[J]. IEEE Journal on Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(2): 444–450 doi: 10.1109/JSTARS.2012.2189200 MIELIKAINEN J and HUANG B. Lossless compression of hyperspectral images using clustered linear prediction with adaptive prediction length[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(6): 1118–1121 doi: 10.1109/LGRS.2012.2191531 ZHU Shiping and ZONG Xianzi. Fractal lossy hyperspectral image coding algorithm based on prediction[J]. IEEE Access, 2017, 5: 21250–21257 doi: 10.1109/ACESS.2017.2755681 SHEN Hongda, PAN W D, and WU Dongsheng. Predictive lossless compression of regions of interest in hyperspectral images with no-data regions[J]. IEEE Transactions on Geoscience&Remote Sensing, 2016, 55(1): 173–182 doi: 10.1109/TGRS.2016.2603527 WEN Jia, MA Caiwen, and ZHAO Junsuo. FIVQ algorithm for interference hyper-spectral image compression[J].Optics Communications, 2014, 322(8): 97–104 doi: 10.1016/j.optcom.2014.02.016 韩力群. 人工神经网络理论、设计及应用[M]. 第2版, 北京: 化学工业出版社, 2007: 第3章.HAN Liqun. Artificial Neural Network Theory, Design and Application[M]. Second Edition, Beijing: Chemical Press, 2007: Chapter three. 吴倩, 张荣, 徐大卫. 基于稀疏表示的高光谱数据压缩算法[J]. 电子与信息学报, 2015, 37(1): 78–84 doi: 10.11999/JEIT140214WU Qian, ZHANG Rong, and XU Dawei. Hyperspectral data compression based on sparse representation[J]. Journal of Electronica&Information Technology, 2015, 37(1): 78–84 doi: 10.11999/JEIT140214 高放, 孙长建, 邵庆龙, 等. 基于K-均值聚类和传统递归最小二乘法的高光谱图像无损压缩[J]. 电子与信息学报, 2016, 38(11): 2709–2714 doi: 10.11999/JEIT151439GAO Fang, SUN Changjian, SHAO Qinglong, et al. Lossless compression of hyperspectral image using K-means clustering and conventional recursive least-squares predictor[J]. Journal of Electronica&Information Technology, 2016, 38(11): 2709–2714 doi: 10.11999/JEIT151439 FOWLER J E. Compressive-projection principal component analysis[J]. IEEE Transactions on Image Processing, 2009, 18(10): 2230–2242 doi: 10.1109/TIP.2009.2025089 WEI Jia. Application of hybrid back propagation neural network in image compression[C]. International Conference on Intelligent Computation Technology and Automation, Nanchang, China, 2016: 209–212. 闫红梅, 吴冬梅. 改进BP网络在超光谱图像压缩中的应用[J]. 图学学报, 2013, 34(5): 110–114 doi: 10.3969/j.issn.2095-302X.2013.05.022YAN Hongmei and WU Dongmei. Application of improved BP neural network in hyperspectral image compression[J]. Journal of Engineering Graphics, 2013, 34(5): 110–114 doi: 10.3969/j.issn.2095-302X.2013.05.022 -





 下载:
下载:


 下载:
下载:
