Fast Multi-objective Antenna Design Based on Improved Back Propagation Neural Network Surrogate Model
-
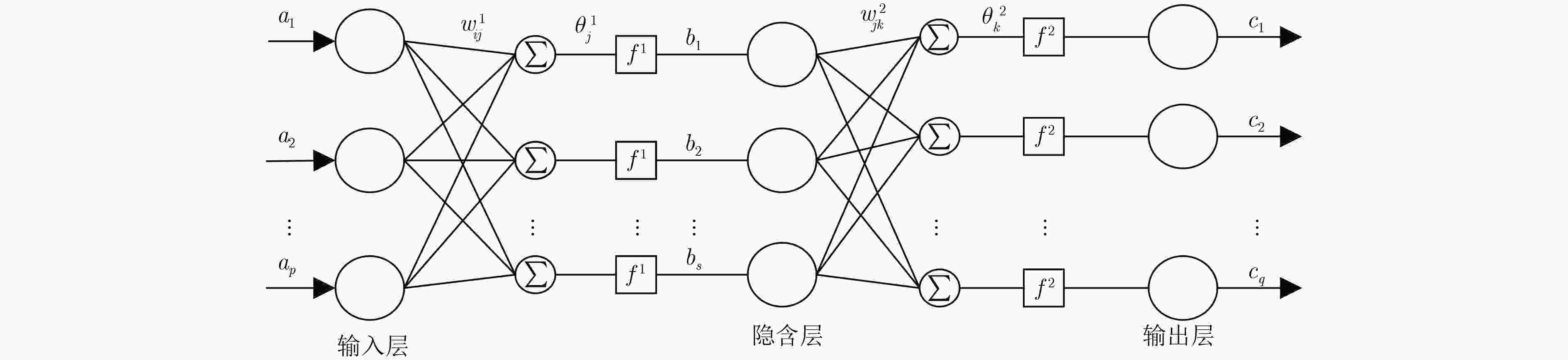
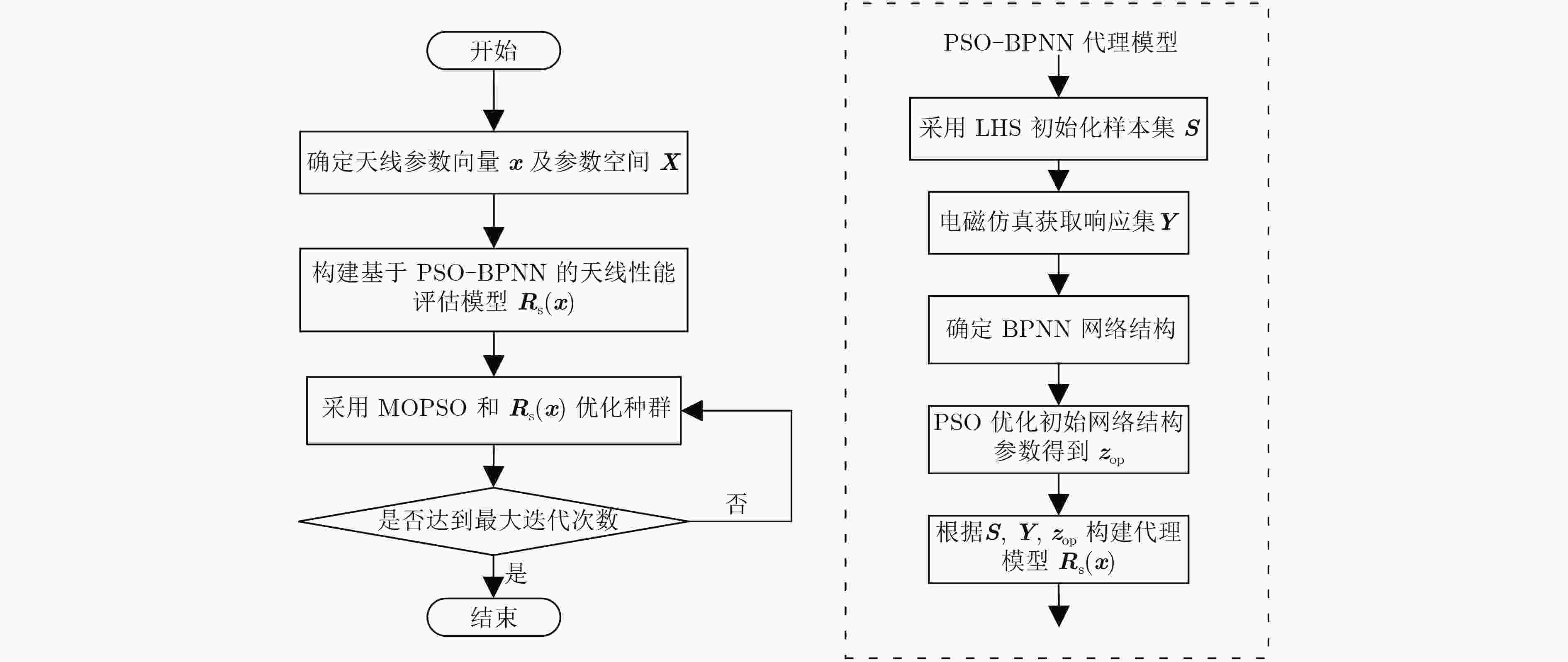
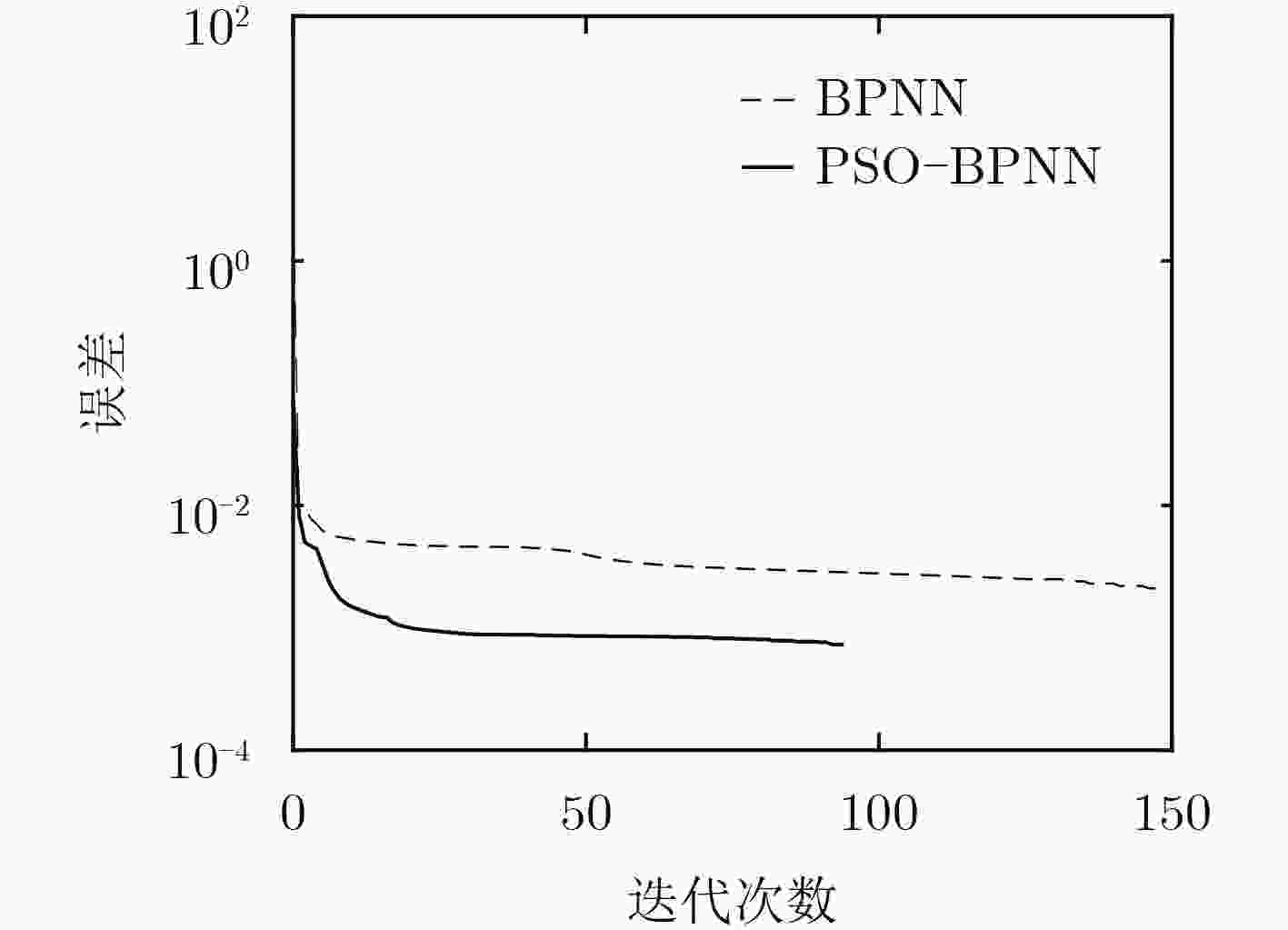
摘要: 针对传统天线设计方法计算代价较大的缺陷，该文构建基于反向传播神经网络(BPNN)的新型天线代理模型。为解决BPNN训练易陷入局部最优的问题，采用粒子群优化(PSO)算法来改善神经网络初始结构参数，进而构建PSO-BPNN天线代理模型，并基于该模型提出多参数天线结构的快速多目标设计方法。设计实例表明，该方法在预测精度以及计算代价等方面优于现有的常用天线设计方法。所提方法对处理复杂高维参数空间天线设计问题具有实用价值。Abstract: Focusing on the problem of reducing the large computation cost of traditional antenna design methods, a new surrogate model based on Back Propagation Neural Networks (BPNN) is constructed. In order to solve the problem of easily falling into local optimum in BPNN, a PSO-BPNN surrogate model is developed by improving initial structural parameters of neural networks and applied to fast multi-objective optimization design of multi-parameter antenna structures. The design results show that the proposed PSO-BPNN outperforms other existing antenna surrogate models in terms of prediction accuracy and prediction speed. The proposed method is of value in dealing with complex antenna designs with high-dimensional parameter space.
-
表 1 设计参数初始范围
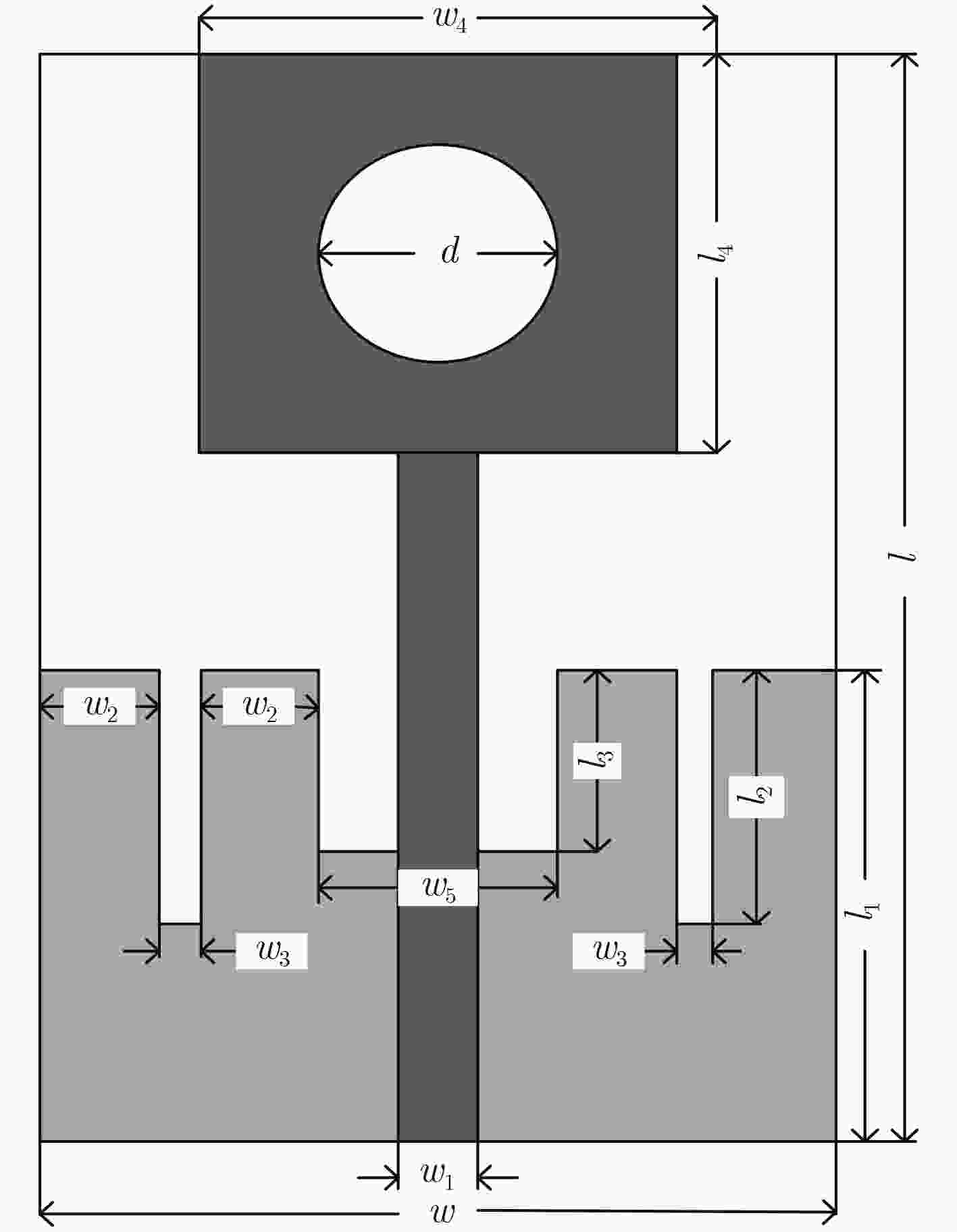
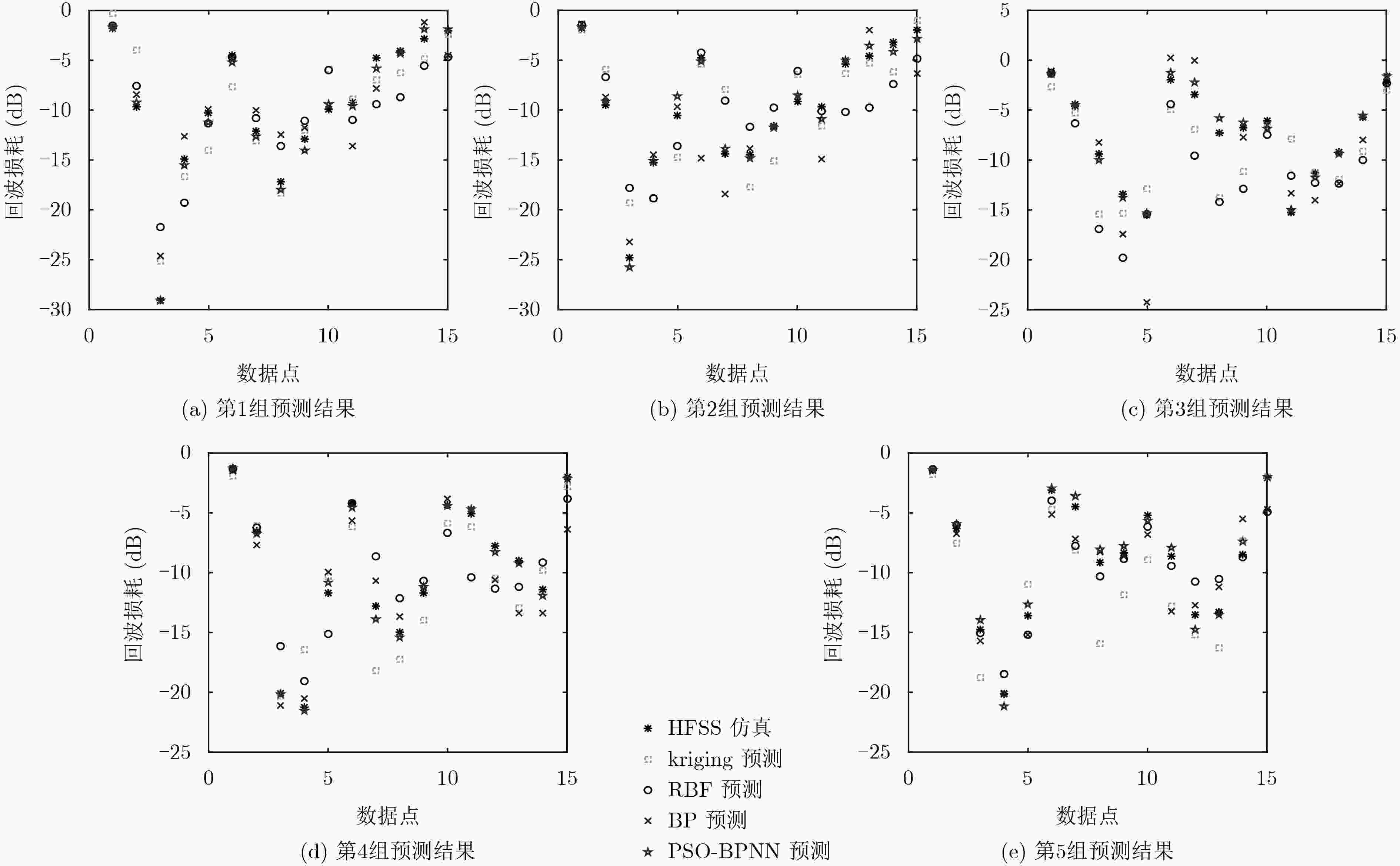
参数 d l l1 l2 l3 范围(mm) [7,10] [26,34] [11,14] [8,10] [6,8] 参数 l4 w w1 w2 w3 范围(mm) [10,14] [17,23] [2,4] [2,4] [0.5,1.5] 
下载: 导出CSV
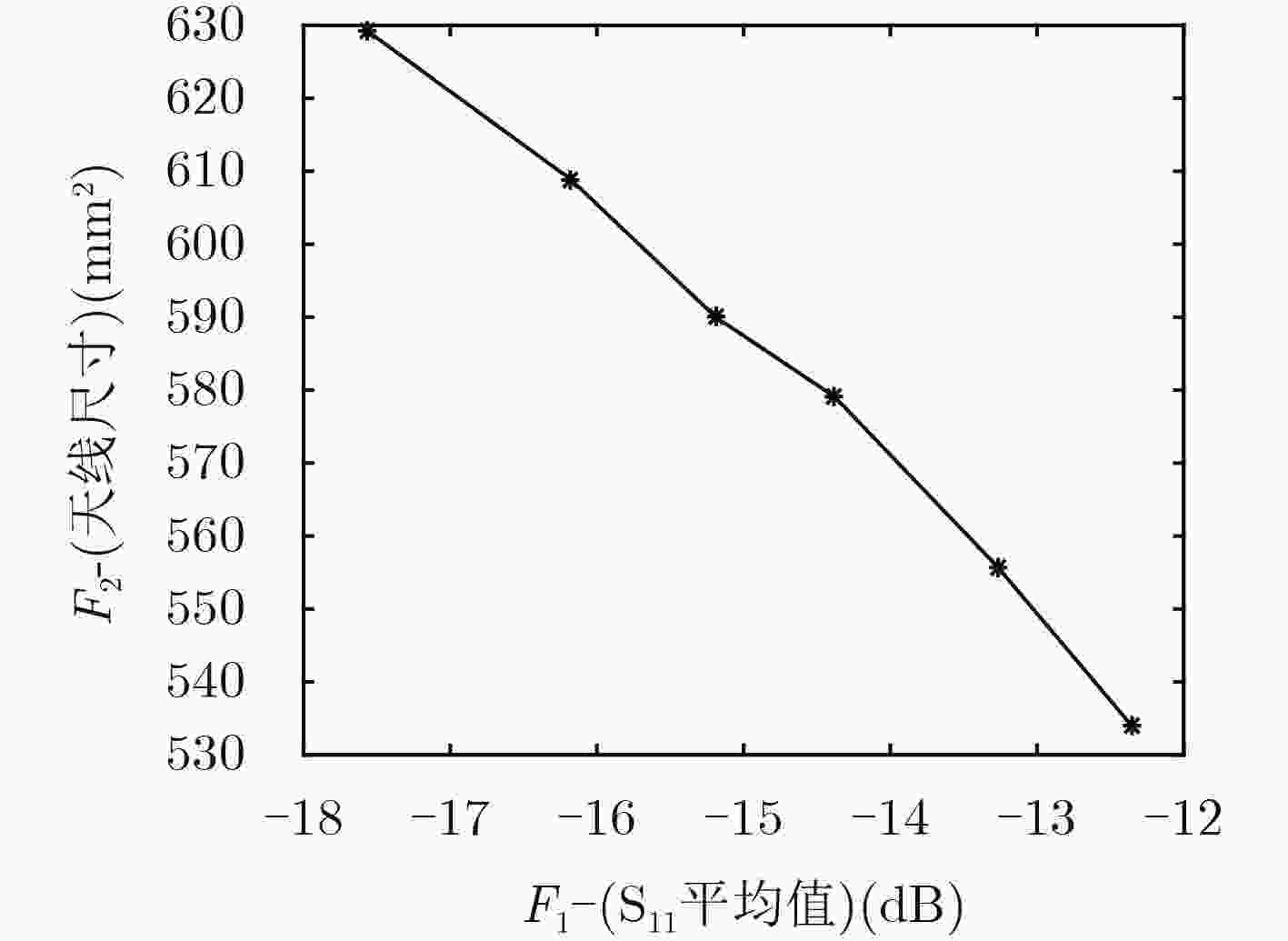
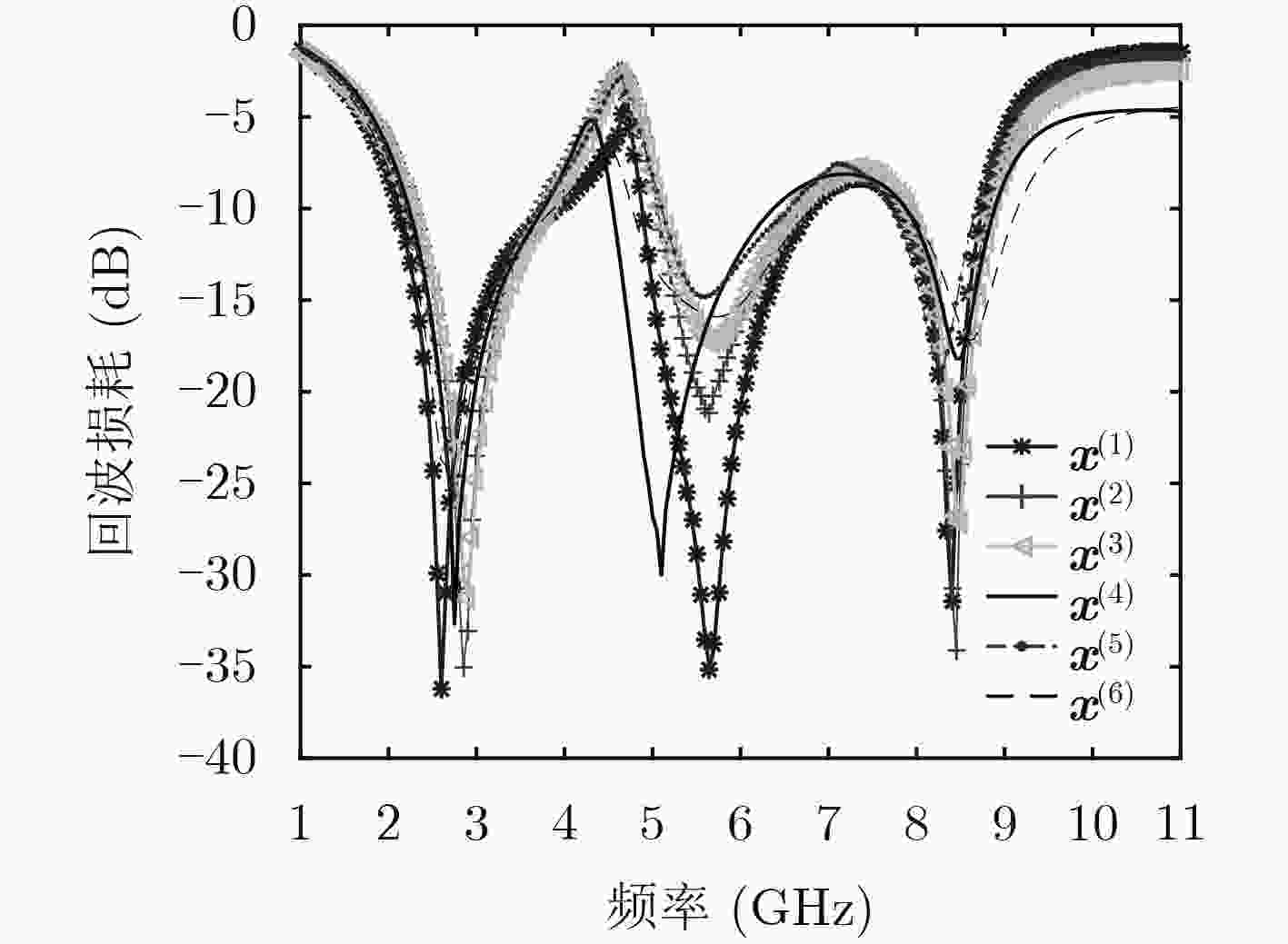
表 4 平面3频带天线的的Pareto最优设计
设计 ${{{x}}^{(1)}}$ ${{{x}}^{(2)}}$ ${{{x}}^{(3)}}$ ${{{x}}^{(4)}}$ ${{{x}}^{(5)}}$ ${{{x}}^{(6)}}$ F1(dB) –17.57 –16.18 –15.19 –14.19 –13.27 –12.35 F2(mm2) 629.28 608.94 590.00 580.14 555.84 533.90 d 8.7 8.8 8.4 8.6 8.3 9.4 l 30.4 30.6 29.5 29.3 28.8 28.1 l1 11.8 12.9 12.8 12.4 10.9 11.2 l2 9.0 8.8 9.0 9.2 8.8 9.7 l3 6.4 6.8 6.8 6.8 7.0 6.6 l4 11.5 11.5 11.1 12.3 10.9 11.0 w 20.7 19.9 20.0 19.8 19.3 19.0 w1 3.1 3.3 3.2 3.4 3.0 2.9 w2 3.0 3.1 3.8 3.4 3.2 3.4 w3 1.0 1.0 0.9 0.8 1.1 1.2
下载: 导出CSV
表 5 代理模型与HFSS所获得的Pareto最优解集的目标值F1比较
代理模型 ${{{x}}^{(1)}}$ ${{{x}}^{(2)}}$ ${{{x}}^{(3)}}$ ${{{x}}^{(4)}}$ ${{{x}}^{(5)}}$ ${{{x}}^{(6)}}$ HFSS –17.46 –15.75 –15.01 –14.69 –13.50 –12.53 BPNN –19.19 –17.90 –16.97 –16.04 –15.13 –14.36 PSO-BPNN –17.57 –16.18 –15.19 –14.19 –13.27 –12.35 误差率1(%) 9.91 13.65 13.06 9.19 12.07 14.60 误差率2(%) 0.63 2.73 1.20 3.40 1.70 1.44
下载: 导出CSV
-
MOHAMMED H J, ABDULLAH, A S, ALI R S, et al. Design of a uniplanar printed triple band-rejected ultra-wideband antenna using particle swarm optimisation and the firefly algorithm[J]. IET Microwaves,Antennas&Propagation, 2016, 10(1): 31–37 doi: 10.1049/iet-map.2014.0736 CHOI K, JANG D, KANG S, et al. Hybrid algorithm combing genetic algorithm with evolution strategy for antenna design[J]. IEEE Transactions on Magnetics, 2016, 52(3): 7209004 doi: 10.1109/TMAG.2015.2486043 GOUDOS S K, KALIALAKIS C, and MITTRA R. Evolutionary algorithms applied to antennas and propagation: A review of state of the art[J]. International Journal of Antennas and Propagation, 2016, 2016(4): 1–12 doi: 10.1155/2016/1010459 KOZIEL S and OGURTSOY S. Multi-objective design of antennas using variable-fidelity simulations and surrogate models[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(12): 5931–5939 doi: 10.1109/TAP.2013.2283599 陈晓辉, 裴进明, 郭欣欣, 等. 一种基于多维均匀采样与Kriging模型的天线快速优化方法[J]. 电子与信息学报, 2014, 36(12): 3021–3026 doi: 10.3724/SP.J.1146.2013.01826CHEN Xiaohui, PEI Jinming, GUO Xinxin, et al. An efficient antenna optimization method based on kriging model and multidimensional uniform sampling[J]. Journal of Electronics&Information Technology, 2014, 36(12): 3021–3026 doi: 10.3724/SP.J.1146.2013.01826 DONG Jian, LI Qianqian, and DENG Lianwen. Fast multi-objective optimization of multi-parameter antenna structures based on improved MOEA/D with surrogate-assisted model[J]. AEUE-International Journal of Electronics and Communications, 2017, 72: 192–199 doi: 10.1016/j.aeue.2016.12.007 LIU Bo, ALIAKBARIAN H, MA Zhongkun, et al. An efficient method for antenna design optimization based on evolutionary computation and machine learning techniques[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(1): 7–18 doi: 10.1109/TAP.2013.2283605 JACOBS J P. Efficient resonant frequency modeling for dual-band microstrip antennas by Gaussian process regression[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 337–341 doi: 10.1109/LAWP.2014.2362937 CHEN Linglu, LIAO Cheng, LIN Wenbin, et al. Hybrid-surrogate-model-based efficient global optimization for high-dimensional antenna design[J]. Progress in Electromagnetics Research, 2012, 124(8): 85–100 doi: 10.2528/PIER11121203 MASSA A, OLIVERI G, SALUCCI M, et al. Learning-by-examples techniques as applied to electromagnetics[J]. Journal of Electromagnetic Waves and Applications, 2017, 32(4): 516–541 doi: 10.1080/09205071.2017.1402713 焦李成, 杨淑媛, 刘芳, 等. 神经网络七十年: 回顾与展望[J]. 计算机学报, 2016, 39(8): 1697–1716 doi: 10.11897/SP.J.1016.2016.01697JIAO Licheng, YANG Shuyuan, LIU Fang, et al. Seventy years beyond neural networks: retrospect and prospect[J]. Chinese Journal of Computers, 2016, 39(8): 1697–1716 doi: 10.11897/SP.J.1016.2016.01697 公茂果, 焦李成, 杨咚咚, 等. 进化多目标优化算法研究[J]. 软件学报, 2009, 20(2): 271–289 doi: 10.3724/SP.J.1001.2009.03483GONG Maoguo, JIAO Licheng, YANG Dongdong, et al. Research on evolutionary multi-objective optimization algorithms[J]. Journal of Software, 2009, 20(2): 271–289 doi: 10.3724/SP.J.1001.2009.03483 RUMELHART D E, HINTON G E, and WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(9): 533–536 doi: 10.1038/323533a0 KOLMOGOROV A N. On the representation of continuous functions of several variables by superposition of continuous functions of one variable and addition[J]. Doklady Akademii Nauk SSSR, 1957, 114(5): 953–956 doi: 10.1007/978-94-011-3030-1_56 STEIN M. Large sample properties of simulations using Latin hypercube sampling[J]. Technometrics, 1987, 29(2): 143–151 doi: 10.1080/00401706.1987.10488205 KENNEDY J and EBERHART R C. Particle swarm optimization[C]. Proceedings of IEEE International Conference on Neural Networks, Perth, Australia, 1995, 4: 1942–1948. doi: 10.1109/icnn.1995.488968. COELLO C A C, PULIDO G T, and LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256–279 doi: 10.1109/TEVC.2004.826067 DONG Jian, YU Xiaping, and HU Guoqiang. Design of a compact quad-band slot antenna for integrated mobile devices[J]. International Journal of Antennas and Propagation, 2016, 2016: 1–9 doi: 10.1155/2016/3717681 ANURDHA, PATNAIK A, and SINHA S N. Design of custom-made fractal multi-band antennas using ANN-PSO[J]. IEEE Antennas&Propagation Magazine, 2011, 53(4): 94–101 doi: 10.1109/MAP.2011.6097296 ROBINSON J and RAHMAT-SAMMI Y. Particle swarm optimization in electromagnetics[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(2): 397–407 doi: 10.1109/TAP.2004.823969 JIN Nanbo and RAHMAT-SAMMI Y. Advances in particle swarm optimization for antenna designs: Real-number, binary, single-objective and multiobjective implementations[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(3): 556–567 doi: 10.1109/TAP.2007.891552 -
图(8) / 表(6)
计量
- 文章访问数: 2021
- HTML全文浏览量: 908
- PDF下载量: 94
- 被引次数: 0
下载:
