Non-orthogonal-code Index Modulation
-
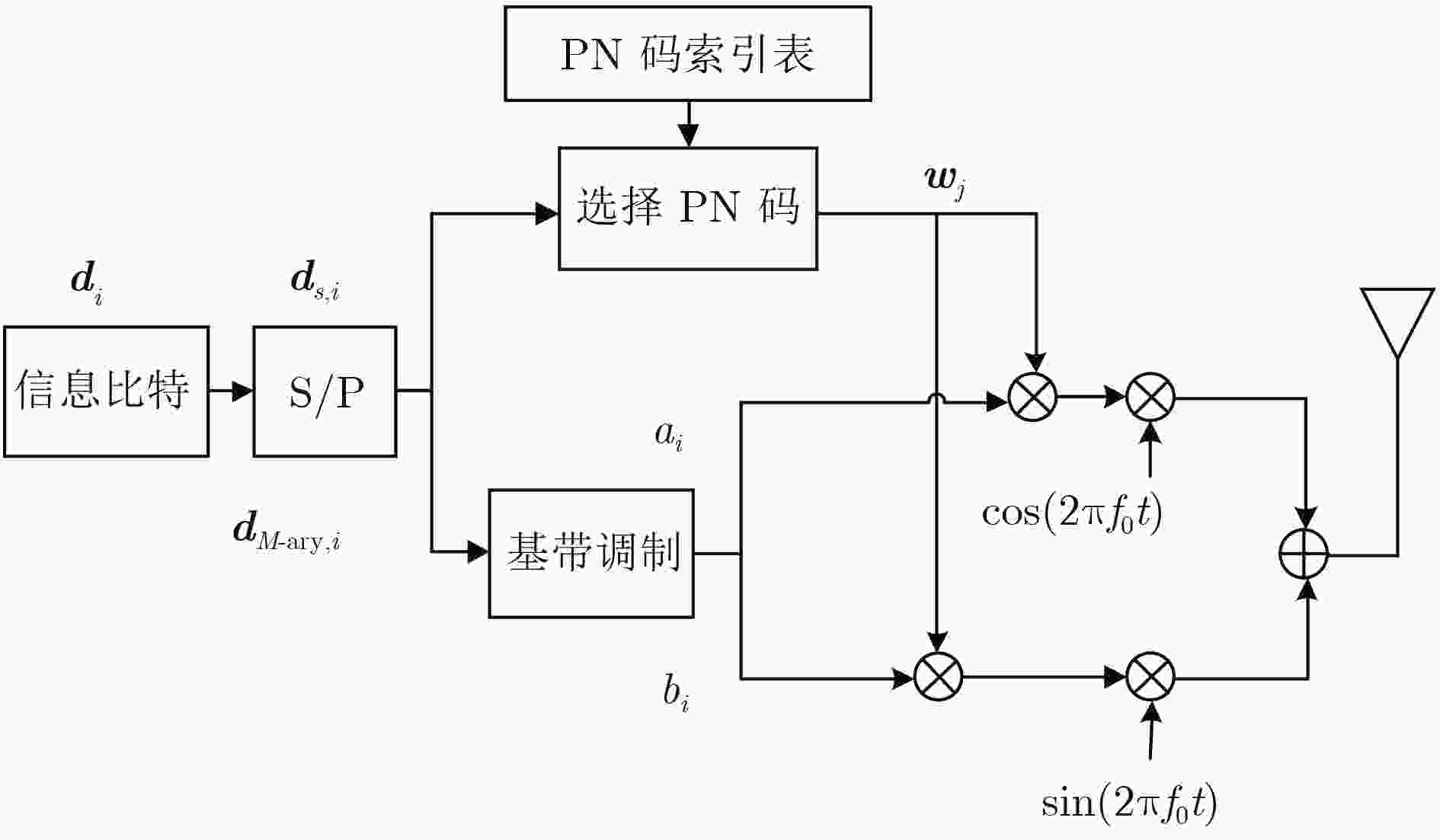
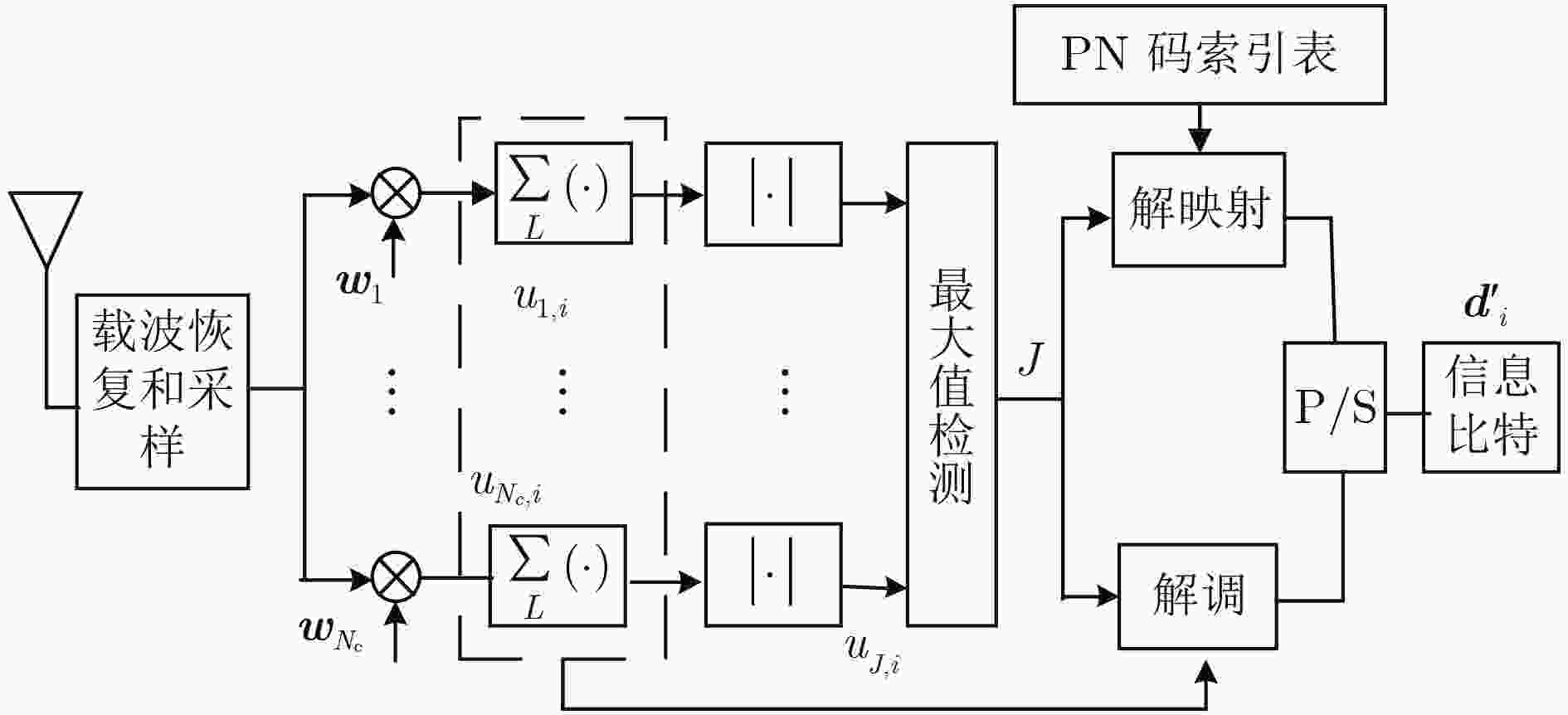
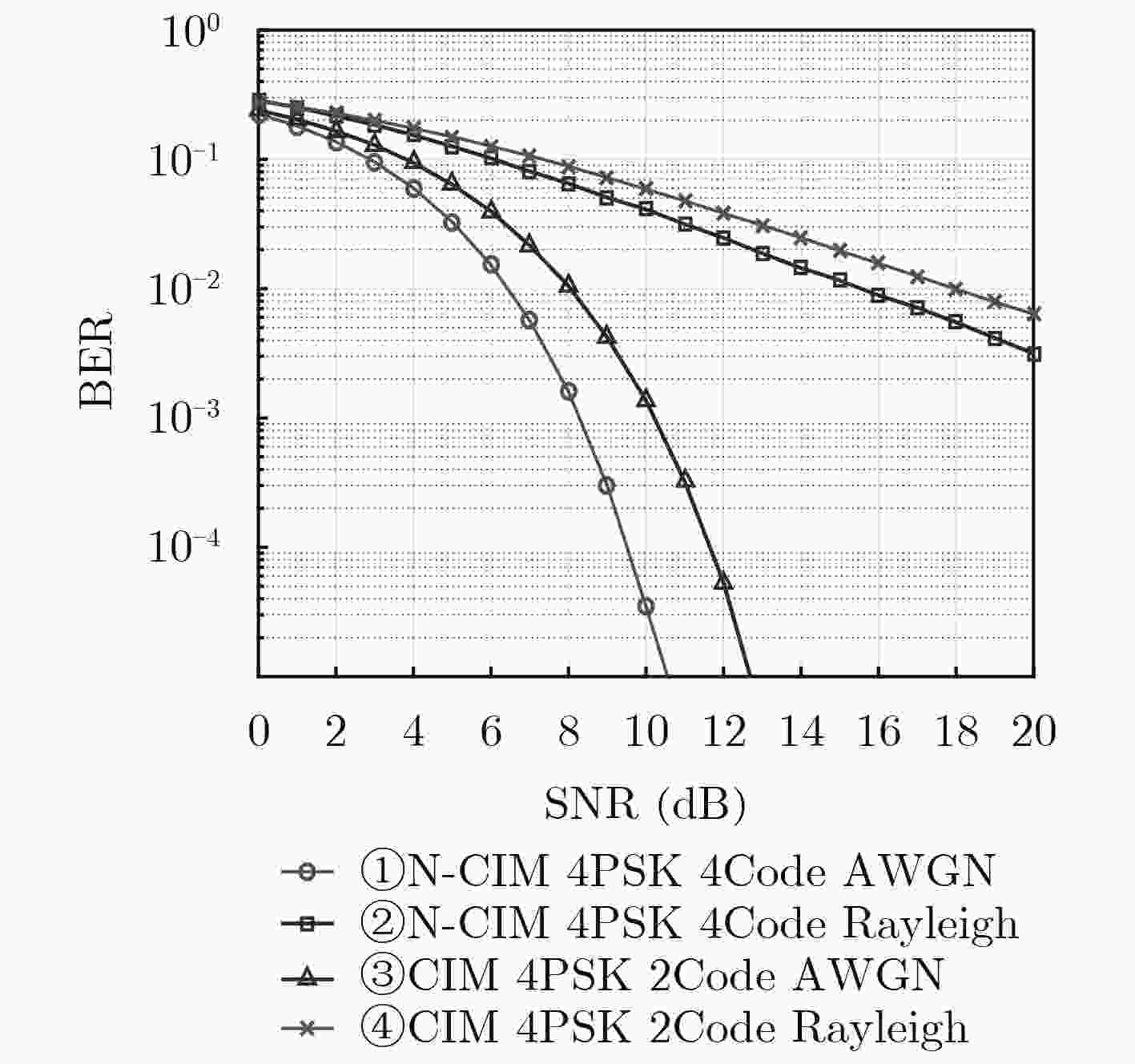
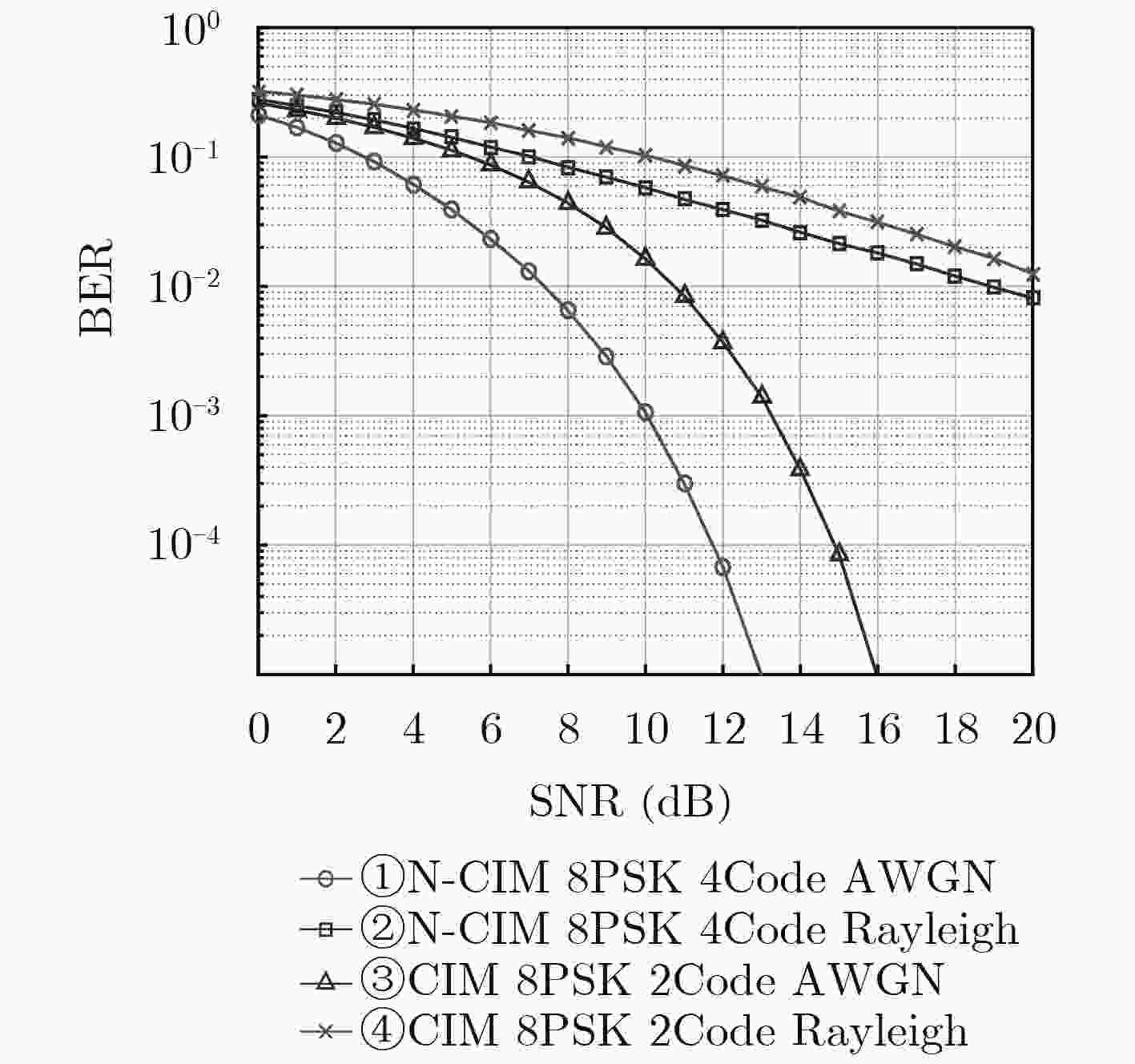
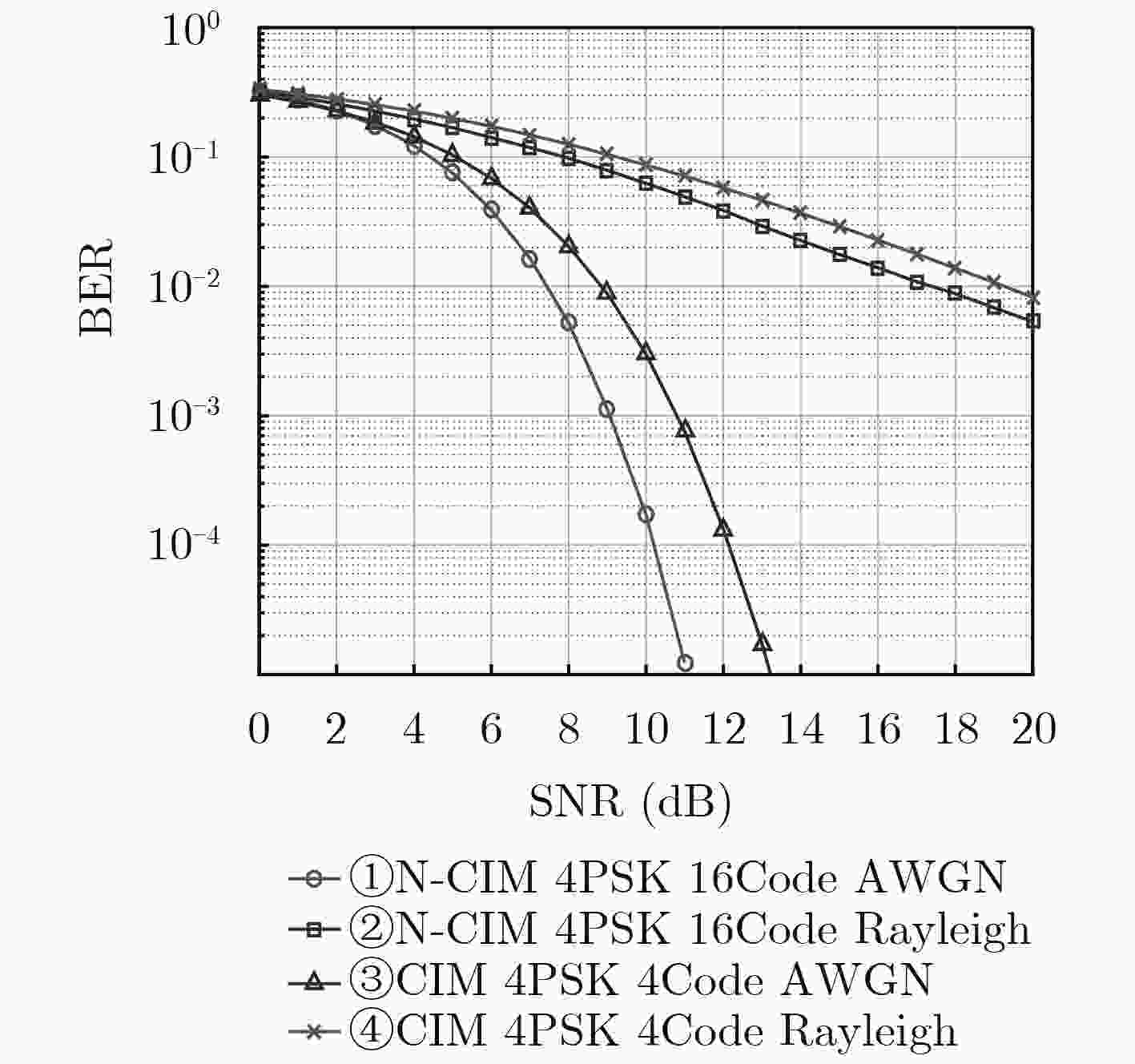
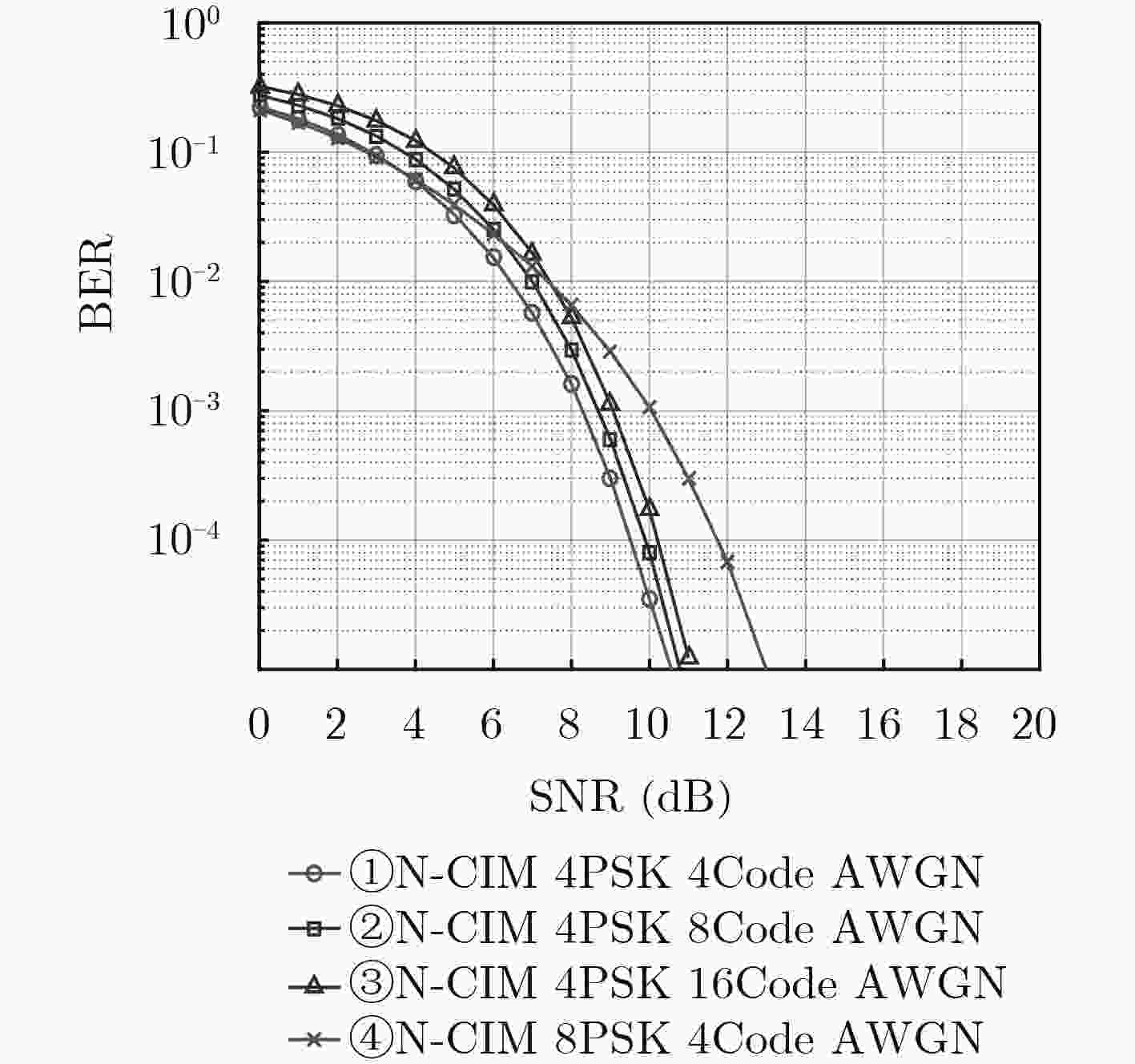
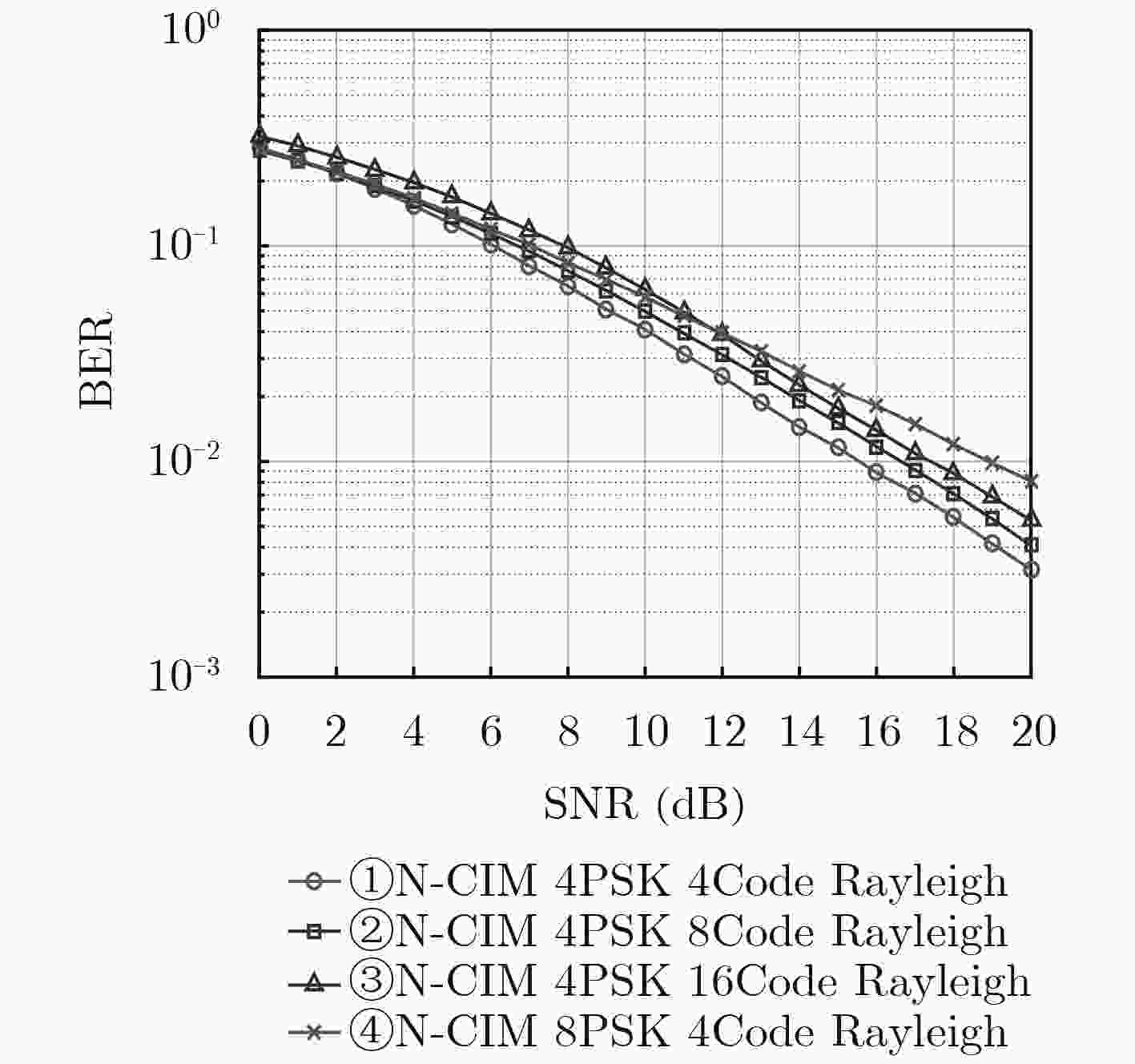
摘要: 针对码索引调制(Code Index Modulation, CIM)相对于直接序列扩频在提升频谱利用率时,造成误比特率性能明显下降的问题,该文提出非正交-码索引调制(Non-orthogonal-Code Index Modulation, N-CIM)。发射端信息比特分割为伪随机(Pseudo Noise, PN)码映射块和调制信息块,并分别映射为PN码的索引和调制符号,调制符号的实部与虚部再选择相同的激活的PN码进行扩频。仿真与分析结果表明,在相同频谱效率时,N-CIM的误比特率性能比CIM在加性高斯白噪声信道中当误比特率为10–5时具备约2~3 dB的优势,在瑞利衰落信道中当误比特率为10–2时具备约2 dB的优势。Abstract: To deal with the problem that the bit error rate reduces obviously when the Code Index Modulation (CIM) is used to improve spectrum utilization, a novel Non-orthogonal-Code Index Modulation (N-CIM) is proposed. The bit stream of the transmitter is divided into mapping block of Pseudo Noise (PN) code and informational block of modulation, which are mapped into the index of the PN code and modulation symbol respectively. The real part and imaginary part of the modulation symbol are spread by selecting the identical activate PN code. Simulation and analysis results show that N-CIM outperforms CIM by about 2~3 dB in additive white Gaussian noise channel when the bit error rate is 10–5, and N-CIM outperforms CIM by about 2 dB in Rayleigh fading channel when the bit error rate is 10–2 at the same spectral efficiency.
-
表 1 PN码索引表
PN码映射块( ${{{d}}_{s,i}}$ )

PN码索引(编号) 000 ${{{w}}_1}$ 

001 ${{{w}}_2}$ 

010 ${{{w}}_3}$ 

011 ${{{w}}_4}$ 

100 ${{{w}}_{\rm{5}}}$ 

101 ${{{w}}_{\rm{6}}}$ 

110 ${{{w}}_{\rm{7}}}$ 

111 ${{{w}}_{\rm{8}}}$ 

-
田日才, 迟永钢. 扩频通信[M]. 第2版, 北京: 清华大学出版社, 2014: 1–5.TIAN Ricai and CHI Yonggang. Spread Spectrum Communication[M]. 2nd Ed., Beijing: Tsinghua University Press, 2014: 1–5. 王玲. 基于Simulink的直接序列扩频通信系统抗干扰的仿真实现[J]. 中国传媒大学学报(自然科学版), 2015, 22(6): 21–27 doi: 10.16196/j.cnki.issn.1673-4793.2015.06.002WANG Ling. Simulation of interference suppression of direct spread spectrum communication system based on simulink[J]. Journal of Communication University of China Science and Technology, 2015, 22(6): 21–27 doi: 10.16196/j.cnki.issn.1673-4793.2015.06.002 BASAR E. Index modulation techniques for 5G wireless networks[J]. IEEE Communications Magazine, 2016, 54(7): 168–175 doi: 10.1109/MCOM.2016.7509396 DATTA T, ESHWARAIAH H S, and CHOCKALINGAM A. Generalized space and frequency index modulation[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 4911–4924 doi: 10.1109/TVT.2015.2451095 BASAR E. On multiple-input multiple-output OFDM with index modulation for next generation wireless networks[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3868–3878 doi: 10.1109/TSP.2016.2551687 付江志, 郭黎利, 杨红乔. 基于复合序列的多进制正交扩频系统性能分析[J]. 系统工程与电子技术, 2010, 32(4): 703–706FU Jiangzhi, GUO Lili, and YANG Hongqiao. Performances of m-ary orthogonal code spread spectrum system based on composite sequences[J]. Systems Engineering and Electronics, 2010, 32(4): 703–706 夏高峰, 罗宇, 金哲仕. 多进制直接序列扩频系统性能分析及仿真[J]. 航空电子技术, 2015, 46(2): 12–15 doi: 10.3969/j.issn.1006-141X.2015.02.06XIA Gaofeng, LUO Yu, and JIN Zheshi. Performance analysis and simulation of m-ary direct sequence spread spectrum system[J]. Avionics Technology, 2015, 46(2): 12–15 doi: 10.3969/j.issn.1006-141X.2015.02.06 郭淑霞, 董文华, 张磊, 等. 混合混沌多进制扩频系统的蒙特卡罗分析[J]. 北京理工大学学报, 2016, 36(7): 760–764 doi: 10.15918/j.tbit1001-0645.2016.07.019GUO Shuxia, DONG Wenhua, ZHANG Lei, et al. Monte carlo analysis of mixed chaotic m-ary direct sequence spread spectrun system[J]. Transaction of Beijing Institute of Technology, 2016, 36(7): 760–764 doi: 10.15918/j.tbit1001-0645.2016.07.019 郭黎利, 姜晓斐, 窦峥. 并行组合扩频超宽带通信系统建模与仿真[J]. 哈尔滨工程大学学报, 2011, 32(4): 499–503 doi: 10.3969/j.issn.1006-7043.2011.04.018GUO Lili, JIANG Xiaofei, and DOU Zheng. Modeling of a UWB communication system based on a parallel combinatory spread spectrum and its simulation analysis[J]. Journal of Harbin Engineering University, 2011, 32(4): 499–503 doi: 10.3969/j.issn.1006-7043.2011.04.018 李北明, 王俊, 薛伟, 等. 基于循环映射算法的并行组合扩频通信[J]. 系统工程与电子技术, 2016, 38(7): 1654–1659 doi: 10.3969/j.issn.1001-506X.2016.07.27LI Beiming, WANG Jun, XUE Wei, et al. Parallel combinatory sapread apectrum communication system with cyclic mapping algorithm[J]. Systems Engineering and Electronics, 2016, 38(7): 1654–1659 doi: 10.3969/j.issn.1001-506X.2016.07.27 LIU Mingduo, QU Zhaowei, and GUO Lili. Improved parallel combinatory spread spectrum communication system[C]. International Computer Conference on Wavelet Active Media Technology and Information Processing, Chengdu, China, 2016: 277–280. QI Lin, GUO Lili, and JIANG Xiaofei. Performance studies of UWB communication system based on parallel combinatory spread spectrum[C]. International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 2009: 1–4. KADDOUM G, AHMED M F A, and NIJSURE Y. Code index modulation: A high data rate and energy efficient communication system[J]. IEEE Communications Letters, 2015, 19(2): 175–178 doi: 10.1109/LCOMM.2014.2385054 KADDOUM G and SOUJERI E. On the comparison between code index modulation and spatial modulation techniques[C]. 2015 IEEE International Conference on Information and Communication Technology Research, Abu Dhabi, United Arab Emirates, 2015: 24–27. KADDOUM G, NIJSURE Y, and TRAN H. Generalized code index modulation technique for high data rate communication systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7000–7009 doi: 10.1109/TVT.2015.2498040 -





 下载:
下载:


 下载:
下载:
