Modified MUSIC Algorithm for Multiple Measurement Vector Models
-
摘要: 压缩感知多测量向量(MMV)模型用于解决具有相同稀疏结构的多快拍问题，在传统阵列信号处理应用中多重信号分类(MUSIC)方法是一种常见的方法，但当快拍数不足(低于稀疏度)时其性能将急剧恶化。Kim等人(2012)推导出一种修正的MUSIC谱，并将压缩重构方法和MUSIC算法结合提出压缩感知MUSIC算法(CS-MUSIC)，能够有效克服快拍数不足的问题。该文将Kim等人的结论扩展到一般情形，并基于传统的MUSIC谱和CS-MUSIC谱提出一种修正的MUSIC算法(MMUSIC)。仿真结果表明所提算法能够有效克服快拍数不足的问题，并且具有比CS-MUSIC算法和压缩感知贪婪算法更高的重构概率。Abstract: The Compressed Sensing (CS) Multiple Measurement Vector (MMV) model is used to solve multiple snapshots problem with the same sparse structure. MUltiple SIgnal Classification (MUSIC) is a common method in traditional array signal processing applications. However, when the number of snapshots is below sparsity performance will be dramatically deteriorated. Kim et al. derive a modified MUSIC spectral method and propose a Compressed Sensing MUSIC method (CS-MUSIC) combining the compression reconstruction method and the MUSIC algorithm, which can effectively overcome the problem of insufficient snapshot number. In this paper, Kim et al.’s conclusion is extended to the general case, and a Modified MUSIC (MMUSIC) algorithm is proposed based on the traditional MUSIC method and the CS-MUSIC method. The simulation results show that the proposed algorithm can effectively overcome the shortage of snapshots and has a higher reconstruction probability than the CS-MUSIC algorithm and the compressed sensing greedy algorithm.
-
CANDÈS E J and TAO T. Near-optimal signal recovery from random projections: Universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406–5425 doi: 10.1109/TIT.2006.885507 DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306 doi: 10.1109/TIT.2006.871582 CANDÉS E J, ROMBERG J, and TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 53(2): 489–509 doi: 10.1109/TIT.2005.862083 BLANCHARD J D, CERMAK M, HANLE D, et al. Greedy algorithms for joint sparse recovery[J]. IEEE Transactions on Signal Processing, 2014, 62(7): 1694–1704 doi: 10.1109/TSP.2014.2301980 CHOI J W, SHIM B, and DING Y. Compressed sensing for wireless communications: Useful tips and tricks[J]. IEEE Communications Surveys and Tutorials, 2017, 19(3): 1527–1550 doi: 10.1109/COMST.2017.2664421 GUO Jie, SONG Bin, and HE Ying. A survey on compressed sensing in vehicular infotainment systems[J]. IEEE Communications Surveys and Tutorials, 2017, 19(4): 2662–2680 doi: 10.1109/COMST.2017.2705027 YANG Lin, SONG Kun, and SIU Yunming. Iterative clipping noise recovery of ofdm signals based on compressed sensing[J]. IEEE Transactions on Broadcasting, 2017, 63(4): 706–713 doi: 10.1109/TBC.2017.2669641 DU Zhaohui, CHEN Xuefeng, ZHANG Han, et al. Compressed-Sensing-based periodic impulsive feature detection for wind turbine systems[J]. IEEE Transactions on Industrial Informatics, 2017, 12(6): 2933–2945 doi: 10.1109/TII.2017.2666840 WU Kai and LIU Jing. Learning large-scale fuzzy cognitive maps based on compressed sensing and application in reconstructing gene regulatory networks[J]. IEEE Transactions on Fuzzy Systems, 2017, 25(6): 1546–1560 doi: 10.1109/TFUZZ.2017.2741444 石要武, 陈淼, 单泽涛, 等. 基于特征空间MUSIC算法的相干信号波达方向空间平滑估计[J]. 吉林大学学报(工学版), 2017, 47(1): 268–273 doi: 10.13229/j.cnki.jdxbgxb201701039SHI Yaowu, CHEN Miao, SHAN Zetao, et al. Spatial smoothing technique for coherent signal DOA estimation based on eigen space MUSIC algorithm[J]. Journal of Jilin University(Engineering and Technology Edition) , 2017, 47(1): 268–273 doi: 10.13229/j.cnki.jdxbgxb201701039 COTTER S F, RAO B D, ENGAN K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Transaction on Signal Processing, 2005, 53(7): 2477–2488 doi: 10.1109/TSP.2005.849172 BRESLER Y. Spectrum-blind sampling and compressive sensing for continuous-index signals[C]. Information Theory and Applications Workshop, San Diego, USA, 2008: 547–554. SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280 doi: 10.1109/TAP.1986.1143830 KIM J M, LEE O K, and YE J C. Compressive MUSIC: revisiting the link between compressive sensing and array signal processing[J]. IEEE Transactions on Information Theory, 2012, 58(1): 278–301 doi: 10.1109/TIT.2011.2171529 吕志丰, 雷宏. 基于差值映射的压缩感知MUSIC算法[J]. 电子与信息学报, 2015, 37(8): 1874–1878 doi: 10.11999/JEIT141542LÜ Zhifeng and LEI Hong. Compressive sensing MUSIC algorithm based on difference map[J]. Journal of Electronics&Information Technology, 2015, 37(8): 1874–1878 doi: 10.11999/JEIT141542 TROPP J A. Algorithms for simultaneous sparse approximation. Part II: convex relaxation[J]. Signal Processing, 2006, 86(3): 589–602 doi: 10.1109/TSP.2016.2637314 WIPF D P and RAO B D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Transaction on Signal Processing, 2007, 55(7): 3704–3716 doi: 10.1109/TSP.2007.894265 BARANIUK R G, CEVHER V, DUARTE M F, et al. Model-based compressive sensing[J]. IEEE Transactions on Information Theory, 2010, 56(4): 1982–2001 doi: 10.1109/TIT.2010.2040894 -
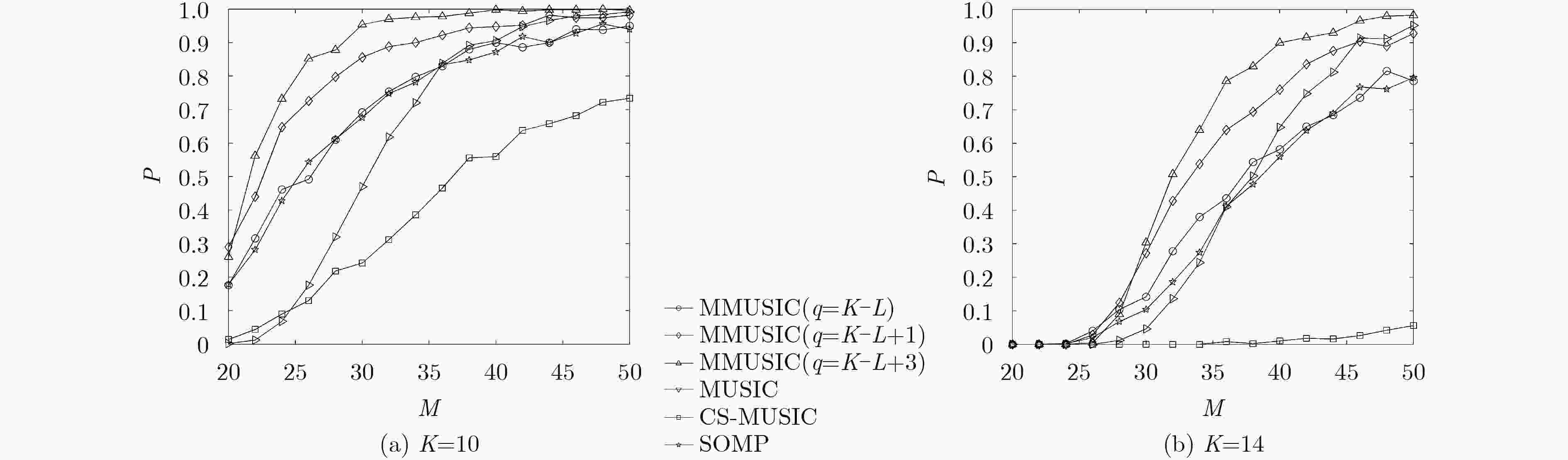
下载:
图(3)
计量
- 文章访问数: 1541
- HTML全文浏览量: 548
- PDF下载量: 74
- 被引次数: 0
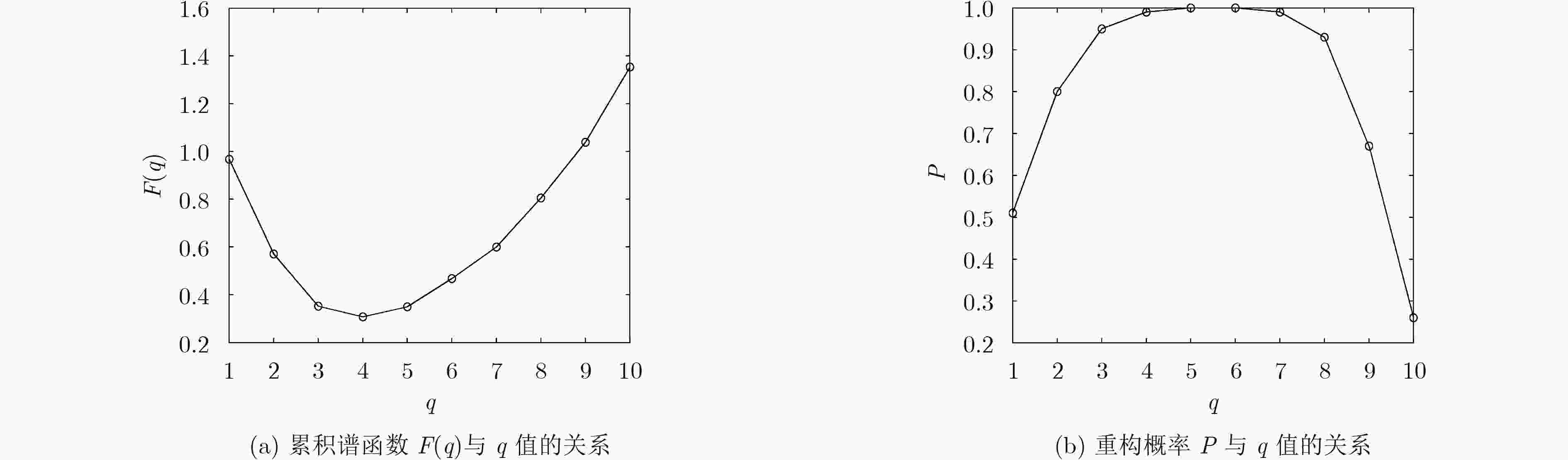
下载:
