Anti-interrupted Sampling Repeater Jamming Waveform Design Method
-
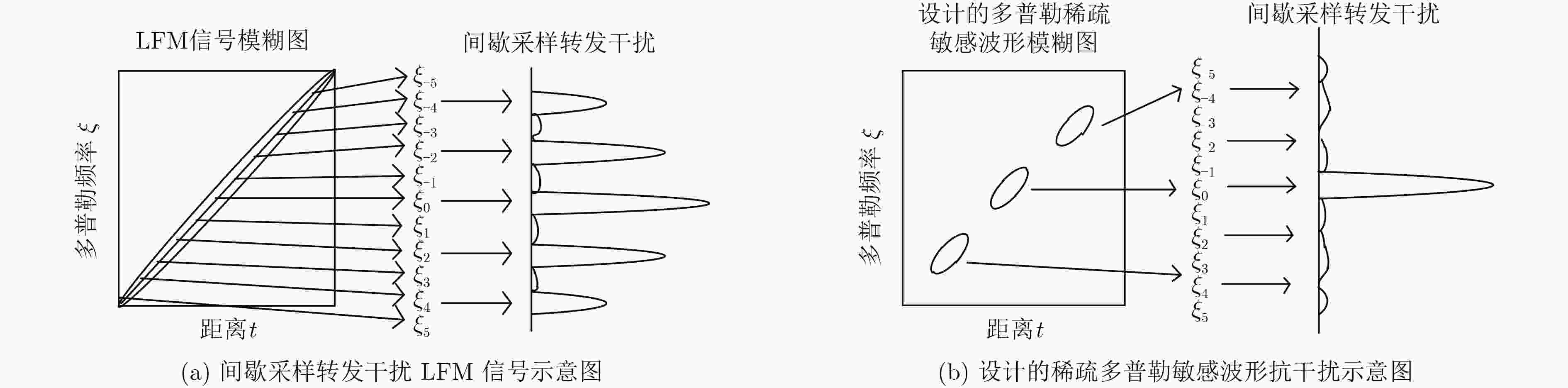
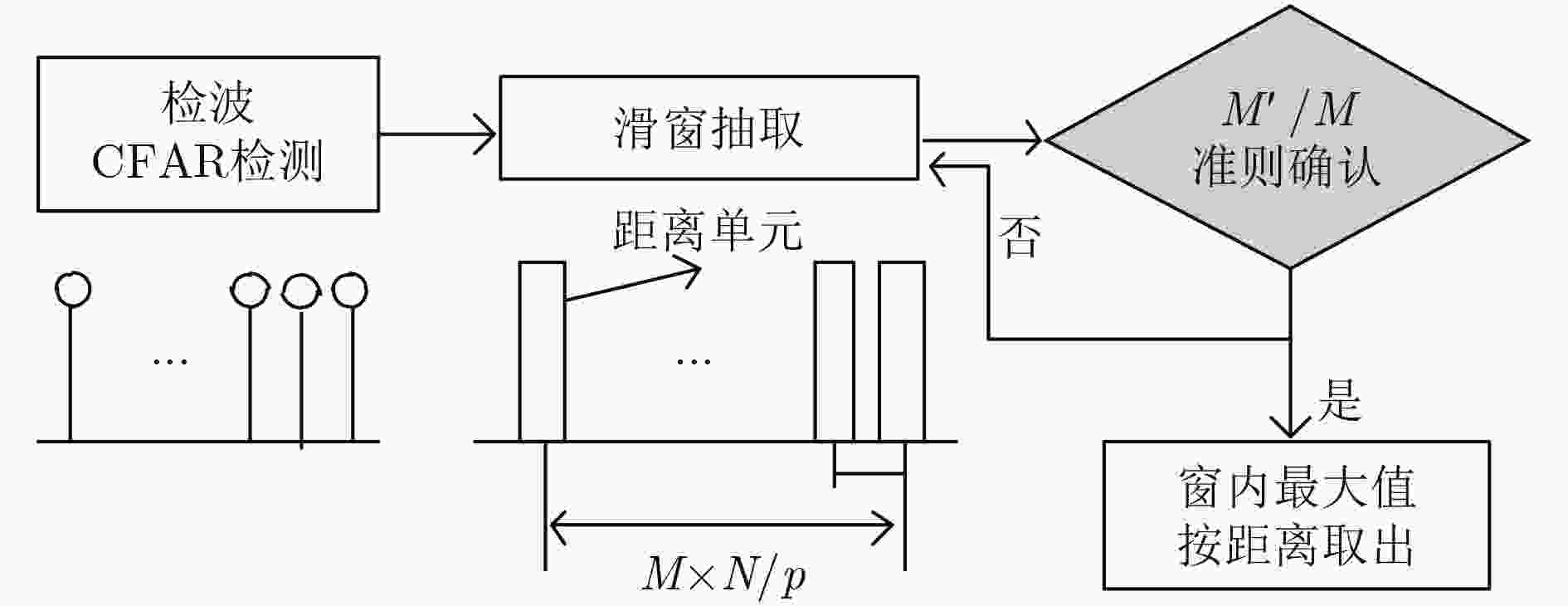
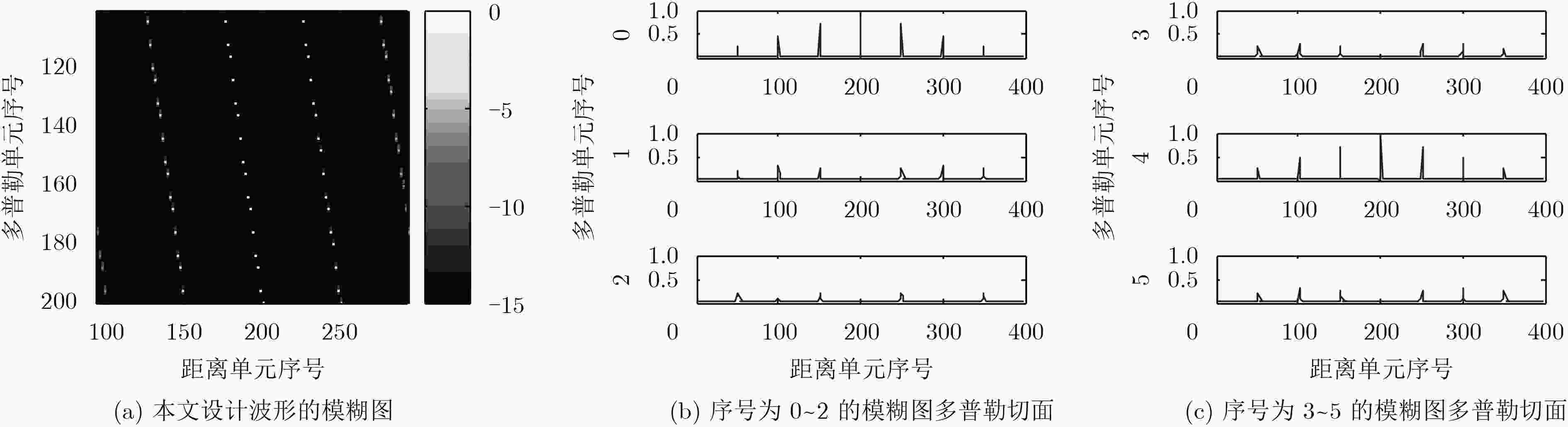
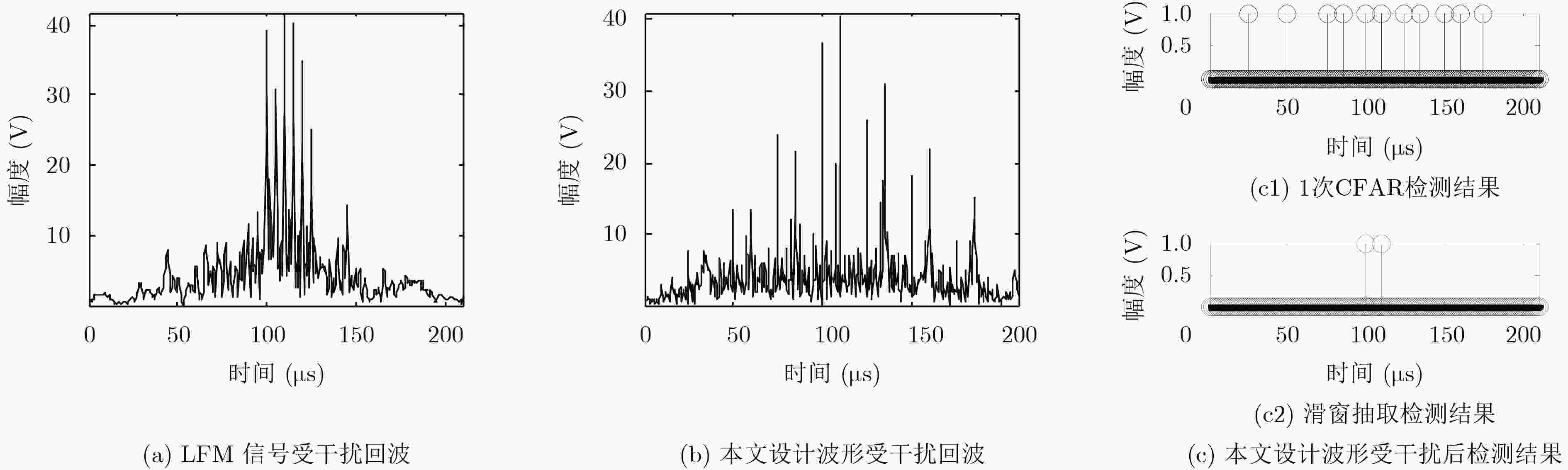
摘要: 间歇采样转发干扰是一种先进的密集假目标干扰技术,该技术基于“欠采样”原理对雷达信号进行低速率间歇采样处理,具有干扰快速响应、抗捷变能力强等优点,能够使雷达无法检测真实目标,甚至使信号处理系统过载。该文针对间歇采样转发干扰样式,基于模糊函数理论,首先设计了一种抑制该干扰的特殊雷达工作波形,即“稀疏多普勒敏感波形”,这种波形通过破坏干扰信号多普勒频率上的输出连续性实现对干扰信号的抑制;然后,基于该波形在时域上的等间隔副瓣特性,提出一种时域上的“滑窗抽取检测”方法,在抗干扰的同时实现目标检测;最后,理论分析和仿真实验验证了该设计波形的干扰抑制有效性,以及“滑窗抽取检测”方法在干扰背景下的良好目标检测性能。Abstract: Interrupted Sampling Repeater Jamming (ISRJ) is an advanced intensive false-target jamming with the advantages of fast interference response, anti-agile ability and so on. The radar signal is intermittently sampled with low-rate based on the principle of the under-sampling method, so that the radar can not detect the real targets and the jamming may overload the signal processing system. This article mainly focuses on the Interrupted Sampling Repeater Jamming. A sensitive Doppler sparse waveform is designed based on the ambiguity function theory to suppress the interference, which destroys the continuity of the interference signal output on different Doppler and suppresses the output of the intensive interference. Based on the analysis of the equivalent interval sidelobe, a method of sliding window extraction detection is proposed to achieve effective target detection while anti-jamming. Theoretical analysis and simulation experiments demonstrate the effectiveness of the interference suppression and the target detection performance in the interference.
-
表 1 仿真实验参数
参数 实验值 参数 实验值 脉冲宽度T 100 μs 信号带宽B 1 MHz 干扰采样周期 ${T_J}$ 20 μs 占空比 0.2 采样频率 ${f_s}$ 2 MHz 采样点数 200 -
王雪松, 刘建成, 张文明, 等. 间歇采样转发干扰的数学原理[J]. 中国科学, 2006, 36(8): 891–901 doi: 10.3969/j.issn.1674-7259.2006.08.007WANG Xuesong, LIU Jiancheng, ZHANG Wenming, et al. The mathematical principle of Interrupted Sampling Repeater Jamming[J]. Science in China Series E Information Sciences, 2006, 36(8): 891–901 doi: 10.3969/j.issn.1674-7259.2006.08.007 SPARROW M J and CIKALO J. ECM techniques to counter pulse compression radar[P]. US Patent 7081846, 2006. 马晓峰, 陆乐, 盛卫星, 等. 干扰子空间正交投影快速零陷跟踪波束赋形算法[J]. 电子与信息学报, 2016, 38(10): 2560–2567 doi: 10.11999/JEIT151438MA Xiaofeng, LU Le, SHENG Weixing, et al. Fast nulls tracking pattern synthesis based on jammer subspace orthogonal projection[J]. Journal of Electronics&Information Technology, 2016, 38(10): 2560–2567 doi: 10.11999/JEIT151438 GANG Lu and BIN Tang. Deception jammer rejection using pulse diversity in joint slow/fast-time domain[J]. Journal-Chinese Institute of Engineers, 2013, 36(3): 405–410 doi: 10.1080/02533839.2012.731847 HAYKIN S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazin, 2006, 23(1): 30–40 doi: 10.1109/MSP.2006.1593335 YU Xianxiang, CUI Guolong, GE Peng, et al. Constrained radar waveform design algorithm for spectral coexistence[J]. Electronics Letters, 2017, 53(8): 558–560 doi: 10.1049/el.2016.4524 FENG Xiang, SONG Yangchun, ZHOU Zhiquan, et al. Designing unimodular waveform with low range sidelobes and stopband for cognitive radar via relaxed alternating projection[J]. International Journal of Antennas and Propagation, 2016, 2016: 1–9 doi: 10.1155/2016/6280508 HE Hao. Waveform design for active sensing systems: A computational approach[D]. [Ph.D. dissertation], Cambridge University Press, UK, 2012. 冯翔, 陈志坤, 赵宜楠, 等. 基于联合优化松弛交替投影的组网雷达恒模波形设计方法[J]. 电子与信息学报, 2016, 38(7): 1745–1751 doi: 10.11999/JEIT151152FENG Xiang, CHEN Zhikun, ZHAO Yinan, et al. Unimodular waveforms design for netted radar system via joint optimization relaxed alternating projectio[J]. Journal of Electronics&Information Technology, 2016, 38(7): 1745–1751 doi: 10.11999/JEIT151152 李玉翔, 任修坤, 孙扬, 等. 一种循环迭代的宽带MIMO雷达正交稀疏频谱波形设计方法[J]. 电子与信息学报, 2017, 39(4): 953–959 doi: 10.11999/JEIT160597LI Yuxiang, REN Xiukun, SUN Yang, et al. Cyclic iterative method for wideband MIMO radar orthogonal sparse frequency waveform design[J]. Journal of Electronics&Information Technology, 2017, 39(4): 953–959 doi: 10.11999/JEIT160597 PETER S, HE Hao, and LI Jian. New algorithms for designing unimodular sequences with good correlation properties[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1415–1425 doi: 10.1109/TSP.2009.2012562 SONG Junxiao, PRABDU B, and DANIEL P. Sequence design to minimize the weighted integrated and peak sidelobe levels[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2051–2064 doi: 10.1109/TSP.2015.2510982 ANTONIO D M, HUANG Y, PIEZZO M, et al. Design of optimized radar codes with a peak to average power ratio constraint[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2683–2697 doi: 10.1109/TSP.2011.2128313 SOLTANALIAN M and STOICA P. Designing unimodular codes via quadratic optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(5): 1221–1234 doi: 10.1109/TSP.2013.2296883 EUSTICE D, BAYLIS C, LATHAM C, et al. Optimizing radar waveforms using generalized alternating projections[C]. Wireless & Microwave Circuits & Systems, Waco Texas, 2015: 1–6. ZHANG Jingdong, QIU Xiaoyan, SHI Changli, et al. Cognitive radar ambiguity function optimization for unimodular sequence[J]. EURASIP Journal on Advances in Signal Processing, 2016, 2016(31): 1–13 doi: 10.1186/13634-016-0325-3 WU L L, BADU P, and DANIEL P. Cognitive radar-based sequence design via SINR maxmization[J]. IEEE Transactions on Signal Processing, 2017, 65(3): 779–793 doi: 10.1109/TSP.2016.2621723 AUBRY A, DE Maio A, JIANG B, et al. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]. IEEE Transactions on Signal Processing, 2013, 61(22): 5603–5619 doi: 10.1109/TSP.2013.2273885 RICHARDS M A. Fundamentals of Radar Signal Processing[M]. New York: McGraw-Hill, 2014: 139–147. 李秀友, 关键, 薛永华, 等. 模糊函数约束下的高多普勒容忍性波形设计方法[J]. 信号处理, 2015, 31(12): 1612–1618 doi: 10.3969/j.issn.1003-0530.2015.12.011LI Xiuyou, GUAN Jian, XUE Yonghua, et al. High Doppler tolerance waveform design method constrained by ambiguity function[J]. Journal of Signal Processing, 2015, 31(12): 1612–1618 doi: 10.3969/j.issn.1003-0530.2015.12.011 -






 下载:
下载:




 下载:
下载:
