Multiple to One Fully Homomorphic Encryption Scheme over the Integers
-
摘要: 全同态加密是在不解密密文的情况下直接对密文进行操作。现有的基于整数的全同态加密方案是针对两个参与者“一方加密,一方解密”(一对一)设计的,计算效率普遍低,明文空间小,不能应用于大数据、云计算等环境。为此,该文提出一种“多方加密,一方解密”(多对一)的全同态加密方案,该方案在保证安全性的基础上简化密钥生成过程,并在全同态运算过程中给出能够正确解密的加密方个数的具体范围。同时,在随机预言机模型下,基于近似最大公因子问题证明了方案的安全性。数值结果表明,该方案与已有方案相比不仅扩展了数据传输量,而且提高了效率。模拟实验表明,该方案在整数范围内具有可行性,满足用户对系统响应的需求,最后将明文空间扩展为3 bit,并与1 bit的方案做出了实验上的对比分析。Abstract: Fully homomorphic encryption allows any operation evaluation on encrypted data without decryption. The existing integer-based homomorphic encryption schemes are designed only for two participants namely one party encryption one party decryption (one-to-one), whose computational efficiency is generally low, plaintext space is small, so it can not be applied to big data, cloud computing and other actual scene. Therefore, a full homomorphic encryption scheme with multi-party encryption, one party decryption (multiple to one) is presented. The scheme simplifies the key generation process on the basis of guaranteeing the security, but also gives the range of the number of encrypted parties that can be decrypted accurately in the process of homomorphic operation. Meanwhile, in the random oracle model, the security of the new scheme is proved based on approximate Greatest Common Divisor (GCD) problem. Numerical analysis demonstrates that the presented scheme can not only extend the data traffic, but also improve the efficiency by comparing with the existing schemes. Simulation results show that proposed scheme is more practical in the range of integer, and meets the requirements of the users to the system response. Finally, the plaintext space is expanded to 3 bit, comparing and analysing the experiment with the scheme of 1 bit.
-
表 1 方案的安全性、效率和加\解密的参与者比较
方案名称 文献[3] 文献[13] 本文方案 安全级别 IND-CPA IND-CPA IND-CPA 连续性 好 好 好 困难问题 近似最大公因子问题 近似最大公因子问题 近似最大公因子问题 公钥尺寸 $\widetilde O\left( {{\lambda ^{10}}} \right)$ $\widetilde O\left( {{\lambda ^7}} \right)$ $\widetilde O\left( {{\lambda ^{10}}} \right)$ 私钥尺寸 $\widetilde O\left( {{\lambda ^2}} \right)$ $\widetilde O\left( {{\lambda ^2}} \right)$ $\widetilde O\left( {{\lambda ^2}} \right)$ 单次传输数据量 1 bit 3 bit $l$ bit 加/解密的参与者 一对一 一对一 多对一 表 2 实验环境配置
计算机型号 操作系统 处理器 内存 开发环境 运算库 数据处理 HP Compad 8280 Elite Windows 7(32位) Inter Core i5~2400M (3.10 GHz) 4 GB Visual C++ 6.0 PBC-0.4.7-VC MATLAB 2010 -
RIVEST R. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the ACM, 1978, 21(2): 120–126 doi: 10.1145/357980.358017 GENTRY C. Fully homomorphic encryption using ideal lattices[C]. ACM Symposium on Theory of Computing, Bethesda, USA, 2009: 169–178. DIJK M, GENTRY C, HALEVI S, et al. Fully homomorphic encryption over the integers[C]. International Conference on the Theory and Applications of Cryptographic Techniques, Berlin, Heidelberg, 2010: 24–43. STEHLE D and STEINFELD R. Faster fully homomorphic encryption[C]. Advances in Cryptology-ASIACRYPT 2010, International Conference on the Theory and Application of Cryptology and Information Security, Singapore, 2010: 377–394. GENTRY C and HALEVI S. Implementing Gentry’s fully-homomorphic encryption scheme[C]. Advances in Cryptology-EUROCRYPT 2011, International Conference on the Theory and Applications of Cryptographic Techniques, Tallinn, Estonia, 2011: 129–148. SMART N and VERCAUTEREN F. Fully homomorphic encryption with relatively small Key and ciphertext sizes[C]. International Conference on Practice and Theory in Public Key Cryptography, Paris, France, 2010: 420–443. CHENAL M and TAHG Q. On key recovery attacks against existing somewhat homomorphic encryption schemes[J]. Lecture Notes in Computer Science, 2014, 8895: 239–258 doi: 10.1007/978-3-319-16295-9_13 TANG Dianhua and ZHU Shixiong. Faster fully homomorphic encryption scheme over integer[J]. Computer Engineering&Applications, 2012, 48(28): 117–122 doi: 10.3778/j.issn.1002-8331.2012.28.023 GU Chunsheng, JING Zhengjun, YU Zhimin et al. Breaking faster fully homomorphic encryption scheme over integer[J]. Computer Engineering&Applications, 2013, 49(21): 101–105 doi: 10.3778/j.issn.1002-8331.1201-0401 光焱, 顾纯祥, 祝跃飞, 等. 一种基于LWE问题的无证书全同态加密体制[J]. 电子与信息学报, 2013, 35(4): 988–993 doi: 10.3724/SP.J.1146.2012.01102GUANG Yan, GU Chunxiang, ZHU Yuefei, et al. Certificateless fully homomorphic encryption based on LWE problem[J]. Journal of Electronics&Information Technology, 2013, 35(4): 988–993 doi: 10.3724/SP.J.1146.2012.01102 古春生. 近似理想格上的全同态加密方案[J]. 软件学报, 2015, 26(10): 2696–2719 doi: 10.13328/j.cnki.jos.004808Gu Chunsheng. Fully homomorphic encryption from approximate ideal lattices[J]. Journal of Software, 2015, 26(10): 2696–2719 doi: 10.13328/j.cnki.jos.004808 熊婉君, 韦永壮, 王会勇. 一个基于整数的全同态加密改进方案[J]. 密码学报, 2016, 3(1): 67–78 doi: 10.13868/j.cnki.jcr.000110XIONG Wanjun, WEI Yongzhuang, and WANG Huiyong. An improved fully homomorphic encryption scheme over the integers[J]. Journal of Cryptologic Research, 2016, 3(1): 67–78 doi: 10.13868/j.cnki.jcr.000110 HU Renyuan, ZHANG Longjun, and QIN Yongzhen. Improved fully homomorphic encryption algorithm for cloud storage[C]. International Conference on Communications, Information Management and Network Security, Shanghai, China, 2016: 349–352. 夏超.同态加密技术及其应用研究[D]. [硕士论文], 安徽大学, 2013.XIA Chao. Research of homomorphic encryption technolosgy and application[D]. [Master dissertation], Anhui University, 2013. -





 下载:
下载:
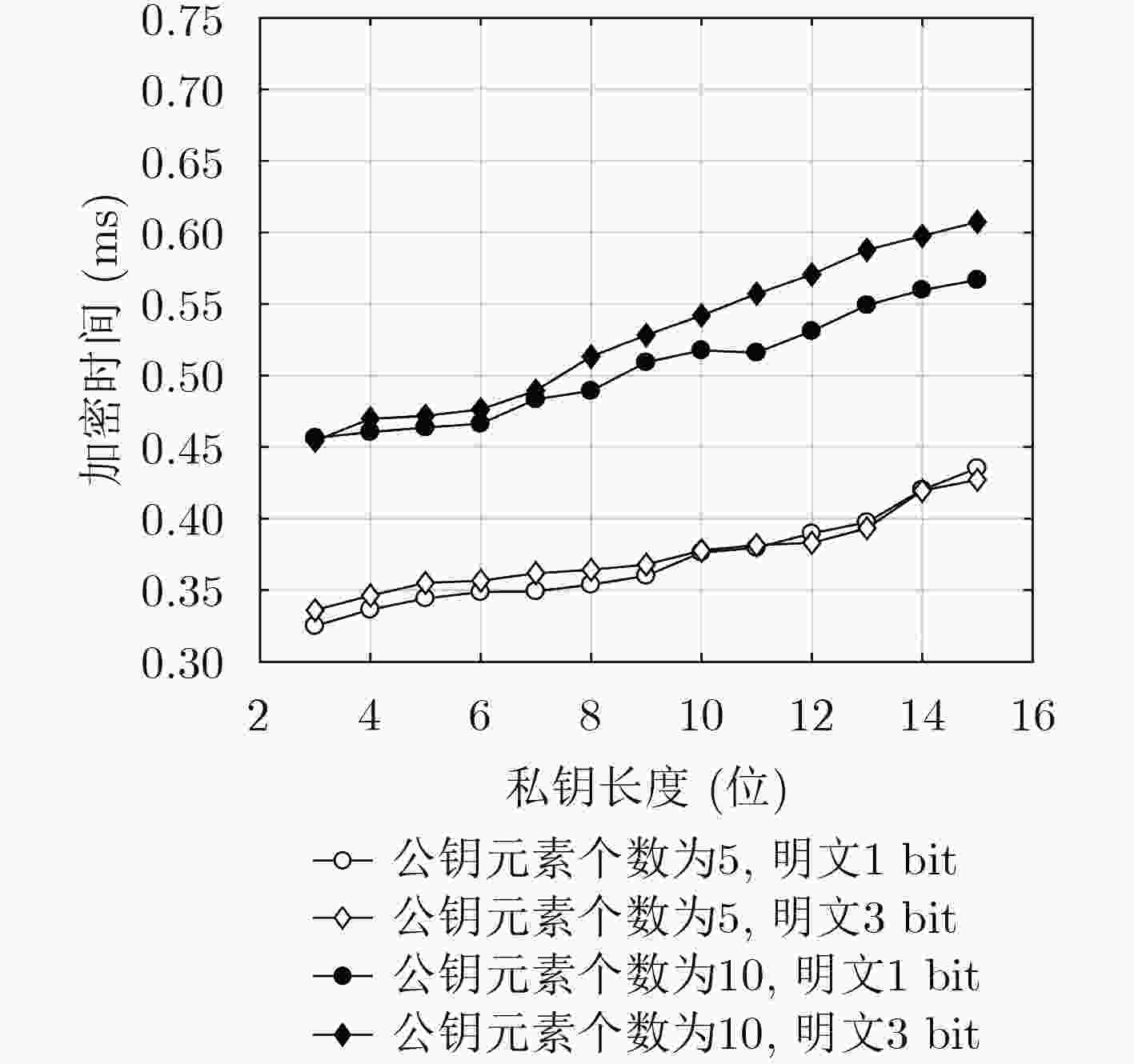
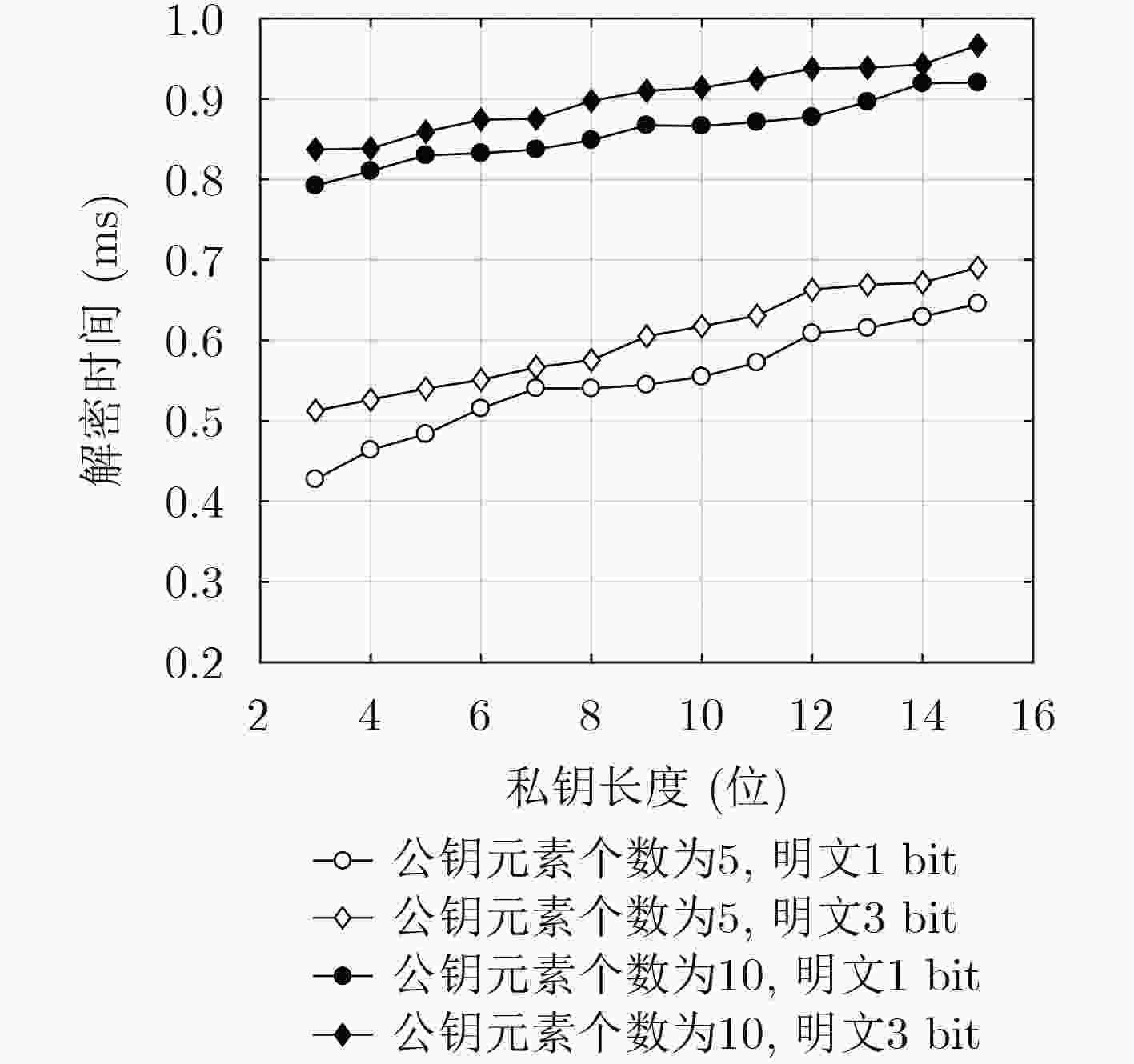


 下载:
下载:
