Research of Discrimination Between Left and Right Hand Motor Imagery EEG Patterns Based on Tunable Q-Factor Wavelet Transform
-
摘要:
针对识别左右手运动想象脑电图信号(EEG)模式精度和互信息不高的问题，该文采用基于可调Q因子小波变换(TQWT)算法来处理脑电信号。首先，利用TQWT对脑电图信号进行分解；随后，提取子频带信号的小波系数能量、自回归模型(AR)系数以及分形维数；最后，利用线性判别分析(LDA)对提取的脑电特征进行识别。采用BCI2003和BCI2005竞赛数据对所提出的算法进行验证，4名受试者的最高识别率分别为88.11%, 89.33%, 77.13%和78.80%，最大互信息分别为0.95, 0.96, 0.43和0.45。实验结果表明，所提算法取得了高分类精度及互信息值，验证了其有效性。
Abstract:In view of the problem of low accuracy and mutual information in left and right hand motor imagery-based ElectroEncephaloGram (EEG), a new approach based on Tunable Q-factor Wavelet Transform (TQWT) is proposed to handle with the binary-class motor imagery EEGs. Firstly, the TQWT is utilized to decompose the filtered EEG signal. Then, several sub-band signals are extracted and followed by calculating their energy, AutoRegressive (AR) model coefficients and fractal dimension. Finally, a Linear Discriminant Analysis (LDA) classifier is used to classify these EEGs. Two Graz datasets of BCI Competition 2003 and 2005 are employed to verify the proposed method. The maximum accuracy of classifying EEGs of four subjects is 88.11%, 89.33%, 77.13% and 78.80%, respectively, and the maximum mutual information is 0.95, 0.96, 0.43 and 0.45. The high accuracies and mutual information demonstrate eventually the effectiveness of the proposed method.
-
1. 引言
脑-机接口(Brain-Computer Interface, BCI)是一种不依赖于大脑正常输出通路(即外围神经和肌肉组织)就可以实现人脑与外界(计算机或其它外部装置)直接通信的人-机接口[1]。运动想象是能够人为控制的意念活动。当人进行单侧肢体运动想象任务时，对侧大脑感觉运动皮层处于激活状态，相应节律的信号幅值会下降，这种现象称为事件相关去同步(Event-Related Desynchronization, ERD)；而同侧大脑皮层处于阻滞状态，相应节律的信号幅值会上升，这种现象称为事件相关同步(Event-Related Synchronization, ERS)[2]。根据ERS/ERD现象能够实现对运动想象脑电信号的分类[3]。
脑电信号是一种不具备各态历经性的非线性、非平稳随机信号[4]，传统的信号处理方法如：快速傅里叶变换(Fast Fourier Transform, FFT)、短时傅里叶变换(Short-Time Fourier Transform, STFT)、幅频分析[5]等，虽然能在频域内对信号进行准确高效的分析，但在时域缺少分辨能力。而小波变换能够同时在时域和频域进行表现，对于时变信号可以非常方便地进行时域和频域的往返变换。小波相关方法在运动想象脑电信号的特征提取领域应用十分广泛。Hamid等人[6]利用离散小波变换方法，同时应用基于环拓扑的粒子群优化算法，对左右手运动想象脑电信号进行分类，取得了82.91%的平均识别率；Pattnaik等人[7]将离散小波变换方法和人工神经网络分类器结合，对左右手运动想象脑电信号进行分类，取得了80.71%的最高识别率；徐佳琳等人[8]利用连续小波变换、小波包分解等特征提取算法进行特征选择并与主成分分析算法对比，实现了较好的降维效果。近几年，双树复小波变换[9]、双密度小波变换[10]等方法也开始应用于脑电信号的识别。
虽然和傅里叶变换相比，小波变换方法具有显著优势，但对信号进行小波变换时，需选定合适的小波基函数，而采用单个基函数推出的小波函数难以在不同尺度上准确地逼近信号局部特征，因此在重构信号时会丢失原有的时域特征[11]。可调Q因子小波变换(Tunable Q-Factor Wavelet Transform, TQWT)是一种完全离散的小波变换方法[12]，非常适用于分析包括脑电信号在内的振荡信号[13]，其参数可以根据信号的振荡特性进行任意调节。在时间尺度域上，TQWT能够可靠地表征信号的稀疏性以及非平稳性。本文提出一种采用TQWT进行分解并选择小波系数能量、AR系数及分形维数作为特征的左右手运动想象脑电特征提取方法并采用线性判别分析(Linear Discriminant Analysis, LDA)进行分类。通过仿真实验，证明了方法的有效性及优异性。将实验结果与近期使用相同数据集的文献[5,6]进行对比，本文方法取得了更高的平均分类准确率和最大互信息。
2. 实验数据和方法
2.1 实验数据
本文所用两类运动想象脑电数据来源于第2届国际脑-机接口竞赛的dataset Ⅲ[14]和第3届国际脑-机接口竞赛的dataset Ⅲb[15]。dataset Ⅲ采用280个试次，信号采样频率为128 Hz，每次试验持续时间为9 s。dataset Ⅲb包含3名受试者试验结果(O3VR, S4和X11), O3VR采用400个试次，S4和X11各采用1080个试次，信号采样频率为125 Hz，每次试验持续时间为8 s。上述每段脑电信号均经过0.5～30.0 Hz滤波处理以获得ERS/ERD现象相关脑电频段[16]。
2.2 实验原理
2.2.1 可调Q因子小波变换
TQWT有3个可调参数，它们分别是品质因子
Q 、过采样率r 和信号分解层数J 。品质因子Q 作为小波振荡次数的度量，其值越大，小波振荡频次越高，反之，小波振荡频次越低；过采样率r 控制过度振铃现象，起到局域化信号特征的作用，通常选择r ≥3[17](在本文中，r 设为3)；信号分解层数J 决定了信号被分解的层数，J 越大，则信号被分解得越细致。与传统小波相同，TQWT也利用了双通道滤波器组和尺度变换实现了离散小波变换[18]。图1所示为4层TQWT信号分解实现过程，其中，ci(n) 和di(n) (i =1, 2, 3, 4)分别代表低通信号和高通信号。在信号分解时，信号S(n) 经过离散傅里叶变换后进行双通道滤波和尺度变换被分解成低通信号成分c1(n) 和高通信号成分d1(n) ,d1(n) 被保留作为本层输出信号，而c1(n) 则作为下一层的输入信号继续进行变换，不断重复此过程直至将有限长信号分解至给定的分解层数为止。在J 层TQWT中，信号ci(n) 和di(n) (i =1, 2, ···,J )的采样频率分别为αfs 和βfs 。其中，α 和β 为尺度参数，fs 为信号S(n) 的采样频率。TQWT的低通滤波器和高通滤波器如式(1)，式(2)[19]：
H0(ω)={1, |ω<(1−β)π|θ(ω+(β−1)πα+β−1),(1−β)π≤|ω|<απ0, απ≤|ω|≤π (1) H1(ω)={0, |ω<(1−β)π|θ(απ−ωα+β−1),(1−β)π≤|ω|<απ1, απ≤|ω|≤π (2) 其中，
θ(ω) 代表具有2阶消失矩的Daubechies频率响应，表达式如式(3)：θ(ω)=0.5(1+cosω)√2−cosω, |ω|≤π (3) 参数
Q 和r 可以通过滤波器参数α 和β 进行计算Q=f0/BW=(2−β)/β (4) r=β/(1−α) (5) 其中，
f0 为振荡中心频率，BW 为带宽，α 和β 满足：α<β≤1 ,0<α<1 ，且α+β>1 。2.2.2 时频-非线性特征提取
在对脑电信号进行特征提取时，先利用TQWT对脑电信号进行分解，随后对分解所得子频带进行特征提取。实验中，为模拟在线识别环境，利用滑动窗提取信号子频带的特征，步骤为：
(1)对所选子频带时间序列，选择长度为3 s的滑动窗，以
t =4 s作为窗体右端点，考虑不同受试者的差异性，为使能够将数据段切割成整数个数据窗，对于第1名受试者，窗口每次滑动距离为0.0625 s，对于第2名到第4名受试者，窗口每次滑动距离为0.04 s，分别将4～8 s内的数据切割成65和101个数据窗；(2)分别计算每个数据段的小波系数能量、AR系数和分形维数共3个参数，组成特征向量。对于单试次数据，假设TQWT分解层数为7, AR阶数为4，对C3, C4两个电极需计算16个小波系数能量参数，8个AR系数参数以及2个分形维数参数，共计26个参数值。
3个特征参数的定义为：
(1)信号的时域能量[20]是一种简单且直接的特征，给定时域信号{
X(t) ,t =0, 1, 2,···,N –1}，其时域能量表达式为E=N−1∑n=0|X(t)|2 (6) (2) AR模型估计[21]假定信号可以用过去时间的信号通过线性组合的方式来表示。一个
n 阶AR模型可以表示为X(t)=n∑t=1a(i)X(t−i)+e(t) (7) 其中，
n 表示t 时刻之前的n 个时间点，e(t) 表示方差为δ2 均值为0的白噪声，系数a(i) (i =1, 2, ···,n )和δ2 为AR模型的参数。本文中，将AR系数a(i) 作为分类器输入参数。(3)分形维数[22]是一种以统计学的角度定义时间序列的复杂程度的非线性特征，它能够揭示隐含在自发脑电信号不规则形状和不稳定性中的特征。其值越大，表明复杂度越高，其值越小，则表明序列更具规律性。本文中，分形维数采用的是盒维数[23]计算方法，经过反复实验，选定网格的最大边长
cellmax=2048 。2.2.3 分类器及评价指标
线性判别分类器(也称Fisher线性判别)的基本实现方法是将特征向量投影到一条直线或一个超平面上(即高维特征映射到低维空间)以寻找一个最佳投影方向来使样本的类内距离最小而类间距离最大，从而实现模式分类。
LDA算法实现步骤为[24]：
(1)定义一个Fisher准则函数：
JF(Ω)=ΩTSbΩΩTSΩΩ (8) 其中，向量
Ω 是投影的方向向量，Sb 和SΩ 是投影前两类别的类间和类内离散度矩阵。这样求投影方向的问题就转化为求该准则函数最大值的问题。(2)采用Lagrange乘子法求解该函数的极值，令函数的分母为常数
C 作为求解的一个约束条件L(Ω,λ)=ΩTSbΩ−λ(ΩTSΩΩ−C) (9) 式中，
λ 为Lagrange乘子。(3)将式(9)对
Ω 求偏导数，得到最佳的投影方向为Ω∗=SΩ−1(mix−mjx) (10) 其中，
mix 和mjx 为两类样本的均值向量。为评价本文所提方法的有效性，引入分类准确率和互信息两个评价指标。其中，分类准确率公式如式(11)
{分类准确率} \!={\frac{{预测正确分类数量}}{{测试总数量}}\times100\% (11) 互信息计算公式如式(12)
MI=0.5log2(SNRt)+1 (12) 其中，
SNRt 表示信噪比，其表达式为SNRt=2var3var1+var2−1 (13) var1 和var2 分别表示左手想象和右手想象的评估值集合的方差，var3 为所有评估值集合的方差。互信息值越大，则表示系统具有良好的分类效果，分类结果越可信。两种评价指标结合的评价标准能够更可信地评估系统分类效果的好坏。为保证实验结果的可靠性，本文严格按照竞赛给出的训练集和测试集将实验数据进行划分，采用4折交叉验证方式进行了50次随机实验，将50次实验所得到的平均识别率作为最终的实验结果。
3. 实验结果
本文所有实验均在Windows64位系统下的MATLAB R2014a实验环境下运行，系统内存8 GB，主频 3.70 GHz。为验证本文所提出算法的有效性，采用第2届和第3届国际脑-机接口竞赛数据集对本文算法进行验证。为了方便起见，用S1, S2, S3, S4分别代表dataset Ⅲ受试者以及dataset Ⅲb受试者O3VR, X11, S4。
以受试者S2为例，分别对小波系数能量，AR系数，分形维数3类特征进行计算。设
Q =2,r =3,J =7, AR阶数为4, C3le和C4le分别表示由C3电极和C4电极采集到的左手运动数据，C3ri和C4ri则表示由C3电极和C4电极采集到的右手运动数据。图2为小波系数能量，AR系数和分形维数的盒图。图2(a)为8个子频带d1, d2, ···, d7, c7的小波系数能量计算结果，图2(b)为4个AR系数
AR(2) ～AR(5) 的计算结果，由于a(1) 数据均为1故忽略其值，图2(c)为2个分形维数的计算结果。实验结果表明，C3le和C4le的数据离散程度、盒子长度以及上下隔间的形状相似度很高，同时，C3ri和C4ri的数据离散程度及偏态也十分相近，且左右手区分度明显。AR系数作为实验所采用的时频特征，为取得最佳分类效果，本文通过4折交叉验证方式最终确定了AR模型阶数：对于受试者S1和S4，其阶数设置为6；对于受试者S2和S3，其阶数设置为4。
为验证所提算法的有效性，本文使用不同特征组合进行了对比实验。其中，F1, F2, F3分别表示小波系数能量、AR系数和分形维数特征，F1+F2代表使用能量和AR系数特征，F1+F3代表使用能量和分形维数特征，F2+F3代表使用AR系数和分形维数特征，F1+F2+F3代表使用全部特征。实验结果如图3所示。
为更直观体现采用组合特征后识别率的变化，表1给出了不同受试者采用单一特征和组合特征得到的平均识别率及最高识别率的对比。结合图表可以看出，尽管由于受试者对于不同实验任务的敏感度不同导致识别误差有所差异，但由于组合特征的加入，4名受试者的识别率表现均取得了一定幅度的提升。
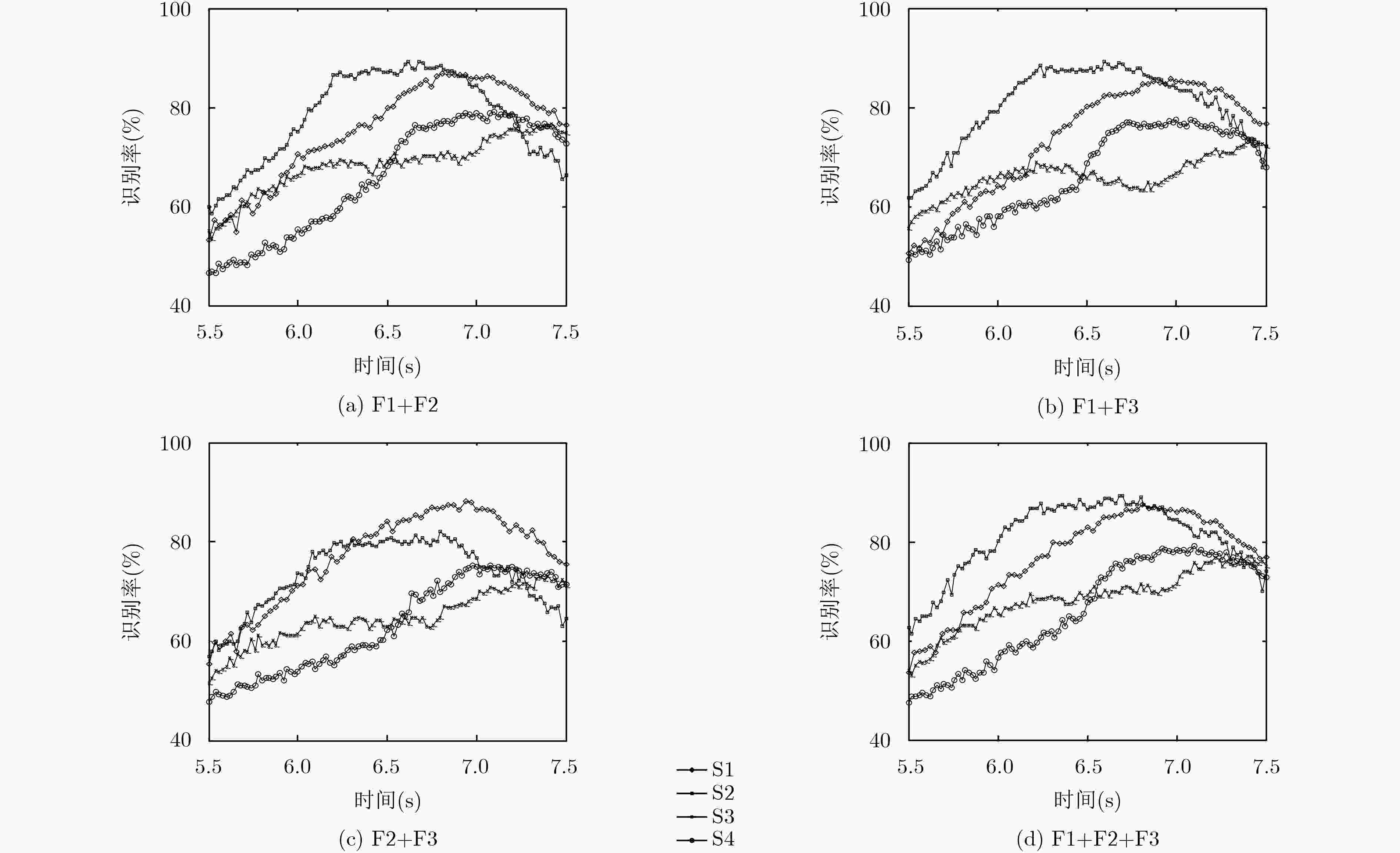
表 1 不同受试者采用单一特征和组合特征所得平均识别率及最高识别率受试者 特征组合 平均识别率(%) 最高识别率(%) F1 81.74 86.44 F2 80.95 85.66 F3 67.93 73.38 S1 F1+F2 86.16 86.90 F1+F3 84.76 85.47 F2+F3 85.03 86.89 F1+F2+F3 86.45 88.11 F1 84.20 89.04 F2 76.52 81.06 F3 55.87 61.20 S2 F1+F2 87.85 89.30 F1+F3 87.63 88.59 F2+F3 80.22 81.33 F1+F2+F3 87.96 89.33 F1 66.08 71.46 F2 66.30 68.93 F3 55.16 58.92 S3 F1+F2 75.61 76.99 F1+F3 71.40 73.08 F2+F3 71.49 72.72 F1+F2+F3 74.70 77.13 F1 73.24 77.87 F2 69.10 74.60 F3 52.36 58.34 S4 F1+F2 77.65 78.79 F1+F3 76.14 77.24 F2+F3 74.06 75.25 F1+F2+F3 76.73 78.80 表2给出了本文方法和近期使用相同数据集的其他方法所取得的最高识别率的对比结果。文献[5]通过幅频分析法提取了相空间特征并对其中的非线性动力学特征进行分析；文献[6]使用基于粒子群优化的环形拓扑方法对分类器进行调优；本文所提方法则是考虑到了信号的时频域以及非线性动力学特性。考虑不同受试者的表现具有差异性，表2也给出了4名受试者识别率的平均值。由表2可知，本文方法的平均值均高于其他两种对比方法。
表3给出了使用本文方法和BCI2003竞赛前3名获胜者以及上述两组对比实验方法的结果比较，分类结果评价指标使用了最大互信息和最小错误识别率[25]。由于识别率这一评价指标仅仅考虑到分类器的输出结果，而忽略了输出量这一概念，其并不完全具备描述分类结果置信度的作用，因此本文同时引入最大互信息这一评价指标来评估分类结果的置信度。实验结果表明，本文提出的方法所取得的互信息值较BCI2003竞赛成绩以及对比实验方法具有显著优势。
4. 讨论
脑电信号是一种非线性信号，传统的时频域特征提取方法忽略了这一特性，丢失了非线性特征的特征提取方法会导致一个较低的系统识别率[26]。本文所提方法对TQWT得到的多个子频带进行处理，兼顾了信号的时频特征和非线性特征，取得了较高的分类精度。由于实验时间的4～8 s正处于受试者思维意识稳定阶段，其表现力为最佳时期，故选取此阶段进行实验验证。实验中利用滑动窗提取信号子频带的特征，通过揭示单位时间段内信号的变化，更细致地描述了两种运动想象状态。
考虑到个体间的差异性，在信号的分解中，需对TQWT3个可调参数进行调整。通过反复实验，得出实现最佳分类效果的S1, S2, S3, S4的
Q ,r ,J 值分别设置如表4所示。表 4 不同受试者TQWT参数设置受试者 Q r J S1 1 3 2 S2 2 3 7 S3 1 3 2 S4 2 3 3 为保证时频特征的选取能够较为全面地描述信号的时频特性，本文同时应用小波系数能量和AR系数两种时频特征，达到了较高的识别率。除时频特征的应用外，本文还引入非线性特征—分形维数。通过图3和表1可以看出，加入分形维数特征后，系统的识别率明显提升。
表2和表3将本文所提方法和文献[5,6]方法以及竞赛方法取得的结果进行了比较，使用识别率和互信息2个指标对分类结果进行了综合评价，取得了83.34%的平均最高识别率以及0.95的最大互信息，体现出了良好的竞争力。
同时，为探讨本文算法的计算复杂度问题，还统计了在当前实验环境下单次特征提取过程的时耗以及4名受试者脑电任务的识别时间，如表5所示。实验中对于单试次数据长度取3 s进行论证，可以看出，本文方法所需的时耗和识别时间是可以基本满足在线BCI系统要求的。
表 5 本文方法的时耗统计(s)TQWT过程 能量特征 AR系数特征 分形维数特征 分类 总时间 S1 0.0010 0.0012 0.0016 0.0559 0.0174 0.0771 S2 0.0022 0.0010 0.0015 0.0536 0.0166 0.0749 S3 0.0012 0.0010 0.0016 0.0533 0.0163 0.0734 S4 0.0014 0.0015 0.0018 0.0547 0.0171 0.0765 5. 结束语
本文采用TQWT方法对脑电信号进行特征提取，对所有子频带计算小波系数能量、AR系数和分形维数作为特征，之后对所提取的特征使用LDA分类器进行分类，实现了对左右手运动想象脑电任务的分类。实验结果表明，本文所提方法可以对左右手运动想象2类任务进行准确分类，最高和最低分类准确率分别为89.33%和77.13%，最大和最小互信息值分别为0.96和0.43。所提算法为基于运动想象的在线BCI系统应用提供了新的思路。
-
表 1 不同受试者采用单一特征和组合特征所得平均识别率及最高识别率
受试者 特征组合 平均识别率(%) 最高识别率(%) F1 81.74 86.44 F2 80.95 85.66 F3 67.93 73.38 S1 F1+F2 86.16 86.90 F1+F3 84.76 85.47 F2+F3 85.03 86.89 F1+F2+F3 86.45 88.11 F1 84.20 89.04 F2 76.52 81.06 F3 55.87 61.20 S2 F1+F2 87.85 89.30 F1+F3 87.63 88.59 F2+F3 80.22 81.33 F1+F2+F3 87.96 89.33 F1 66.08 71.46 F2 66.30 68.93 F3 55.16 58.92 S3 F1+F2 75.61 76.99 F1+F3 71.40 73.08 F2+F3 71.49 72.72 F1+F2+F3 74.70 77.13 F1 73.24 77.87 F2 69.10 74.60 F3 52.36 58.34 S4 F1+F2 77.65 78.79 F1+F3 76.14 77.24 F2+F3 74.06 75.25 F1+F2+F3 76.73 78.80 
下载: 导出CSV
下载: 导出CSV
下载: 导出CSV
表 5 本文方法的时耗统计(s)
TQWT过程 能量特征 AR系数特征 分形维数特征 分类 总时间 S1 0.0010 0.0012 0.0016 0.0559 0.0174 0.0771 S2 0.0022 0.0010 0.0015 0.0536 0.0166 0.0749 S3 0.0012 0.0010 0.0016 0.0533 0.0163 0.0734 S4 0.0014 0.0015 0.0018 0.0547 0.0171 0.0765
下载: 导出CSV
-
佘青山, 陈希豪, 高发荣. 基于感兴趣脑区LASSO-Granger因果关系的脑电特征提取算法[J]. 电子与信息学报, 2016, 38(5): 1266–1270. doi: 10.11999/JEIT150851SHE Qingshan, CHEN Xihao, and GAO Farong. Feature extraction of electroencephalography based on LASSO-Granger causality between brain region of interest[J]. Journal of Electronics &Information Technology, 2016, 38(5): 1266–1270. doi: 10.11999/JEIT150851 BALCONI M and MAZZA G. Brain oscillations and BIS/BAS (behavioral inhibition/activation system) effects on processing masked emotional cues. ERS/ERD and coherence measures of alpha band[J]. International Journal of Psychophysiology, 2009, 74(2): 158–165. doi: 10.1016/j.ijpsycho.2009.08.006 吕俊, 谢胜利, 章晋龙. 脑-机接口中基于ERS/ERD的自适应空间滤波算法[J]. 电子与信息学报, 2009, 31(2): 314–318.LV Jun, XIE Shengli, and ZHANG Jinlong. Adaptive spatial filter based on ERD/ERS for brain-computer interfaces[J]. Journal of Electronics &Information Technology, 2009, 31(2): 314–318. 陈强, 陈勋, 余凤琼. 基于独立向量分析的脑电信号中肌电伪迹的去除方法[J]. 电子与信息学报, 2016, 38(11): 2840–2847. doi: 10.11999/JEIT160209CHEN Qiang, CHEN Xun, and YU Fengqiong. Removal of muscle artifact from EEG data based on independent vector analysis[J]. Journal of Electronics &Information Technology, 2016, 38(11): 2840–2847. doi: 10.11999/JEIT160209 CHEN Minyou, FANG Yonghui, and ZHENG Xufei. Phase space reconstruction for improving the classification of single trial EEG[J]. Biomedical Signal Processing & Control, 2014, 11(1): 10–16. doi: 10.1016/j.bspc.2014.02.002 HAMID M and ZABIHOLLAH S M. Improvement of EEG-based motor imagery classification using ring topology-based particle swarm optimization[J]. Biomedical Signal Processing & Control, 2017, 32: 69–75. doi: 10.1016/j.bspc.2016.10.015 PATTNAIK S, DASH M, and SABUT S K. DWT-based feature extraction and classification for motor imaginary EEG signals[C]. International Conference on Systems in Medicine and Biology, Kharagpur, India, 2016: 186–201. 徐佳琳, 左国坤. 基于互信息与主成分分析的运动想象脑电特征选择算法[J]. 生物医学工程学杂志, 2016, 33(2): 201–207. doi: 10.7507/1001-5515.20160036XU Jialin and ZUO Guokun. Motor imagery electroencephalogram feature selection algorithm based on mutual information and principal component analysis[J]. Journal of Biomedical Engineering, 2016, 33(2): 201–207. doi: 10.7507/1001-5515.20160036 罗志增, 周镇定, 周瑛. 双树复小波特征在运动想象脑电识别中的应用[J]. 传感技术学报, 2014, 27(5): 575–580. doi: 10.3969/j.issn.1004-1699.2014.05.001LUO Zhizeng, ZHOU Zhending, and ZHOU Ying. The application of DTCWT feature in recognition of motor imagery[J]. Journal of Sensors and Actuators, 2014, 27(5): 575–580. doi: 10.3969/j.issn.1004-1699.2014.05.001 周瑛. 虚拟场景下运动想象脑电信号识别研究[D]. [硕士论文], 杭州电子科技大学, 2013.ZHOU Ying. The research of motor imagery recognition in virtual reality[D]. [Master dissertation], Hangzhou Dianzi University, 2013. AL-QAZZAZ N K, HAMID B M A S, AHMAD S A, et al. Automatic artifact removal in EEG of normal and demented individuals using ICA-WT during working memory tasks[J]. Sensors, 2017, 17(6): 1–25. doi: 10.3390/s17061326 GHORBANIAN P, DEVILBISS D M, VERMA A, et al. Identification of resting and active state EEG features of Alzheimer’s disease using discrete wavelet transform[J]. Annals of Biomedical Engineering, 2013, 41(6): 1243–1257. doi: 10.1007/s10439-013-0795-5 HASSAN A R and BHUIYAN M I H. An automated method for sleep staging from EEG signals using normal inverse Gaussian parameters and adaptive boosting[J]. Neurocomputing, 2017, 219: 76–87. doi: 10.1016/j.neucom.2016.09.011 BENJAMIN B. BCI Competition II[OL]. http://www.bbci.de/competition/ii/, 2003. BENJAMIN B. BCI Competition III[OL]. http://www.bbci.de/competition/iii/, 2005. VIDAURRE C, SCHLOGL A, CABEZA R, et al. A fully on-line adaptive BCI[J]. IEEE Transactions on Biomedical Engineering, 2006, 53(6): 1214–1219. doi: 10.1109/TBME.2006.873542 BAYRAM I and SELESNICK I W. Frequency-domain design of overcomplete rational-dilation wavelet transforms[J]. IEEE Transactions on Signal Processing, 2009, 57(8): 2957–2972. doi: 10.1109/TSP.2009.2020756 IVAN S. Tunable Q-factor wavelet transform[OL]. http://eeweb.poly.edu/iselesni/TQWT/index.html, 2016. SELESNICK I W. Wavelet transform with tunable Q-factor[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3560–3575. doi: 10.1109/TSP.2011.2143711 AMIN H U, MALIK A S, AHMAD R F, et al. Feature extraction and classification for EEG signals using wavelet transform and machine learning techniques[J]. Australasian Physical & Engineering Sciences in Medicine, 2015, 38(1): 139–149. doi: 10.1007/s13246-015-0333-x LAWHERN V, HAIRSTON W D, MCDOWELL K, et al. Detection and classification of subject-generated artifacts in EEG signals using autoregressive models[J]. Journal of Neuroscience Methods, 2012, 208(2): 181–189. doi: 10.1016/j.jneumeth.2012.05.017 PHOTHISONOTHAI M and NAKAGAWA M. EEG-based classification of motor imagery tasks using fractal dimension and neural network for brain-computer interface[J]. IEICE Transactions on Information and Systems, 2008, 91(1): 44–53. doi: 10.1093/ietisy/e91-d.1.44 訾艳阳, 胥永刚, 何正嘉. 离散振动信号分形盒维数的改进算法和应用[J]. 机械科学与技术, 2001(3): 373–376. doi: 10.3321/j.issn:1003-8728.2001.03.021ZI Yanyang, XU Yonggang, and HE Zhengjia. Fractal box dimension of discrete vibration signals[J]. Mechanical Science and Technology for Aerospace Engineering, 2001(3): 373–376. doi: 10.3321/j.issn:1003-8728.2001.03.021 GUPTA S and SAINI H. EEG features extraction using PCA plus LDA approach based on L1-norm for motor imaginary classification[C]. IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 2015: 1–5. SCHLOGL A, KEINRATH C, SCHERER R, et al. Information transfer of an EEG-based brain computer interface[C]. International IEEE EMBS Conference on Neural Engineering, Capri Island, Italy, 2003: 641–644. FELE-ZORZ G, KAVSEK G, NOVAK-ANTOLIC Z, et al. A comparison of various linear and non-linear signal processing techniques to separate uterine EMG records of term and pre-term delivery groups[J]. Medical & Biological Engineering & Computing, 2008, 46(9): 911–922. doi: 10.1007/s11517-008-0350-y 期刊类型引用(6)
1. 汤伟，耿逸飞. 基于DTCWT的运动想象脑电特征提取. 计算机应用与软件. 2023(04): 80-84+106 . 
百度学术2. 刘朕，朱炳宇，张景祥. EEG信号识别中可调优化Q因子小波变换的多特征融合算法. 控制理论与应用. 2022(12): 2302-2312 . 百度学术3. 张小内，翟文鹏，侯惠让，孟庆浩. 基于ReliefF-Pearson的嗅觉脑电通道选择. 电子与信息学报. 2021(07): 2032-2037 . 
本站查看4. 王璐慧，王越，钱梦瑶，董亚非. 基于氧化石墨烯与金属离子的逻辑模型设计与可控性验证. 电子与信息学报. 2020(06): 1410-1419 . 本站查看5. 张睿琳，贾建，张瑞. 基于TWQT和熵特征的癫痫脑电快速检测. 西北大学学报(自然科学版). 2020(04): 571-581 . 百度学术6. 罗婷瑞，贾建，张瑞. 基于可调Q因子小波变换和迁移学习的癫痫脑电信号检测. 计算机科学. 2020(07): 199-205 . 百度学术其他类型引用(16)
-
下载:
百度学术
计量
- 文章访问数: 2601
- HTML全文浏览量: 805
- PDF下载量: 82
- 被引次数: 22
下载:
