BeiDou Navigation Satellite System in Challenge Environment Using an Atomic Clock and Barometric Altimeter
-
摘要: 在城市峡谷等遮挡环境下,接收机无法连续进行定位解算;并且高程定位精度不能满足用户在立交桥或者盘山公路等环境下的定位需求。在接收机内使用原子钟,可以利用原子钟的高稳定性,对钟差进行高精度的预测。并通过与气压测高仪共同辅助北斗系统定位,可以有效提高接收机的定位精度和连续性;该文首先理论分析了原子钟和气压测高仪辅助定位算法;然后,提出一种气压测高仪初始化校正方法,并通过对钟差噪声类型的分析确定了钟差预测方法;最后,模拟遮挡环境,进行原子钟和气压测高仪辅助北斗卫星导航系统定位试验,并分析了定位结果。结果表明:仅跟踪两颗可见卫星,便可以进行定位解算,并且垂直方向上的定位误差从8.2 m (RMSE)下降到了5.2 m,定位结果的波动从4.6 m下降到了0.8 m。Abstract: The vertical positioning accuracy of BeiDou satellite navigation System (BDS) and the continuity of receiver in the challenge environment can not satisfy the user demand. If atomic clocks are used in the receiver, the high stability of the atomic clock can be used for long time and high precision prediction of receiver clock bias. The positioning accuracy and continuity are improved by using atomic clock and barometric altimeter. This article first analyzes the atomic clocks and barometric altimeter aided BDS positioning algorithm; Then, correction method is proposed for initialization of barometric altimeter, and analysis on the difference of noise type clock is used to determine the clock bias prediction method; Finally, positioning experiment of the atomic clock and barometric altimeter aided BDS in simulation challenge environment is carried out, and the positioning result is analyzed. The results show that BDS can positioning solution to track two visible satellites, and vertical positioning accuracy is significantly improved. The positioning error in the vertical direction is decreased from 8.2 m (RMSE) to 5.2 m, and the fluctuation of the positioning results decreased from 4.6 m to 0.8 m.
-
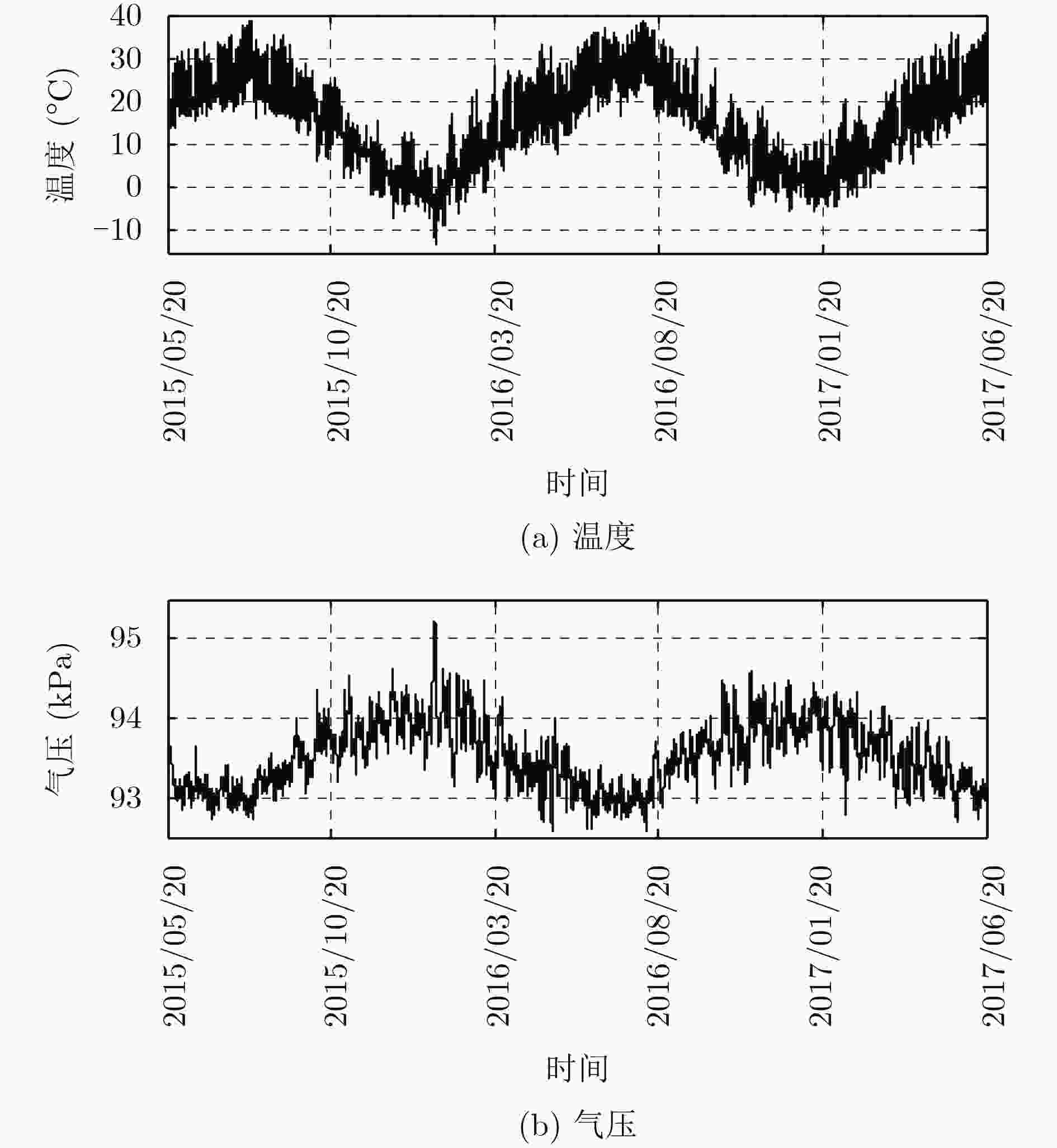
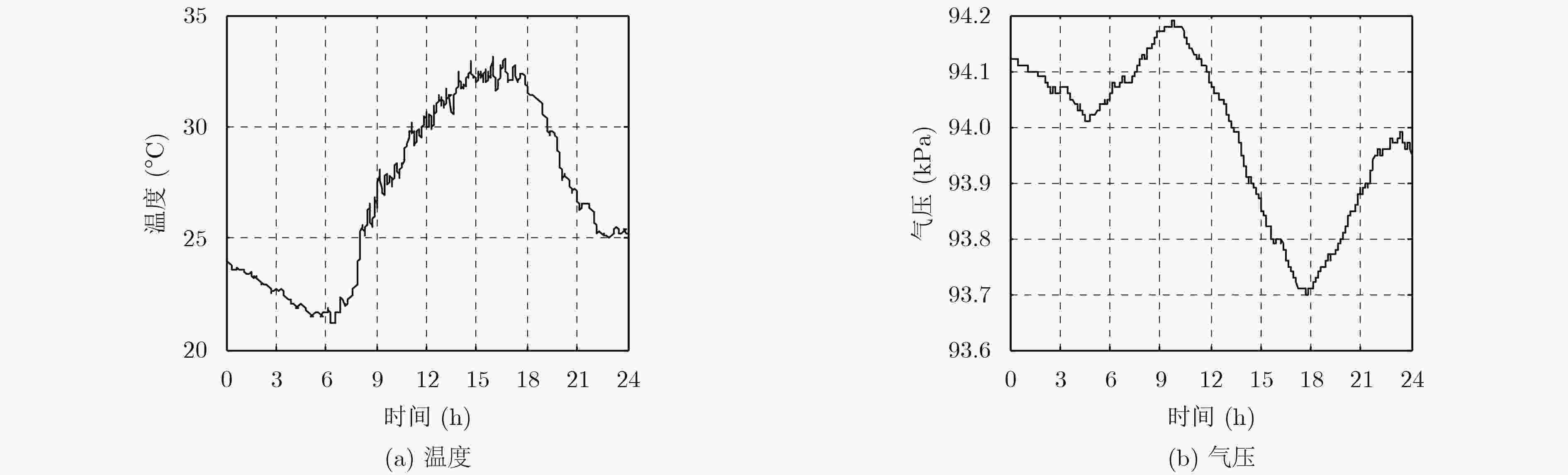
表 1 不同时长内气压、温度最大变化量的均方根误差
时间(min) 气压(kPa) 温度(°C) 15 0.017 0.44 30 0.030 0.69 45 0.043 0.92 60 0.055 1.12 表 2 在不同温度和不同气压条件下,气压每变化0.01 kPa对高度的影响(m)
气 压 (kPa) 温度(°C) –40 –20 0 20 40 100 0.68 0.74 0.80 0.86 0.92 90 0.76 0.82 0.89 0.95 1.02 80 0.85 0.93 1.00 1.07 1.15 60 1.14 1.24 1.33 1.43 1.53 表 3 不同时长内,气压测高仪测量高度的误差(RMS)
时长(min) 15 30 45 60 高度(m) 1.54 2.73 3.97 4.97 表 4 1 个小时内各个方向上的定位误差
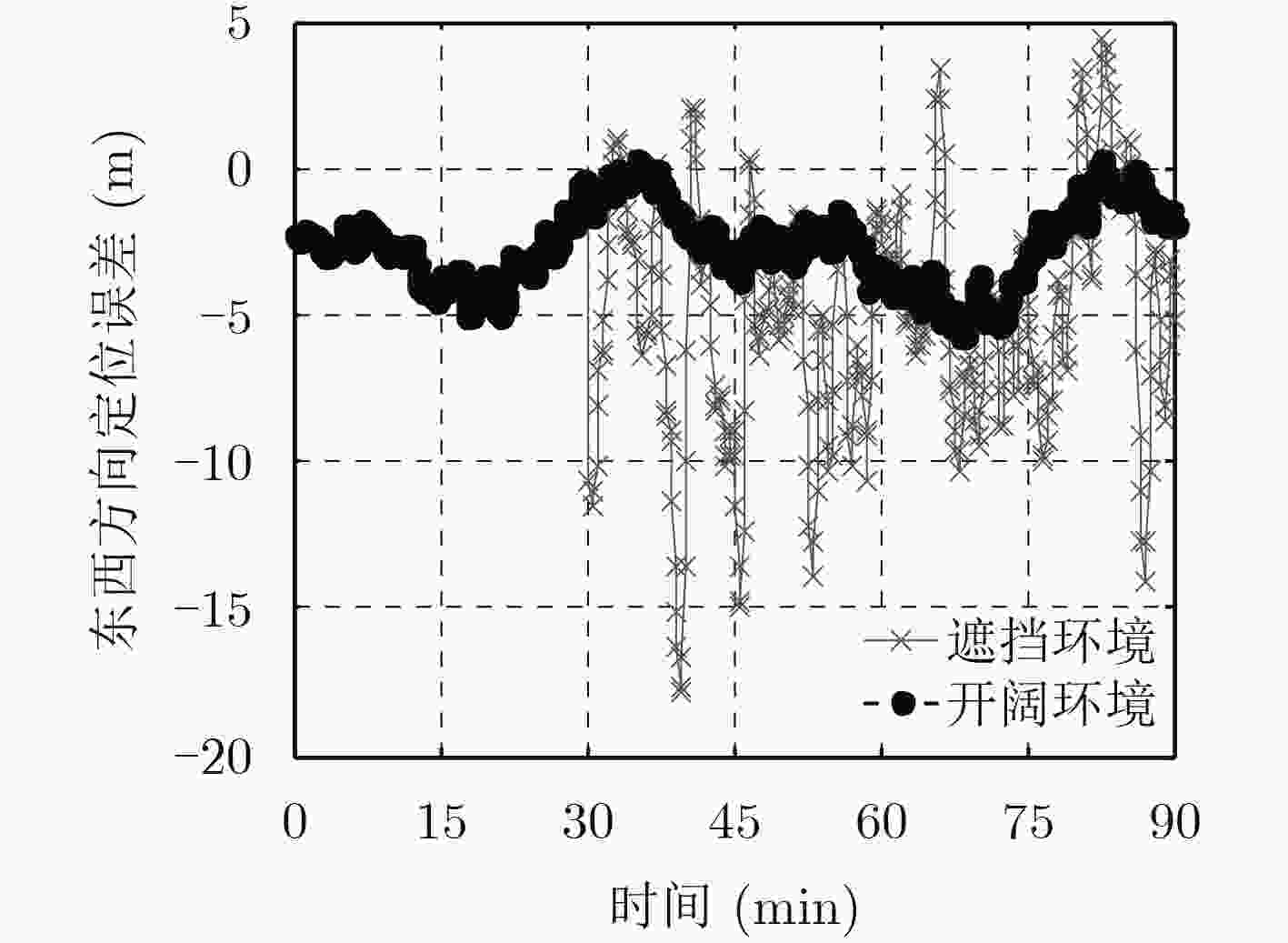
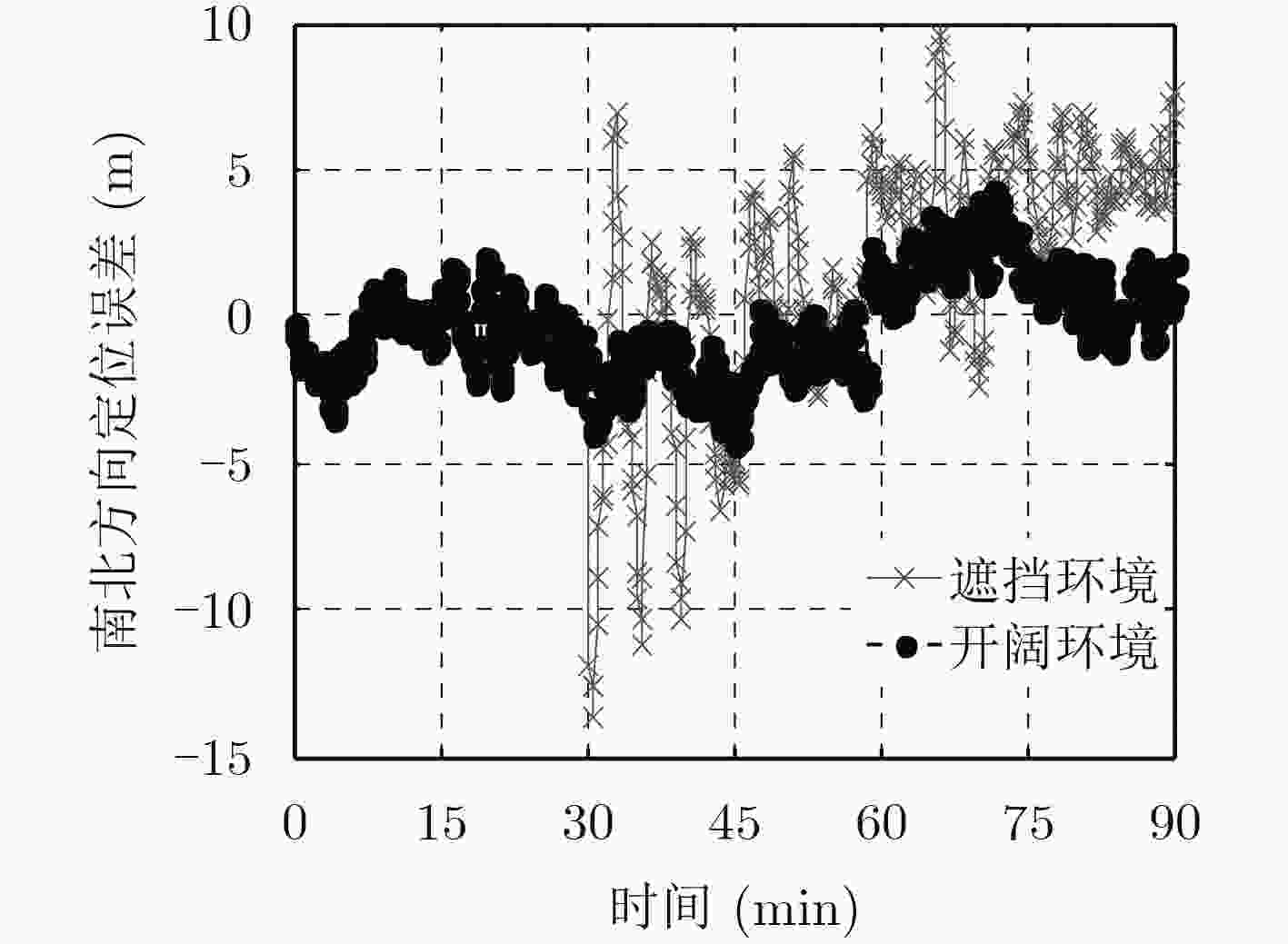
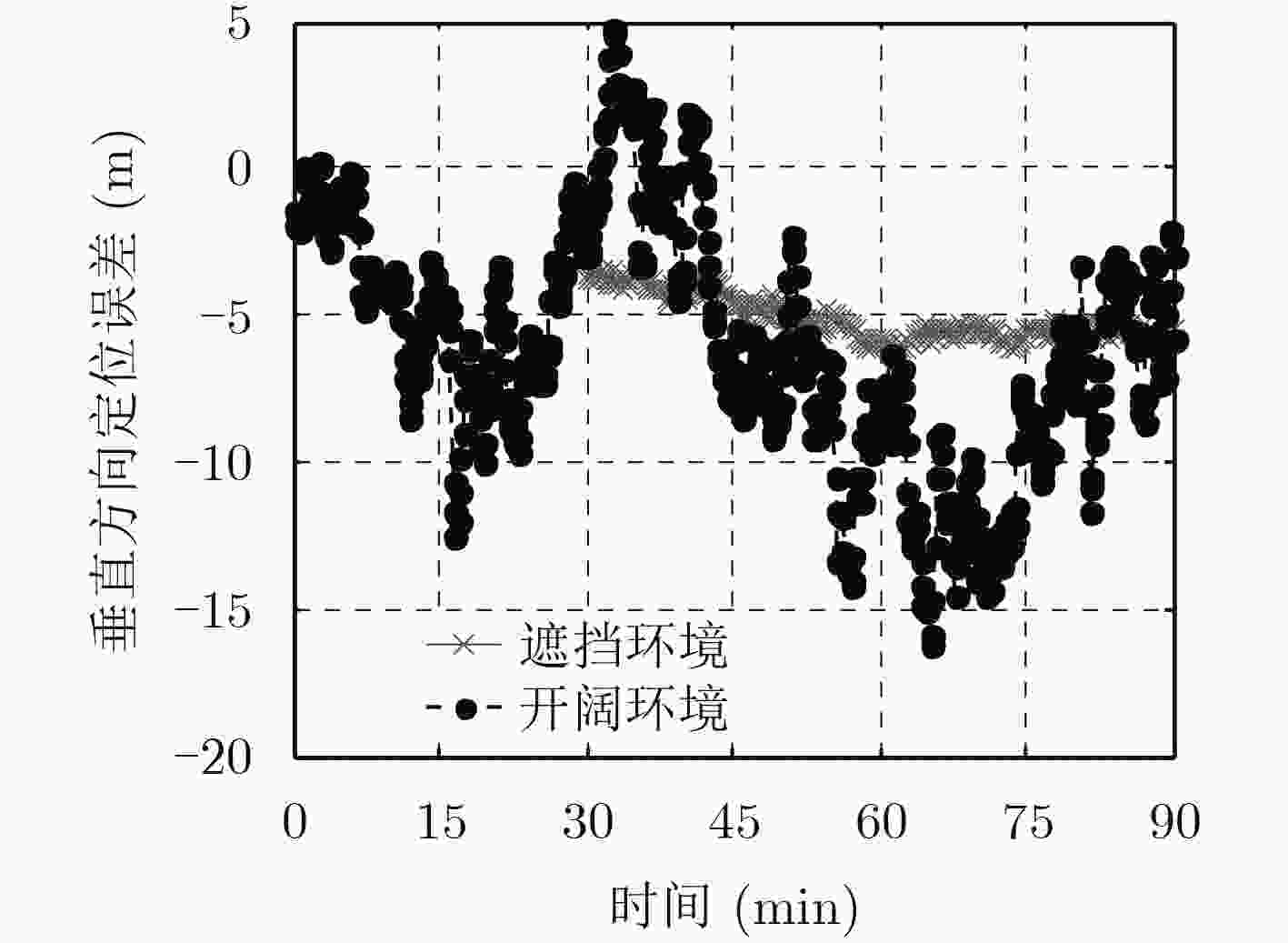
RMSE (m) Std (m) 开阔环境 遮挡环境 开阔环境 遮挡环境 东西方向 2.9 6.6 1.5 4.1 南北方向 1.9 4.5 1.9 4.3 垂直方向 8.2 5.2 4.6 0.8 -
ZHANG Jieying, EZZALDEEN E, ZHOU Junchuan, et al. Performance investigation of barometer aided GPS/MEMS-IMU integration[C]. Position Location and Navigation Symposium (PLANS), Myrtle Beach, 2012: 598–604. KUBO N, TOKURA H, and PULLEN S. Mixed GPS-BeiDou RTK with inter-systems bias estimation aided by CSAC[J]. GPS Solutions, 2018, 22(1): 5 doi: 10.1007/s10291-017-0670-1 CALERO D and FERNANDEZ E. Characterization of chip-scale atomic clock for GNSS navigation solutions[C]. International Association of Institutes Navigation World Congress(IAIN), Prague, 2015: 1–8. RAMLALL R, STREETER J, and SCHBECKER J F. Three satellite navigation in an urban canyon using a chip-scale atomic clock[C]. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, 2011: 2937–2945. ZHOU Weili, HUANG Chao, SONG Shuli, et al. Characteristic analysis and short-term prediction of GPS/BDS satellite clock correction[C]. China Satellite Navigation Conference (CSNC) 2016 Proceedings, Changsha, 2016, 3: 187–200. MISRA P N. Clock-aided satellite navigation receiver system for enhanced position estimation and integrity monitoring[P]. USA Patent, 1997, US5623414A. LIU Chang, XU Feng, QU Yongsheng, et al. Analysis on factors influencing frequency drift of rubidium clocks for satellite navigation[C]. China Satellite Navigation Conference (CSNC) 2016 Proceedings, Changsha, 2016, 3: 645–652. KRAWINKEL T and SCHON S. Benefits of receiver clock modeling in code-based GNSS navigation[J]. GPS Solutions, 2015, 20(4): 1–15 doi: 10.1007/s10291-015-0480-2 孙健. GPS和高精度气压高度表的组合导航定位技术研究[D]. [硕士论文], 南京航空航天大学, 2008.SUN Jian. Research on GPS and high precision baro-altimeter integrated navigation and positioning technology[D]. [Master dissertation], Nanjing University of Aeronautics and Astronautics, 2008. 李博, 李孝辉. 气压测高仪的设计与实现[J]. 国外电子测量技术, 2017, 36(1): 53–56 doi: 10.3969/j.issn.1002-8978.2017.01.014LI Bo and LI Xiaohui. Design and implementation of barometric altimeter[J]. Foreign Electronic Measurement Technology, 2017, 36(1): 53–56 doi: 10.3969/j.issn.1002-8978.2017.01.014 KAPLAN E D and HEGARTY C. Understanding GPS: Principles and Applications[M]. London: Artech House, 2005: 336. KLINE P A. Atomic clock augmentation for receivers using the Global Positioning System[D]. [Ph.D. dissertation], Virginia Polytechnic Institute and State University, 1997: 55–57. ALLAN D W. Should the classical variance be used as a basic measure in standards metrology?[J]. IEEE Transactions on Instrumentation and Measurement, 1987, IM-36(2): 646–654 doi: 10.1109/TIM.1987.6312761 李孝辉. 时间频率信号的精密测量[M]. 北京: 科学出版社, 2010: 34.LI Xiaohui. Precise Measurement of Time and Frequency Signals[M]. Beijing: Science Press, 2010: 34. RILEY W J. Handbook of frequency stability analysis[J]. NIST, 2007, 1065: 1–123. ALLAN D W. Time and frequency (time-domain) characterization, estimation, and prediction of precision clocks and oscillators[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 1987, 34(6): 647–654 doi: 10.1109/T-UFFC.1987.26997 -





 下载:
下载:


 下载:
下载:
