Study on Multi-target Angle Tracking Algorithm of Bistatic MIMO Radar with Unknown Target Number
-
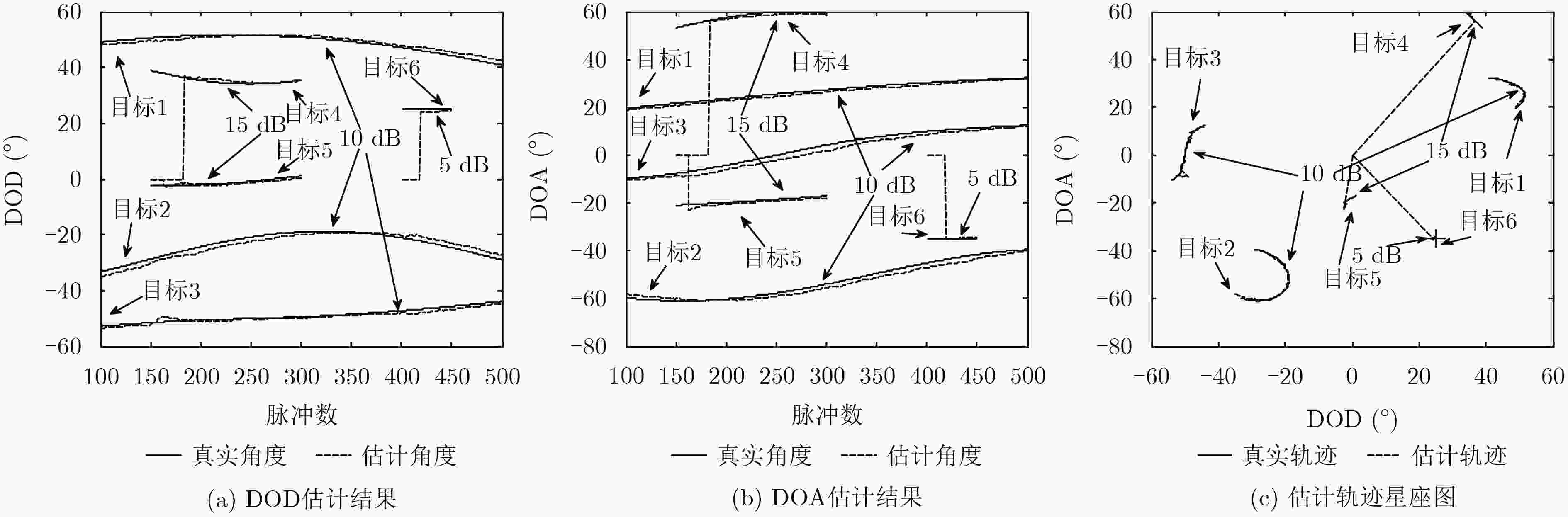
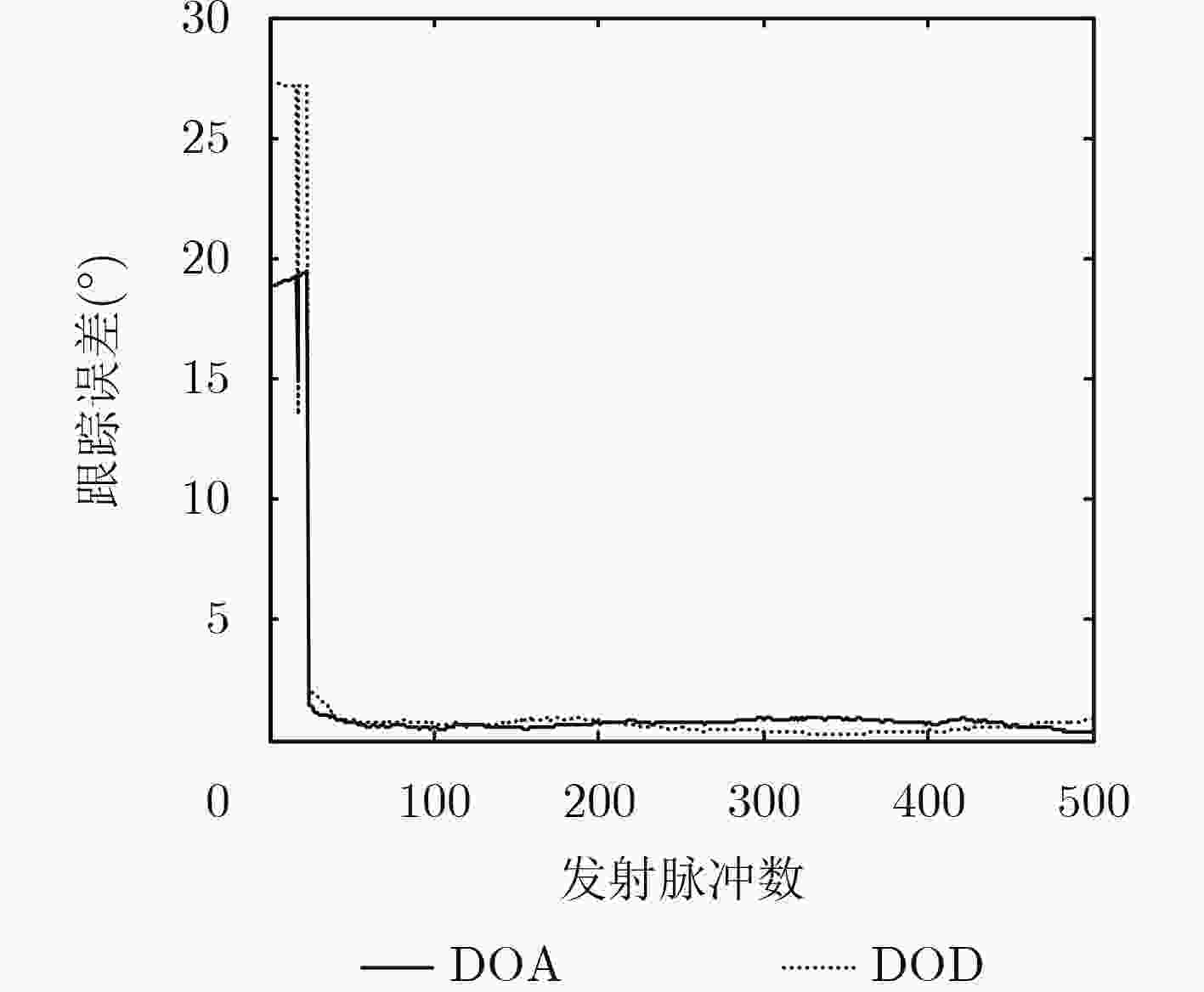
摘要: 针对目标个数未知时双基地MIMO雷达角度跟踪问题,该文提出一种基于改进自适应非对称联合对角化(AAJD)的目标个数与角度联合跟踪算法。AAJD算法中无法得到特征值变量,因此改进AAJD算法引入主成分顺序估计思想,循环求出特征值,然后运用改进信息论准则估计出目标个数。其次提出目标个数防抖动算法,提高了稳健性。最后改进了ESPRIT算法,完成了目标参数的自动配对和关联。仿真结果表明改进AAJD算法能够成功跟踪目标个数和角度,验证了理论分析的有效性。Abstract: In order to solve the angle tracking problem of bistatic MIMO radar when the number of target is unknown, a joint tracking algorithm of the number of target and the angle is proposed. There is no variable in Adaptive Asymmetric Joint Diagonalization (AAJD) algorithm that can directly represent the eigenvalue. Therefore, the idea of principal component sequence estimation is introduced to the improved AAJD algorithm, and the eigenvalues are iteratively evaluated. Then, the number of target is estimated by using the improved information theory. Secondly, the anti-dithering algorithm of target number is proposed, which improves the robustness of the algorithm. Finally, the ESPRIT algorithm is improved to realize the automatic matching and association of DOD and DOA. The simulation results show that the improved AAJD algorithm can successfully track the number of target and angle trajectories. The efficiency of the proposed method is verified.
-
表 1 改进AAJD算法流程
初始值: ${{P}}\left( 0 \right) = {{{I}}_{P \times P}}$, $0 < \beta \le 1$, $K$为稳定脉冲数 输入: ${{y}}\left( t \right)$ 输出: $φ \left( t \right),{θ} \left( t \right)$ For $t = 1,2, ·\!·\!· ,T\,$ 步骤 1 for $i = 1,2, ·\!·\!· ,L$ ${d_i}\left( t \right) = {{W}}\!_i\,^{ - 1}\left( {t - 1} \right){{{y}}_i}\left( t \right)$ ${g_i}\left( t \right)\; = \beta {g_i}\left( {t - 1} \right) + {\left| {{d_i}\left( t \right)} \right|^2}$ ${Q_i}\left( t \right) = {{d_i^{*} \left( t \right)} / {{g_i}\left( t \right)}}$ ${\eta _i}\left( t \right) = {{{{\left| {{d_i}\left( t \right)} \right|}^2}} \bigl/ {{g_i}\left( t \right)}}$ ${{{e}}_i}\left( t \right) = {{{y}}_i}\left( t \right) - {{{W}}_i}\left( {t - 1} \right){d_i}\left( t \right)$ ${\widehat{{W}}_i}\left( t \right) = {{{W}}_i}\left( {t - 1} \right) + {1 / {\left( {\beta + {\eta _i}\left( t \right)} \right)}}{{{e}}_i}\left( t \right)Q_i^{}\left( t \right)$ ${{{y}}_{i + 1}}\left( t \right) = {{{y}}_i}\left( t \right) - {\widehat{{W}}}_i^{ - 1}\left( t \right){d_i}\left( t \right)$ end if $t < K$ 对 ${{g}}\!\left( t \right)$进行降序排列,并取最大的 $P$个特征值对应的矢量 构成 ${{W}}\left( t \right)$ else
取前 $P$个特征矢量构成 ${{W}}\!\left( t \right)$end 步骤 2 if $t = = 1$ ${{{Ψ}}_r} = {{W}}\!_{r1}\,\!\!\!^{- 1}{{{W}}\!_{r2}}$, 对 ${{{Ψ}}_r}$进行特征值分解:
${{{Ψ}}_r} = {{T}}{{{Φ}}_r}{{T}}_{}^{ - 1}$,取 ${{{Φ}}_r}$的对角线元素组成 ${{{ω }}_r}$${{{Φ}}_t} = {{{T}}^{ - 1}}{{W}}\!_{t1}\,\!\!\!^{ - 1}{{{W}}\!_{t2}}{{T}}$,取 ${{{Φ}}_t}$的对角线元素组成 ${{{ω }}_t}$ else ${{{Ψ}}_r} = {{W}}\!_{r1}\,\!\!\!^{ - 1}{{{W}}\!_{r2}}$, ${{{Ψ }}_t} = {{W}}\!_{t1}\,^{ - 1}{{{W}}\!_{t2}}$,取 ${{{Ψ}}_r}$和 ${{{Ψ }}_t}$的对角线元 素组成 ${{{ω }}_r}$和 ${{{ω }}_t}$ end 利用 ${\theta _p} = \arcsin \left\{ {{\rm{angle}}\left[ {{{ω}_r}\left( p \right)} \right]/{π} } \right\},$
${\varphi _p} = \arcsin \left\{ {{\rm angle}\left[ {{ω}_r \left( p \right)} \right]/{π} } \right\}$,得到了 ${θ} \left( t \right),φ \left( t \right)$根据 ${{W}}\!\!\left( t \right) \!=\! \left[ {{{{a}}_r}\left( {{\theta _1}} \right) \otimes {{{a}}_t}\left( {{\varphi _1}} \right), ·\!·\!·, {{{a}}_r}\left( {{\theta _P}} \right) \otimes {{{a}}_t}\left( {{\varphi _P}} \right)} \right]$更新 $\widehat{{W}}\!\left( t \right)$ End 表 2 目标个数跟踪过程
输入: ${{y}}\left( t \right)$, ${{W}}\left( t \right)$, $P\left( {t - 1} \right)$,稳定脉冲数 $K$ 输出: $P\left( t \right)$ For $i = 1,2, ·\!·\!· ,L$ ${d_i}\left( t \right) = {{W}}_i^{ - 1}\left( t \right){{{y}}_i}\left( t \right)$ ${g_i}\left( t \right)\; = \beta {g_i}\left( {t - 1} \right) + {\left| {{d_i}\left( t \right)} \right|^2}$ ${{{y}}_{i + 1}}\left( t \right) = {{{y}}_i}\left( t \right) - {\widehat{{W}}}_i^{ - 1}\left( t \right){d_i}\left( t \right)$ End If $t < K$, $K$为稳定脉冲数 ${{g}}\!\left( t \right) = {\left[ {{g_1}\!\left( t \right),{g_2}\left( t \right), ·\!·\!· {g_L}\!\left( t \right)} \right]^{\rm{T}}}$ Else 取 ${{g}}\left( t \right) = \left[ {g_1}\!\left( t \right),{g_2}\!\left( t \right), ·\!·\!· ,{g_{P\left( {t - 1} \right)}}\left( t \right),{g_{P\left( {t - 1} \right) + 1}}\left( t \right),\right. $
$\left.{g_N}\left( {t - 1} \right), ·\!·\!· ,{g_N}\left( {t - 1} \right) \right]^{\rm{T}}$End 根据AIC准则估计出 $t$时刻的目标个数 $P\left( t \right)$,注意当 $t > K$只需求 出前 $P\left( {t - 1} \right) + 1$个AIC值,即可得到全局最小值。 -
FISHER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radar-models and detection performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823–838 doi: 10.1109/TSP.2005.862913 徐旭宇, 李小波, 梁浩, 等. 基于二次虚拟孔径扩展的双基地MIMO雷达相干分布式目标中心角度估计[J]. 电子与信息学报, 2014, 36(4): 953–959 doi: 10.3724/SP.J.1146.2013.00955XU Xuyu, LI Xiaobo, LIANG Hao, et al. Central angle estimation of coherently distributed sources for bistatic MIMO radar on second virtual array aperture extension[J]. Journal of Electronics&Information Technology, 2014, 36(4): 953–959 doi: 10.3724/SP.J.1146.2013.00955 樊劲宇, 顾红, 苏卫民, 等. 基于张量分解的互质阵MIMO雷达目标参数估计[J]. 电子与信息学报, 2015, 37(4): 933–938 doi: 10.11999/JEIT140826FAN Jinyu, GU Hong, SU Weimin, et al. Co-prime MIMO radar multi-parameter estimation based on tensor decomposition[J]. Journal of Electronics&Information Technology, 2015, 37(4): 933–938 doi: 10.11999/JEIT140826 TANG Bo, TANG Jun, and PENG Yingning. MIMO radar waveform design in colored noise based on information theory[J]. IEEE Transactions on Signal Processing, 2010, 58(9): 4684–4697 doi: 10.1109/TSP.2010.2050885 梁浩, 崔琛, 余剑. 基于ESPRIT算法的十字型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1): 80–89 doi: 10.11999/JEIT150402LIANG Hao, CUI Chen, and YU Jian. Reduced-dimensional DOA estimation based on ESPRIT algorithm in monostatic MIMO radar with cross array[J]. Journal of Electronics&Information Technology, 2016, 38(1): 80–89 doi: 10.11999/JEIT150402 TANG Bo and TANG Jun. Joint design of transmit waveforms and receive filters for MIMO radar space time adaptive processing[J]. IEEE Transactions on Signal Processing, 2016, 64(18): 4707–4722 doi: 10.1109/TSP.2016.2569431 刘晓莉, 廖桂生. 基于MUSIC和ESPRIT的双基地MIMO雷达角度估计算法[J]. 电子与信息学报, 2010, 32(9): 2179–2183 doi: 10.3724/SP.J.1146.2009.01459LIU Xiaoli and LIAO Guisheng. Combined MUSIC with ESPRIT algorithm for angle estimation in bistatic MIMO radar system[J]. Journal of Electronics&Information Technology, 2010, 32(9): 2179–2183 doi: 10.3724/SP.J.1146.2009.01459 ZHENG Zhidong and ZHANG Jianyun. Fast method for multi-target localization in bistatic MIMO radar[J]. IEEE Electronics Letters, 2011, 47(2): 138–139 doi: 10.1049/el.2010.2577 梁浩, 崔琛, 余剑. 十字型阵列MIMO雷达高精度二维DOA估计[J]. 雷达学报, 2016, 5(3): 254–264 doi: 10.12000/JR16016LIANG Hao, CUI Chen, and YU Jian. Two-dimensional DOA estimation with high accuracy for MIMO radar using cross array[J]. Journal of Radar, 2016, 5(3): 254–264 doi: 10.12000/JR16016 WU Hailang, ZHANG Xiaofei, FENG Gaopeng, et al. DOA tracking in monostatic MIMO radar using PARAFAC-RLST algorithm[C]. The 3rd International Conference on Information Science and Engineering (ICISE’2011), Yangzhou, China, 2011: 958–961. ZHANG Xiaofei, LI Jianfeng, FENG Gaopeng, et al. Kalman-PASTd based DOA tracking algorithm for monostatic MIMO radar[C]. International Conference on Information, Services and Management Engineering, Beijing, 2011: 220–224. YU Huaxin, ZHANG Xiaofei, CHEN Xueqiang, et al. Computationally efficient DOA tracking algorithm in monostatic MIMO radar with automatic association[J]. International Journal of Antennas and Propagation, 2014(12): 1–10 doi: 10.1155/2014/501478 李丽, 邱天爽. 双基地MIMO雷达目标参数估计及动态跟踪新算法[J]. 信号处理, 2014, 30(2): 155–162LI Li and QIU Tianshang. A novel algorithm for target parameter estimation and dynamic tracking in bistatic MIMO radar system[J]. Journal of Signal Processing, 2014, 30(2): 155–162 张正言, 李小波, 徐旭宇, 等. 双基地MIMO雷达角度快速跟踪算法[J]. 信号处理, 2016, 32(6): 701–706 doi: 10.16798/j.issn.1003-0530.2016.06.009ZHANG Zhengyan, LI Xiaobo, XU Xuyu, et al. Target angle rapid algorithm for bistatic MIMO radar[J]. Journal of Signal Processing, 2016, 32(6): 701–706 doi: 10.16798/j.issn.1003-0530.2016.06.009 WU Hailang and ZHANG Xiaofei. DOD and DOA tracking for bistatic MIMO radar using PASTd without additional angles pairing[C]. IEEE Fifth International Conference on Advanced Computational Intelligence, Nanjing, 2012: 1132–1136. doi: 10.1109/ICACI.2012.6463350. ZHANG Weitao, LOU Shuntian, LI Xiaojun, et al. Tracking multiple target in MIMO radar Via adaptive asymmetric joint diagonalization[J]. IEEE Transactions on Signal Processing, 2016, 64(11): 2880–2893 doi: 10.1109/TSP.2016.2535249 YANG J and KAVEH M. Adaptive eigensubspace algorithms for direction or frequency estimation and tracking[J]. IEEE Transaction on Acoustics, Speech, and Signal Processing, 1988, 36(2): 241–251 doi: 10.1109/29.1516 BANNOUR S and AZIMI-SADJADI M R. An adaptive approach for optimal data reduction using recursive least squares learning method[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, 1992: 297–300. doi: 10.1109/ICASSP.1992.226061. -





 下载:
下载:


 下载:
下载:
