一种基于接入与回传一体化小基站的用户满意度最大化算法

唐伦; 刘云龙; 赵旭; 马润琳; 陈前斌

doi:10.11999/JEIT171169

一种基于接入与回传一体化小基站的用户满意度最大化算法

doi: 10.11999/JEIT171169

重庆邮电大学移动通信技术重点实验室重庆 400065

基金项目: 国家自然科学基金(61571073)

详细信息

作者简介:
唐伦：男，1973 年生，教授，博士，主要研究方向为新一代无线通信网络、异构蜂窝网络、软件定义无线网络等

刘云龙：男，1992 年生，硕士生，研究方向为5G无线自回传网络中的资源分配问题

赵旭：男，1989 年生，硕士生，研究方向为5G移动性管理

马润琳：女，1993 年生，硕士生，研究方向为5G网络切片

陈前斌：男，1967 年生，教授，博士生导师，主要研究方向为个人通信、多媒体信息处理与传输、下一代移动通信网络等

通讯作者:
陈前斌 cqb@cqupt.edu.cn

中图分类号: TN929.5
计量
- 文章访问数: 3107
- HTML全文浏览量: 618
- PDF下载量: 43
- 被引次数: 28
出版历程
- 收稿日期: 2017-12-12
- 修回日期: 2018-05-07
- 网络出版日期: 2018-07-12
- 刊出日期: 2018-09-01

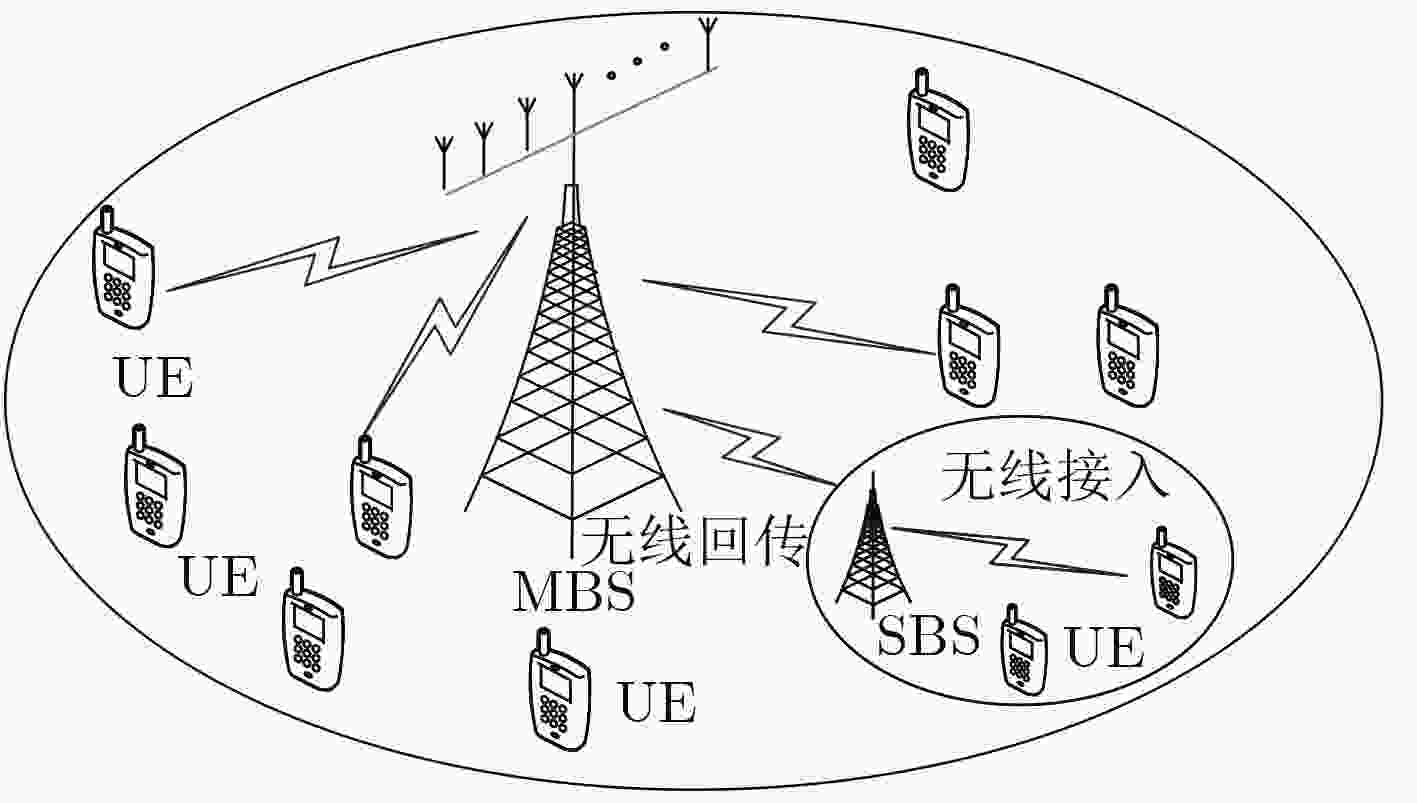
A User Satisfaction Maximization Algorithm Based on Access and Backhaul Integrated Small Base Station

Key Laboratory of Mobile Communication Technology, Chongqing University of Post and Telecommunications, Chongqing 400065, China

Funds: The National Natural Science Foundation of China (61571073)

摘要

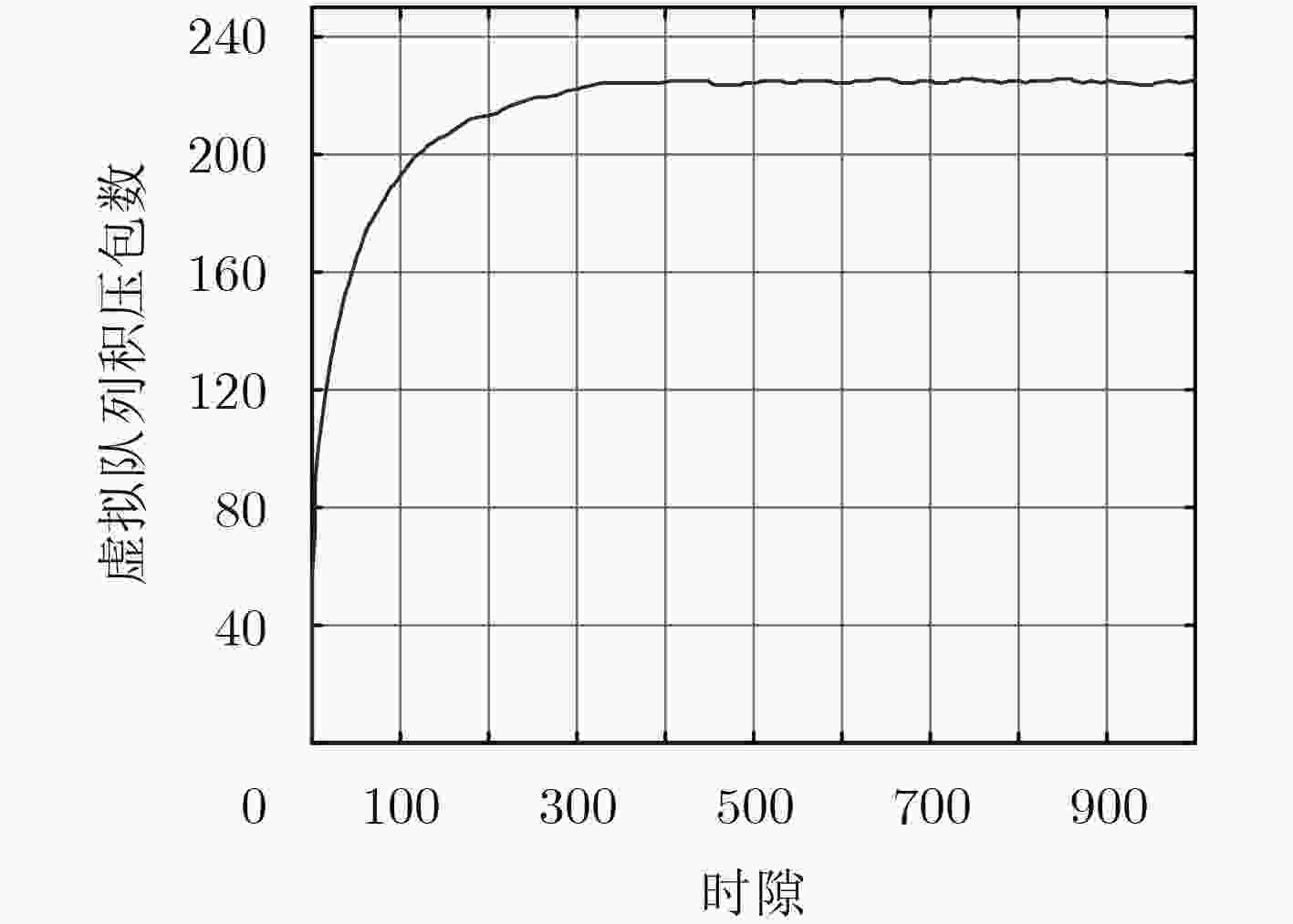
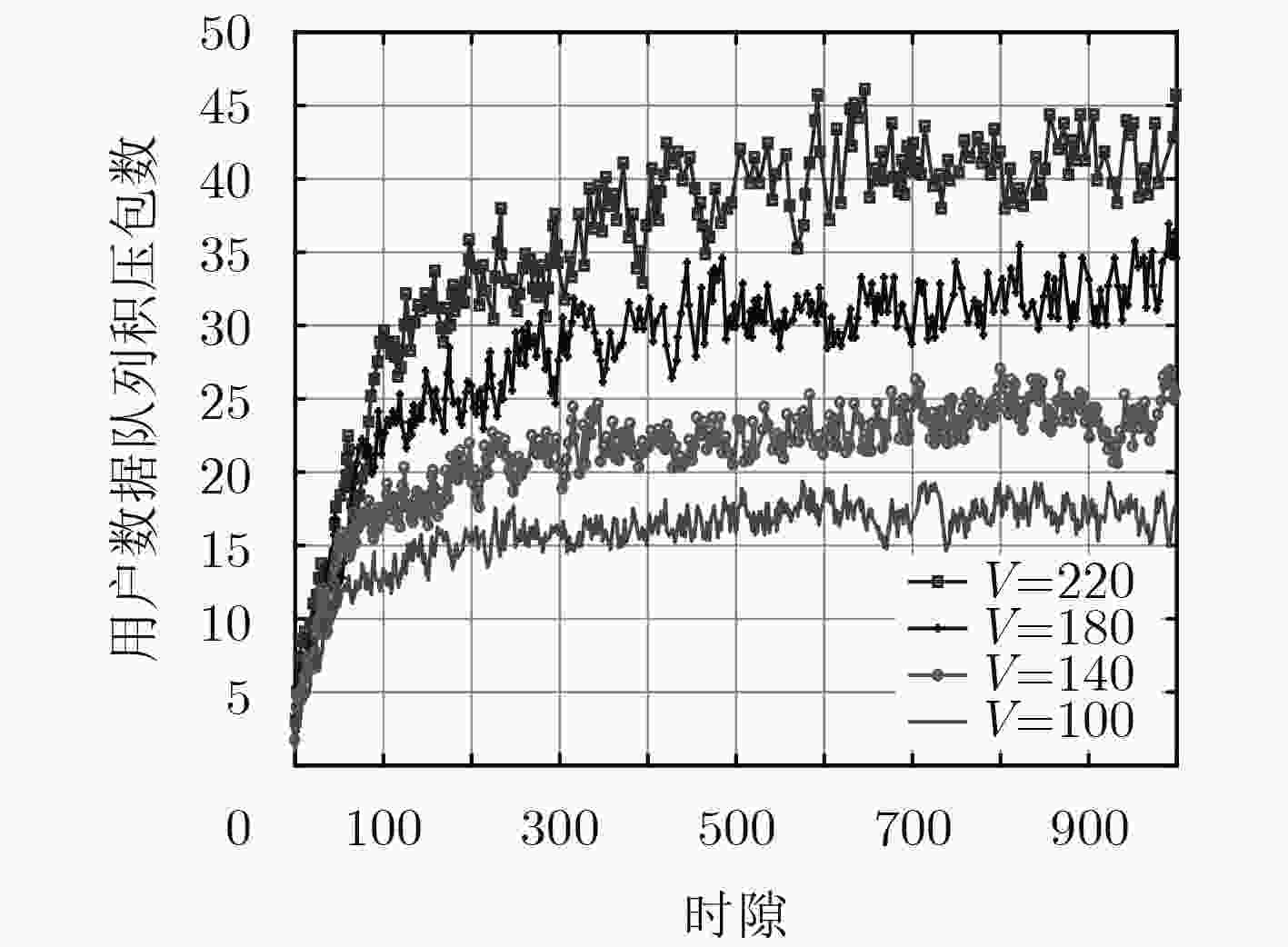
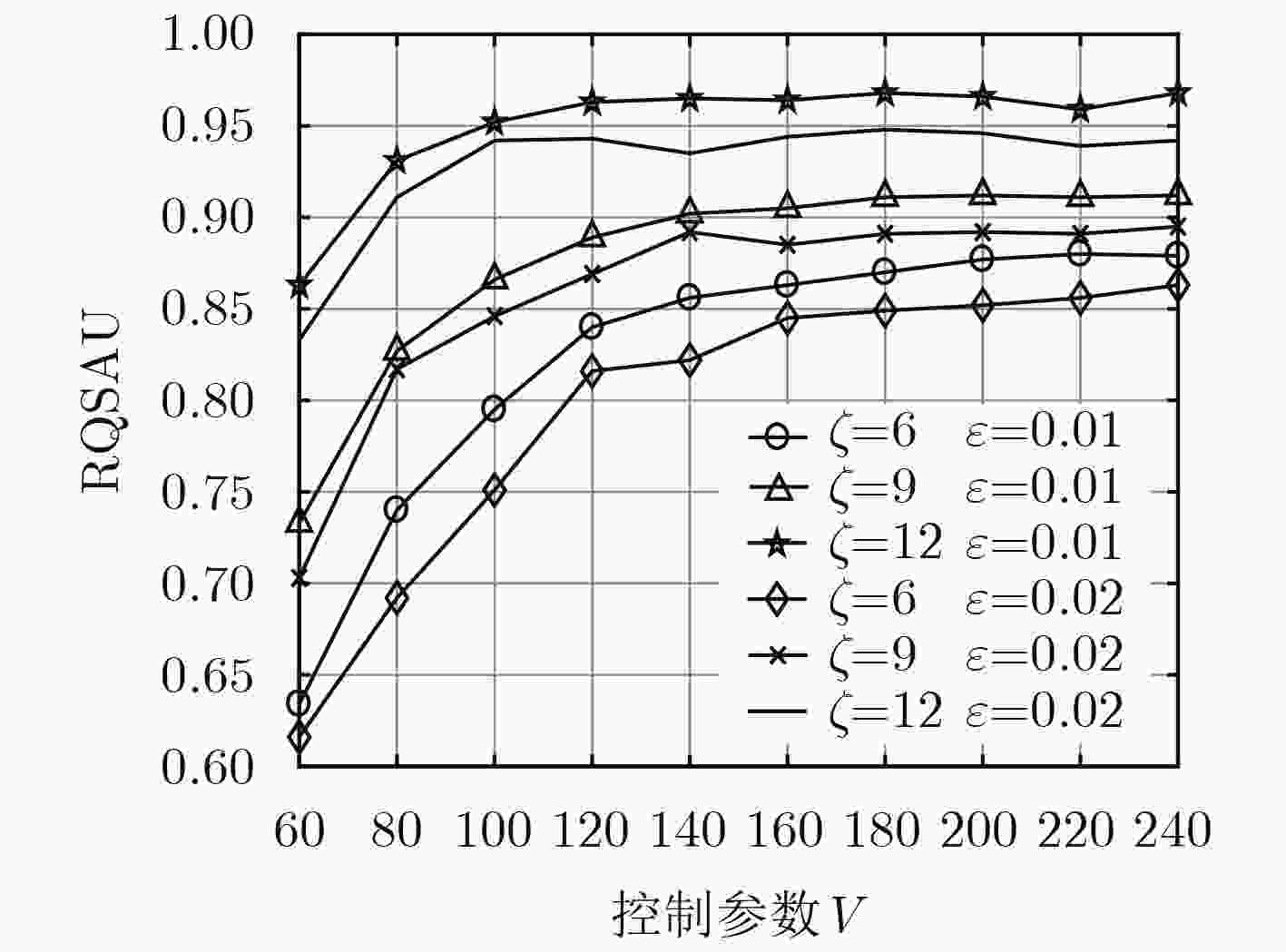
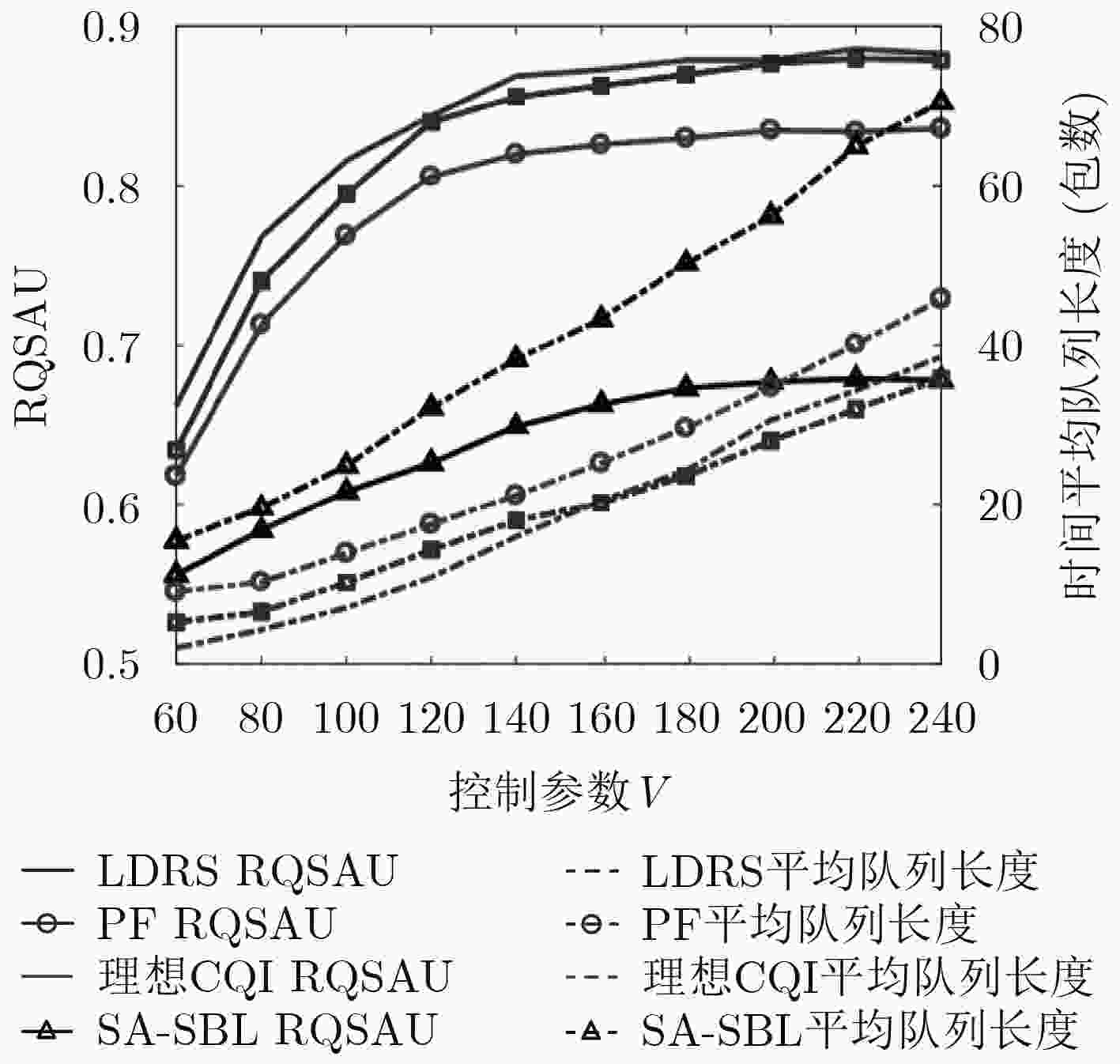
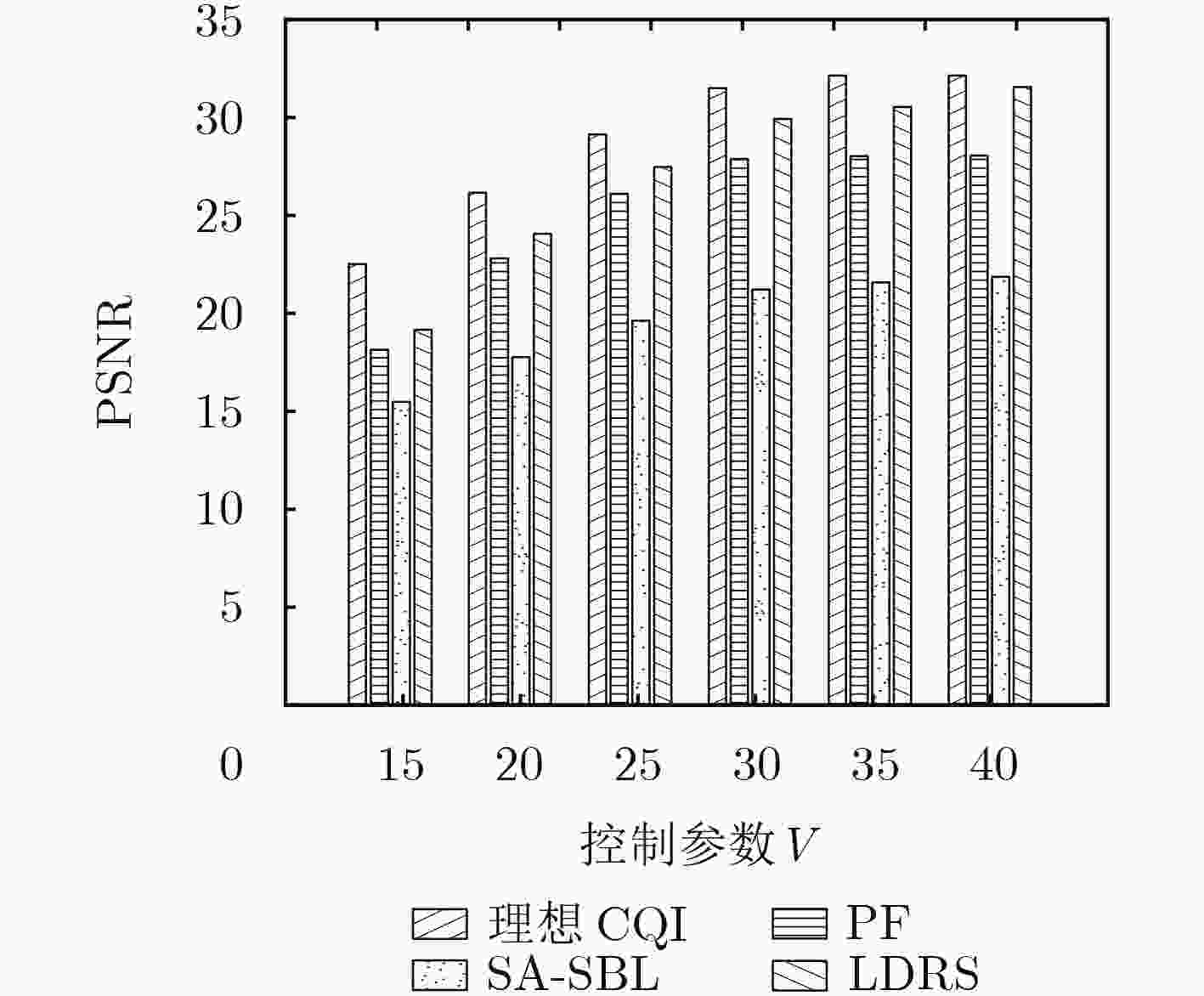
摘要: 针对接入与回传一体化小基站场景下用户个性化视频流业务需求问题，该文提出一种基于接入与回传一体化小基站的用户满意度最大化算法。该算法首先根据系统实际可达速率和用户满意度需求速率间的不匹配程度，动态调整下一周期队列传输所需频谱资源，并建立用户质量满意度最大化模型，其次运用Lyapunov优化方法把初始问题转化为Lyapunov偏移加罚项的优化，将溢出概率约束转化为关于自变量的不等式，最后基于拉格朗日对偶分解的用户接入带宽分配算法和基于内点法的回传和接入带宽分配算法进行求解。仿真结果表明，该算法提高了系统用户质量满意度，同时保证了系统稳定性。
- 接入与回传一体化小基站 /
- 视频流业务 /
- 用户质量满意度 /
- 李雅普诺夫优化方法
Abstract: To meet the personal quality requirement of video streaming service under the access and backhaul integrated small base station scene, a user satisfaction maximization algorithm is proposed. The algorithm adjusts dynamically the spectrum resources used for next-cycle queue transmission by analysis the mismatch degree between the actual system reachable rate and user satisfaction demand rate. The corresponding optimization model of the quality satisfaction of all users is established. Then, the Lyapunov stochastic optimization method is used to transform the initial problem into drift plus penalty, the overflow probability constraint is transformed into inequality of variables. Finally, using the proposed user access bandwidth allocation algorithm based on Lagrange dual decomposition and the backhaul and access bandwidth allocation algorithm based on interior point method. The simulation results show that the algorithm can improve the quality satisfaction of all users and ensure the system stability.
- Access and backhaul integrated small base station /
- Video streaming /
- Quality satisfaction of all users /
- Lyapunov-based optimization

HTML全文

1. 引言

电磁频谱监测^[1]是实现无线电管理的技术手段之一。随着通信技术发展和应用普及，无线电频谱管理工作越来越复杂，为更加高效管理无线电资源，避免未知信号源对现有电磁环境干扰，根据频谱监测数据及时对信号进行定位和跟踪一直是电磁频谱研究热点之一。

对信号源定位技术主要有以下几种实现方法，例如信号到达时间差(TDOA)^[2—6]、信号到达角度(AOA)^[5,6]、信号到达频率差(FDOA)^[7,8]以及接收信号强度指示(RSSI)^[9—11]等。其中TDOA, AOA, FDOA及其联合定位的定位精度较高，但需要监测设备拥有额外的硬件^[10]。综合考虑，在频谱监测系统中频谱数据所包含的信号相关参数较少，且地面监测站接收机并没有都配备昂贵的测向设备等特点，因而RSSI定位技术是目前频谱监测中一种比较有效的方法。

由于被监测信号无法控制且没有任何先验知识，只能通过对信号的被动监测，即接收与处理信号来估计信号源位置的情况，无法直接利用RSSI测距定位。本文提出了一种新的定位算法，即将监测站间的接收信号强度指示差值(RSSID)转换成信号源到两监测站的距离之比进行定位。此外，在已知信号源到监测站距离的情况下，距离之比定位(Localization with Ratio-Distance, LRD)比三边测量法(Trilateration)具有更加优越的定位性能^[12]。结合LRD思想，本文提出了一种适用于频谱监测系统对信号源进行有效定位的方法，即RSSID定位算法。

2. 定位原理

2.1 RSSI值求取距离之比

在研究信号源位置估算方法之前，有必要选择一种适合当前环境的无线电波传播的数学模型。本文采用适合解决市区无线电信号源位置估计的Egli电波传播模型^[13]，其经验公式如式(1)所示。

$L = 78 + 20\lg f + 40\lg d - 20{h_t} - 20{h_r}$

(1)

式中， $L$ 为路径衰减，单位dB； $f$ 为信号频率，单位MHz； $d$ 为信号源到监测站的距离，单位km； ${h_t}$ 为信号源发射天线高度，单位m； ${h_r}$ 监测站接收天线的高度，单位m。

发射功率与接收功率之间的关系为

${\rm{RSSI}} = {P_t} - L$

(2)

式中，RSSI为监测站接收功率，单位dB； ${P_t}$ 为信号源发射功率，单位dB。

为了消除信号源的相关参数，通过式(3)消去信号源发射天线高度 ${h_t}$ 以及信号源发射功率 ${P_t}$ 。

${\rm{RSS}}{{\rm{I}}_0} - {\rm{RSS}}{{\rm{I}}_i} = {L_i} - {L_0} = 40\lg \frac{{{d_i}}}{{{d_0}}} + 20\lg \frac{{{h_{{\rm{r}}0}}}}{{{h_{{\rm{ri}}}}}}$

(3)

式中， ${\rm{RSS}}{{\rm{I}}_0}$ 为主监测站接收功率， ${\rm{RSS}}{{\rm{I}}_i}$ 为第 $i$ 个次监测站接收功率，因此信号源到各次监测站距离与到主监测站的距离之比 ${k_{{\rm{i}}0}}$ 为

${k_{{\rm{i}}0}} = \frac{{{d_i}}}{{{d_0}}} = {10^{\frac{{{\rm{RSS}}{{\rm{I}}_0} - {\rm{RSS}}{{\rm{I}}_i} - 20\lg \frac{{{h_{{\rm{r}}0}}}}{{{h_{{\rm{ri}}}}}}}}{{40}}}}$

(4)

2.2 根据距离之比定位

由解析几何可知，信号源到两个监测站的距离之比(比值不等于1)为常数时，其轨迹是一个圆，此圆的圆心位于两监测站位置的连线上并且靠近接收信号大的监测站一侧。假设有3个监测站同时接收到同一信号电平，就可以得到2个距离比圆，得到2个可能的信号源位置解，再根据信号源辐射范围即可确定信号源位置。

设主监测站位置为 ${B_0}\left( {{x_0},{y_0}} \right)$ ，接收天线的高度为 ${h_0}$ ，次监测站位置为 ${B_1}\left( {{x_1},{y_1}} \right)$ , ${B_2}\left( {{x_2},{y_2}} \right)$ ，接收天线高度分别为 ${h_1}$ , ${h_2}$ ，信号源的实际位置为 $S\left( {{x_s},{y_s}} \right)$ ，两个距离比圆的圆心为 ${C_1}\left( {{x_{{\rm{c}}1}},{y_{{\rm{c}}1}}} \right)$ , ${C_2}$ $\left( {{x_{{\rm{c}}2}},{y_{{\rm{c}}2}}} \right)$ ，所以根据距离之比和已知监测站位置，可得到

$\begin{aligned} {k_{{\rm{i}}0}} & = 1{0^{\frac{{{\rm{RSS}}{{\rm{I}}_0} - {\rm{RSS}}{{\rm{I}}_i} - 20\lg \frac{{{h_{{\rm{r}}0}}}}{{{h_{{\rm{ri}}}}}}}}{{40}}}} = \frac{{{d_i}}}{{{d_0}}}\\ & = \frac{{\sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}} }}{{\sqrt {{{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}} }} = \sqrt {{\lambda _i}} \;,\;\; {i = 1,2} \end{aligned}$

(5)

整理式(5)得

$\begin{aligned} & {\left( {x - \frac{{{x_i} - {\lambda _i}{x_0}}}{{1 - {\lambda _i}}}} \right)^2} + {\left( {y - \frac{{{y_i} - {\lambda _i}{y_0}}}{{1 - {\lambda _i}}}} \right)^2} \\ & = \frac{{{\lambda _i}}}{{{{\left( {1 - {\lambda _i}} \right)}^2}}}\left[ {{{\left( {{x_0} - {x_i}} \right)}^2} + {{\left( {{y_0} - {y_i}} \right)}^2}} \right] \\ & = \frac{{{\lambda _i}}}{{{{\left( {1 - {\lambda _i}} \right)}^2}}}d_{{\rm{i}}0}^2 \end{aligned}$

(6)

式(6)中， ${d_{{\rm{i}}0}}$ 为次监测站到主监测站的距离，可以得到距离比圆的信息。圆心坐标为

${x_{{\rm{ci}}}} = \frac{{{x_i} - {\lambda _i}{x_0}}}{{1 - {\lambda _i}}},\;\;{y_{{\rm{ci}}}} = \frac{{{y_i} - {\lambda _i}{y_0}}}{{1 - {\lambda _i}}}$

(7)

距离比圆半径：

${R_i} = \left| {\frac{{{k_{{\rm{i}}0}}}}{{1 - {\lambda _i}}}} \right|{d_{{\rm{i}}0}}$

(8)

因此，至少使用3个监测站才可得到2个距离比圆，两圆在监测站共同覆盖范围的交点即为目标位置。实际情况中，多个监测站进行监测时，可以得到多个距离比圆，由于误差的存在，多个距离比圆相交将产生多个可能的目标解，式(9)对应的目标序号 $j$ 即为所要求的目标解：

$\min \!\left[ {\sum\limits_{i = 0}^n {\sqrt {{{\left( {{x_i} - {x_j}} \right)}^2} \!+\! {{\left( {{y_i}\! -\! {y_j}} \right)}^2}} } } \right],\;\;j \in \!\left[ {0,n \!-\! 1} \right] \hspace{10pt}$

(9)

本文算法的定位原理如图1所示。

图 1 RSSID定位原理图

下载: 全尺寸图片幻灯片

3. 算法步骤

3.1 数据预处理

从式(4)可以看出，信号源到次监测站与主监测站的距离之比与RSSI信号密切相关。但是，在信号的实际传播过程中RSSI信号容易受到电波传播环境影响，例如障碍物尺寸、天气的好坏以及接收节点所在位置的高度等，因此，需要对RSSI信号进行预处理得到平稳变化的RSSI信号。

卡尔曼滤波是基于线性最小均方误差预测和线性递归更新的优化算法^[14]，根据前一时刻的预测值和当前时刻的测量值更新当前时刻的预测值，可以有效解决干扰噪声服从正态分布的滤波问题，适用于RSSI信号的滤波处理^[15—18]。在这项工作中，RSSI信号噪声被假定为高斯噪声，虽然这个假设并不完全准确，但实际测量中RSSI值的误差波动比较集中，此时卡尔曼滤波器可以在一定程度上解决信号漂移和冲击问题^[18]。其次，卡尔曼滤波在求解时不需要储存大量的观测数据，并且当得到新的观测数据时，可随时算得新的参数滤波值，便于实时地处理观测数据。

对RSSI信号进行“测量-预测-更新”，消除系统随机噪声，平滑RSSI信号。主要包括两个阶段：预测和更新。预测阶段为^[16]

$k$ 时刻状态预测：

$x\left( {k\left| {k - 1} \right.} \right) = x\left( {k - 1\left| {k - 1} \right.} \right)$

(10)

协方差预测：

$P\left( {k\left| {k - 1} \right.} \right) = P\left( {k - 1\left| {k - 1} \right.} \right) + Q$

(11)

式中， $x\left( {k - 1\left| {k - 1} \right.} \right)$ 为 $k - 1$ 时刻RSSI信号的状态值， $x\left( {k\left| k \right.} \right)$ 为 $k$ 时刻RSSI信号的状态值， $x\left( {k\left| {k - 1} \right.} \right)$ 为 $k$ 时刻RSSI信号的预测值， $P\left( {k - 1\left| {k - 1} \right.} \right)$ 是对应 $x\left( {k - 1\left| {k - 1} \right.} \right)$ 的系统误差协方差， $P\left( {k\left| {k - 1} \right.} \right)$ 对应 $x\left( {k\left| {k - 1} \right.} \right)$ 的系统误差协方差， $Q$ 状态噪声协方差。递归估计更新阶段^[16]：

卡尔曼增益：

${\rm{Kg}}\left( k \right) = \frac{{P\left( {k\left| {k - 1} \right.} \right)}}{{P\left( {k\left| {k - 1} \right.} \right) + R}}$

(12)

$k$ 时刻状态更新：

$x\left( {k\left| k \right.} \right) \!=\! x\left( {k\left| {k \!-\! 1} \right.} \right) \!+\! {\rm{Kg}}\left( k \right)\left[ {y\left( k \right) \!-\! x\left( {k\left| {k - 1} \right.} \right)} \right] \hspace{15pt}$

(13)

协方差更新：

$P\left( {k\left| {k - 1} \right.} \right) = \left( {1 - {\rm{Kg}}\left( k \right)P\left( {k\left| {k - 1} \right.} \right)} \right)$

(14)

式中， $R$ 是测量噪声协方差， ${\rm{Kg}}\left( k \right)$ 是 $k$ 时刻的卡尔曼增益， $y\left( k \right)$ 是 $k$ 时刻RSSI信号的测量值。当对象模型足够准确且系统状态和参数不发生突变时，卡尔曼滤波性能较好。

3.2 定位算法

实际使用中发现，监测站距离信号源较近时，由于受到传播路径的影响较小， ${\rm{RSSI}}$ 测量值相对较准确^[19]，因此选取 ${\rm{RSSI}}$ 值最大的监测站作为主监测站。根据式(5)可以求得信号源到其余各监测站与主监测站的距离之比。

另外由信号源 $S\left( {{x_s},{y_s}} \right)$ 到达监测站 ${B_i}\left( {{x_i},{y_i}} \right)$ , $i = 1,2, ·\!·\!· ,N + 1$ 的欧式距离公式可得

$k_{{\rm{i}}0}^2 \!=\! \frac{{d_i^2}}{{d_0^2}} \!=\! \frac{{{{\left\| {S - {B_i}} \right\|}^2}}}{{{{\left\| {S - {B_0}} \right\|}^2}}} = \frac{{{{\left( {{x_s} - {x_i}} \right)}^2} \!+\! {{\left( {{y_s} - {y_i}} \right)}^2}}}{{{{\left( {{x_s} \!-\! {x_0}} \right)}^2} + {{\left( {{y_s} - {y_0}} \right)}^2}}}$

(15)

将式(15)整理展开可以得到

$\begin{aligned} & \left( {1 \!-\! k_{{\rm{i}}0}^2} \right)\!\!\left( {{x_s}\!\!^2 \!+\! {y_s}\!\!^2} \right) \!+\! 2\left( {k_{{\rm{i}}0}^2{x_{\rm{0}}} \!-\! {x_i}} \right){x_s} \!+\! 2\left( {k_{{\rm{i}}0}^2{y_{\rm{0}}} \!-\! {y_i}} \right){y_s} \\ & \quad\quad\quad\ = k_{{\rm{i}}0}\!\!^2\left( {{x_{\rm{0}}}\!\!^2 + {y_{\rm{0}}}\!\!^2} \right) - {x_i}\!\!^2 - {y_i}\!\!^2 \end{aligned}$

(16)

设 ${{S}}' = \left[ {{x_s},{y_s},{x_s}\!\!^2 + {y_s}\!\!^2} \right]$ 为未知矢量建立方程， $N$ 个上述方程构成定位矩阵：

${{GS}}' = {{b}}$

(17)

式中，

${{G}} =\!\! \left[\! \begin{array}{l} \begin{array}{*{20}{c}} \!\!{2\left( {k_{10}^2{x_0} - {x_1}} \right)} & {2\left( {k_{10}^2{y_0} - {y_1}} \right)} & {1 - k_{10}^2}\!\!\!\!\\ \!\!{2\left( {k_{20}^2{x_0} - {x_2}} \right)} & {2\left( {k_{20}^2{y_0} - {y_2}} \right)} & {1 - k_{20}^2}\!\!\!\!\\ \!\! \vdots & \vdots & \vdots \!\!\!\! \end{array}\\ \begin{array}{*{20}{c}} \!\!{2\left( {k_{N0}^2{x_0} - {x_N}} \right)} & {2\left( {k_{N0}^2{y_0} - {y_N}} \right)} & {1 - k_{10}^2}\!\!\!\! \end{array} \end{array} \!\right]\!,\;\;\\ {{b}} = \left[ {\begin{array}{*{20}{c}} {k_{10}^2\left( {x_0^2 + y_0^2} \right) - x_1^2 - y_1^2}\\ {k_{20}^2\left( {x_0^2 + y_0^2} \right) - x_2^2 - y_2^2}\\ \vdots \\ {k_{N0}^2\left( {x_0^2 + y_0^2} \right) - x_N^2 - y_N^2} \end{array}} \right]$

(18)

于是得到了 ${{S}}'$ 的最小二乘估计值：

${{S}}' = {\left( {{{{G}}^{\rm{T}}}{{G}}} \right)^{ - 1}}{{{G}}^{\rm{T}}}{{b}}$

(19)

则信号源位置 ${{S}} = {{S}}'[1:3]$ 。

4. 计算机仿真

本文使用Java编程实现RSSI和RSSID定位算法的仿真实验，并利用Python语言对实验结果进行了分析和处理。本文算法已使用Java编程成功应用于国内某频谱大数据监测平台。

为分析本文算法的定位性能，在相同的仿真环境下进行以下仿真分析实验。仿真环境设置为4个监测站，分别位于20 km×20 km的正方形区域的4个顶点上，其坐标为(0, 0), (0, 20), (20, 0)和(20, 20)。另外，为对比本文算法与RSSI测距定位算法的定位性能，以下实验中已知信号源的相关参数，如频率、发射天线高度及发射功率等。

4.1 影响因素分析

分别验证接收信噪比SNR以及监测站间距对定位精度的影响，采用定位结果与真实值之间的均方根误差衡量定位精度，

${\rm{RMSE}}\left( u \right) =\frac{{ \displaystyle\sum\limits_{i = 0}^N {\left\| {{u_{{\rm{obj}},i}} - {u_{{\rm{mea}},i}}} \right\|} }}{N}$

(20)

其中， $N$ 是信号源个数， ${u_{{\rm{obj}},i}}$ 表示第 $i$ 个信号源的真实位置， ${u_{{\rm{mea}},i}}$ 表示 $i$ 个信号源的定位结果。参与比较的算法包括：传统RSSI定位算法，本文所提的RSSID定位算法。

4.1.1 接收信噪比SNR对定位精度的影响

为验证接收信噪比SNR对定位精度的影响，在相同的监测站位置配置下比较不同定位算法的定位性能，设置区域内随机点数 $N = 400$ ，接收信噪比SNR∈[–16, 20] dB。

定位精度随信噪比不同的变化情况如图2所示，对比传统RSSI定位算法，当SNR∈[0, 20] dB时本文算法性能明显提升，这是因为即使估计的距离与真实距离相差较大，距离的比例也没有太大的影响。当SNR≤–4 dB时，噪声在接收信号中起决定性作用，本文算法与RSSI定位算法误差均较大，无法正确估计信号源位置；当SNR≥–4 dB时，本文算法定位性能优于RSSI定位算法。

图 2 随信噪比变化的定位性能

下载: 全尺寸图片幻灯片

4.1.2 监测站间距对定位精度的影响

为验证监测站间距对定位精度的影响，设置信噪比SNR=16 dB，监测区域内信号源个数 $N = 1000$ ，监测站间距 $d \in [1,20]$ km。

定位精度随监测站间距不同的变化情况如图3所示，对比传统RSSI定位算法，随着监测站间距的增大，本文算法定位误差明显较小，性能明显提升。

图 3 随监测站间距变化的定位性能

下载: 全尺寸图片幻灯片

4.2 RSSI定位与RSSID定位误差分析

在此分析监测站接收信号信噪比为SNR=16 dB时，RSSID定位与RSSI定位的定位性能，以及卡尔曼滤波算法对RSSID定位的优化能力。

4.2.1 数据预处理

RSSID定位与RSSI定位的定位精度均受到信号接收强度的影响，因此有必要对RSSI信号进行预处理。本文采用卡尔曼滤波处理RSSI信号，如图4(a)与图4(b)所示，卡尔曼滤波可以实现对RSSI信号的平滑处理，减少RSSI信号的测量误差。

图 4 卡尔曼滤波效果图

下载: 全尺寸图片幻灯片

4.2.2 单目标定位

为对比RSSID定位算法与RSSI定位算法对单个目标的定位性能，对区域内随机一个目标进行200次定位。两种不同算法的定位误差如图5(a)与图5(b)所示，可以看出滤波前后，RSSID定位算法与RSSI定位算法都可以对信号源进行有效定位，RSSID定位算法均比RSSI定位算法定位误差较小。

图 5 单目标定位误差对比

下载: 全尺寸图片幻灯片

为了避免仿真实验的随机性，对1个随机生成的信号源进行10000次定位，分析其误差，如表1所示。

表 1 单目标定位10000次误差统计分析(km)

是否预处理	定位方法	最大误差	最小误差	平均误差
否	RSSI定位	5.0802	0.0239	1.3993
否	RSSID定位	4.6224	0.0076	0.8527
是	RSSI定位	1.4537	0.2273	0.6249
是	RSSID定位	0.8801	0.0068	0.2683

下载: 导出CSV

| 显示表格

4.2.3 多目标定位

为对比RSSID定位算法与RSSI定位算法对多个目标同时定位的定位性能，对区域内随机生成的25个信号源进行200次定位。两种不同算法的定位误差如图6(a)与图6(b)所示，可以看出滤波前后，本文RSSID算法定位性能均明显优于RSSI定位算法。

图 6 多目标定位平均误差对比

下载: 全尺寸图片幻灯片

为避免因为数据量较少出现偶然误差，对200个信号源进行10000次定位，分析每次对200个信号源定位的平均误差，统计结果如表2所示。

表 2 多目标定位10000次平均误差统计分析(km)

是否预处理	定位方法	最大误差	最小误差	平均误差
否	RSSI定位	1.8602	1.3599	1.5911
否	RSSID定位	1.1015	0.7620	0.9170
是	RSSI定位	1.5312	0.9470	1.1530
是	RSSID定位	0.8284	0.1948	0.2930

下载: 导出CSV

| 显示表格

5. 结束语

本文提出了一种运用于频谱监测系统对监测信号有效定位的方法。在频谱监测系统中，被监测信号无法控制并且没有任何先验知识，只能通过对信号的被动监测、接收与处理来估计信号源的位置，此时不适用传统RSSI定位法，而本文RSSID算法是根据监测站地理位置以及各监测站接收信号强度对信号源定位的，不需要任何先验知识。因此，本文算法适用性更广，可用于频谱监测系统对监测到的未知信号进行实时定位。

仿真分析表明，在信号相关参数已知的情况下，本文RSSID算法比传统RSSI定位法受到信噪比的影响较小，定位性能更加优越。另外引入卡尔曼滤波对RSSI值进行预处理可以极大的提高本文算法的定位性能。

图 1 系统场景图

下载: 全尺寸图片幻灯片

图 2 虚拟队列积压

下载: 全尺寸图片幻灯片

图 3 用户在连续时隙上的队列积压

下载: 全尺寸图片幻灯片

图 4 RQSAU与控制参数V 的关系

下载: 全尺寸图片幻灯片

图 5 不同资源分配方案的平均队列积压比较

下载: 全尺寸图片幻灯片

图 6 不同资源分配方案的RQSAU和队列稳定性比较

下载: 全尺寸图片幻灯片

图 7 不同资源分配方案的PSNR比较

下载: 全尺寸图片幻灯片

表 1 基于拉格朗日对偶分解的用户接入带宽分配算法

　算法1 基于拉格朗日对偶分解的用户接入带宽分配算法

　步骤1 初始化

${{{π}} ^{(0)}},{o^{(0)}},{\delta ^{(0)}},{\sigma ^{(0)}}$ ,

$\beta = 0.1$ ，终止条件

${\varDelta _1} = {10^{ - 2}}$ ；

　步骤2 根据

${\rm{P}}2.2$ 式(28)求计算UE接入带宽分配

${\eta _{1,k}}$ 的表达式；

　步骤3 判定式

$||{Y^{(n + 1)}}(t) - {Y^{(n)}}(t)|| \le {\varDelta _1}$ ，若满足，则执行步骤
　　　　6，否则执行步骤4；

　步骤4 根据梯度法更新对偶变量

${{{π}} ^{(n)}},{o^{(n)}},{\delta ^{(n)}},{\sigma ^{(n)}}$ ；

　步骤5

$n = n + 1$ ，将更新的拉格朗日乘子值代入

${\rm P}2.2$ 式(28)中计
　　　　算，得到新的用户接入频带分配比例，并跳转步骤3；

　步骤6 获得UE接入带宽分配方案

${\eta _{1,k}}\!\!\!\!^*\$ 。

下载: 导出CSV

表 2 基于内点法的回传和接入带宽分配算法

　算法2 基于内点法的回传和接入带宽分配算法
　步骤1 取初始

${\chi ^{\left( 0 \right)}},{\rho ^{\left( 0 \right)}},{\kappa ^{\left( 0 \right)}},{\omega ^{\left( 0 \right)}}$ 都>0，一般取各自初始值为1，
误差

${\varDelta _2} = {10^{ - 3}} > 0$ ；
　步骤2 用随机数生成法生成多个初始点，并选取满足约束条件的
　　　　初始点

${\beta ^{(0)}}$ ，令

$n = 1$ ；
　步骤3 构造惩罚函数

$\varphi \left( {\beta ,{\chi ^{(n)}},{\rho ^{(n)}},{\kappa ^{(n)}},{\varpi ^{(n)}}} \right)$ ，从

${\beta ^{(n - 1)}}$ 点出发
　　　　用无约束优化方法求惩罚函数的极值点：
　　　　　　　　

${\beta ^*}\left( {{\chi ^{(n)}},{\rho ^{(n)}},{\kappa ^{(n)}},{\varpi ^{(n)}}} \right)$
　步骤4 检查迭代终止准则：如果满足
　　　　　　

$\left|\frac{{\varDelta \varphi }}{{\varphi \left( {{\beta ^*},{\chi ^{(n - 1)}},{\rho ^{(n - 1)}},{\kappa ^{(n - 1)}},{\varpi ^{(n - 1)}}} \right)}}\right| \le {\varDelta _2}$
其中，
　　　　　　

$\begin{align} \Delta \varphi =& \varphi \left( {{\beta ^*},{\chi ^{(n)}},{\rho ^{(n)}},{\kappa ^{(n)}},{\varpi ^{(n)}}} \right) \\ &- \varphi \left( {{\beta ^*},{\chi ^{(n - 1)}},{\rho ^{(n - 1)}},{\kappa ^{(n - 1)}},{\varpi ^{(n - 1)}}} \right) \\ \end{align}$
则停止迭代计算，并以

$\left( {{\beta ^*},{\chi ^{(n)}},{\rho ^{(n)}},{\kappa ^{(n)}},{\varpi ^{(n)}}} \right)$ 作为
目标函数P2.3的局部最优解，否则转步骤5；
　步骤5 缩小惩罚因子，

$n = n + 1$ ，转向步骤3。递减系数
　　　　

${\omega _1},{\omega _2},{\omega _3},{\omega _4}$ 通常取值为0.1。

下载: 导出CSV

表 3 基于接入与回传一体化小基站的用户满意度最大化全局算法

　算法3 基于接入与回传一体化小基站的用户满意度最大化全局算法

　步骤1 初始化带宽分配比例

$\beta$ 和误差

$\varDelta = {10^{ - 5}}$ ；

　步骤2 根据式(27)求子问题

${\rm{P}}2.1$ UE回传带宽分配方案的局部最优解

${\mu _k}\!\!^*$ ；

　步骤3 根据算法1求问题

${\rm{P}}2.2$ 每个用户的接入带宽分配方案的局部最优

${\eta _{1,k}}\!\!\!\!^*\$ ；

　步骤4 将最优解

${\mu _k}\!\!^*$ 与最优解

${\eta _{1,k}}\!\!\!\!^*\$ 代入式(26)，根据算法2求问题

${\rm{P}}2.3$ 回传带宽分配比例的局部最优解

${\beta^*}$ ；
　步骤5 将

${\mu _k}\!\!^*$ 与

${\eta _{1,k}}\!\!\!\!^*\ ,{\beta ^*}$ 代入到最初目标问题P2中，检查收敛条件

$\left\| {f\left( {\eta _{1,k}^{(n)}(t),\mu _k^{(n)}(t),{\beta ^{(n)}}(t)} \right) - f\left( {\eta _{1,k}^{(n - 1)}(t),\mu _k^{(n - 1)}(t),{\beta ^{(n - 1)}}(t)} \right)}\right\| \le \varDelta$ 是否
　　　　满足，否则令

$\beta = {\beta ^*}$ ，并依此执行步骤2

$\sim$ 步骤5；当满足收敛条件，则获得最初问题

${\rm P}2$ 的全局最优解

${\beta ^*}$ ,

${\eta _{1,k}}\!\!\!\!^*\$ 和

${\mu _k}\!\!^*$ 。

下载: 导出CSV

表 4 仿真参数

参数	数值	参数	数值
载波频率	3.5 GHz	总用户数	15
天线阵列数 ${K_T}$	100	波束成形组大小 ${K_g}$	20
噪声功率谱密度 ${N_0}$	–174 dBm/Hz	宏基站天线模型	MIMO波束赋形^[6]
宏基站发送功率 ${P_0}$	46 dBm	天线阵列数目是 ${K_T}$	100
小基站发送功率 ${P_{}}$	33 dBm	业务相关系数 $\zeta$	6, 9, 12
用户业务模型	到达率1 packet/slot	业务质量需求U^E	30, 45, 60

下载: 导出CSV

参考文献(13)

JABER M, IMRAN M A, TAFAZOLLI R, et al. 5G backhaul challenges and emerging research directions: A survey[J]. IEEE Access, 2017, 4: 1743–1766 doi: 10.1109/ACCESS.2016.2556011

GE Xiaohu, TU Song, MAO Guoqiang, et al. 5G ultra-dense cellular networks[J]. IEEE Wireless Communications, 2016, 23(1): 72–79 doi: 10.1109/MWC.2016.7422408

ROBSON J. Small cell backhaul requirements[R]. A White Paper by the NGMN Alliance, Cambridge: NGMN, 2012.

SIDDIQUE U, TABASSUM H, and HOSSAIN E. Adaptive in-band self-backhauling for full-duplex small cells[C]. IEEE International Conference on Communication Workshop, London, UK, 2015: 44–49.

TAORI R, and SRIDHARAN A. Point-to-multipoint in-band mmwave backhaul for 5G networks[J]. IEEE Communications Magazine, 2015, 53(1): 195–201 doi: 10.1109/MCOM.2015.7010534

WANG Ning, HOSSAIN E, BHARGAVA V K. Joint downlink cell association and bandwidth allocation for wireless backhauling in two-tier hetNets with large-scale antenna arrays[J]. IEEE Transactions on Wireless Communications, 2016, 15(5): 3251–3268 doi: 10.1109/TWC.2016.2519401

NEELY Michael. Stochastic Network Optimization with Application to Communication and Queueing Systems[M]. San Rafael, USA: Morgan & Claypool, 2010: 149–152.

CHEN Lei, YU F. Green full-duplex self-backhaul and energy harvesting small cell networks with massive MIMO[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3709–3724 doi: 10.1109/JSAC.2016.2611846

XU Yiran, Hu Rose Qiyang, QIAN Yi, et al. Video quality-based spectral and energy efficient mobile association in heterogeneous wireless networks[J]. IEEE Transactions on Communications, 2016, 64(2): 805–817 doi: 10.1109/TCOMM.2015.2503760

LAKSHMINARAYANA S, ASSAAD M, and DEBBAH M. Transmit power minimization in small cell networks under time average QoS constraints[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(10): 2087–2103 doi: 10.1109/JSAC.2015.2435312

LIU Yinjun, LU Lu, LI Geoffrey Ye, et al. Joint user association and spectrum allocation for small cell networks with wireless backhauls[J]. IEEE Wireless Communications Letters, 2017, 5(5): 496–499 doi: 10.1109/LWC.2016.2593465

HUANG Jianwei, SUBRAMANIAN V, AGRAWAL R, et al. Downlink scheduling and resource allocation for OFDM systems[C]. 2006, IEEE International Conference on Information Sciences and Systems, Princeton, USA, 2007: 288–296.

YUN H C, KIM H, LEE S H, et al. A QoE-aware proportional fair resource allocation for multi-cell OFDMA networks[J]. IEEE Communications Letters, 2015, 19(1): 82–85 doi: 10.1109/LCOMM.2014.2367115

施引文献

期刊类型引用(12)

1.	余修武，彭威，余员琴，刘永. 基于SSO的铀尾矿库无线传感器网络定位算法. 中国安全科学学报. 2023(04): 84-90 . 百度学术
2.	束仁义，朱家兵，沈晓波，蔡俊，夏泐. 基于KF-BA-LSSVR的无线传感器网络节点定位研究. 重庆科技学院学报(自然科学版). 2022(03): 57-61 . 百度学术
3.	吴红生，黄良永. 激光传输过程中的信号捕获与自动跟踪研究. 激光杂志. 2022(07): 139-143 . 百度学术
4.	路韬，黄友朋，党三磊，张捷. 基于改进ELM的计量终端定位算法仿真. 计算机仿真. 2022(09): 377-383 . 百度学术
5.	林逢春，谭文武. 人工智能技术的高速光纤通信链路智能选择研究. 激光杂志. 2022(12): 159-163 . 百度学术
6.	赵书红，董绍武，白杉杉，高喆. 一种优化的频率驾驭算法研究. 电子与信息学报. 2021(05): 1457-1464 . 本站查看
7.	张旭，姚善化. 未调制可见光室内定位. 湖南文理学院学报(自然科学版). 2021(03): 58-61+80 . 百度学术
8.	孙小君，周晗，沈海滨，闫广明. 加权融合鲁棒增量Kalman滤波器. 电子与信息学报. 2021(12): 3680-3686 . 本站查看
9.	郭永宁，李燕龙. 无人机无线电监测混合定位算法. 桂林电子科技大学学报. 2021(05): 362-367 . 百度学术
10.	梁拥军. 基于卡尔曼滤波的无线电台电磁干扰源定位方法研究. 电子设计工程. 2020(09): 112-116 . 百度学术
11.	孙小君，周晗，闫广明. 基于新息的自适应增量Kalman滤波器. 电子与信息学报. 2020(09): 2223-2230 . 本站查看
12.	康颜爽，苏胜君，施伟斌，乐燕芬，韩承毅. 一种基于核岭回归与卡尔曼滤波的定位算法. 软件导刊. 2020(09): 74-77 . 百度学术

其他类型引用(16)

资源附件(0)

访问统计

图(7) / 表(4)

计量

文章访问数: 3107
HTML全文浏览量: 618
PDF下载量: 43
被引次数: 28

1. 引言
2. 定位原理
2.1 RSSI值求取距离之比
2.2 根据距离之比定位
3. 算法步骤
3.1 数据预处理
3.2 定位算法
4. 计算机仿真
4.1 影响因素分析
4.2 RSSI定位与RSSID定位误差分析
5. 结束语

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

一种基于接入与回传一体化小基站的用户满意度最大化算法

doi: 10.11999/JEIT171169

通讯作者:
陈前斌 cqb@cqupt.edu.cn

计量

A User Satisfaction Maximization Algorithm Based on Access and Backhaul Integrated Small Base Station

1. 引言

2. 定位原理

2.1 RSSI值求取距离之比

2.2 根据距离之比定位

3. 算法步骤

3.1 数据预处理

3.2 定位算法

4. 计算机仿真

4.1 影响因素分析

4.1.1 接收信噪比SNR对定位精度的影响

4.1.2 监测站间距对定位精度的影响

4.2 RSSI定位与RSSID定位误差分析

4.2.1 数据预处理

4.2.2 单目标定位

4.2.3 多目标定位

5. 结束语

期刊类型引用(12)

其他类型引用(16)

计量

目录

1. 引言

2. 定位原理

2.1 RSSI值求取距离之比

2.2 根据距离之比定位

3. 算法步骤

3.1 数据预处理

3.2 定位算法

4. 计算机仿真

4.1 影响因素分析

4.2 RSSI定位与RSSID定位误差分析

5. 结束语

留言板

一种基于接入与回传一体化小基站的用户满意度最大化算法

doi: 10.11999/JEIT171169

通讯作者: 陈前斌 cqb@cqupt.edu.cn

计量

出版历程

A User Satisfaction Maximization Algorithm Based on Access and Backhaul Integrated Small Base Station

1. 引言

2. 定位原理

2.1 RSSI值求取距离之比

2.2 根据距离之比定位

3. 算法步骤

3.1 数据预处理

3.2 定位算法

4. 计算机仿真

4.1 影响因素分析

4.1.1 接收信噪比SNR对定位精度的影响

4.1.2 监测站间距对定位精度的影响

4.2 RSSI定位与RSSID定位误差分析

4.2.1 数据预处理

4.2.2 单目标定位

4.2.3 多目标定位

5. 结束语

期刊类型引用(12)

其他类型引用(16)

计量

出版历程

目录

1. 引言

2. 定位原理

2.1 RSSI值求取距离之比

2.2 根据距离之比定位

3. 算法步骤

3.1 数据预处理

3.2 定位算法

4. 计算机仿真

4.1 影响因素分析

4.2 RSSI定位与RSSID定位误差分析

5. 结束语

通讯作者:
陈前斌 cqb@cqupt.edu.cn