Adaptive Sensor Scheduling Algorithm for Target Tracking in Wireless Sensor Networks
-
摘要: 在无线传感器网络目标跟踪的过程中进行节点调度,可以综合考虑跟踪误差和能量消耗,延长传感器网络的使用寿命。为了综合考虑节点调度的短期和长远损失,该文将问题建模为部分可观测马尔科夫决策过程(POMDP)以得到更优的调度策略,并提出一种近似求解算法C-QMDP。该算法利用马尔科夫链蒙特卡洛方法(MCMC)推导连续状态空间的置信状态的转移,并计算瞬时代价。使用状态离散化方法,基于马尔科夫决策过程(MDP)值迭代求解未来代价的近似值。仿真结果表明,相比现有POMDP近似算法,该文算法既可以降低跟踪过程中的累积损失,又可以将大量运算进行离线计算,减小了在线决策时的计算量。
-
关键词:
- 无线传感器网络 /
- 目标跟踪 /
- 节点调度 /
- 部分可观测马尔可夫决策过程
Abstract: In the process of target tracking, the sensor scheduling algorithm can achieve the tradeoff between the tracking error and the energy consumption so as to extend the service life of the sensor network. The issue can be modeled as a Partially Observable Markov Decision Process (POMDP), which takes both short- and long- term losses of sensor scheduling into account and makes a better decision. A C-QMDP approximation algorithm suitable for continuous state space is proposed. The Markov Chain Monte Carlo (MCMC) method is used to derive the transfer function of belief state and calculate the instantaneous cost. The state discretization method is used to solve the approximation of future cost based on Markov Decision Process (MDP) iteration. Simulation results show that compared to the existing POMDP approximation algorithms, the proposed algorithm can reduce the cumulative losses and computation load in the tracking process by offline computation. -
表 1 C-QMDP算法
算法 1 C-QMDP算法
输入:置信状态(包括粒子状态和粒子权重):
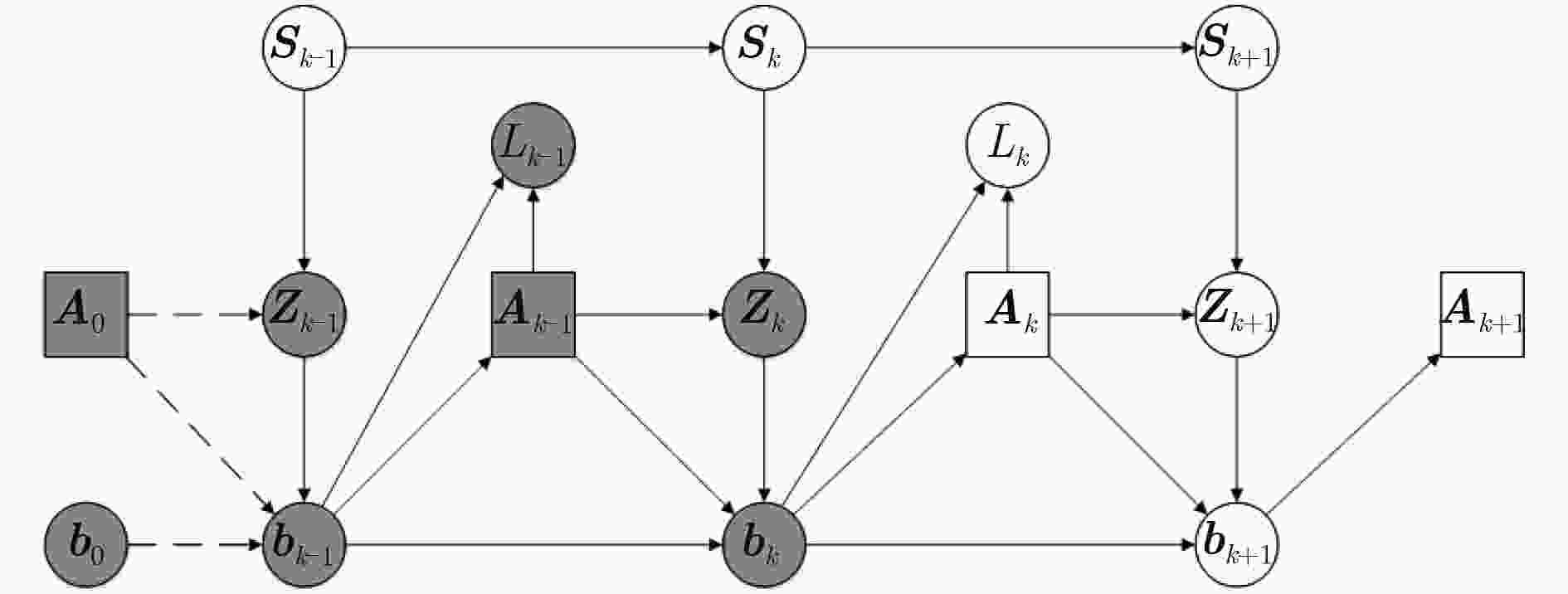
${{{b}}_k} = \left({{S}}_k^{(1)},\tilde w_k^{(1)},{{S}}_k^{(2)},\tilde w_k^{(2)},·\!·\!·,{{S}}_k^{(N)},\tilde w_k^{(N)}\right)$
输出:最优动作A
(1) function C-QMDP( ${{{b}}_k}$)
(2) $V\!\, \raisebox{4pt}{\hat} \leftarrow {\rm{MDP\_discrete\_value\_iteration()}}$
(3) for all control actions A do
(4) ${{{b}}_{k + 1}} \leftarrow {\rm{Particle\_filter(}}{{{b}}_k},{{A}}{\rm{)}}$
(5) for i = 1 : N do
(6) ${\tilde{ S}}_{k + 1}^{(i)} \leftarrow {{S}}_{k + 1}^{(i)}$
(7) end for
(8) $Q({{{b}}_k},{{A}}) = L({{{b}}_k},{{A}}) + \beta \sum\limits_{i = 1}^N {\tilde w_k^{(i)}V\!\, \raisebox{4pt}{\hat}\left({\tilde{ S}}_{k + 1}^{(i)}\right)} $
(9) end for
(10) return $\arg \mathop {\max }\limits_{{A}} Q({{{b}}_k},{{A}})$
(11) end function表 2 C-QMDP与其余算法性能比较
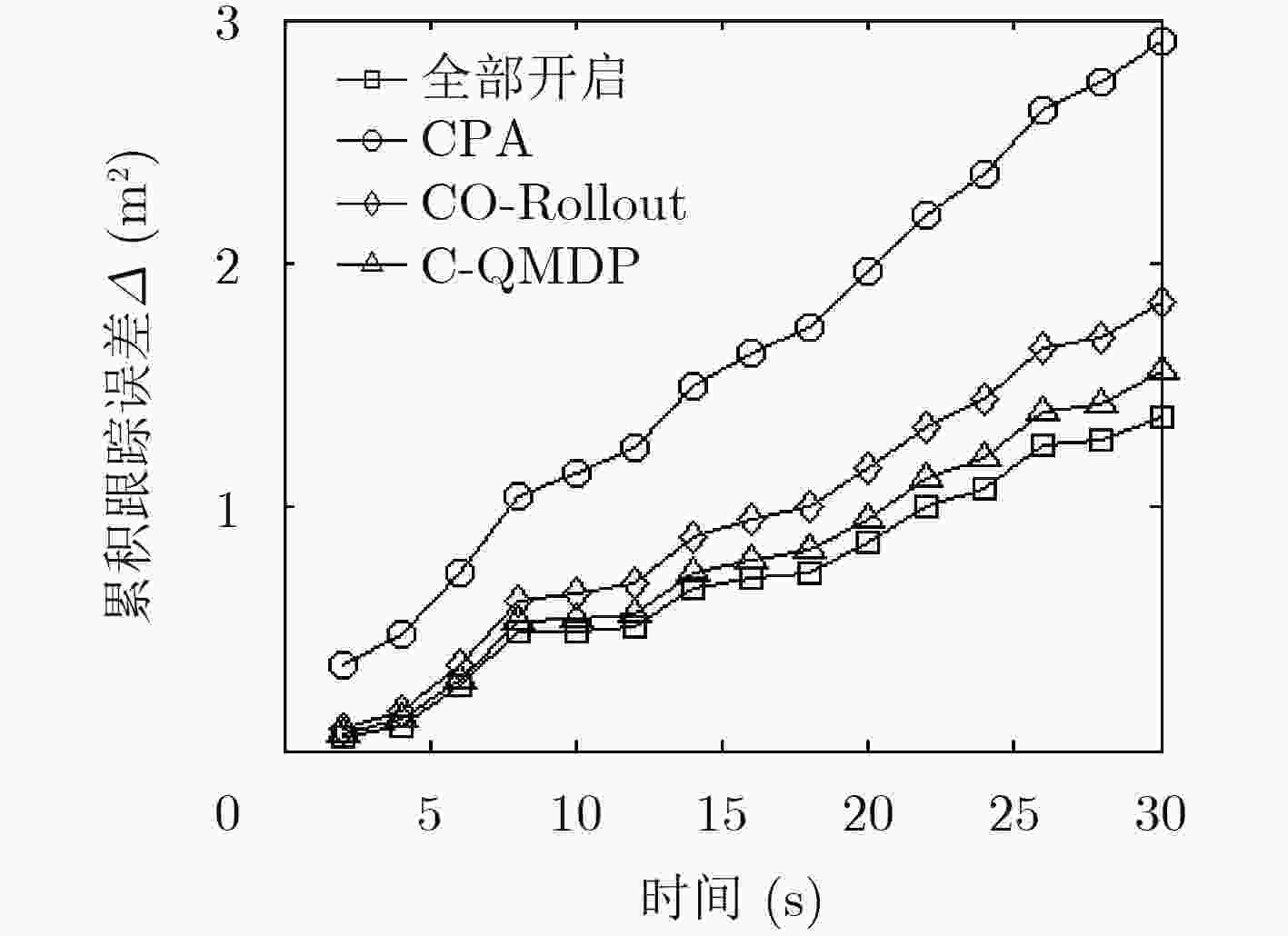
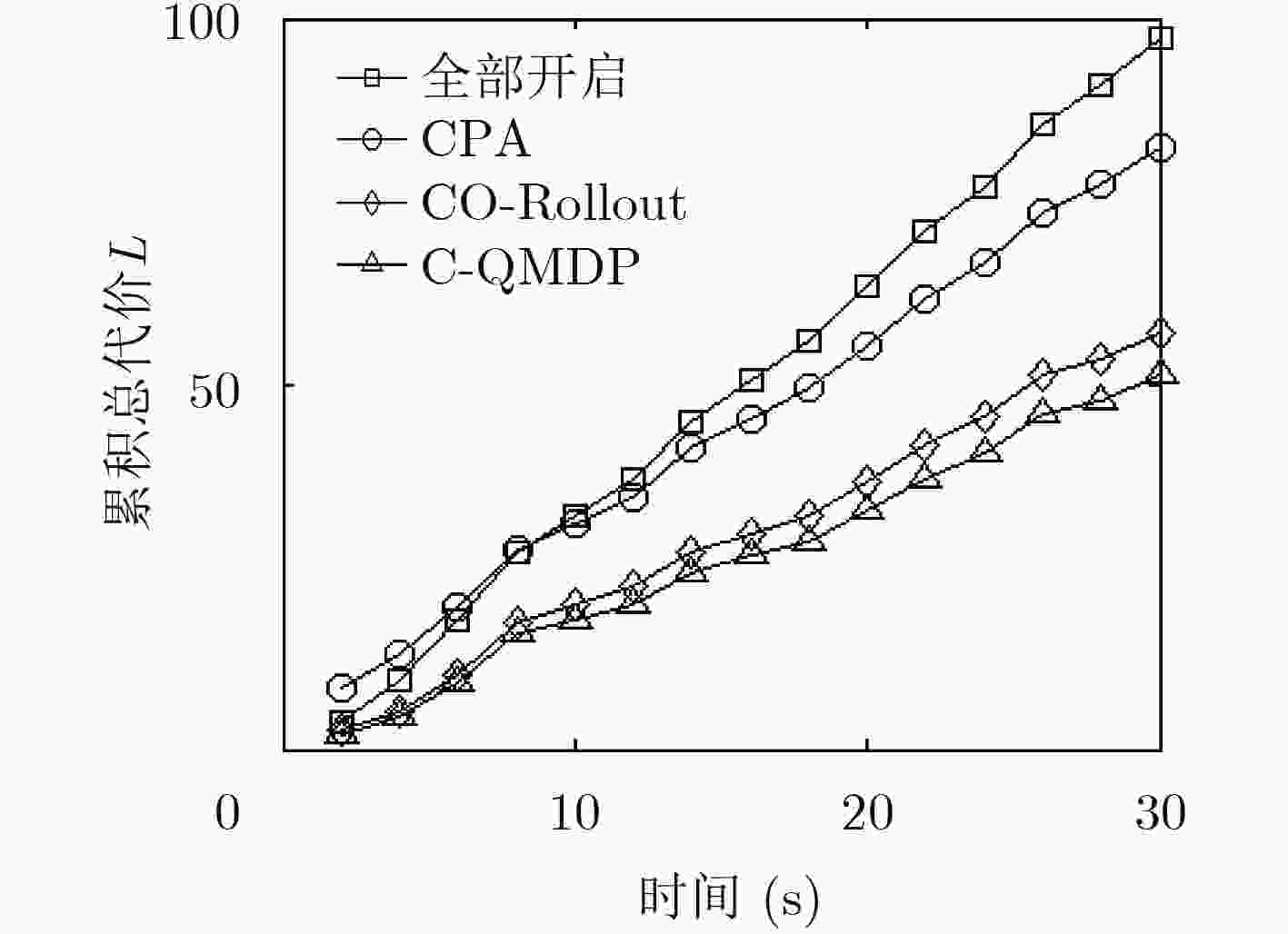
算法 跟踪误差 传感器功耗 总代价 全部开启 1.3647 70.0722 97.3662 CPA 2.9132 24.0217 82.2857 CO-Rollout 1.8371 20.3493 57.0913 C-QMDP 1.5542 20.0906 51.1746 -
ALCALA J M, URENA J U, HERNANDEZ A, et al. Sustainable homecare monitoring system by sensing electricity data[J]. IEEE Sensors Journal, 2017, 17(23): 7741–7749 doi: 10.1109/JSEN.2017.2713645 MARTELLI T, BONGIOANNI C, COLONE F, et al. Security enhancement in small private airports through active and passive radar sensors[C]. 17th IEEE International Conference on Radar Symposium (IRS), Krakow, Poland, 2016: 1–5. SHI W Y and CHIAO J C. Neural network based real-time heart sound monitor using a wireless wearable wrist sensor[C]. IEEE Conference on Circuits and Systems Conference (DCAS), Arlington, USA, 2016: 1–4. ANGLEY D, SUVOROVA S, RISTIC B, et al. Sensor scheduling for target tracking in large multistatic sonobuoy fields[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Arlington, USA, 2017: 3146–3150. SONG R, WEI Q, and XIAO W. ADP-based optimal sensor scheduling for target tracking in energy harvesting wireless sensor networks[J]. Neural Computing and Applications, 2016, 27(6): 1543–1551 doi: 10.1007/s00521-015-1954-4 YANG X, ZHANG W A, CHEN M Z Q, et al. Hybrid sequential fusion estimation for asynchronous sensor network-based target tracking[J]. IEEE Transactions on Control Systems Technology, 2017, 25(2): 669–676 doi: 10.1109/TCST.2016.2558632 唐显锭, 冯辉, 杨涛, 等. 无线传感器网络中用于目标跟踪的节点规划算法[J]. 太赫兹科学与电子信息学报, 2014, 12(3): 355–361 doi: 10.11805/TKYDA201403.0355TANG Xianding, FENG Hui, YANG Tao, et al. Sensor scheduling for target tracking in wireless sensor networks[J]. Journal of Terahertz Science and Electronic Information Technology, 2014, 12(3): 355–361 doi: 10.11805/TKYDA201403.0355 ZHANG H, AYOUB R, and SUNDARAM S. Sensor selection for Kalman filtering of linear dynamical systems: Complexity, limitations and greedy algorithms[J]. Automatica, 2017, 78: 202–210 doi: 10.1016/j.automatica.2016.12.025 冉晓旻, 方德亮. 基于势博弈的分布式目标跟踪传感器分配算法[J]. 电子与信息学报, 2017, 39(11): 2748–2754 doi: 10.11999/JEIT170229RAN Xiaomin and FANG Deliang. Distributed sensor allocation algorithm for target tracking based on potential game[J]. Journal of Electronics&Information Technology, 2017, 39(11): 2748–2754 doi: 10.11999/JEIT170229 SINGH P, CHEN M, CARLONE L, et al. Supermodular mean squared error minimization for sensor scheduling in optimal Kalman filtering[C]. IEEE Conference on American Control Conference (ACC), Seattle, USA, 2017: 5787–5794. ASGHAR A B, JAWAID S T, and SMITH S L. A complete greedy algorithm for infinite-horizon sensor scheduling[J]. Automatica, 2017, 81: 335–341 doi: 10.1016/j.automatica.2017.04.018 SPAAN M T J. Partially Observable Markov Decision Processes[M]. Berlin Heidelberg: Springer, 2012: 387–414. ZOIS D S, LEVORATO M, and MITRA U. Active classification for POMDPs: A Kalman-like state estimator[J]. IEEE Transactions on Signal Processing, 2014, 62(23): 6209–6224 doi: 10.1109/TSP.2014.2362098 ZOIS D S and MITRA U. Active state tracking with sensing costs: Analysis of two-states and methods for n-states[J]. IEEE Transactions on Signal Processing, 2017, 65(11): 2828–2843 doi: 10.1109/TSP.2017.2664049 SHANI G, PINEAU J, and KAPLOW R. A survey of point-based POMDP solvers[J]. Autonomous Agents and Multi-Agent Systems, 2013, 27(1): 1–51 doi: 10.1007/s10458-012-9200-2 LITTMAN M L, CASSANDRA A R, and KAELBLING L P. Learning policies for partially observable environments: Scaling up[C]. Proceedings of the 12th International Conference on Machine Learning, Tahoe City, USA, 1995: 362–370. RUSSELL S. Artificial Intelligence: A Modern Approach. Making Complex Decisions (Ch-17)[M]. Englewood Cliffs: Prentice-Hall, 2004: 645–692. HE Y and CHONG K P. Sensor scheduling for target tracking in sensor networks[C]. 43rd IEEE Conference on Decision and Control(CDC), Nassau, Bahamas, 2004: 743–748. CHONG E K P, KREUCHER C M, and HERO III A O. POMDP Approximation Using Simulation and Heuristics[M]. Boston, MA: Springer, 2008: 95–119. LI Y, KRAKOW L W, CHONG E K P, et al. Dynamic sensor management for multisensor multitarget tracking[C]. IEEE 40th Annual Conference on Information Sciences and Systems, Princeton, USA, 2006: 1397–1402. LI Y, KRAKOW L W, CHONG E K P, et al. Approximate stochastic dynamic programming for sensor scheduling to track multiple targets[J]. Digital Signal Processing, 2009, 19(6): 978–989 doi: 10.1016/j.dsp.2007.05.004 BAR-SHALOM Y, LI X R, and KIRUBARAJAN T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software[M]. New York: John Wiley & Sons, 2004: 199–266. ALIPPI C and VANINI G. A RSSI-based and calibrated centralized localization technique for Wireless Sensor Networks[C]. Fourth Annual IEEE International Conference on Pervasive Computing and Communications Workshops, Pisa, Italy, 2006: 301–305. NIU R and VARSHNEY P K. Target location estimation in sensor networks with quantized data[J]. IEEE Transactions on Signal Processing, 2006, 54(12): 4519–4528 doi: 10.1109/TSP.2006.882082 ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174–188 doi: 10.1109/78.978374 RUSSELL S. Artificial Intelligence: A Modern Approach. Probabilistic Reasoning Over Time (Ch-15)[M]. Englewood Cliffs: Prentice-Hall, 2004: 566–609. HE Y and CHONG E K P. Sensor scheduling for target tracking: A Monte Carlo sampling approach[J]. Digital Signal Processing, 2006, 16(5): 533–545 doi: 10.1016/j.dsp.2005.02.005 -





 下载:
下载:
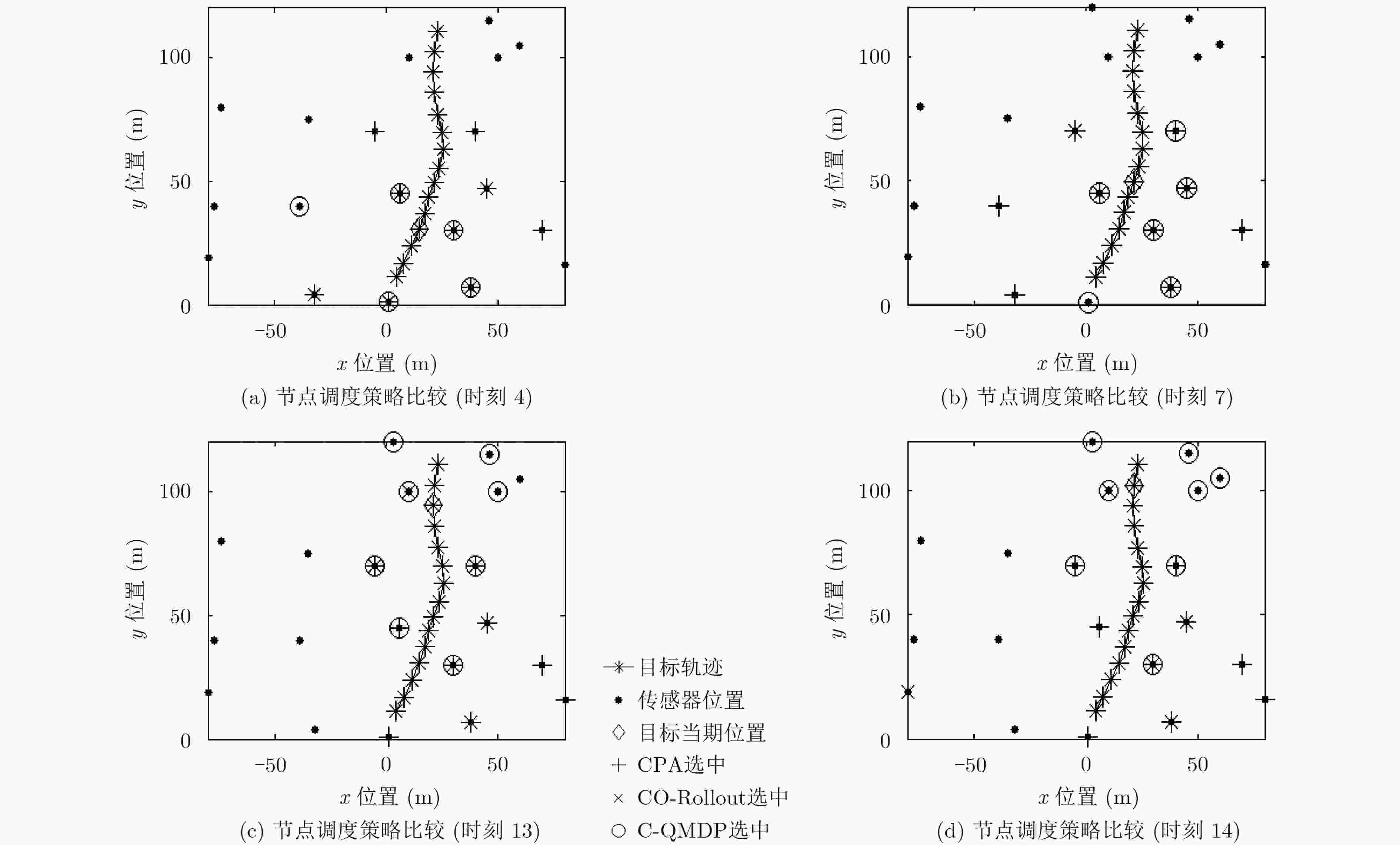


 下载:
下载:
