Frequency Locator Polynomial Based Fast Algorithm for Sparse Aliased Spectrum Recovery
-
摘要: 论文提出一种基于频率位置多项式的稀疏混叠频谱快速恢复算法。该算法使用不同延时的多通道欠采样得到的信号混叠频谱,通过建立频率位置多项式,快速定位非零频点,并有效地将非线性的频谱恢复问题转换成一系列线性方程组的求解问题。该算法的计算速度相对国外同类算法(BigBand)有显著提高,并且实验结果表明该算法具有更低的频谱恢复错误率。Abstract: A fast algorithm based on Frequency Locator Polynomial (FLP) for sparse spectrum recovery is proposed. Using the shifted subsampled signals, the FLPs are constructed, thus to locate rapidly the nonzero frequencies. In particular, the nonlinear problem of sparse spectrum recovery is converted into solving a series of linear equations. Experimental results show that the proposed algorithm exhibits higher processing speed and lower error spectrum reconstruction rate than its predecessor BigBand.
-
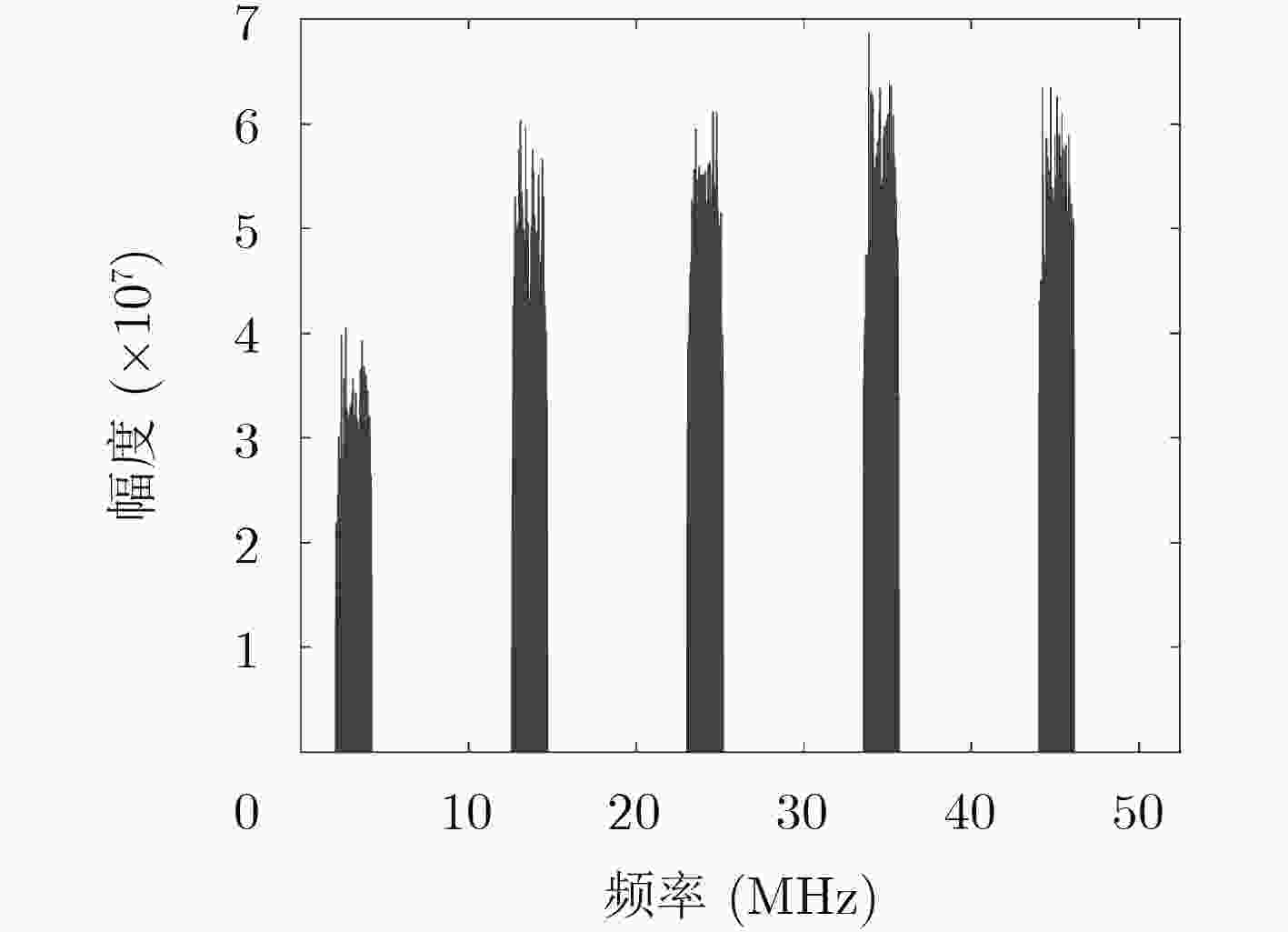
图 3 文献[9]恢复的频谱
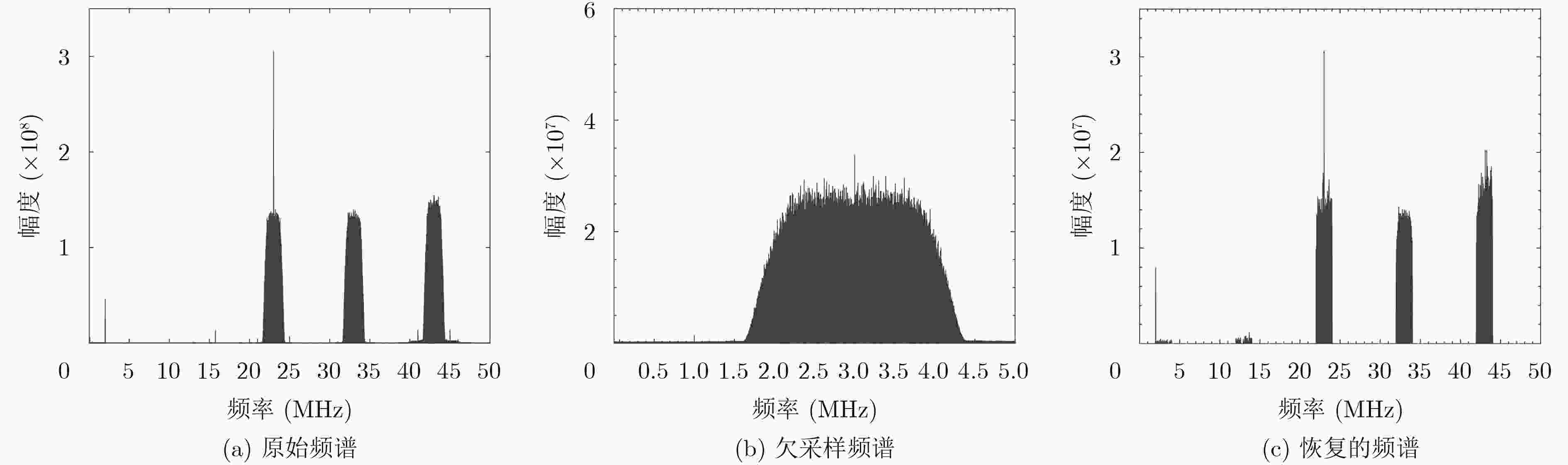
表 1 原始频谱中的信号
信号 调制类型 载频(MHz) 波特率(MHz) A QPSK 23 2 B QPSK 33 2 C QPSK 43 2 -
MISHALI M. Sub-Nyquist sampling[J]. IEEE Signal Processing Magazine, 2011, 28(6): 98–124 doi: 10.1109/MSP.2011.942308 COHEN D, TSIPER S, and ELDAR Y C. Analog-to-digital cognitive radio: Sampling, detection, and hardware[J]. IEEE Signal Processing Magazine, 2018, 35(1): 137–166 doi: 10.1109/MSP.2017.2740966 JIA Min, SHI Yao, GU Xuemai, et al. Improved algorithm based on modulated wideband converter for multiband signal reconstruction[J]. EURASIP Journal on Wireless Communications and Networking, 2016(1): 1–9 doi: 10.1186/s13638-016-0547-y JAGANATHAN K, ELDAR Y C, and HASSIBI B. Sparse phase retrieval: Uniqueness guarantees and recovery algorithms[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 65(9): 2402–2410 doi: 10.1109/TSP.2017.2656844 QIN Zhijin, GAO Yue, PLUMBLEY M D, et al. Wideband spectrum sensing on real-time signals at sub-Nyquist sampling rates in single and cooperative multiple nodes[J]. IEEE Transactions on Signal Processing, 2016, 64(12): 3106–3117 doi: 10.1109/TSP.2015.2512562 LOPEZ-PARRADO A and VELASCO-MEDINA J. Cooperative wideband spectrum sensing based on sub-Nyquist sparse fast Fourier transform[J]. IEEE Transactions on Circuits&Systems II Express Briefs, 2015, 63(1): 39–43 doi: 10.1109/TCSII.2015.2483278 QIN Si, ZHANG Yimin D, AMIN M G, et al. Generalized coprime sampling of Toeplitz matrix for spectrum estimation[J]. IEEE Transactions on Signal Processing, 2017, 65(1): 81–94 doi: 10.1109/TSP.2016.2614799 ZENG Weijun, WANG Huali, and TIAN Hui. Multirate coprime sampling of sparse multiband signals[J]. IEICE Transactions on Fundamentals of Electronics Communications&Computer Sciences, 2016, E99.A(4): 839–842 doi: 10.1587/transfun.E99.A.839 HASSANIEH H, SHI Lixin, ABARI O, et al. GHz-wide sensing and decoding using the sparse Fourier transform[C]. IEEE International Conference on Computer Communications, Toronto, Canada, 2014: 2256–2264. ALBDROUBI A and GROCHENIG K. Nonuniform sampling and reconstruction in shift-invariant spaces[J]. SIAM Review, 2001, 43(4): 585–620 doi: 10.1137/S0036144501386986 DONG Ningfei, WANG Jianxin, and YU Hai. Discrete blind reconstruction method for multi-coset sampling[J]. IET Signal Processing, 2016, 10(5): 465–470 doi: 10.1049/iet-spr.2015.0391 FENG Guiliang and TZENG K K. A generalization of the Berlekamp-Massey algorithm for multisequence shift-register synthesis with applications to decoding cyclic codes[J]. IEEE Transactions on Information Theory, 1991, 37(5): 1274–1287 doi: 10.1109/18.133246 SAHOO S K and MAKUR A. Signal recovery from random measurements via extended orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2015, 63(10): 2572–2581 doi: 10.1109/TSP.2015.2413384 -





 下载:
下载:


 下载:
下载:
