A One-dimensional Discrete Map Chaos Criterion Theorem with Applications in Pseudo-random Number Generator
-
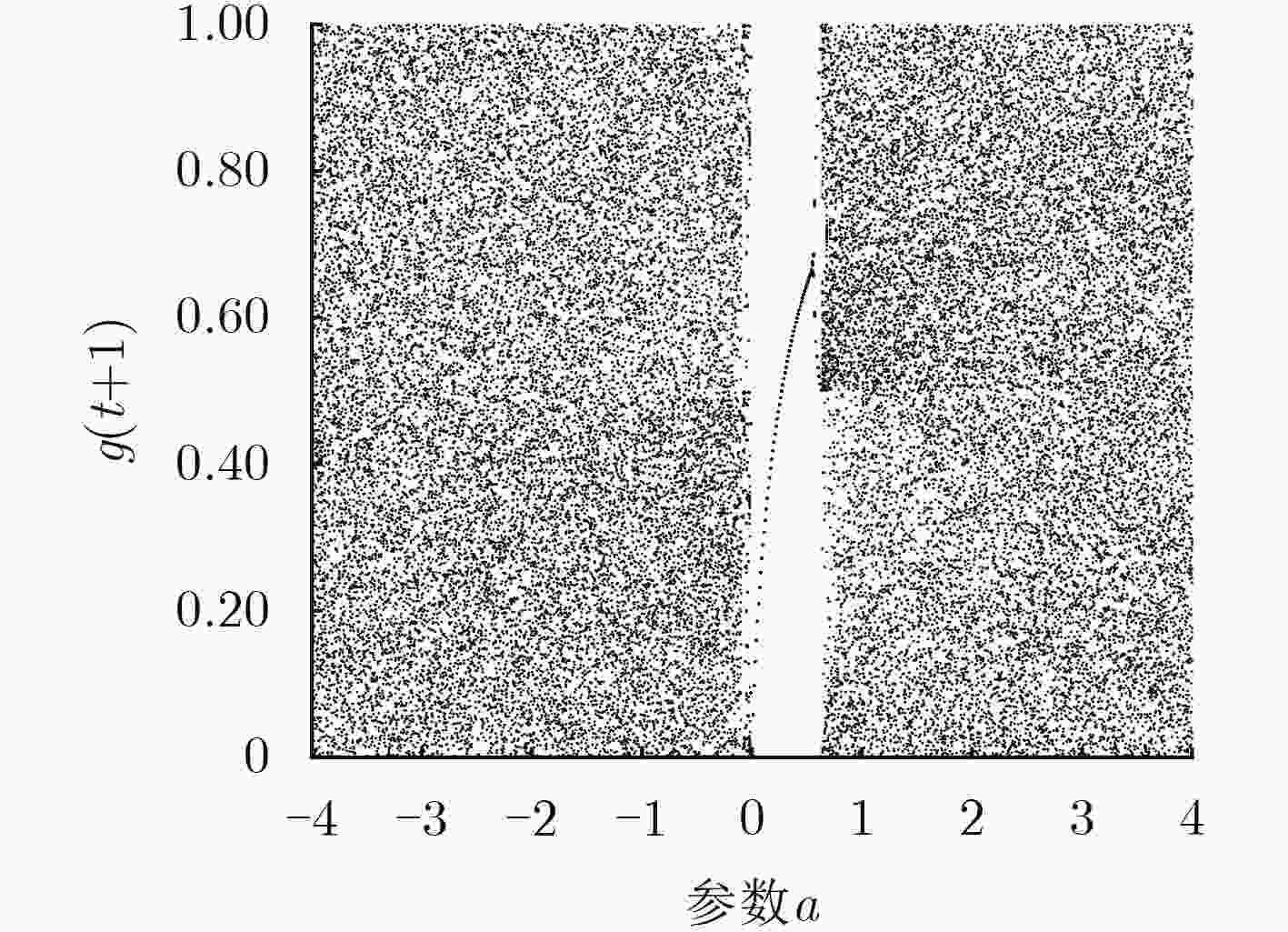
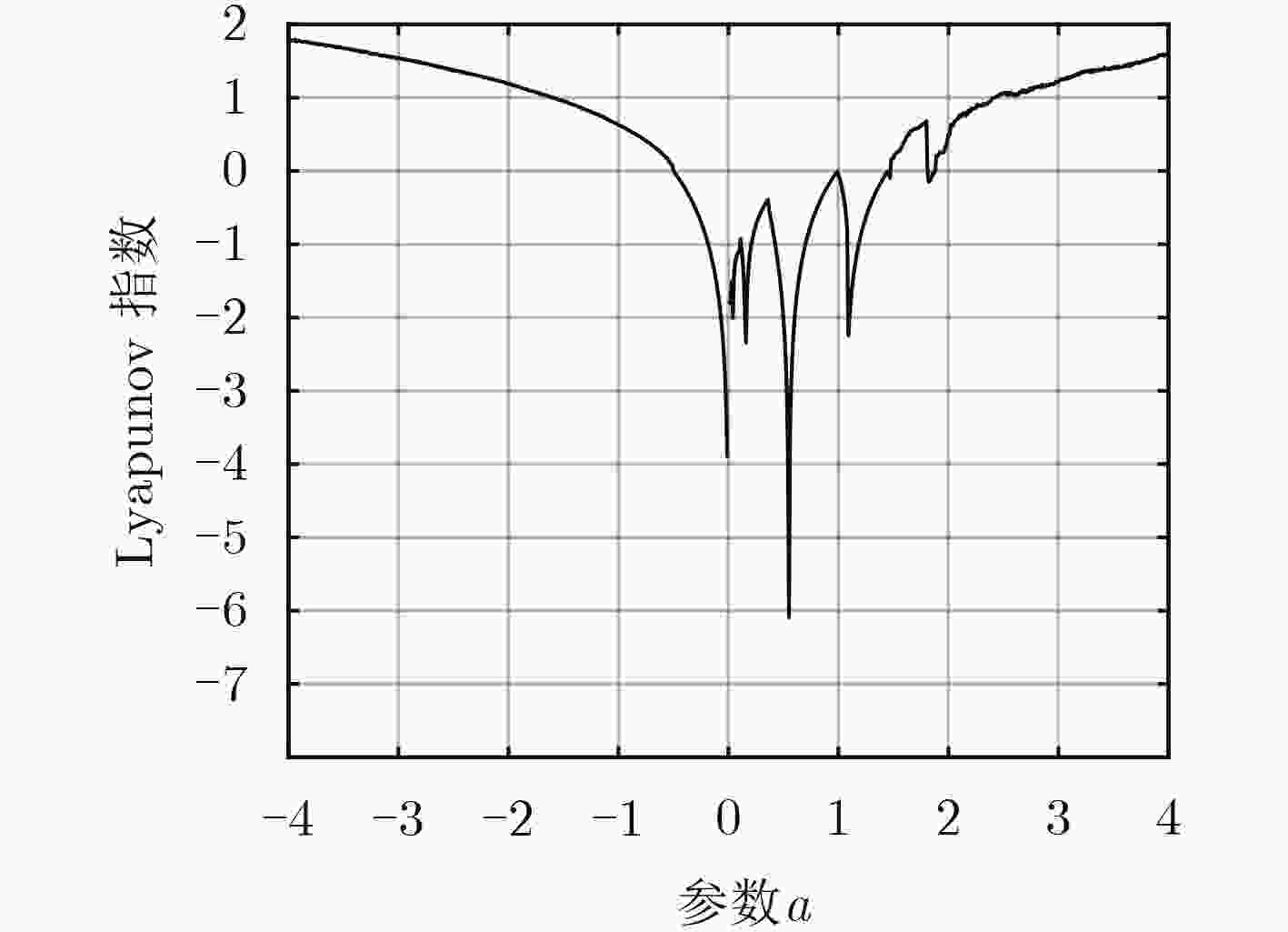
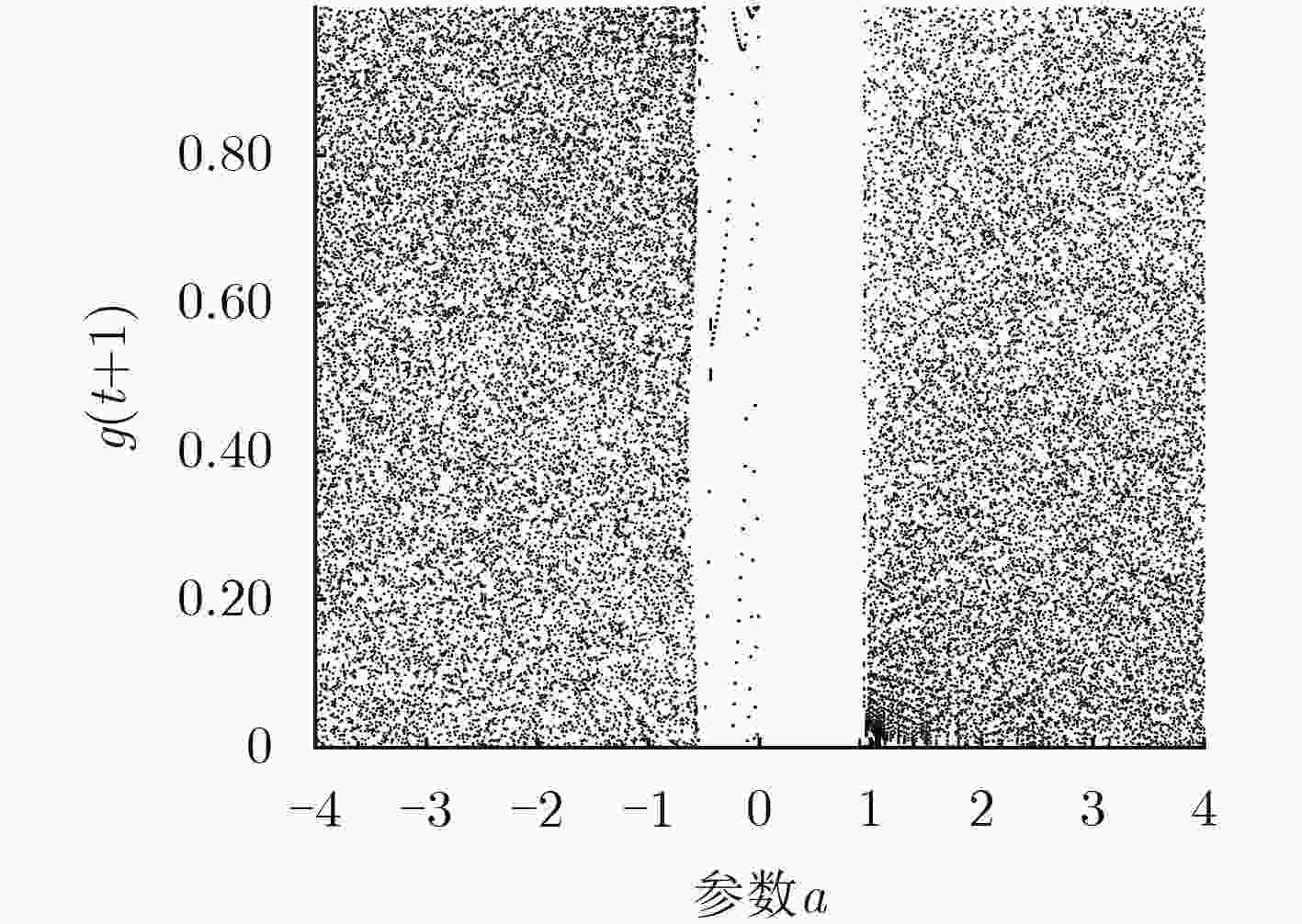
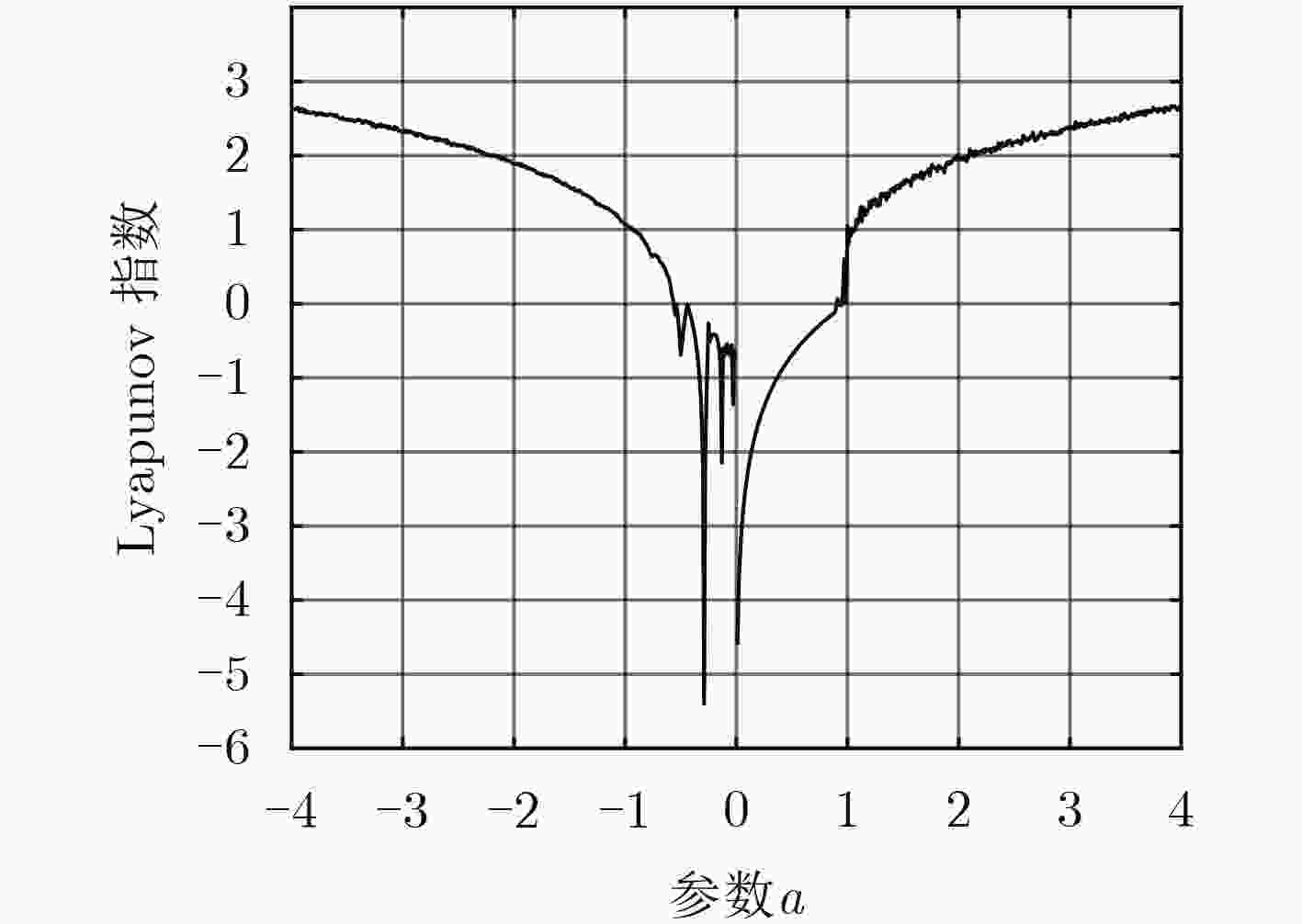
摘要: 该文研究了一类取模运算的1维离散动力系统,提出了一个这类离散映射的混沌判据,利用Marotto定理证明了其混沌的存在性。给出了几个满足该判据的特殊形式的系统,分析了其分岔图、Lyapunov指数谱等基本动力学性质,通过模拟结果验证了理论的正确性。基于新系统设计了一个伪随机数发生器(PRNG), SP800-22随机性检测结果表明了该序列具有良好的伪随机性。进一步给出了一个图像加密方案,其密钥空间可以达到2747。该文提出的新系统的系统参数可以无穷多,所以理论上该加密方案的密钥空间可以无穷大。Abstract: A novel one-dimensional discrete chaotic criterion is firstly constructed by studying the modular operation of the discrete dynamical systems. The judgement of the Marotto theorem is used to prove that the suggested dynamical systems are chaotic. Secondly, several special chaotic systems satisfied with the conditions of this paper are given, and the bifurcation diagram and Lyapunov exponential spectrum are also analyzed. Numerical simulations show that the proposed chaotic systems have the positive Lyapunov exponent, which indicates the accuracy of the proposed theory. Additionally, a Pseudo-Random Number Generator (PRNG) is also designed based on the given new chaotic system. Using SP800-22 test suit, the results show that the output sequence of PRNG has good pseudorandom. Finally, as an application of the PRNG, an image encryption algorithm is given. The proposed encryption scheme is highly secure Key space of 2747 and can resist against the statistical and exhaustive attacks based on the experimental results.
-
表 1 SP800-22随机性检验结果
检测项目 给定初始值 参数扰动100次 P-值 检测结果 拟合优度P-值 通过率 频率测试 0.1493 通过 0.8978 0.97 块内频率测试 0.6436 通过 0.3041 0.99 向前累积和测试 0.2777 通过 0.3191 0.97 向后累积和测试 0.1971 通过 0.8832 0.98 游程测试 0.3875 通过 0.1453 0.97 块内最长连续1测试 0.5564 通过 0.4559 1.00 二元矩阵秩测试 0.0523 通过 0.9463 1.00 离散傅里叶变换测试 0.1445 通过 0.4373 0.99 非重叠模板匹配测试 0.5761 通过 0.7598 0.99 重叠模板匹配测试 0.2961 通过 0.1719 0.98 全局通用统计测试 0.2253 通过 0.9963 0.99 近似熵检测 0.5118 通过 0.6579 1.00 随机偏移测试 0.0246 通过 0.7598 1.00 随机偏移变量测试 0.5542 通过 0.0072 0.98 线性复杂度测试 0.4339 通过 0.2023 0.99 串行测试 0.9780 通过 0.4190 0.98 -
LI T Y and YORKE J A. Period three implies chaos[J]. American Mathematical Monthly, 1975, 82(10): 985–992. DOI: 10.2307/2318254. YU Xingmei, MIN Lequan, and CHEN Tianyu. Chaos criterion on some quadric polynomial maps and design for chaotic pseudorandom number generator[C]. Seventh International Conference on Natural Computation, Shanghai, 2011: 1373–1376. 周海玲, 宋恩彬. 二次多项式映射的3-周期点判定[J]. 四川大学学报(自然科学版), 2009, 46(3): 561–564. DOI: 103969/j.issn.0490-6756.2009.03-009.ZHOU Hailing and SONG Enbin. Discrimination of the 3-periodic points of a quadratic polynomial[J]. Journal of Sichuan University(Natural Science Edition), 2009, 46(3): 561–564. DOI: 103969/j.issn.0490-6756.2009.03-009. YANG Xiuping, MIN Lequan, and WANG Xue. A cubic map chaos criterion theorem with applications in generalized synchronization based pseudorandom number generator and image encryption[J]. Chaos, 2015, 25(5): 053104. DOI: 10.1063/1.4917380. MAROTTO F R. Snap-back repellers imply chaos in Rn[J]. Journal of Mathematical Analysis & Applications, 1978, 63(1): 199–223. DOI: 10.1016/0022-247X(78)90115-4. CHEN Guangrong and LAI Dejian. Feedback control of lyapunov exponents for discrete-time dynamical systems[J]. International Journal of Bifurcation & Chaos, 1996, 6(7): 1341–1349. DOI: 10.1142/S021812749600076X. HAN Dandan, MIN Lequan, and CHEN Guangrong. A stream encryption scheme with both key and plaintext avalanche effects for designing chaos-based pseudorandom number generator with application to image encryption[J]. International Journal Bifurcation & Chaos, 2016, 26(5): 1650091-1. DOI: 10.1142/S0218127416500917. 韩丹丹, 闵乐泉, 赵耿. 八维广义同步系统在伪随机数发生器中的应用[J]. 电子与信息学报, 2016, 38(5): 1158–1165. DOI: 10.11999/JEIT150899.HAN Dandan, MIN Lequan, and ZHAO Geng. Application of 8-dimensional generalized synchronization system in pseudorandom number generator[J]. Journal of Electronics & Information Technology, 2016, 38(5): 1158–1165. DOI: 10.11999/JEIT150899. RUKHIN A, SOTO J, NECHVATAL J, et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications[R]. National Institute of Standards and Technology Special Publication, 2010. LI Pei, MIN Lequan, ZANG Hongyan, et al. A generalized chaos synchronization-based pseudo-random generator number and performance analysis[C]. International Conference on Communications Circuits and Systems, Chengdu, China, 2010: 781–785. WANG Xingyuan, LIU Chuanming, XU Dahai, et al.. Image encryption scheme using chaos and simulated annealing algorithm[J]. Nonlinear Dynamics, 2016, 84(3): 1417–1429. DOI: 10.1007/s11071-015-2579-y. LI Yueping, WANG Chunhua, and CHEN Hua. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation[J]. Optics & Lasers in Engineering, 2017, 90: 238–246. DOI: 10.1016/j.optlaseng.2016.10.020. WANG Xingyuan, LIU Chuanming, and ZHANG Huili. An effective and fast image encryption algorithm based on chaos and interweaving of ranks[J]. Nonlinear Dynamics, 2016, 84(3): 1595–1607. DOI: 10.1007/s11071-015-2590-3. GUESMI R, FARAH M A B, KACHOURI A, et al.. A novel chaos-based image encryption using DNA sequence operation and secure hash algorithm SHA-2[J]. Nonlinear Dynamics, 2016, 83(3): 1123–1136. DOI: 10.1007/s11071-015-2392-7. BELAZI A, EL-LATIF A A A, DIACONU A V, et al.. Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms[J]. Optics & Lasers in Engineering, 2017, 88: 37–50. DOI: 10.1016/j.optlaseng.2016.07.010. -





 下载:
下载:



 下载:
下载:
