Multi-model Real-time Compressive Tracking
-
摘要: 目标跟踪易受光照、遮挡、尺度、背景及快速运动等因素的影响,还要求较高的实时性。目标跟踪中基于压缩感知的跟踪算法实时性好,但目标外观变化较大时跟踪效果不理想。该文基于压缩感知的框架提出多模型的实时压缩跟踪算法(MMCT),采用压缩感知来降低跟踪过程产生的高维特征,保证实时性能;通过判断前两帧的分类器最大分类分数的差值来选择最合适的模型,提高了定位的准确性;提出新的模型更新策略,按照决策分类器的不同采用固定或动态的学习率,提高了分类精度。MMCT引入的多模型没有增加计算负担,表现出优异的实时性能。实验结果表明,MMCT算法能够很好地适应光照、遮挡、复杂背景及平面旋转的情况。Abstract: Object tracking is easily influenced by illumination, occlusion, scale, background clutter, and fast motion, and it requires higher real-time performance. The object tracking algorithm based on compressive sensing has a better real-time performance but performs weakly in tracking when object appearance is changed greatly. Based on the framework of compressive sensing, a Multi-Model real-time Compressive Tracking (MMCT) algorithm is proposed, which adopts the compressive sensing to decrease the high dimensional features for the tracking process and to satisfy the real-time performance. The MMCT algorithm selects the most suitable classifier by judging the maximum classification score difference of classifiers in the previous two frames, and enhances the accuracy of location. The MMCT algorithm also presents a new model update strategy, which employs the fixed or dynamic learning rates according to the differences of decision classifiers and improves the precision of classification. The multi-model introduced by MMCT does not increase the computational burden and shows an excellent real-time performance. The experimental results indicate that the MMCT algorithm can well adapt to illumination, occlusion, background clutter and plane-rotation.
-
Key words:
- Object tracking /
- Compressive Sensing (CS) /
- Real-time /
- Multi-model /
- Dynamic learning rate
-
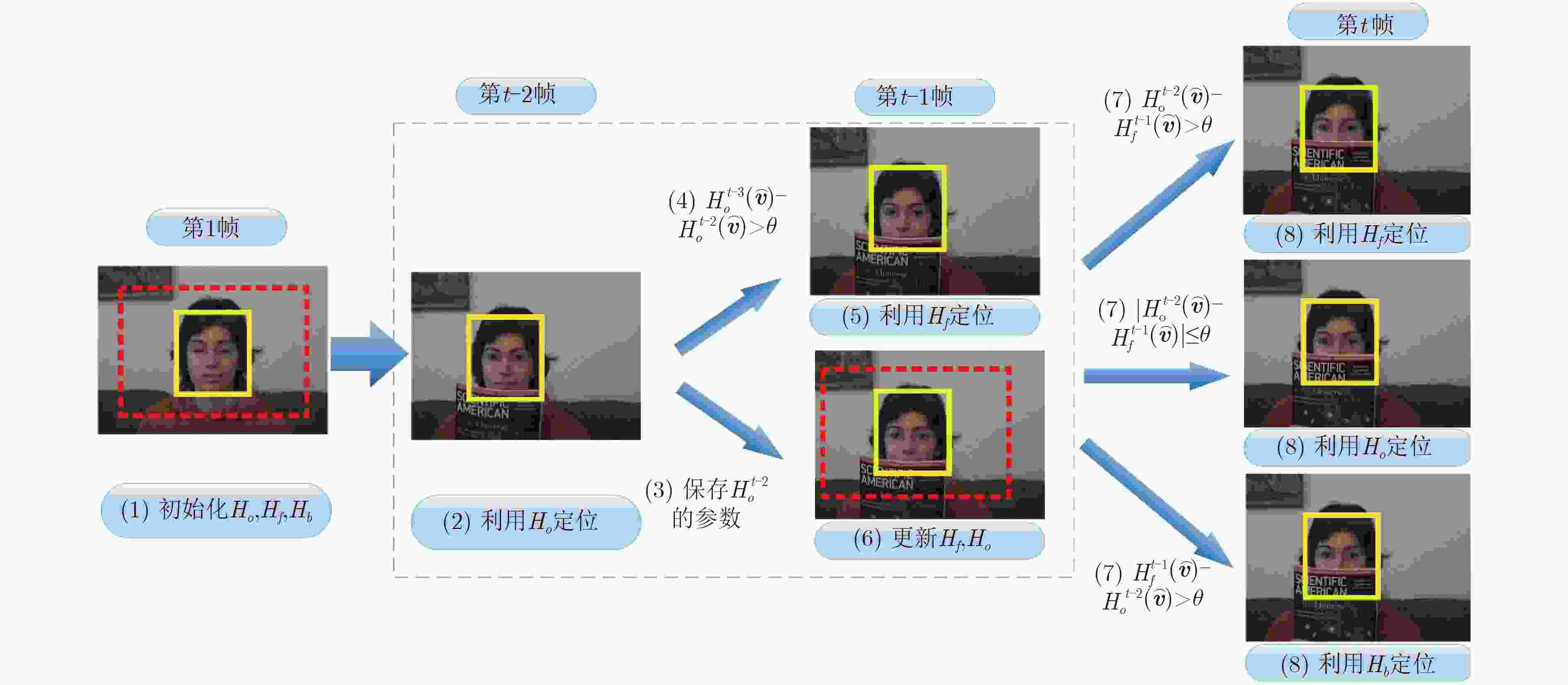
表 1 基于多模型的实时压缩跟踪算法
输入:第t帧的图像 输出:第t帧的目标位置 (1) if $H_*^{t - 2}(\overset{\frown}{{{v}}} ) - H_*^{t - 1}(\overset{\frown}{{{v}}} ) > \theta $ && flag=0 (2) 利用 ${H_f}$及参数 $\{ \mu _f^1,\sigma _f^1,\mu _f^0,\sigma _f^0\} $进行定位 $L_t^{} = {\rm{Loc}}({H_f}(\overset{\frown}{{{v}}} ))$,初始 化学习率 ${\lambda _f}$; (3) 采集正、负样本,利用 ${\lambda _o}$更新 ${H_f}$分类器, ${\lambda _f}$更新 ${H_o}$分类器; (4) 设置flag=1,转入第(16)步处理第 $t + 1$帧; (5) end if (6) if $H_*^{t - 1}(\overset{\frown}{{{v}}} ) - H_*^{t - 2}(\overset{\frown}{{{v}}} ) > \theta $ && flag=0 (7) 利用 ${H_b}$及参数 $\{ \mu _b^1,\sigma _b^1,\mu _b^0,\sigma _b^0\} $进行定位 $L_t^{} = {\rm{Loc}}({H_b}(\overset{\frown}{{{v}}} ))$,初始 化学习率 ${\lambda _{b}}$; (8) 采集正、负样本,利用 ${\lambda _o}$更新 ${H_b}$分类器, ${\lambda _{b}}$更新 ${H_o}$分类器; (9) 设置flag=1,转入第(16)步处理第(t+1)帧; (10) end if (11) if$\left| {H_*^{t - 2}(\overset{\frown}{{{v}}} ) - H_*^{t - 1}(\overset{\frown}{{{v}}} )} \right| \le \theta $ && flag=0 (12) 将 ${H_o}$参数保存至 ${H_f}$及 ${H_b}$; (13) 在第 $t$帧确定目标的位置为 $L_t^{} = {\rm{Loc}}({H_o}(\overset{\frown}{{{v}}} ))$,使用学习率 ${\lambda _o}$按照式(4)更新 ${H_o}$分类器; (14) 转入第(1)步处理第 $t + 1$帧; (15) end if (16) if $H_*^{t - 2}(\overset{\frown}{{{v}}} ) - H_*^{t - 1}(\overset{\frown}{{{v}}} ) > \theta $ && flag=1 (17) 利用 ${H_f}$及 $\{ \mu _f^1,\sigma _f^1,\mu _f^0,\sigma _f^0\} $定位 $L_t^{} = {\rm{Loc}}({H_f}(\overset{\frown}{{{v}}} ))$; (18) 采集正、负样本,利用 ${\lambda _o}$更新 ${H_f}$分类器; (19) 按照式(10)更新学习率 ${\lambda _f}$,使用学习率 ${\lambda _f}$更新 ${H_o}$分类器; (20) 转入第(16)步处理第 $t + 1$帧; (21) end if (22) if $H_*^{t - 1}(\overset{\frown}{{{v}}} ) - H_*^{t - 2}(\overset{\frown}{{{v}}} ) > \theta $ && flag=1 (23) 利用 ${H_b}$及 ${\rm{\{ }}\mu _b^1,\sigma _b^1,\mu _b^0,\sigma _b^0{\rm{\} }}$定位 $L_t^{} = {\rm{Loc}}({H_b}(\overset{\frown}{{{v}}} ))$; (24) 采集正、负样本,利用 ${\lambda _o}$更新 ${H_b}$分类器; (25) 按照式(10)更新学习率 $\lambda_b $,使用学习率 ${\lambda _{b}}$更新 ${H_o}$分类器; (26) 转入第(16)步处理第 $t + 1$帧; (27) end if (28) if $\left| {H_*^{t - 1}(\overset{\frown}{{{v}}} ) - H_*^{t - 2}(\overset{\frown}{{{v}}} )} \right| \le \theta $ && flag=1 (29) 将 ${H_o}$参数保存至 ${H_f}$及 ${H_b}$; (30) 确定目标位置为 $L_t^{} = {\rm{Loc}}({H_o}(\overset{\frown}{{{v}}} ))$,利用学习率 ${\lambda _o}$按照式 (4)更新 ${H_o}$分类器; (31) 设置学习率 ${\lambda _f} = 0$和 ${\lambda _{b}} = {\lambda _o}$,将flag设置为0,转到第(1)步 处理第 $t + 1$帧; (32) end if 表 2 跟踪成功率
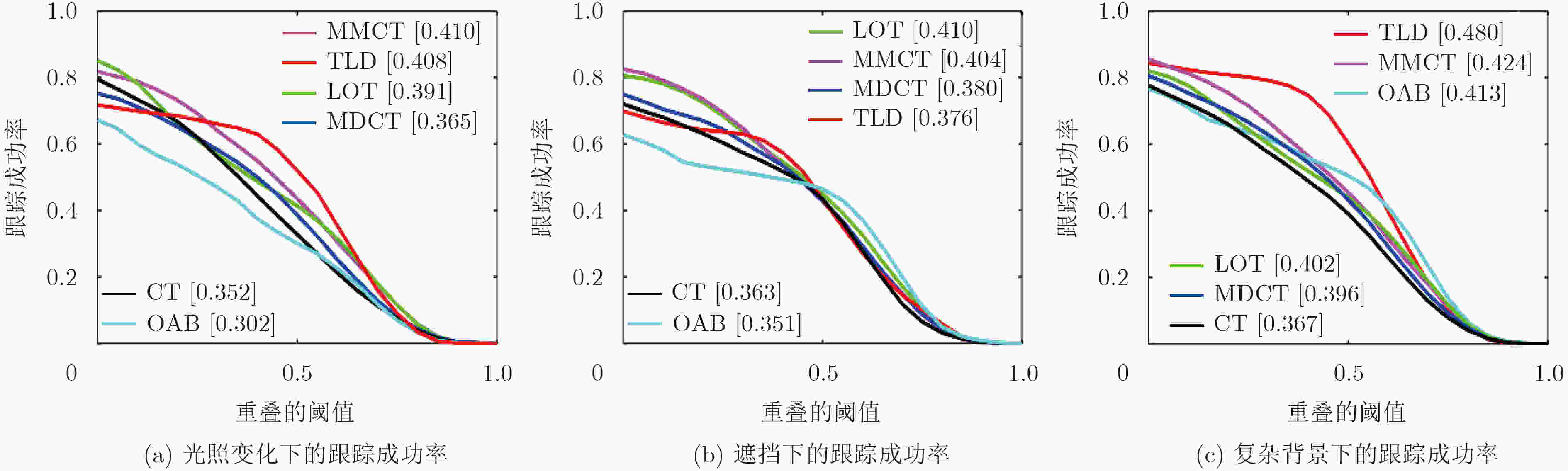
图像序列 TLD[8] LOT[5] OAB[7] CT[9] MDCT[10] MMCT Fish 0.49 0.25 0.44 0.21 0.48 0.45 Sylvester 0.63 0.52 0.57 0.60 0.49 0.57 Faceocc1 0.55 0.40 0.17 0.68 0.70 0.66 Boy 0.57 0.41 0.75 0.30 0.28 0.24 Basketball 0.07 0.45 0.05 0.13 0.11 0.28 Football 0.56 0.54 0.41 0.09 0.27 0.64 平均成功率 0.48 0.43 0.40 0.34 0.39 0.47 表 3 中心偏差率及平均帧率
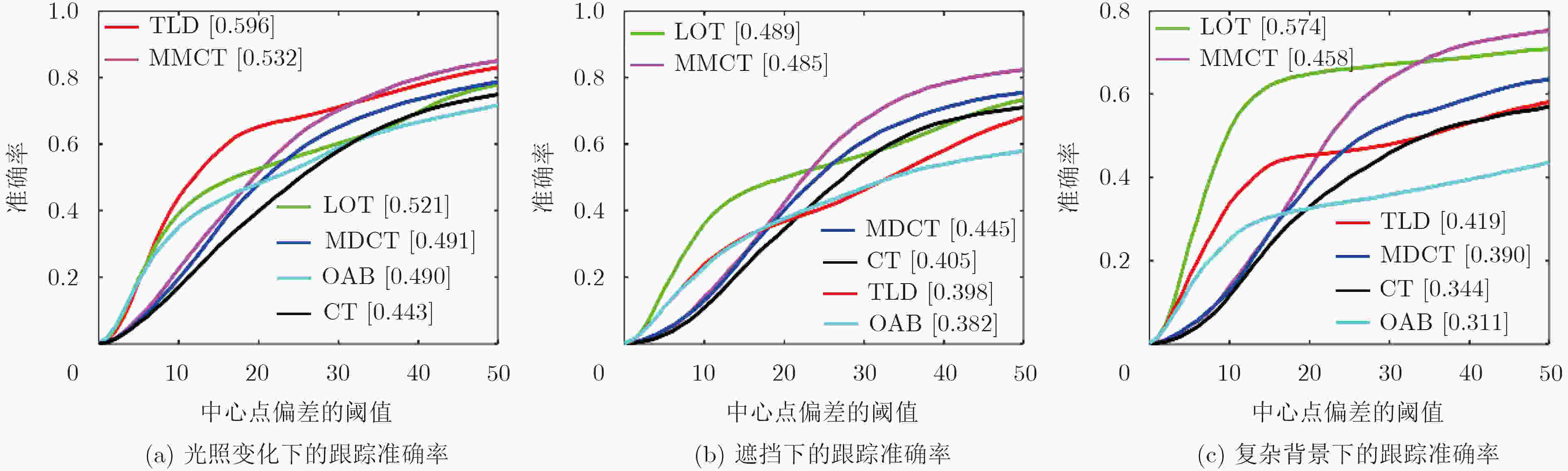
图像序列 TLD LOT OAB CT MDCT MMCT Fish 13.20 29.30 22.50 41.85 26.41 24.69 Sylvester 10.39 13.10 13.40 12.12 18.64 14.00 Faceocc1 30.63 34.20 89.34 21.81 21.16 23.92 Boy 7.91 72.34 3.70 20.21 60.66 66.65 Basketball 127.97 69.28 141.02 91.79 145.18 45.77 Football 13.40 9.21 22.63 227.90 23.59 7.4 平均偏差率 33.92 37.91 48.77 69.30 49.27 30.41 平均帧率 15.92 0.48 5.26 74.70 72.85 74.60 -
郁道银, 王悦行, 陈晓冬, 等. 基于随机投影和稀疏表示的跟踪算法[J]. 电子与信息学报, 2016, 38(7): 1602–1608 doi: 10.11999/JEIT151064YU Daoyin, WANG Yuexing, CHEN Xiaodong, et al. Visual tracking based on random projection and sparse representation[J]. Journal of Electronics&Information Technology, 2016, 38(7): 1602–1608 doi: 10.11999/JEIT151064 田鹏, 吕江花, 马世龙, 等. 基于局部差别性分析的目标跟踪算法[J]. 电子与信息学报, 2017, 39(11): 2635–2643 doi: 10.11999/JEIT170045TIAN Peng, LÜ Jianghua, MA Shilong, et al. Robust object tracking based on local discriminative analysis[J]. Journal of Electronics&Information Technology, 2017, 39(11): 2635–2643 doi: 10.11999/JEIT170045 COLLINS R T. Mean-shift blob tracking through scale space[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Madison, USA, 2003, 2: 234–240. ADAM A, RIVLIN E, and SHIMSHONI I. Robust fragments-based tracking using the integral histogram[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New York, USA, 2006, 1: 798–805. doi: 10.1109/CVPR.2006.256. ORON S, BAR-HILLEL A, LEVI D, et al. Locally orderless tracking[J]. International Journal of Computer Vision, 2015, 111(2): 213–228 doi: 10.1007/s11263-014-0740-6 BABENKO B, YANG M H, and BELONGIE S. Robust object tracking with online multiple instance learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1619–1632 doi: 10.1109/TPAMI.2010.226 GRABNER H, GRABNER M, and BISCHOF H. Real-time tracking via on-line boosting[C]. Proceedings of the British Machine Vision Conference, Edinburgh, UK, 2006: 47–56. KALAL Z, MIKOLAJCZYK K, and MATAS J. Tracking-learning-detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1409–1422 doi: 10.1109/TPAMI.2011.239 ZHANG Kaihua, ZHANG Lei, and YANG M H. Real-time compressive tracking[C]. Proceedings of the European Conference on Computer Vision, Florence, Italy, 2012: 864–877. doi: 10.1007/978-3-642-33712-3_62. SUN Hang, LI Jing, CHANG Jun, et al. Efficient compressive sensing tracking via mixed classifier decision[J]. Science China Information Sciences, 2016, 59(7): 072102 doi: 10.1007/s11432-015-5424-5 HELD D, THRUN S, and SAVARESE S. Learning to track at 100 fps with deep regression networks[C]. Proceedings of the European Conference on Computer Vision, Amsterdam, Netherlands, 2016: 749–765. doi: 10.1007/978-3-319-46448-0_45. NAM H and HAN B. Learning multi-domain convolutional neural networks for visual tracking[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 4293–4302. doi: 10.1109/CVPR.2016.465. SONG Yibin, MA Chao, GONG Linjun, et al. CREST: Convolutional residual learning for visual tracking[C]. Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 2017: 2555–2564. doi: 10.1109/ICCV.2017.279. WU Yi, LIM J, and YANG M H. Online object tracking: A benchmark[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, USA, 2013: 2411–2418. doi: 10.1109/CVPR.2013.312. DIACONIS P and FREEDMAN D. Asymptotics of graphical projection pursuit[J]. Annals of Statistics, 1984, 12(3): 793–815 doi: 10.1214/aos/1176346703 HARE S, GOLODETZ S, SAFFARI A, et al. Struck: Structured output tracking with kernels[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(10): 2096–2109 doi: 10.1109/TPAMI.2015.2509974 -





 下载:
下载:



 下载:
下载:
