基于q 梯度的仿射投影算法及其稳态均方收敛分析

王世元; 史春芬; 蒋云翔; 王文月; 钱国兵

doi:10.11999/JEIT171125

基于q 梯度的仿射投影算法及其稳态均方收敛分析

doi: 10.11999/JEIT171125

王世元^{1, 2, ,},
史春芬^{1, 2},
蒋云翔³,
王文月^{1, 2},
钱国兵^{1, 2}

1.
西南大学电子信息工程学院重庆 400715
2.
重庆非线性电路和智能信息处理重点实验室重庆 400715
3.
清华大学深圳研究生院深圳 518055

基金项目: 国家自然科学基金(61671389, 61701419)，中国博士后基金(2017M610583, 2017M620783)，重庆博士后科研基金(Xm2017107, Xm2017104)

详细信息

作者简介:
王世元：男，1980年生，教授，硕士生导师，研究方向为自适应信号处理、非线性滤波器设计、混沌通信系统

史春芬：女，1990年生，硕士生，研究方向为信号与信息处理

蒋云翔：男，1986年生，博士，研究方向为无线通信、无线能量信息同传、全双工通信

王文月：女，1994年生，硕士生，研究方向为信号与信息处理

钱国兵：男，1986年生，讲师，研究方向为自适应信号处理

通讯作者:
王世元　 wsy@swu.edu.cn

中图分类号: TN911.72
计量
- 文章访问数: 1654
- HTML全文浏览量: 653
- PDF下载量: 81
- 被引次数: 0
出版历程
- 收稿日期: 2017-11-28
- 修回日期: 2018-06-14
- 网络出版日期: 2018-07-30
- 刊出日期: 2018-10-01

q -affine Projection Algorithm and Its Steady-state Mean Square Convergence Analysis

Shiyuan WANG^{1, 2
, ,},
Chunfen SHI^{1, 2},
Yunxiang JIANG³,
Wenyue WANG^{1, 2},
Guobing QIAN^{1, 2}

1.
College of Electronic and Information Engineering, Southwest University, Chongqing 400715, China
2.
Chongqing Key Laboratory of Nonlinear Circuits and Intelligent Information Processing, Chongqing 400715, China
3.
Graduate School at Shenzhen of Tsinghua University, Shenzhen 518055, China

Funds: The National Natural Science Foundation of China (61671389, 61701419), China Postdoctoral Science Foundation Funded Project (2017M610583, 2017M620783), Chongqing Postdoctoral Science Foundation Special Funded Project (Xm2017107, Xm2017104)

摘要

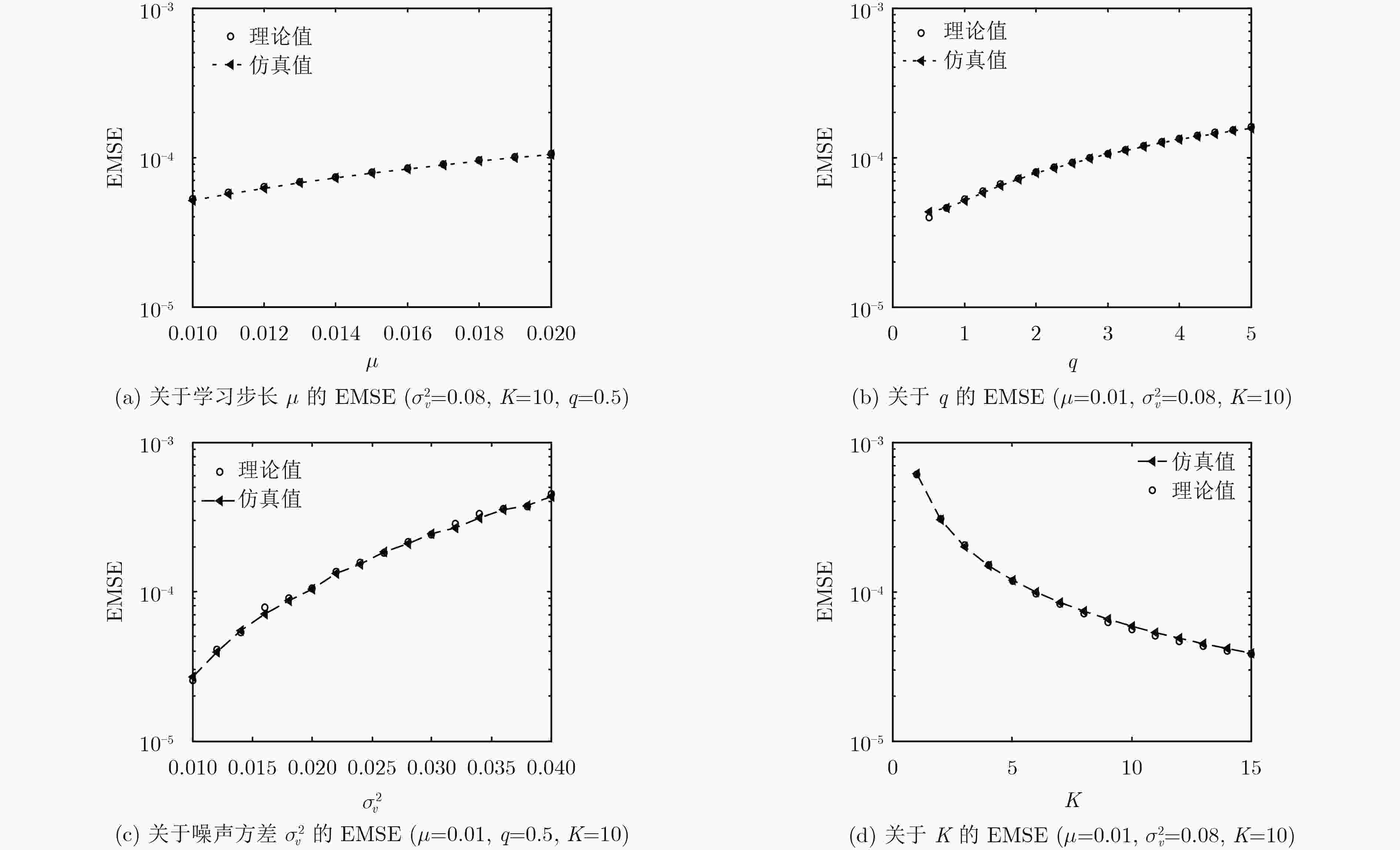
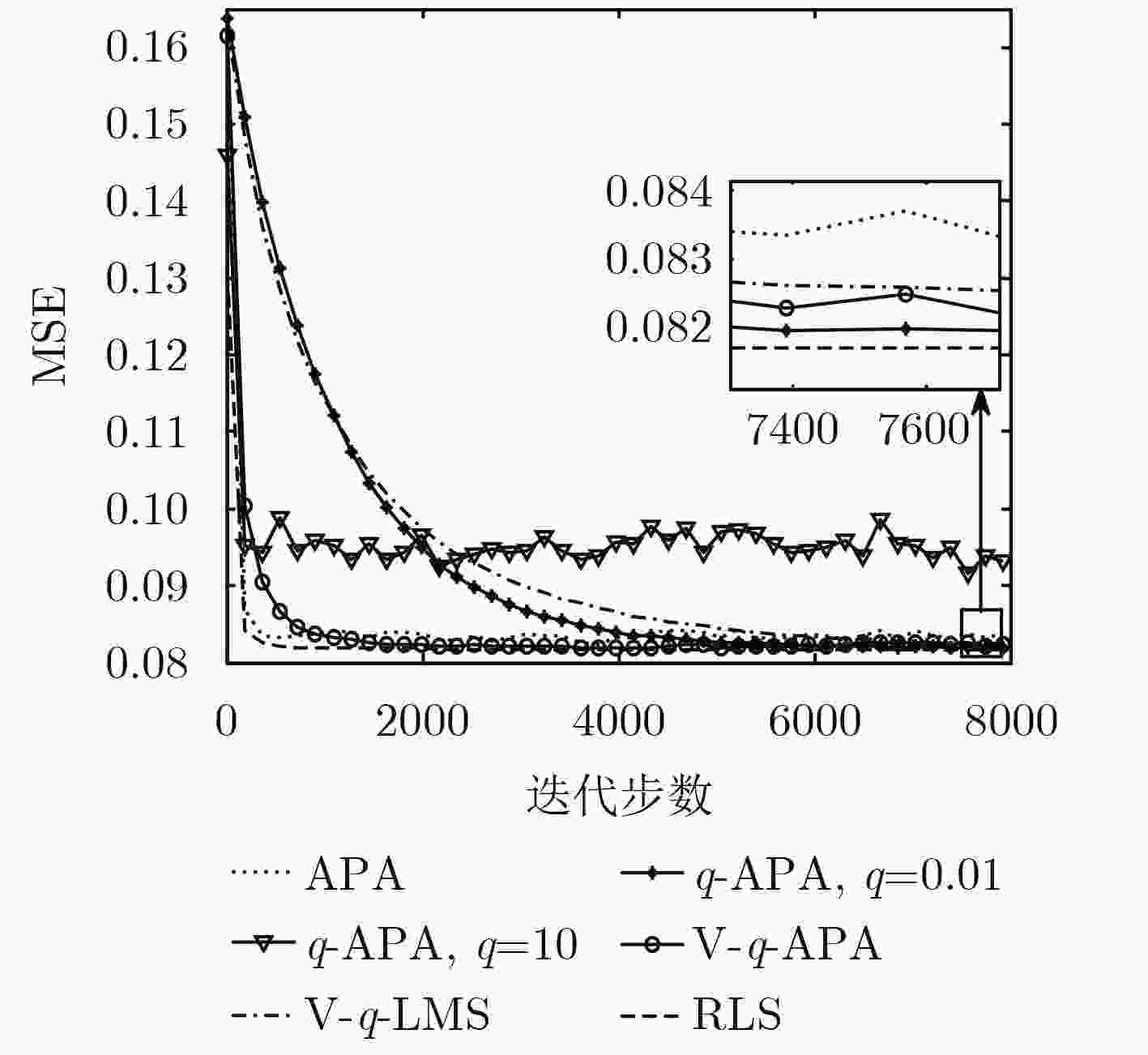
摘要: q梯度是基于q微分的广义梯度。为了进一步提高仿射投影算法(APA)的滤波性能，该文基于最小均方误差准则将q梯度应用于APA进而产生一种新的q-APA，在高斯噪声环境下选择合适的q值可以取得理想的滤波性能。通过理论分析，提出了保证算法收敛的充分条件，并计算出表征滤波性能的稳态额外均方误差(EMSE)。除此之外，为了进一步提高算法的滤波性能，提出一个变q的APA(V-q-APA)。在高斯噪声环境下，将q-APA和V-q-APA应用于系统辨识中。仿真结果表明：与传统的APA和变q的最小化均方(V-q-LMS)算法相比，q-APA和V-q-APA均具有更好的滤波性能。
- 信号处理 /
- q微分 /
- 误差准则 /
- 仿射投影算法 /
- 均方收敛分析
Abstract: The q-gradient is a generalized gradient based on the q-derivative concept. To improve the filtering performance of the Affine Projection Algorithm (APA), the q-gradient is applied to APA based on the minimum of the recent mean square errors, generating a novel q-Affine Projection Algorithm (q-APA). The q-APA with appropriate setting of q achieves desirable filtering performance in the presence of Gaussian noises. A sufficient condition for guaranteeing convergence of the proposed q-APA is also presented, and its steady-state Excess Mean Square Error (EMSE) of q-APA is obtained theoretically to evaluate the filtering performance. In addition, the Variable q-APA (V-q-APA) is developed to improve further the filtering performance. Simulations in the context of system identification demonstrate the superior filtering performance of the proposed algorithms compared with APA and Variable q-Least Mean Square (V-q-LMS) algorithm in the presence of Gaussian noise.
- Signal processing /
- q-derivative /
- Error criterion /
- Affine Projection Algorithm (APA) /
- Mean square convergence analysis

HTML全文

图 1 高斯噪声环境下q-APA算法的理论和仿真

下载: 全尺寸图片幻灯片

图 2 V-q-APA算法和其他不同算法的学习曲线

下载: 全尺寸图片幻灯片

表 1 基于100次蒙特卡罗仿真的各个算法的性能比较

算法	MSE	时间(s)
APA	0.0835	10.0802
q-APA (q=10)	0.0951	10.9385
q-APA (q=0.01)	0.0819	10.9385
V-q-LMS	0.0825	15.0982
V-q-APA	0.0820	15.8802
RLS	0.0818	12.0637

下载: 导出CSV

参考文献(16)

HUANG Y T, BENESTY J, and CHEN J D. Acoustic MIMO Signal Processing[M]. Bosten, MA: Spring, 2006: 233–236.

刘建成, 赵宏志, 全厚德, 等. 迭代变步长LMS算法及性能分析[J]. 电子与信息学报, 2015, 37(7): 1674–1680 doi: 10.11999/JEIT141501

LIU Jiancheng, ZHAO Hongzhi, QUAN Houde, et al. Iteration-based variable step-size LMS algorithm and its performance analysis[J]. Journal of Electronics&Information Technology, 2015, 37(7): 1674–1680 doi: 10.11999/JEIT141501

贾冲, 郭明嘉, 张雄伟. 基于M估计变步长自适应仿射投影算法的稳健时延估计[J]. 电子与信息学报, 2008, 30(5): 1080–1083 doi: 10.3724/SP.J.1146.2006.01718

JIA Chong, GUO Mingjia, and ZHANG Xiongwei. Robust time delay estimation using variable step-size affine projection algorithm with M-estimator[J]. Journal of Electronics&Information Technology, 2008, 30(5): 1080–1083 doi: 10.3724/SP.J.1146.2006.01718

SAYED A H. Fundamentals of Adaptive Filtering[M]. New York: Wiley Interscience, 2003: 77–79.

RUPP M. Convergence properties of adaptive equalizer algorithms[J]. IEEE Transaction on Signal Processing, 2011, 59(6): 2562–2574 doi: 10.1109/TSP.2011.2121905

QIAO Bingqiang, LIU Siming, ZENG Houdun, et al. Evaluation of dimension of fractal time series with the least mean square method[J]. SCIENCE CHINA Physics Mechanics&Astronomy, 2017, 60(4): 040521 doi: 10.1007/s11433-016-9002-8

毕严先, 魏少明, 王俊, 等. 基于最小二乘估计的InISARS空间目标三维成像方法[J]. 电子与信息学报, 2016, 38(5): 1079–1084 doi: 10.11999/JEIT151000

BI Yanxian, WEI Shaoming, WANG Jun, et al. Interferometric ISAR imaging for 3-D geometry of uniformly rotating targets based on least mean squares estimation method[J]. Journal of Electronics&Information Technology, 2016, 38(5): 1079–1084 doi: 10.11999/JEIT151000

汤光明, 孙艺, 徐潇雨, 等. 动态更新失真代价的自适应JPEG隐写算法[J]. 通信学报, 2017, 38(9): 1–8 doi: 10.11959/j.issn.1000-436x.2017177

TANG Guangming, SUN Yi, XU Xiaoyu, et al. Adaptive JPEG implicit algorithm for dynamic update distortion cost[J]. Journal on Communications, 2017, 38(9): 1–8 doi: 10.11959/j.issn.1000-436x.2017177

王奇, 陈航, 王英民, 等. 基于最小二乘的短垂线阵匹配场处理[J]. 电子与信息学报, 2017, 39(6): 1355–1362 doi: 10.11999/JEIT160727

WANG Qi, CHEN Hang, WANG Yingmin, et al. Matched filed processing based on the least squares algorithm for short vertical linear array[J]. Journal of Electronics&Information Technology, 2017, 39(6): 1355–1362 doi: 10.11999/JEIT160727

ERNST T. The History of q-Calculus and a New Method[M]. Uppsala: Uppsala University Press, 2000: 40–103.

AL-SAGGAF U M, MOINUDDIN M, ARIF M, et al. The q-least mean square algorithm[J]. Signal Processing, 2015, 111(C): 50–60 doi: 10.1016/j.sigpro.2014.11.016

SOTERRONI A C, GALSKI R L, and RAMONS F M. The q-gradient method for global optimization[J]. Mathematics, 2012, 1558(1): 2389–2393 doi: 10.1063/1.4826022

练秋生, 齐秀梅, 陈书贞, 等. 基于结构稀疏性的单次曝光相位成像算法[J]. 电子与信息学报, 2017, 39(7): 1546–1553 doi: 10.11999/JEIT161171

LIAN Qiusheng, QI Xiumei, CHEN Shuzhen, et al. Single-shot phase imagine algorithm based on structural sparsity[J]. Journal of Electronics&Information Technology, 2017, 39(7): 1546–1553 doi: 10.11999/JEIT161171

SHIN H C and SAYED A H. Mean-square performance of a family of affine projection algorithms[J]. IEEE Transactions on Signal Processing, 2004, 52(1): 90–102 doi: 10.1109/TSP.2003.820077

CHEN Badong, XING Lei, LIANG Junli, et al. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion[J]. IEEE Signal Processing Letters, 2014, 21(7): 880–884 doi: 10.1109/LSP.2014.2319308

LIU Chunhui, QI Yue, and DING Wenrui. The data-reusing MCC-based algorithm and its performance analysis[J]. Chinese Journal of Electronics, 2016, 25(4): 719–725 doi: 10.1049/cje.2016.06.019

施引文献

资源附件(0)

访问统计