Online Mapping Algorithm Based on Reliability for 5G Network Slicing
-
摘要: 为了满足业务多样性对5G网络切片带来差异化需求的同时保证切片的可靠性,实现网络资源的优化配置。该文针对5G网络切片的动态映射、轻量级可靠映射问题,提出对计算资源、链路资源和RRU频谱资源联合分配方案。首先,该方案建立面向可靠性约束的多目标资源分配模型,引入李雅普诺夫优化模型,在保证队列稳定同时优化资源分配。其次,提出了基于队列稳定性的虚拟节点映射算法和基于可靠性的虚拟链路映射算法。最后,将时间离散为一系列连续的时间窗,利用时间窗动态处理到达的网络切片请求,实现在线的网络切片映射算法。仿真结果表明,该算法提高了资源利用率,并且保证网络可靠性。Abstract: To meet the diversified demand of 5G Network Slicing (NS), while ensuring the reliability of slice, to achieve the optimal allocation of network resources, considering the dynamic mapping and lightweight reliable mapping problem of network slicing, this paper proposes a joint allocation scheme of computing resources, link resources and the spectrum resources of Radio Remote Unit (RRU). Firstly, a multi-objective resource allocation model oriented to reliability constraints is established, and the Lyapunov optimization model is introduced to ensure the queue stability and optimize the resource allocation. Then, the virtual node mapping algorithm based on queue stability and virtual link mapping algorithm based on reliability are proposed. Finally, the time is discretized into a series of continuous time windows, and the online network slice mapping algorithm is implemented by using the time window dynamic processing of the incoming network slice request. Simulation results show that the proposed algorithm improves resource utilization and guarantees network reliability.
-
Key words:
- Network Slicing (NS) /
- Resource allocation /
- Reliability /
- Lyapunov optimization
-
表 1 基于队列稳定性的虚拟节点映射
算法1 基于队列稳定性的虚拟节点映射 (1) 虚拟切片 $\small G_v^g = \left( {N_v^g,E_v^g} \right)$
(2) 生成物理网络 $\small {G_s} = \left( {N_s,E_s} \right)$
(3) for all $\small n \in N_v^g$, do
(4) if $\small {C_n} > {C_i},\forall i \in {N_s}$ then
(5) 拒绝 $\small G_v^g,{y_g} = 0$
(6) return
(7) end if
(8) for all $\small i \in {N_s}|{C_n} \ge {C_i}$ do
(9) $\small {Y_i} \leftarrow \left\{ {V{p_g} - {Z_g}\left( t \right){w_{g,i}}{Q_i}\left( t \right)} \right\} + {Q_i}\left( t \right){\mu _i}\left( t \right)$
(10) $\small \varphi \left( i \right) \leftarrow 0,{y_g} \leftarrow 1$
(11) $\small {w_{g,i}} = {{{C_n}y_n^i} \Bigr/ {{P_g}}} = {{{C_{{s_{kg}}}}y_{{s_{kg}}}^i} \Bigr/ {{P_g}}} = {{{C_{{d_{kg}}}}y_{{d_{kg}}}^j} \Bigr/ {{P_g}}}\left( {i \ne j} \right)$
(12) end for
(13) Let $\small {i_{\max }} = \mathop {\arg \max }\limits_{i \in {N_s}} \left\{ {{Y_i}\left| {\varphi \left( i \right) = 0} \right.} \right\}$
(14) set $\small y_g^{{i_{\max }}} \leftarrow 1$, $\small \varphi \left( {{i_{\max }}} \right) \leftarrow 1$, $\small {Y_g} \leftarrow {i_{\max }}$
(15) end for
(16) 基于 $\small {Y_g}$利用VLM-R(基于可靠性的链路映射算法)映射虚拟链路
(17) VLM-R成功映射 then
(18) 更新物理网络剩余的资源容量
(19) else
(20) 拒绝 $\small G_v^g,{y_g} = 0$
(21) end if表 2 基于切片可靠性的虚拟链路映射
算法2 基于切片可靠性的虚拟链路映射 Input: Request $\small G_v^g = \left( {N_v^g,E_v^g,{T_g},{b_g}} \right)$, $\small {G_s} = \left( {{N_s},{E_s},{\lambda _s}} \right)$, $\small {Y_g}$,
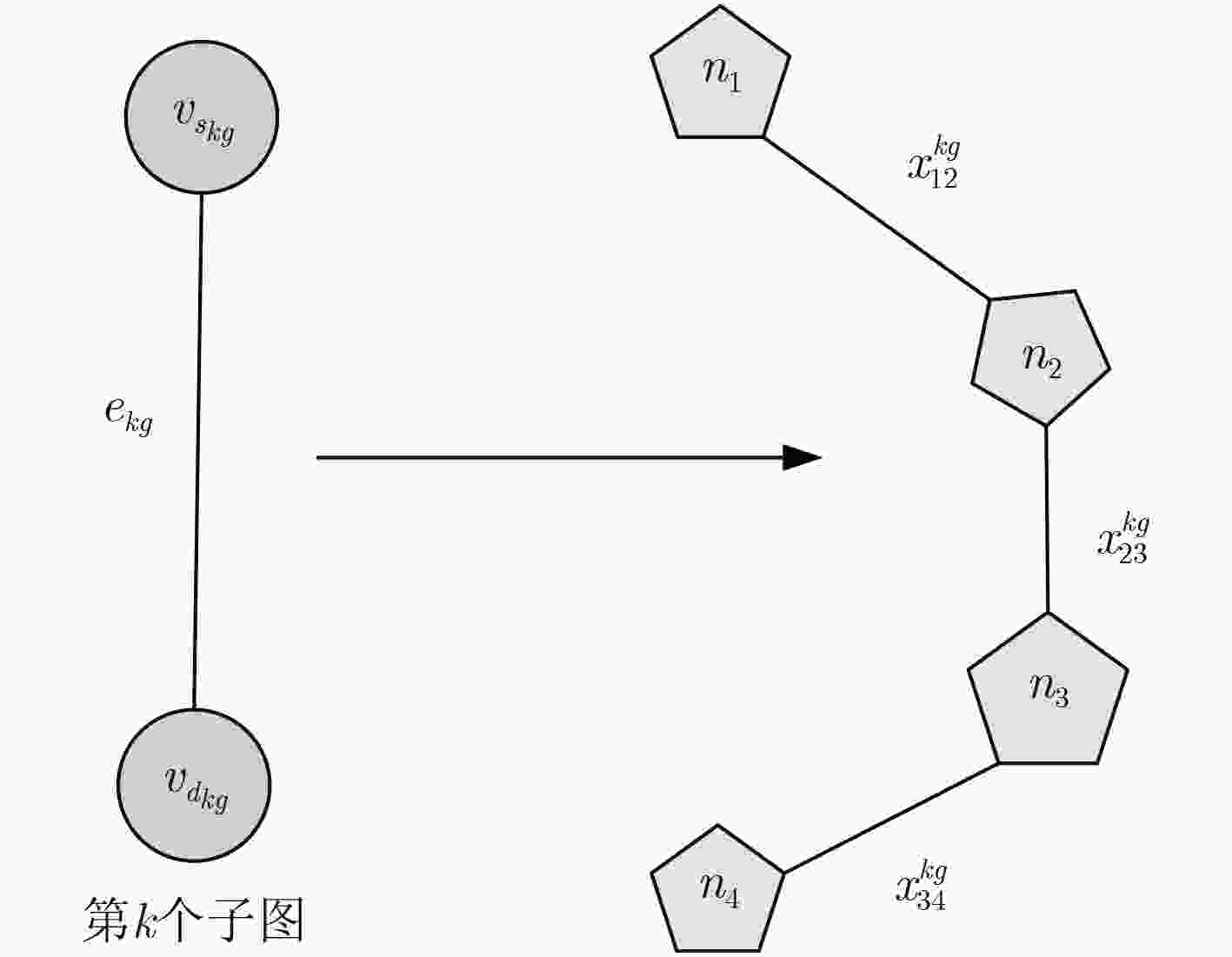
$\small {e_{kg}} = \left( {{\rm{src}}{{\scriptsize{\_} }}{\rm{id}},{\rm{dst}}{\scriptsize{\_}}{\rm{id}}} \right)$
For $\small {e_{kg}} \in E_v^g$
Begin:
(1) 将每个切片中的虚拟链路按照k递增的顺序排列
(2) for each $\small {e_{kg}} \in E_v^g$ do
(3) 由算法1得到的 $\small {Y_g}$为 $\small {e_{kg}}$匹配相对应的物理节点 $\small {n_s}$与 $\small {n_t}$
(4) set $\small {\rm{src}}{\scriptsize{\_}}{\rm{id}} \leftarrow {n_s},{\rm{dst}}{\scriptsize{\_}}{\rm{id}} \leftarrow {n_t}$
(5) 计算所有从 $\small {\rm{src}}{\scriptsize{\_}}{\rm{id}}$到 $\small {\rm{dst}}{\scriptsize{\_}}{\rm{id}}$的子路径 $\small {P_m} \in \Omega \left( {{e_{kg}}} \right)$
(6) end for
(7) for each 子路径 $\small {P_m} \in \Omega \left( {{e_{kg}}} \right)$ do
(8) if $\small \left\{ {{b_{ij}} < {b_k}\left| {{l_{ij}} \in {P_m}} \right.} \right\}$ then
(9) refuse $\small {e_{kg}}$
(10) else $\small x_{ij}^{kg} = 1,\forall {l_{ij}} \in {P_m}$
(11) 计算此路径 $\small {P_m}$的失效率 $\small \sum\nolimits_{i,j} \!\! {x_{ij}^{kg}} {\lambda _{ij}}{T_g}$作为它的权值
(12) end if
(13) for all $\small {p_k}$ do
(14) $\small {\lambda _k} \leftarrow \sum\nolimits_{i,j} {x_{ij}^{kg}} {\lambda _{ij}}{T_g}$
(15) end for
(16) let $\small {p_{\min }} = \mathop {\arg \min }\limits_{{p_m} \in \Omega \left( {{e_{kg}}} \right)} \left\{ {{\lambda _k}} \right\}$
(17) set $\small X_{ij}^{kg} \leftarrow x_{ij}^{kg}$
(18) end for表 3 基于时间窗的在线网络切片映射
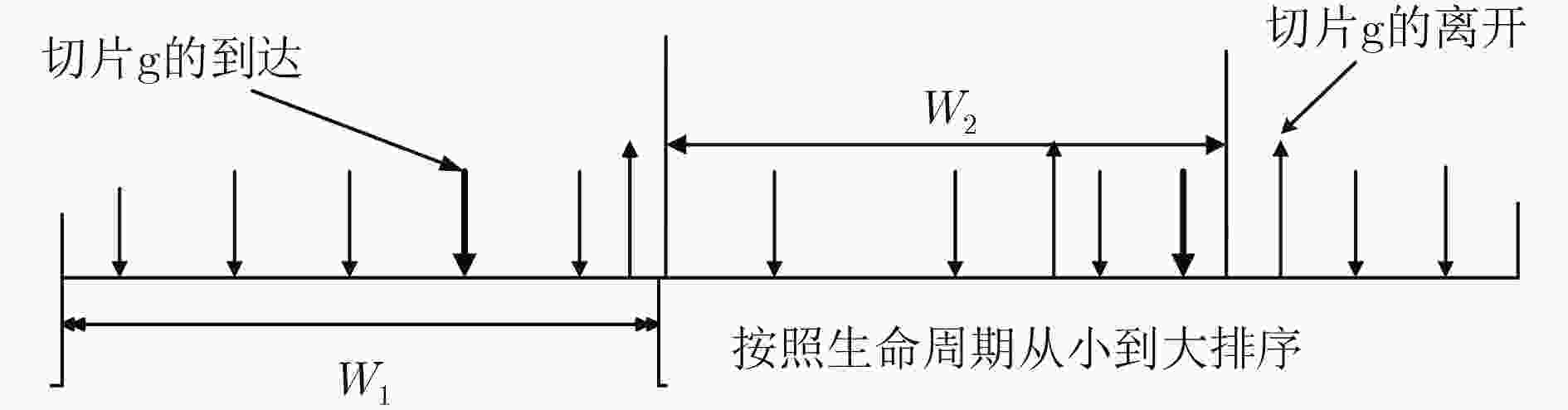
算法3 基于时间窗的在线网络切片映射 (1) 初始化时间窗为空集 $\small {W_1} \leftarrow \left\{ {} \right\}$ (2) loop (3) $\small {W_2} \leftarrow {W_1}$ (4) $\small {W_1} \leftarrow \left\{ {} \right\}$ (5) repeat (6) 添加新的虚拟切片请求 $\small G_v^g = \left( {N_v^g,E_v^g,{T_g}} \right)$到 $\small {W_2}$ (7) until 当前窗口 $\small {W_2}$过期 (8) 根据切片生命周期对 $\small {W_2}$内的切片进行排序,时间周期越短越优 先处理 (9) 将当前的时间 $\small {T_2} \leftarrow {\rm{Current}}\;{\rm{time}}$ (10) for all $\small G_v^g \in {W_2}$ do (11) if $\small {t_w}\left( {G_v^g} \right)$在 $\small {T_2}$之前已经过期 then (12) Reject $\small G_v^g$ (13) else (14) 映射 $\small G_v^g$用算法1 (15) if 算法1映射 $\small G_v^g$失败 then (16) 将 $\small G_v^g$添加到 $\small {W_1}$ (17) end if (18) end if (19) end for (20) end loop -
CAO Hantong, ZHU Yongxu, ZHENG Gan, et al. A novel optimal mapping algorithm with less computational complexity for virtual network embedding[J]. IEEE Transactions on Network and Service Management, 2018, 15 (1): 356-371. DOI: 10.1109/TNSM.2017.2778106. ZHOU Zibo, CHANG Xiaolin, YANG Yang, et al. Resource-aware virtual network parallel embedding based on genetic algorithm[C]. 2016 17th International Conference on Parallel and Distributed Computing, Applications and Technologies, Guangzhou, 2016: 81–86. ZHENG Hongkun, LI Jingjing, GONG Yuejiao, et al. Link mapping-oriented ant colony system for virtual network embedding[C]. 2017 IEEE Congress on Evolutionary Computation, San Sebastian, 2017: 1223–1230. TRIVISCONNO R, VAISHNAVI I, and GUERZONI R. Virtual links mapping in future SDN-enabled networks[C]. IEEE SDN for Future Networks and Services, Trento, 2013: 1–5. CHOWDHURY M, RAHMAN M R, and BOUTABA R. ViNEYard: Virtual network embedding algorithms with coordinated node and link mapping[J]. IEEE/ACM Transactions on Networking, 2012, 20(1): 206-219. GUERZONI R, DESPOTOVIC Z, and TRIVISONNO R. Modeling reliability requirements in coordinated node and link mapping[C]. IEEE 33rd International Symposium on Reliable Distributed Systems, Nara, 2014: 321–330. LONG Q, ASSI C, SHABAN K, et al. A Reliability-aware network service chain provisioning with delay guarantees in NFV-enabled enterprise datacenter networks[J]. IEEE Transactions on Network & Service Management, 2017, 14(3): 554-568. DOI: 10.1109/TNSM.2017.2723090. SHAHRIAR N, AHMED R, CHOWDHURY S, et al. Generalized recovery from node failure in virtual network embedding[J]. IEEE Transactions on Network and Service Management, 2017, 14(2): 261-274. DOI: 10.1109/TNSM.2017.2693404. HA V N and LONG B L. End-to-end network slicing in virtualized OFDMA-based cloud radio access networks[J]. IEEE Access, 2017, 5: 18675-18691.DOI: 10.1109/ACCESS.2017.2754461. 唐伦, 张亚, 梁荣, 等.基于网络切片的网络效用最大化虚拟资源分配算法[J]. 电子与信息学报, 2017, 39(8): 1812-1818. DOI: 10.11999/JEIT161322.TANG Lun, ZHANG Ya, LIANG Rong, et al. Virtual resource allocation algorithm for network utility maximization based on network slicing[J]. Journal of Electronics & Information Technology, 2017, 39(8): 1812-1818. DOI: 10.11999/JEIT161322. LI Kenli, TANG Xiaoyong, VEERAVALLI B, et al. Scheduling precedence constrained stochastic tasks on heterogeneous cluster systems[J]. IEEE Transactions on Computers, 2014, 64(1): 191-204. DOI: 10.1109/TC.2013.205 CHEN Yu and ZHANG Hongwei. Optimal request clustering for link reliability guarantee in wireless networked control[C]. IEEE Wireless Communications and Networking Conference, San Francisco, 2017: 1–6. LIU Jiajia, JIANG Zhongyuan, KATO N, et al. Reliability evaluation for NFV deployment of future mobile broadband networks[J]. IEEE Wireless Communications, 2016, 23(3): 90-96. DOI: 10.1109/MWC.2016.7498079. CASCAVAL P and FLORIA S A. SDP algorithm for network reliability evaluation[C]. IEEE International Conference on Innovations in Intelligent Systems and Applications, Gdynia, 2017: 119–125. KANG Jinkyu, SIMEONE O, and KANG J. On the trade-off between computational load and reliability for network function virtualization[J]. IEEE Communications Letters, 2017, 21(8): 1767-1770. DOI: 10.1109/LCOMM.2017.2698040. SHUMINOSKI T and JANEVSKI T. Lyapunov optimization framework for 5g mobile nodes with multi-homing[J]. IEEE Communications Letters, 2016, 20(5): 1026-1029. DOI: 10.1109/LCOMM.2016.2540622. -





 下载:
下载:



 下载:
下载:
