基于改进集合卡尔曼滤波方法的目标运动轨迹多源异步数据融合方法研究

张泽群; 任文娟; 付琨; 方继飞; 张跃

doi:10.11999/JEIT171115

基于改进集合卡尔曼滤波方法的目标运动轨迹多源异步数据融合方法研究

doi: 10.11999/JEIT171115

1.
中国科学院电子学研究所北京 100190
2.
中国科学院空间信息处理与应用系统技术重点实验室北京 100190

详细信息

作者简介:
张泽群：男，1990 年生，助理研究员，研究方向为反问题、模型优化、地理空间信息挖掘

任文娟：女，1982 年生，副研究员，研究方向为电子目标识别、数据挖掘

付琨：男，1976 年生，研究员，研究方向为计算机视觉与遥感图像理解、地理空间信息挖掘与可视化

方继飞：男，1989 年生，工程师，研究方向为轨迹分析

张跃：男，1990 年生，助理研究员，研究方向为计算机视觉与遥感图像理解

通讯作者:
张泽群　 zqzhang1@mail.ie.ac.cn

中图分类号: TP391
计量
- 文章访问数: 2379
- HTML全文浏览量: 686
- PDF下载量: 99
- 被引次数: 0
出版历程
- 收稿日期: 2017-11-28
- 修回日期: 2018-05-25
- 网络出版日期: 2018-07-12
- 刊出日期: 2018-09-01

Research on Multi-source and Asynchronous Data Fusion of Target Trajectory Based on the Modified Ensemble Kalman Filter Method

1.
Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
2.
Key Laboratory of Technology in Geo-spatial Information Processing and Application System, Chinese Academy of Science, Beijing 100190, China

摘要

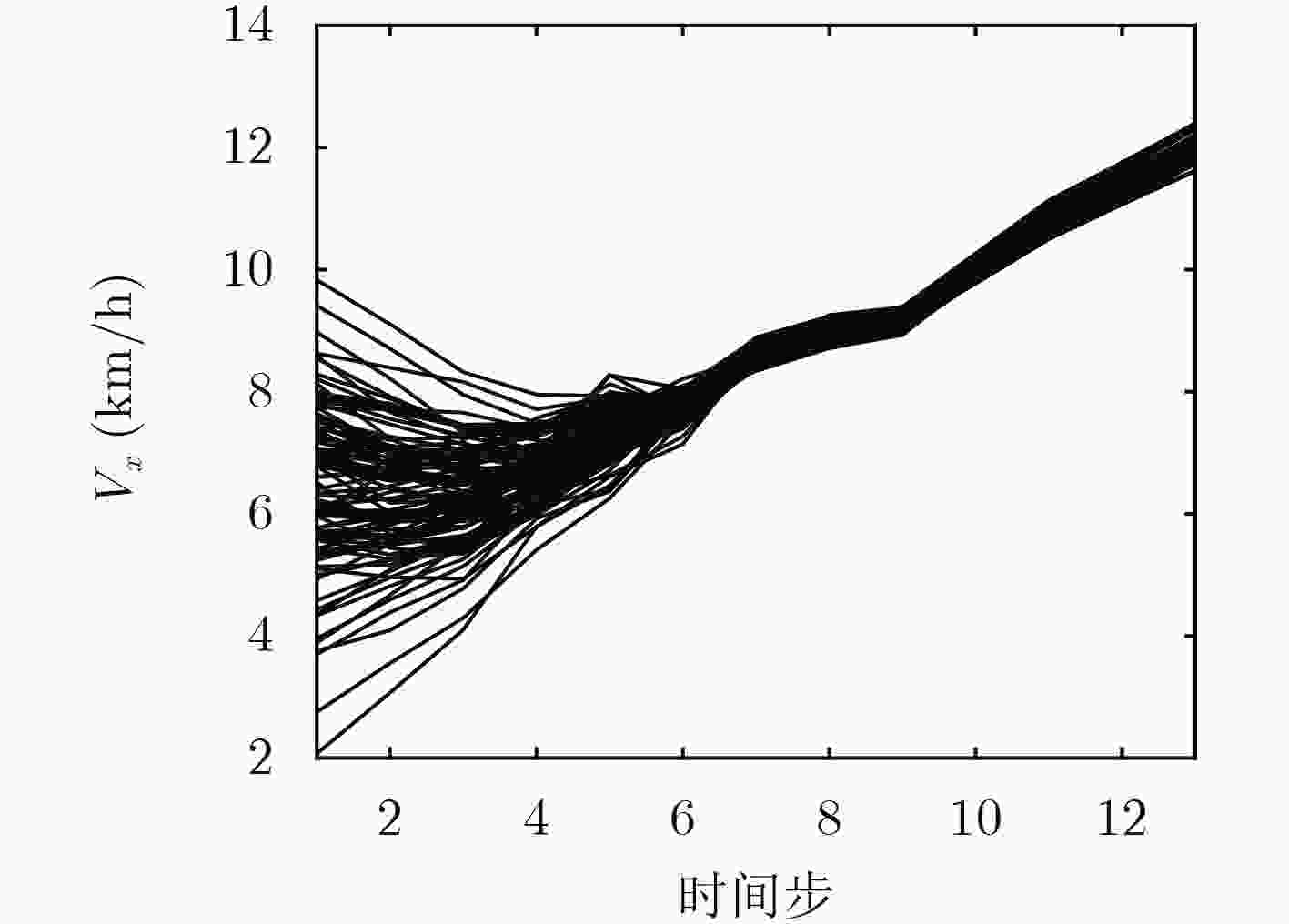
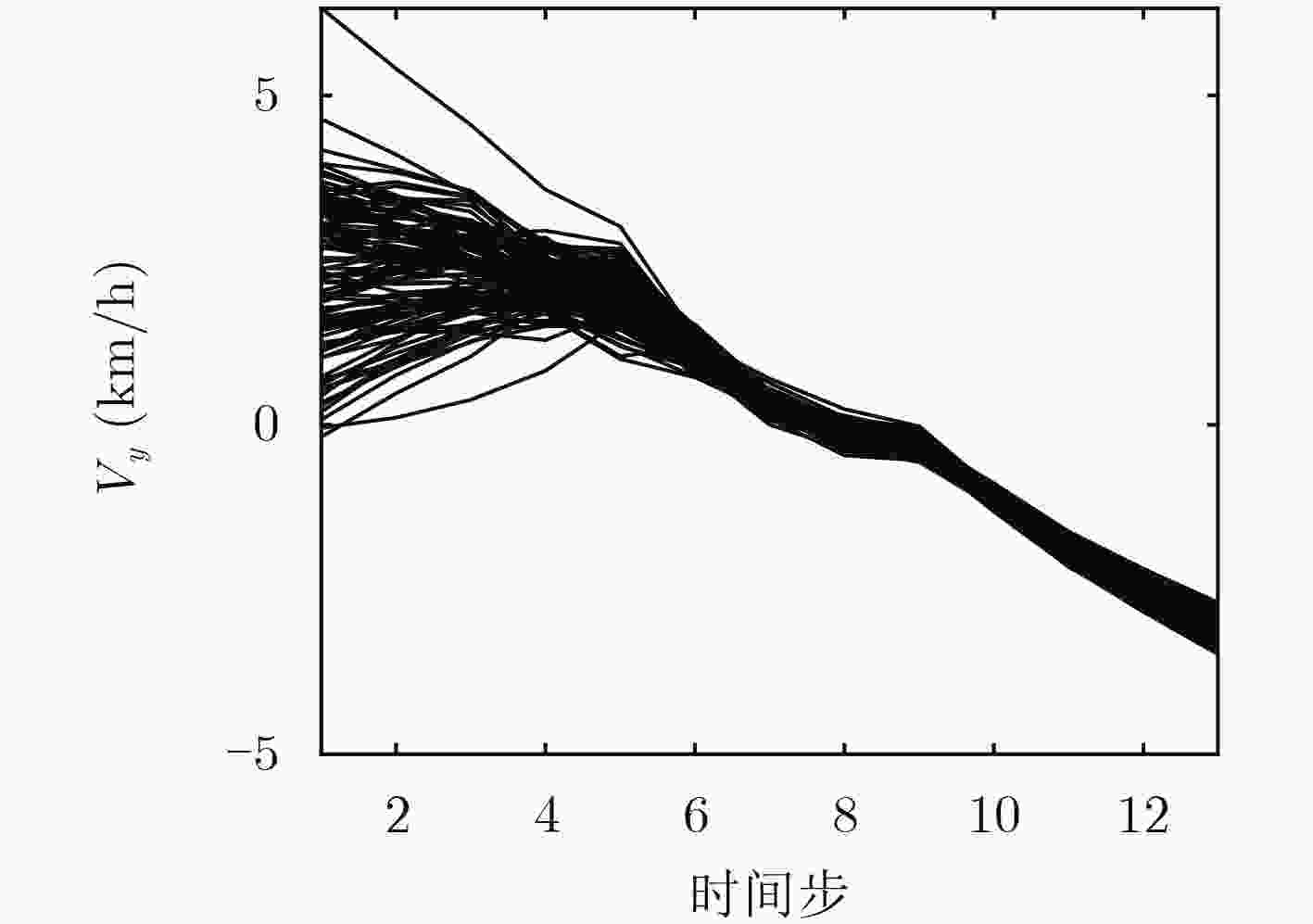
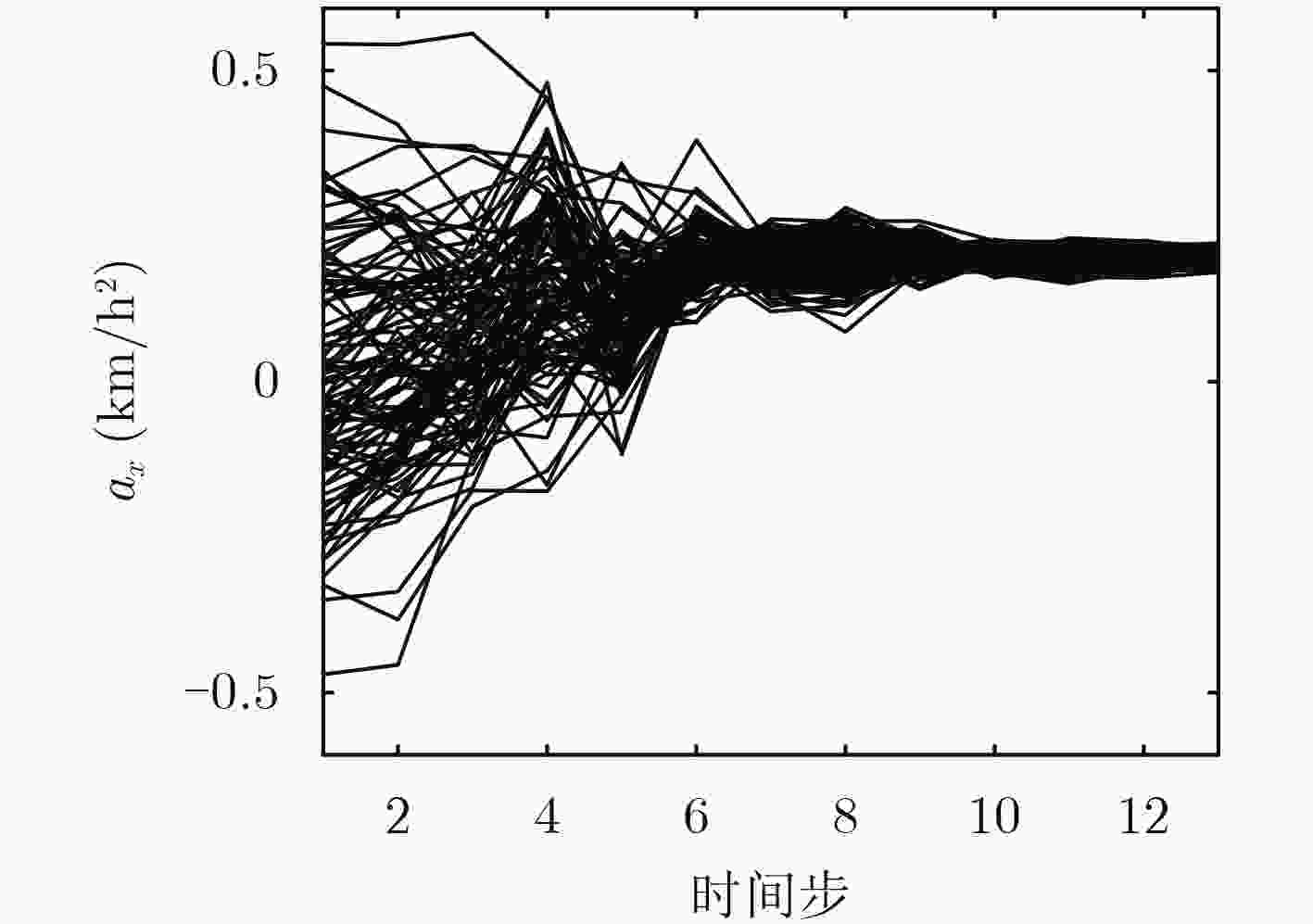
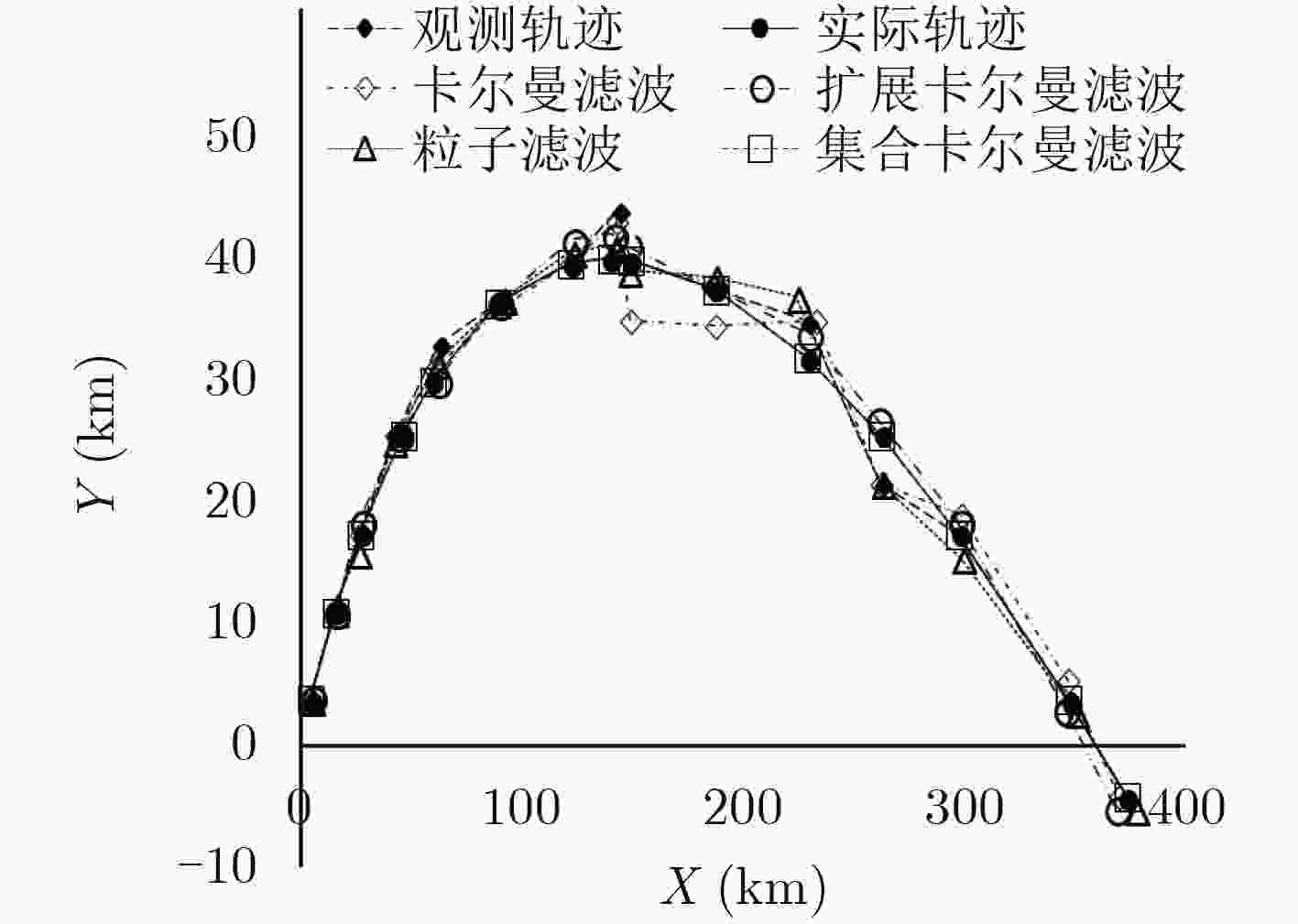
摘要: 该文构建了一个改进的多源异步观测数据情景下基于非线性运动学本构方程的集合卡尔曼滤波理论模型，该模型可以精确反演出目标运动状态参数(速度、加速度)以对目标后续运动进行预测。并基于集合卡尔曼滤波实现了多源观测数据融合，利用高精度观测数据修正低精度观测数据，修正后的数据精度可通过集合卡尔曼滤波提供的统计学信息进行标定，为非线性情形下目标轨迹多源异步数据融合问题提供了新的解决思路。
- 数据融合 /
- 目标轨迹分析 /
- 集合卡尔曼滤波
Abstract: A modified Ensemble Kalman Filter (EnKF) theory model based on kinematic equations is proposed to realize the historical fitting analysis and trajectory prediction of the target trajectory in the multi-source observation data scenario. This model is applied to accurately calculate the target motion state parameters (velocity and acceleration), then the target’s follow-up movement is predicted. The multi-source observation data fusion is realized by using the EnKF, which enables the low-precision observation data to be corrected by high-precision observation data, and the accuracy of the corrected data can be calibrated by the statistical information provided by the EnKF.
- Data fusion /
- Target trajectory analysis /
- Ensemble Kalman Filter (EnKF)

HTML全文

图 1 目标轨迹观测值和观测误差分布

下载: 全尺寸图片幻灯片

图 2 初始猜测值(速度、加速度)对目标轨迹的预测

下载: 全尺寸图片幻灯片

图 3 集合卡尔曼滤波实现目标轨迹的历史拟合

下载: 全尺寸图片幻灯片

图 4 集合卡尔曼滤波实现目标轨迹的历史拟合

下载: 全尺寸图片幻灯片

图 5 X方向速度集合卡尔曼滤波反演结果

下载: 全尺寸图片幻灯片

图 6 Y方向速度集合卡尔曼滤波反演结果

下载: 全尺寸图片幻灯片

图 7 X方向加速度集合卡尔曼滤波反演结果

下载: 全尺寸图片幻灯片

图 8 Y方向加速度集合卡尔曼滤波反演结果

下载: 全尺寸图片幻灯片

图 9 集合卡尔曼滤波运动拟合结果与卡尔曼滤波、扩展卡尔曼滤波和粒子滤波对比

下载: 全尺寸图片幻灯片

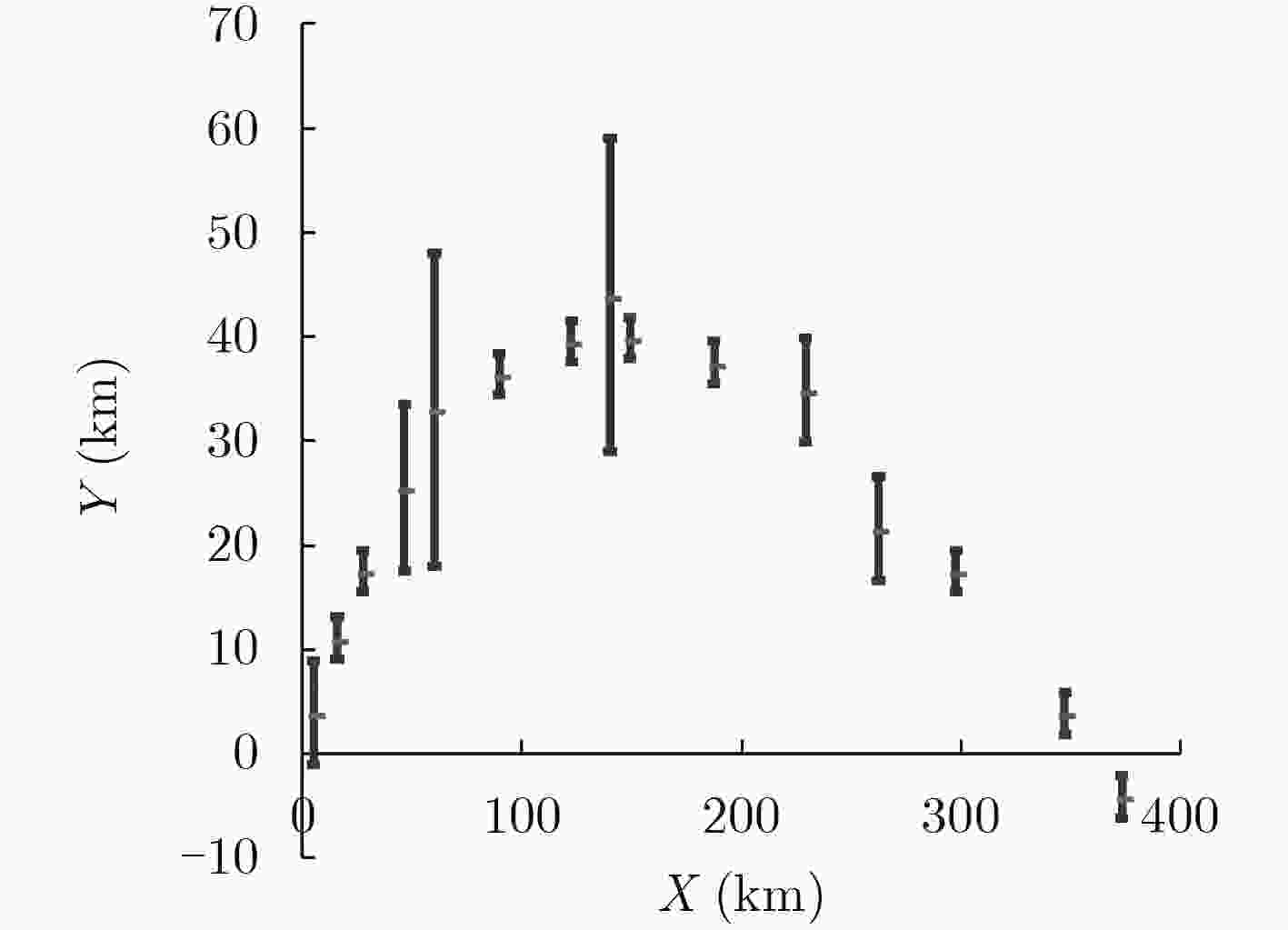
表 1 目标轨迹观测值

时刻(h)	X轴(km)	Y轴(km)
1	5.1	3.9
3	15.9	11.1
5	27.5	17.5
8	43.4	25.6
10	63.0	33.0
14	89.6	36.4
18	122.4	39.6
20	144.0	44.0
21	149.1	39.9
25	187.5	37.5
29	229.1	34.9
32	262.4	21.6
35	297.5	17.5
39	347.1	3.9
41	373.1	–4.1

下载: 导出CSV

参考文献(17)

孙辉, 赵峰, 张峰云. 多传感器信息融合技术及其应用[J]. 海洋测绘, 2009, 29(5): 77–81 doi: 10.3969/j.issn.1671-3044.2009.05.023

SUN Hui, ZHAO Feng, and ZHANG Fengyun. Multisensor information fusion technology and application[J]. Hydrographic Surveying and Charting, 2009, 29(5): 77–81 doi: 10.3969/j.issn.1671-3044.2009.05.023

姜楷娜. 基于卡尔曼滤波的目标轨迹跟踪仿真研究[J]. 中国科技信息, 2017(17): 105–106 doi: 10.3969/j.issn.1001-8972.2017.17.036

JIANG Kaina. Research on target tracking based on Kalman filter[J]. Chian Science and Technology Information, 2017(17): 105–106 doi: 10.3969/j.issn.1001-8972.2017.17.036

王雪君, 孙进平, 张旭旺. 基于压缩感知的PD雷达序贯扩展卡尔曼滤波跟踪方法[J]. 信号处理, 2017, 33(4): 601–606 doi: 10.16798/j.issn.1003-0530.2017.04.022

WANG Xuejun, SUN Jinping, and ZHANG Xuwang. Progressive Extended Kalman Filter Tracking Method Based on Compressive Sensing for PD Radar[J]. Journal of Signal Processing, 2017, 33(4): 601–606 doi: 10.16798/j.issn.1003-0530.2017.04.022

刘晨光, 程丹松, 刘家锋, 等. 一种基于交互式粒子滤波器的视频中多目标跟踪算法[J]. 电子学报, 2011, 39(2): 260–267

LIU Chenguang, CHENG Dansong, LIU Jiafeng, et al. A multi-target tracking algorithm in video based on interactive particle filter[J]. Acta Electronica Sinica, 2011, 39(2): 260–267

陈思静, 张可. VANETs中的车辆移动规律性及轨迹预测研究[J]. 计算机工程与应用, 2016, 52(18): 139–143 doi: 10.3778/j.issn.1002-8331.1410-0313

CHEN Sijing and ZHANG Ke. Research on vehicle movement regularity and trajectory prediction in VANETs[J]. Computer Engineering and Applications, 2016, 52(18): 139–143 doi: 10.3778/j.issn.1002-8331.1410-0313

郭晓军, 万龙, 刘峰. 基于扩展卡尔曼滤波的空间小目标跟踪算法[J]. 电光与控制, 2016, 23(4): 57–61 doi: 10.3969/j.issn.1671-637X.2016.04.012

GUO Xiaojun, WAN Long, and LIU Feng. An algorithm for small space target tracking based on extended Kalman filter[J]. Electronics Optics&Control, 2016, 23(4): 57–61 doi: 10.3969/j.issn.1671-637X.2016.04.012

GELB A and BOOKSX I. Applied optimal estimation[J]. Proceedings of the IEEE, 1974, 64(4): 574–575.

沈凯, 管雪元, 李文胜. 扩展卡尔曼滤波在组合导航中的应用[J]. 传感器与微系统, 2017, 36(8): 158–160 doi: 10.13873/J.1000-9787(2017)08-0158-03

SHEN Kai, GUAN Xueyuan, and LI Wensheng. Application of EKF in integrated navigation system[J]. Transducer and Microsystem Technologies, 2017, 36(8): 158–160 doi: 10.13873/J.1000-9787(2017)08-0158-03

程兰, 王志远, 陈杰, 等. 基于粒子滤波和滑动平均扩展卡尔曼滤波的多径估计算法[J]. 电子与信息学报, 2017, 39(3): 709–716 doi: 10.11999/JEIT160587

CHENG Lan, WANG Zhiyuan, CHEN Jie, et al. An improved multipath estimation algorithm using particle filter and sliding average extended Kalman filter[J]. Journal of Electronics&Information Technology, 2017, 39(3): 709–716 doi: 10.11999/JEIT160587

朱海东, 葛万成. 车联网中的异构网络融合机制研究[J]. 通信技术, 2017, 50(8): 1691–1695 doi: 10.3969/j.issn.1002-0802.2017.08.017

ZHU Haidong and GE Wancheng. Heterogeneous network fusion mechanism in vehicle networks[J]. Communications Technology, 2017, 50(8): 1691–1695 doi: 10.3969/j.issn.1002-0802.2017.08.017

EVENSEN G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research Oceans, 1994, 99(C5): 10143–10162 doi: 10.1029/94JC00572

VERLAAN M and HEEMINK A W. Nonlinearity in data assimilation applications: A practical method for analysis[J]. Monthly Weather Review, 2001, 129(6): 1578–1589 doi: 10.1175/1520-0493(2001)129

ZHANG Zequn, LI Heng, and ZHANG Dongxiao. Water flooding performance prediction by multi-layer capacitance-resistive models combined with the ensemble Kalman filter[J]. Journal of Petroleum Science&Engineering, 2015, 127(1): 1–19 doi: 10.1016/j.petrol.2015.01.020

ZHANG Zequn, LI Heng, and ZHANG Dongxiao. Reservoir characterization and production optimization using the ensemble-based optimization method and multi-layer capacitance-resistive models[J]. Journal of Petroleum Science&Engineering, 2017, 156: 633–653 doi: 10.1016/j.petrol.2017.06.020

LIU Di, MISHRA A K, and YU Zhongbo. Evaluating uncertainties in multi-layer soil moisture estimation with support vector machines and ensemble Kalman filtering[J]. Journal of Hydrology, 2016, 538(1): 243–255 doi: 10.1016/j.jhydrol.2016.04.021

CUI Bo and ZHANG Jiashu. The improved ensemble Kalman filter for multisensor target tracking[C]. IEEE International Symposium on Information Science and Engineering, Shanghai, China, 2008: 263–265.

PORNSARAYOUTH S, WONGSAISUWAN M, and YAMAKITA M. An improvement of ensemble Kalman filter for OOSM tracking[J]. IFAC Proceedings Volumes, 2011, 44(1): 12003–12008 doi: 10.3182/20110828-6-it-1002.03399

施引文献

资源附件(0)

访问统计