基于分段凿孔的极化码级联方案

曹阳; 张晗; 涂巧玲; 李小红; 彭小峰

doi:10.11999/JEIT171113

基于分段凿孔的极化码级联方案

doi: 10.11999/JEIT171113

曹阳^{1, 2},
张晗^1, ,,
涂巧玲¹,
李小红¹,
彭小峰¹

1.
重庆理工大学电气与电子工程学院重庆 400054
2.
电子科技大学物理电子学院成都 611731

基金项目: 国家自然科学基金(61205106)，中国博士后科学基金(2014M552329)，重庆市教委科学技术研究项目(KJ1500934, KJ120827)，重庆市科委社会事业与民生保障科技创新专项(cstc2017shmsA40019)

详细信息

作者简介:
曹阳：男，1977年生，教授，博士后，研究方向为自由空间光通信、信道编码等

张晗：男，1993年生，硕士生，研究方向为信道编码、自由空间光通信

涂巧玲：女，1963年生，教授，研究方向为信道编码、无线传感网络等

李小红：女，1996年生，硕士生，研究方向为自由空间光通信、信道编码

彭小峰：男，1979年生，硕士，讲师，研究方向为自由空间光通信、嵌入式系统等

通讯作者:
张晗 446252177@qq.com

中图分类号: TN911.22
计量
- 文章访问数: 2318
- HTML全文浏览量: 848
- PDF下载量: 57
- 被引次数: 25
出版历程
- 收稿日期: 2017-11-27
- 修回日期: 2018-04-18
- 网络出版日期: 2018-05-30
- 刊出日期: 2018-08-01

Concatenated Polar Codes Scheme Based on Segmented Puncturing

1.
School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China
2.
School of Physical Electronics, University of Electronic Science and Technology of China, Chengdu 611731, China

Funds: The National Natural Science Foundation of China (61205106), China Postdoctoral Science Foundation (2014M552329), The Science and Technology Project Affiliated to the Education Department of Chongqing Municipality (KJ1500934, KJ120827), Chongqing Municipal Science and Technology Commission’s Special Project (cstc2017shmsA40019)

摘要

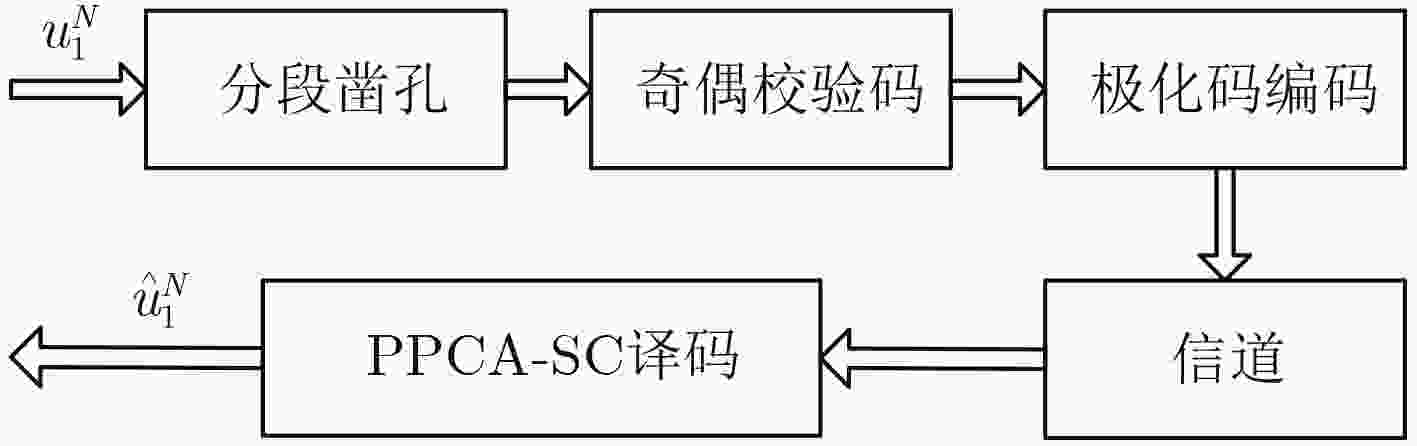
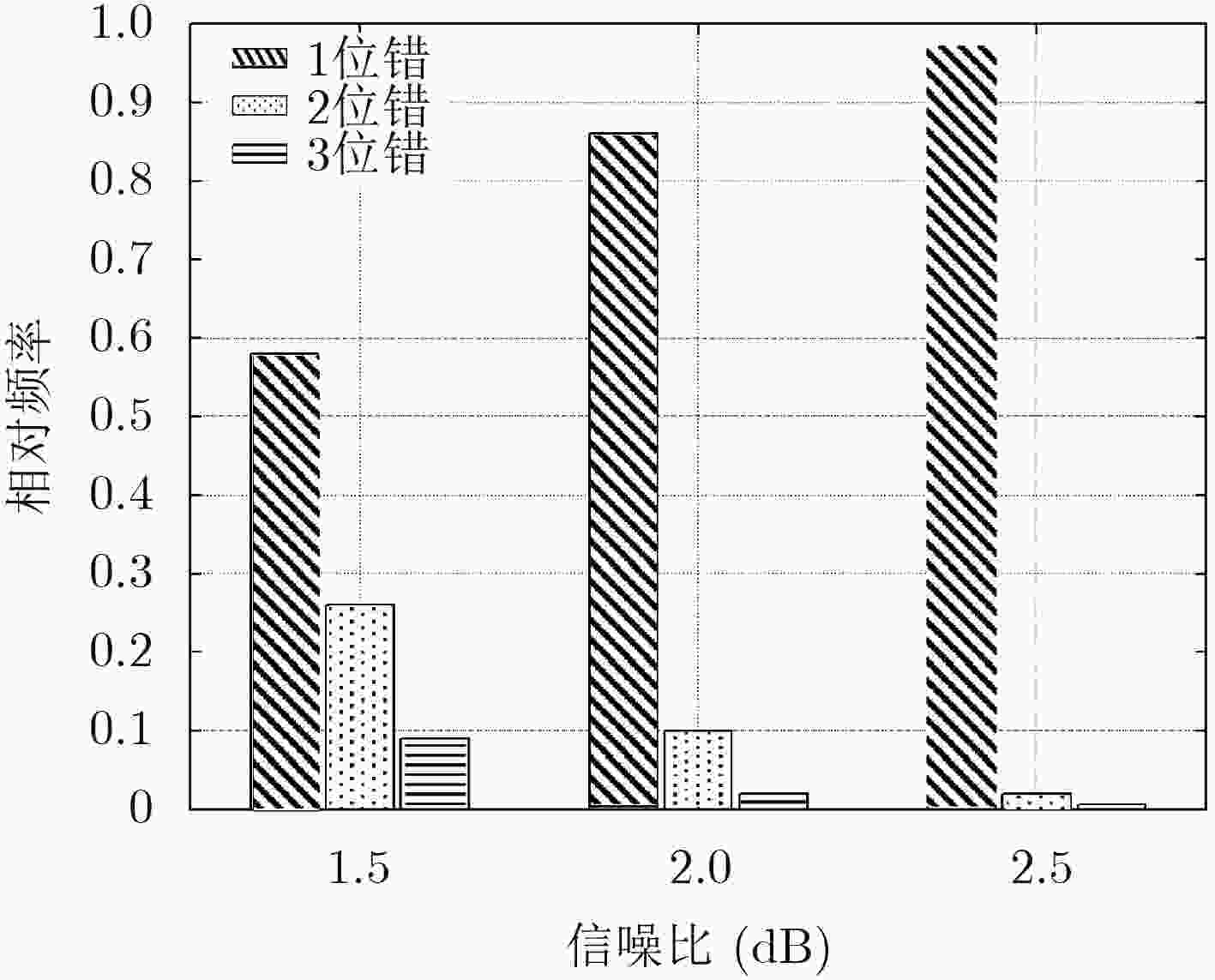
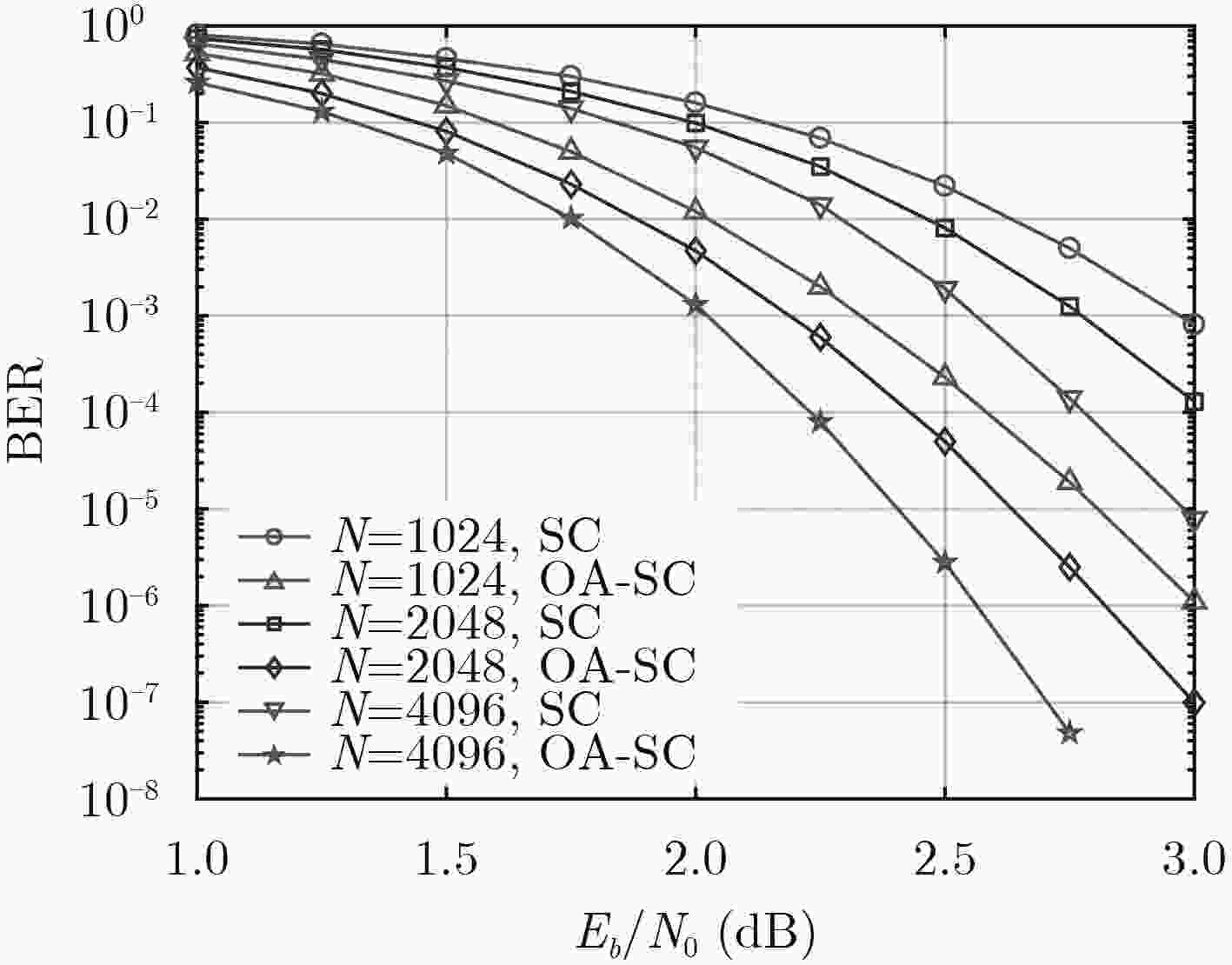
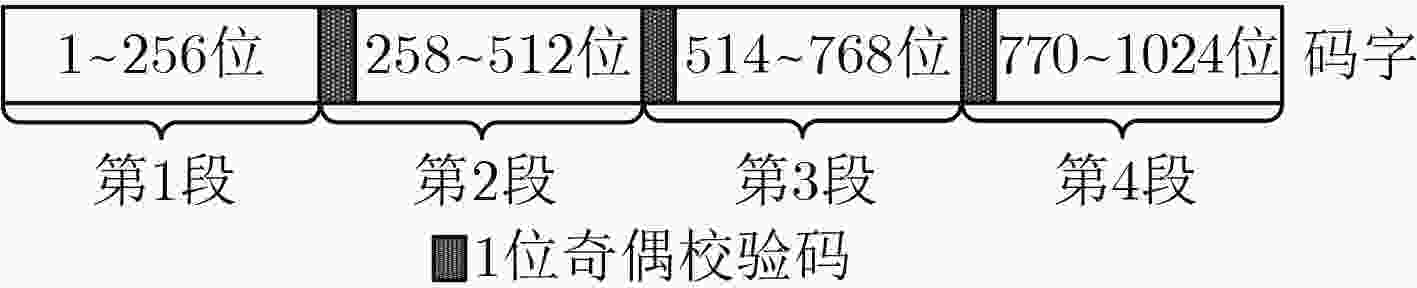
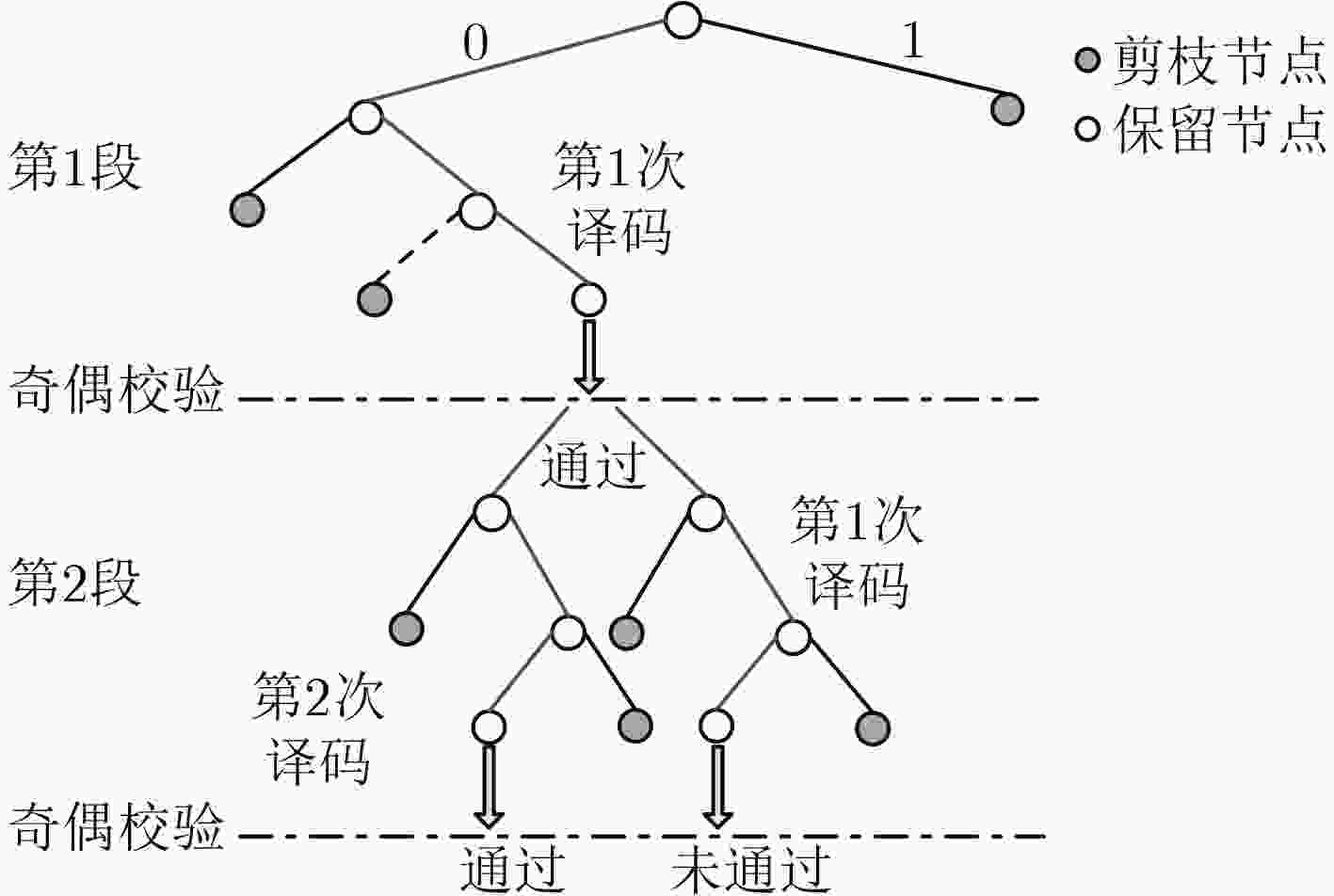
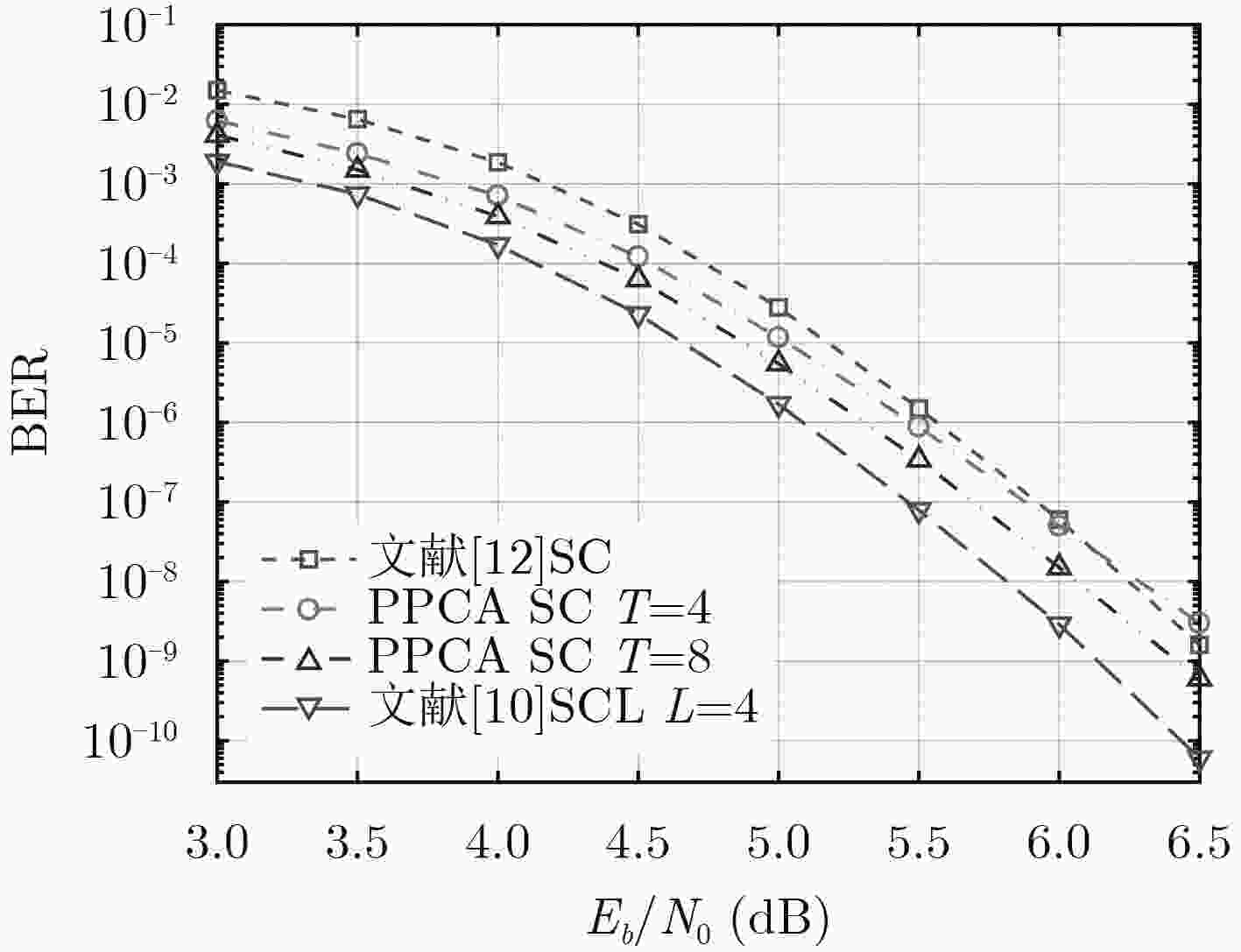
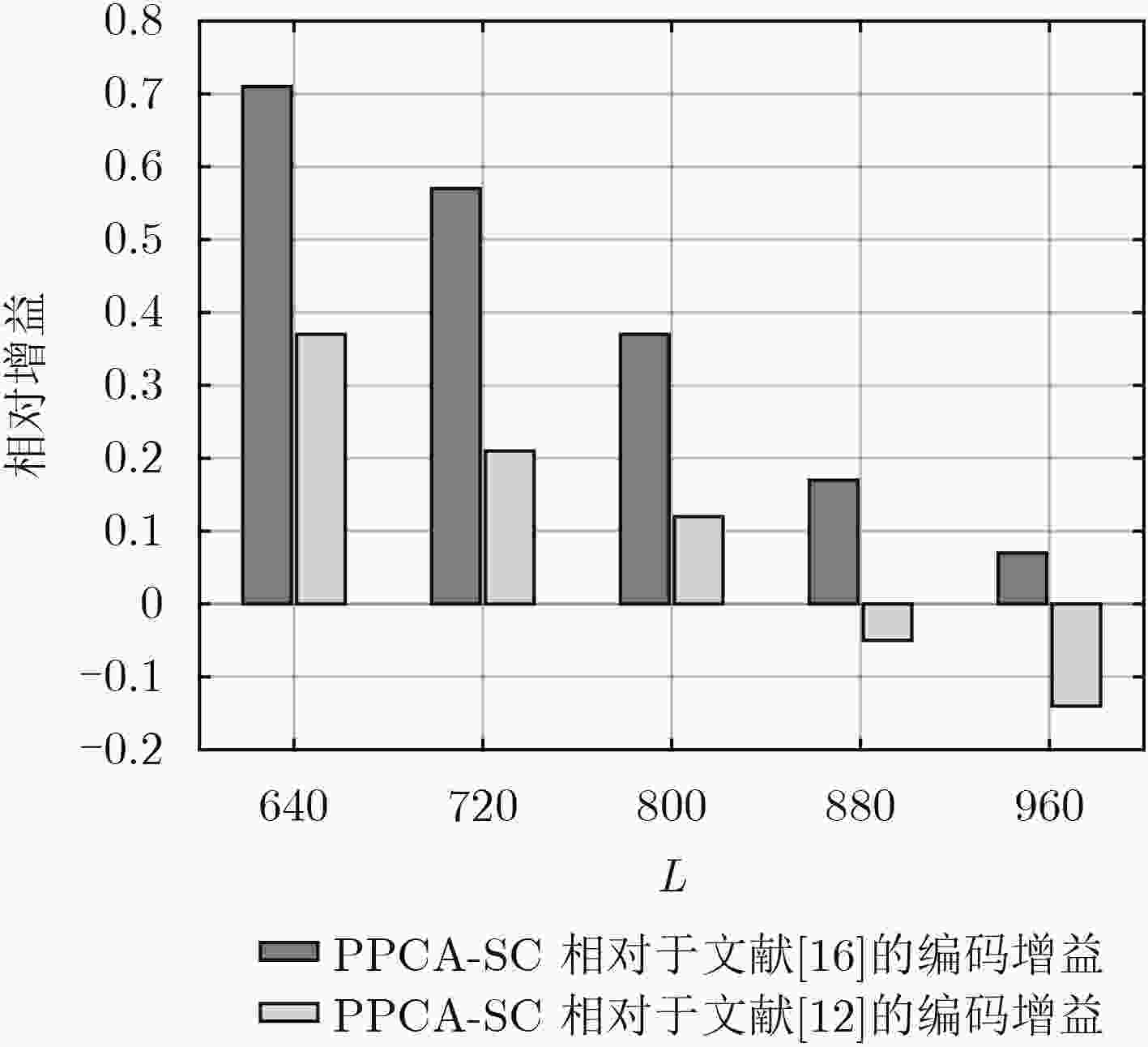
摘要: 极化码拥有出色的纠错性能，但编码方式决定了其码长不够灵活，需要通过凿孔构造码长可变的极化码。该文引入矩阵极化率来衡量凿孔对极化码性能的影响，选择矩阵极化率最大的码字作为最佳凿孔模式。对极化码的码字进行分段，有效减小了最佳凿孔模式的搜索运算量。由于各分段的第1个码字都会被凿除，且串行抵消译码过程中主要发生1位错，因此在各段段首级联奇偶校验码作为译码提前终止标志，检测前段码字的译码错误并进行重新译码。对所提方法在串行抵消译码下的性能进行仿真分析，结果表明，相比传统凿孔方法，所提方法在10^–3误码率时能获得约0.7 dB的编码增益，有效提升了凿孔极化码的译码性能。
- 极化码 /
- 串行抵消译码 /
- 凿孔 /
- 奇偶校验码 /
- 误码率
Abstract: Polar codes have outstanding error correction performance, but the code length of conventional polar codes is not compatible because of their coding method. To construct rate-compatible polar codes, a segmented puncturing method is proposed. Using the rate of polarization, the puncturing effect is measured and the codeword is removed to make the largest rate of polarization, which is the optimal puncturing mode. As the first codeword of the optimal puncturing mode is 0, the parity check codes are introduced to detect the decoding error of preceding segments codeword. The decoding performance of the method is simulated, results show that this method can obtain about 0.7 dB coding gain at 10^–3 bit error rate compared with the traditional puncturing method, which can effectively improve the performance of the punctured polar codes.
- Polar codes /
- Successive cancellation decoding /
- Puncturing /
- Parity check codes /
- Bit error rate

HTML全文

图 1 PPCA-SC编译码框图

下载: 全尺寸图片幻灯片

图 2 噪声引发的错误位数相对频率

下载: 全尺寸图片幻灯片

图 3 Oracle-Assisted SC与SC译码的误码率比较

下载: 全尺寸图片幻灯片

图 4 加入分段奇偶校验码示意图

下载: 全尺寸图片幻灯片

图 5 PPCA-SC译码过程

下载: 全尺寸图片幻灯片

图 6 不同凿孔方法的误码率比较

下载: 全尺寸图片幻灯片

图 7 不同译码方法的时间复杂度比较

下载: 全尺寸图片幻灯片

图 8 不同凿孔方法之间相对编码增益

下载: 全尺寸图片幻灯片

表 1 不同分段码长s 的译码性能增益比较

码长N	E_b/N₀(dB)
码长N	32	64	128	256	512	1024
s=4	0	0	0	0	0	0
s=8	0.012	0.036	0.091	0.108	0.138	0.159
s=16	–0.107	–0.043	0.055	0.118	0.188	0.233
最优s	8	8	8	16	16	16
对应m	4	8	16	16	32	64

下载: 导出CSV

表 2 剩余码长分配方法

算法1：剩余码长分配方法

输入：N, L,m, s

输出：

${L_1}$ ,

${L_2}$ ,

${n_1}$ ,

${n_2}$

(1) 定义

${L_1},\;{L_2}$ 为各分段中较短与较长的分段剩余码长；

(2) 定义

${n_{\min }},\;{n_{\max }}$ 为分段剩余码长为

${L_1},\;{L_2}$ 的分段个数；

(3) 较短分段剩余码长

${L_1} \!=\!\! \left\lfloor \!{\displaystyle\frac{{sL}}{N}}\! \right\rfloor$ ，较长分段剩余码长

${L_2} \! =\! \! \left\lceil \!{\displaystyle\frac{{sL}}{N}}\! \right\rceil$ ；

(4)

${n_1}$ 与

${n_2}$ 的比值为：

$\frac{{{n_1}}}{{{n_2}}} = \frac{{m{L_2} - L}}{{L - m{L_1}}}$ ；

(5)

${L_1}$ 的个数

${n_1} = \frac{{m{L_2}{\rm{ - }}L}}{{{L_2} - {L_1}}}$ ,

${L_{\max }}$ 的个数

${n_2} = \frac{{L{\rm{ - }}m{L_1}}}{{{L_2} - {L_1}}}$ 。

下载: 导出CSV

表 3 N=8对应的最佳凿孔模式

L	${{E} _{\max }}{\rm{(}}{{G}})$	${{{P}}_{8,L}}$
7	0.6008	01111111
6	0.6022	01111110
5	0.5949	00011111

下载: 导出CSV

表 4 N=16对应的最佳凿孔模式

L	${{E} _{\max }}{\rm{(}}{{G}})$	${{{P}}\!_{16,L}}$
15	0.5445	0111111111111111
14	0.5635	0111111111111110
13	0.5616	0111111111111100
12	0.5654	0111111111111000
11	0.5764	0111111011111000
10	0.5794	0111111011101000
9	0.5582	0111011011101000

下载: 导出CSV

表 5 PPCA-SC复杂度比较

信噪比(dB)	时间复杂度
1.5(PPCA-SC)	12275
2.0(PPCA-SC)	10858
2.5(PPCA-SC)	10360
SC	10240

下载: 导出CSV

表 6 PPCA-SC平均重复译码次数比较

码长	平均重复译码次数
256	0.72
512	0.47
1024	0.20

下载: 导出CSV

表 7 最大重复次数对PPCA-SC复杂度的影响

信噪比(dB)	最大重复次数	时间复杂度
1.5	4	3522
1.5	2	2527
2.0	4	2486
2.0	2	2331
2.5	4	2126
2.5	2	2107

下载: 导出CSV

表 8 分段数对PPCA-SC复杂度的影响

信噪比(dB)	分段数	时间复杂度
1.5	16	3522
1.5	8	3424
2.0	16	2466
2.0	8	2338
2.5	16	2126
2.5	8	2121

下载: 导出CSV

参考文献(17)

ARIKAN E and TELATAR E. On the rate of channel polarization[C]. 2009 IEEE International Symposium on Information Theory, Seoul, Korea, 2009: 1493–1495.

SASOGLU E, TELATAR E, and ARIKAN E. Polarization for arbitrary discrete memoryless channels[C]. IEEE Information Theory Workshop, Taormina, Italy, 2009: 144–148.

VANGALA H, HONG Y, and VITERBO E. Efficient algorithms for systematic polar encoding[J]. IEEE Communications Letters, 2016, 20(1): 17－20. DOI: 10.1109/LCOMM.2015.2497220.

TAHIR B and RUPP M. New construction and performance analysis of polar codes over AWGN channels[C]. 2017 24th International Conference on Telecommunications (ICT), Limassol, Cyprus, 2017: 1–4.

NIU Kai and CHEN Kai. CRC-aided decoding of polar codes[J]. IEEE Communications Letters, 2012, 16(10): 1668－1671. DOI: 10.1109/LCOMM.2012.090312.121501.

SHARMA A and SALIM M. Polar code: The channel code contender for 5G scenarios[C]. IEEE International Conference on Computer, Communications and Electronics, Jaipur, India, 2017: 676–682.

CHANDESRIS L, SAVIN V, and DECLERCQ D. On puncturing strategies for polar codes[C]. IEEE International Conference on Communications Workshops, Paris, France, 2017: 766–771.

BIOGLIO V, GABRY F, and LAND I. Low-complexity puncturing and shortening of polar codes[C]. Wireless Communications and Networking Conference Workshops, San Francisco, USA, 2017: 1–6.

ESLAMI A and PISHRO N. A practical approach to polar codes[C]. IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 2011: 16–20.

HONG S N, HUI D, and MARIĆ I. On the catastrophic puncturing patterns for finite-length polar codes[C]. Signals, Systems and Computers, 2016, Asilomar Conference, Pacific Grove, USA, 2017: 235–239.

NIU Kai, CHEN Kai, and LIN Jiaru. Beyond turbo codes: Rate-compatible punctured polar codes[C]. IEEE International Conference on Communications, Pacific Grove, USA, 2013: 3423–3427.

WANG Runxin and LIU Rongke. A novel puncturing scheme for polar codes[J]. IEEE Communications Letters, 2014, 18(12): 2081–2084. DOI: 10.1109/LCOMM.2014.2364845.

KORADA S B, ŞAŞOǦLU E, and URBANKE R. Polar codes: Characterization of exponent, bounds, and constructions[J]. IEEE Transactions on Information Theory, 2010, 56(12): 6253－6264. DOI: 10.1109/TIT.2010.2080990.

LEE M K and YANG K. The exponent of a polarizing matrix constructed from the Kronecker product[J]. Designs Codes & Cryptography, 2014, 70(3): 313－322. DOI: 10.1007/s10623-012-9689-z.

SHIN D M, LIM S C, and YANG K. Mapping selection and code construction for 2.m-ary polar-coded modulation[J]. IEEE Communications Letters, 2012, 16(6): 905－908. DOI: 10.1109/LCOMM.2012.040912.120070

SHIN D M, LIM S C, and YANG K. Design of Length-compatible polar codes based on the reduction of polarizing matrices[J]. IEEE Transactions on Communications, 2013, 61(7): 2593－2599. DOI: 10.1109/TCOMM.2013.052013.120543.

AFISIADIS O, BALATSOUKAS-STIMMING A, and BURG A. A low-complexity improved successive cancellation decoder for polar codes[C]. Signals, Systems and Computers, Asilomar Conference, Pacific Grove, USA, 2014: 2116–2120.

施引文献

期刊类型引用(14)

1.	赵锋，徐志明，刘蕾，艾小锋. 弹道目标特征提取研究现状与展望. 信息对抗技术. 2022(03): 15-32 . 百度学术
2.	徐志明，艾小锋，刘晓斌，吴其华，赵锋. 基于散射中心滑动特性的双基地雷达锥体目标微动特征提取方法. 电子学报. 2021(03): 461-469 . 百度学术
3.	汤华涛，察豪，刘峰. 考虑微多普勒特征的鸟类目标多假设跟踪算法. 舰船电子工程. 2020(05): 43-47 . 百度学术
4.	黄翔东，黎鸣诗，罗蓬，马欣. 基于全相位谱分析的多频内插迭代频率估计器. 振动与冲击. 2019(01): 89-95 . 百度学术
5.	魏嘉琪，张磊，刘宏伟，周叶剑. 基于相位测距的宽带雷达弹道目标微动几何参数估计. 电子与信息学报. 2018(09): 2227-2234 . 本站查看
6.	宋鑫华，叶春茂，杨健. 一种基于雷达窄带回波的转动参数估计方法. 太赫兹科学与电子信息学报. 2018(06): 1087-1092 . 百度学术
7.	李彦兵，张曦文，李飞，陈大庆，高红卫. 一种大加速度机动目标微动参数估计方法. 电子与信息学报. 2017(01): 82-87 . 本站查看
8.	周叶剑，张磊，菅毛，王虹现，邢孟道. 多频调频稀疏分解的微动目标参数估计方法. 电子与信息学报. 2017(10): 2360-2365 . 本站查看
9.	沈菲菲，李立钢，贾配洋，宋振健. 一种基于雷达微多普勒效应苍蝇识别的方法. 电子设计工程. 2017(09): 22-26+30 . 百度学术
10.	曹文杰，赵新燕. 基于三次样条插值的微动目标特征提取. 舰船电子对抗. 2017(04): 55-58 . 百度学术
11.	夏鹏，田西兰. 基于微多普勒信息的弹道目标成像. 雷达科学与技术. 2017(05): 553-557 . 百度学术
12.	肖金国，杜兰，韩勋，曹文杰，刘宏伟. 基于参数化时频分析的进动锥裙目标瞬时微多普勒频率提取方法. 电子与信息学报. 2016(01): 90-96 . 本站查看
13.	黄翔东，王越冬，靳旭康，吕卫. 无窗全相位FFT/FFT相位差频移补偿频率估计器. 电子与信息学报. 2016(05): 1135-1142 . 本站查看
14.	陈春晖，张群，罗迎，孙玉雪. 一种空间微动目标宽带雷达干涉三维成像方法. 电子与信息学报. 2016(12): 3144-3151 . 本站查看