Kernel Extreme Learning Machine Based on K Interpolation Simplex Method
-
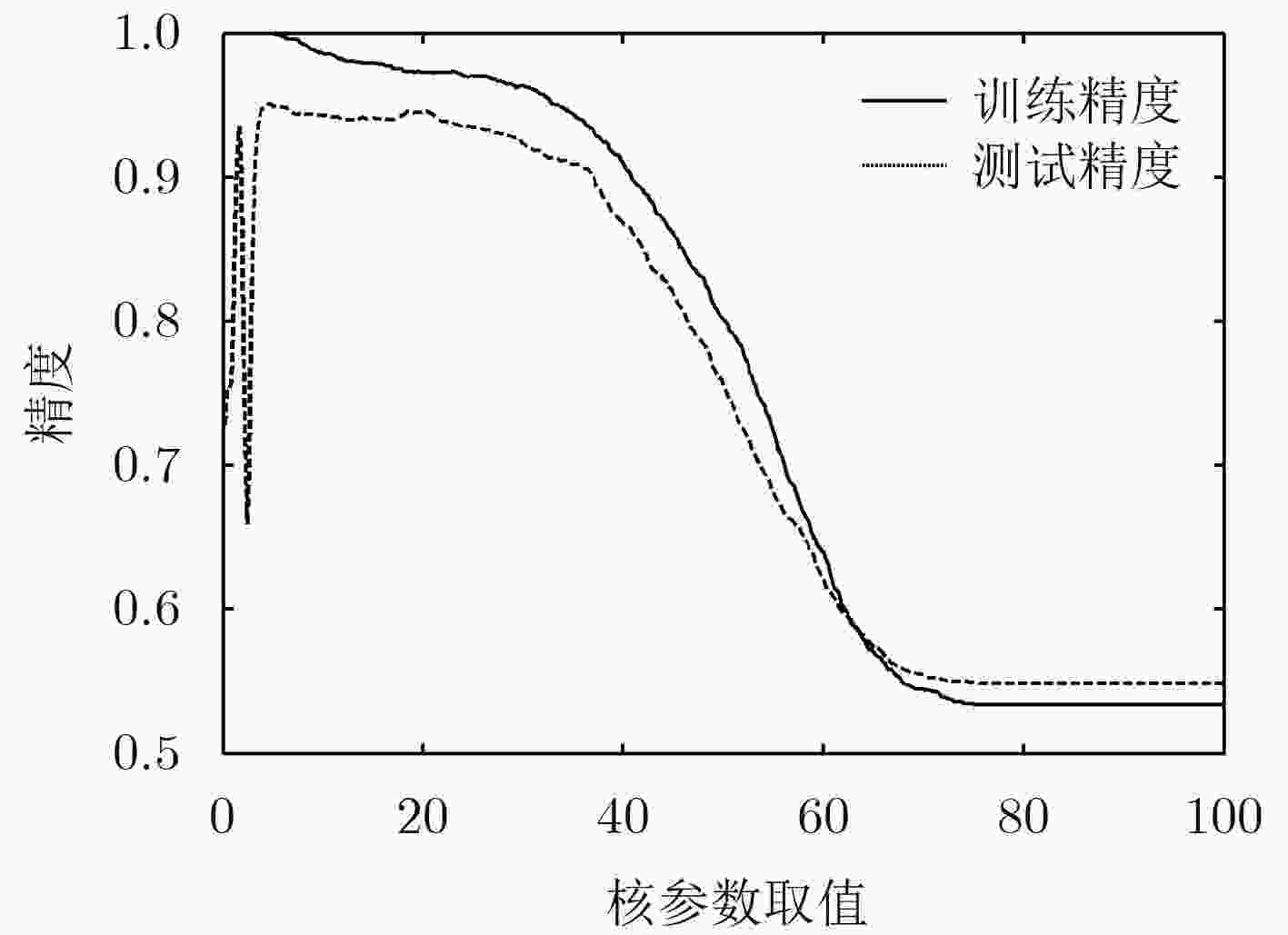
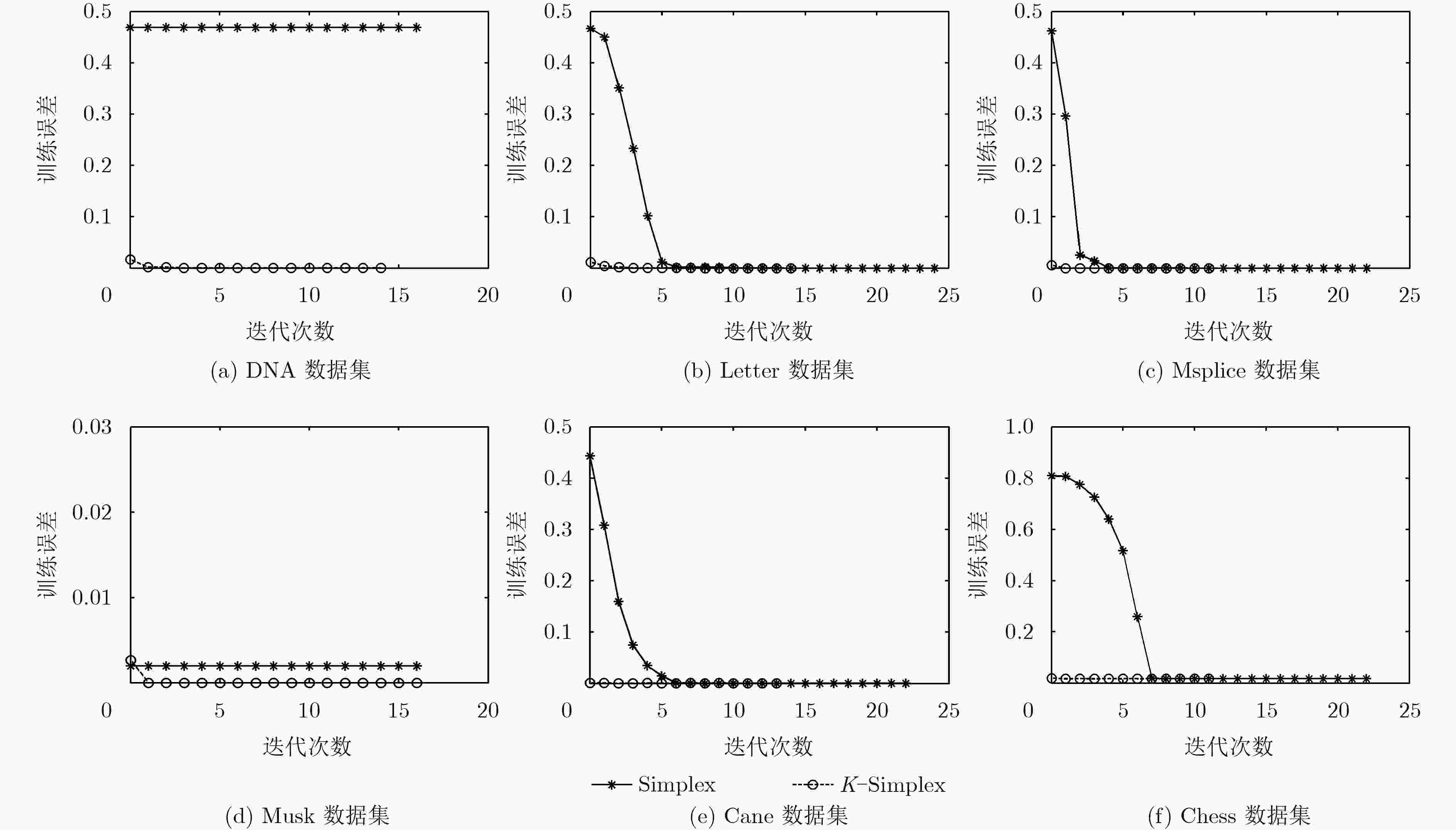
摘要: 针对核极限学习机高斯核函数参数选优难,影响学习机训练收敛速度和分类精度的问题,该文提出一种K插值单纯形法的核极限学习机算法。把核极限学习机的训练看作一个无约束优化问题,在训练迭代过程中,用Nelder-Mead单纯形法搜索高斯核函数的最优核参数,提高所提算法的分类精度。引入K插值为Nelder-Mead单纯形法提供合适的初值,减少单纯形法的迭代次数,提高了新算法的训练收敛效率。通过在UCI数据集上的仿真实验并与其它算法比较,新算法具有更快的收敛速度和更高的分类精度。
-
关键词:
- 核极限学习机 /
- 核参数 /
- Nelder-Mead单纯形法 /
- K插值法
Abstract: The kernel Extreme Learning Machine (ELM) has a problem that the kernel parameter of the Gauss kernel function is hard to be optimized. As a result, training speed and classification accuracy of kernel ELM are negatively affected. To deal with that problem, a novel kernel ELM based on K interpolation simplex method is proposed. The training process of kernel ELM is considered as an unconstrained optimal problem. Then, the Nelder-Mead Simplex Method (NMSM) is used as an optimal method to search the optimized kernel parameter, which improves the classification accuracy of kernel ELM. Furthermore, the K interpolation method is used to provide appropriate initial values for the Nelder-Mead simplex to reduce the number of iterations, and as a result, the training speed of ELM is improved. Comparative results on UCI dataset demonstrate that the novel ELM algorithm has better training speed and higher classification accuracy. -
表 1 1维单纯形子算法
输入:初始搜索点 \small${\delta _0}$,数据集X,目标函数的计算公式 \small$F(\delta )$,最大迭代次数MT,单纯形的最小半径SR。 输出:最优核参数 \small${\delta ^*}$。 步骤1 根据给定的初始化点 \small${\delta _0}$构造初始单纯形; 步骤2 对于1维单纯形的两个顶点A和B,计算出目标函数值 \small$F(\delta _{\rm A})$和 \small$F(\delta _{\rm B})$,函数值较小的为best点,较大的为worst点; 步骤3 计算反射点R和反射点处的目标函数值 \small$F(\delta _{\rm R})$,如果反射点的目标函数值优于best点,则进入步骤4;如果差于best点,则转步骤5;如 果反射点与best点处目标值相等,则转步骤6; 步骤4 计算扩展点E和扩展点处的目标函数值 \small$F(\delta _{\rm E})$,比较反射点R处和扩展点E的目标函数值,选择目标函数值较小的点替换单纯形中的 worst点,然后转步骤7; 步骤5 比较反射点R与worst点处的目标函数值,根据比较结果确定压缩点M的位置,若压缩点M的目标函数值 \small$F({\delta _M})$与worst点相比更小,则 用M点替换worst点,然后转步骤7;否则,转步骤6; 步骤6 执行单纯形收缩操作; 步骤7 若达到最大迭代次数MT,或单纯形半径小于SR,则迭代结束,best顶点对应的 \small$\delta $值即为最优核参数值 \small${\delta ^*}$;否则,转步骤2进行下一次 迭代。 表 2 K插值单纯形法核极限学习机训练算法
输入:训练数据集X,测试数据集Y。 输出:最优核参数 \small${\delta ^*}$、分类函数 \small$\tilde {{f}}(\cdot)$,测试数据集的分类结果。 步骤1 初始化参数,给定插值数目K,正则化参数C,最大迭代次数MT,单纯形最小半径SR; 步骤2 数据预处理; 步骤3 计算K个插值核参数在训练数据集X上的训练精度,并从中找到合适的初始搜索点 \small${\delta _0}$: (1)构造核参数 \small$\delta $的K个插值点 \small${\delta _i}$。 \small${\delta _i} = {2^{i - 1}}$,其中 \small$i = 1,2, ·\!·\!· ,K$; (2)用式(8)分别计算K个插值点 \small${\delta _i}$下相应的分类参数 \small${\tilde {β} _i}$,其中i=1,2,···,K; (3)用式(9)计算K个插值点 \small${\delta _i}$下的分类结果和训练精度 \small${P_{{\delta _i}}}$,其中i=1,2,···,K;
(4)构造训练精度矩阵 \small${S} = \left[ {\begin{array}{*{20}{c}} {{\delta _1}}&{{P_{{\delta _1}}}} \\ {{\delta _2}}&{{P_{{\delta _2}}}} \\ \vdots & \vdots \\ {{\delta _k}}&{{P_{\delta_k}}} \end{array}} \right]$;(5)删除训练精度矩阵 \small${S}$中 \small${P_{{\delta _i}}} \ge 0.999$的行,得到 \small${S}'$; (6)取 \small${S}'$矩阵中的 \small${S}'\left( {1,1} \right)$元素作为初始搜索点 \small${\delta _0}$; 步骤4 调用单纯形法优化核参数子算法,进行迭代搜索,传入搜索初值 \small${\delta _0}$,数据集X,目标函数计算公式 \small$F(\delta )$,最大迭代次数MT和单纯形 最小半径SR,得到最优核参数 \small${\delta ^*}$; 步骤5 根据最优核参数 \small${\delta ^*}$,用式(8)计算核ELM的分类参数 \small$\tilde {β} $; 步骤6 对于测试数据集Y中的待分类样本 \small${{x}_p}$,根据最优核参数和步骤5的 \small$\tilde{β} $,用式(9)计算 \small${{x}_p}$的类别。 表 3 实验数据集列表
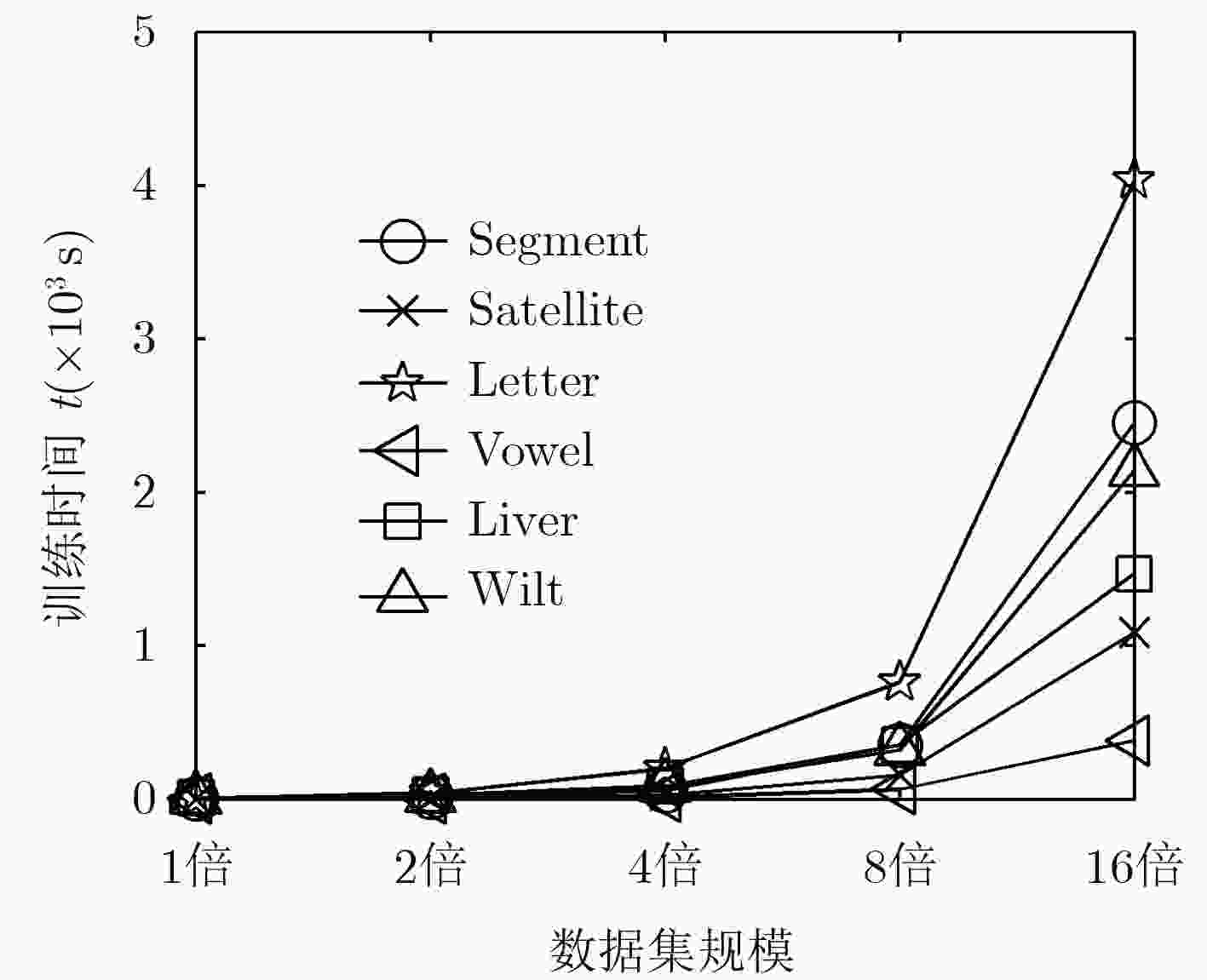
数据集 样本数目 属性数目 簇的数目 数据集 样本数目 属性数目 簇的数目 DNA 1967 180 3 Segment 2310 19 7 Letter 20000 16 26 Satellite 6435 36 6 Msplice 3044 240 3 Vowel 990 14 11 Musk 5692 166 2 Liver 345 7 2 Cnae 1080 857 9 Wilt 4839 5 2 Chess 28056 6 18 D31 3100 2 31 表 4 两种核极限学习机算法的分类精度比较
数据集 传统核ELM(%) KS-KELM \small$\delta $=0.01 \small$\delta $=0.1 \small$\delta $=1 \small$\delta $=10 \small$\delta $=50 \small$\delta $=100 最好精度 最差精度 平均精度 \small$\delta $值 精度(%) DNA 21.41 24.63 80.94 94.65 66.38 55.03 94.65 21.41 57.17 4.5 95.72 Letter 4.19 83.32 89.04 77.88 54.22 49.69 89.04 4.19 59.72 2.4521 96.92 Msplice 54.86 59.59 79.53 94.24 75.52 54.86 94.24 54.86 69.77 6 94.82 Musk 84.08 86.09 89.96 95.22 95.94 96.13 96.13 84.08 91.24 224 96.99 Cnae 9.27 80.39 91.38 88.58 71.55 49.35 91.38 9.27 65.09 1.6631 92.67 Chess 0.17 58.55 62.10 32.82 24.35 22.08 62.10 0.17 33.35 0.832 63.21 D31 89.33 95.67 96.67 92.33 23.50 16.33 96.67 16.33 68.97 1.7471 97.17 -
HUANG Guangbing, ZHU Qinyu, and SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1): 489–501.DOI: 10.1016/j.neucom.2005.12.126. SALCEDO S S, CASANOVA M C, PASTOR S A, et al. Daily global solar radiation prediction based on a hybrid coral reefs optimization – extreme learning machine approach[J]. Solar Energy, 2014, 105: 91–98.DOI: 10.1016/j.solener.2014.04.009. SONG Yuedong and ZHANG Jiaxiang. Discriminating preictal and interictal brain states in intracranial EEG by sample entropy and extreme learning machine[J]. Journal of Neuroscience Methods, 2016, 257: 45–54.DOI: 10.1016/j.jneumeth.2015.08.026. SURI M and PARMAR V. Exploiting intrinsic variability of filamentary resistive memory for extreme learning machine architectures[J]. IEEE Transactions on Nanotechnology, 2015, 14(6): 963–968.DOI: 10.1109/TNANO.2015.2441112. DING Shifei, ZHAO Han, ZHANG Yanan, et al. Extreme learning machine: Algorithm, theory and applications[J]. Artificial Intelligence Review, 2015, 44(1): 103–115.DOI: 10.1007/s10462-013-9405-z. HUANG Guangbing, ZHOU Hongming, DING Xiaojian, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man & Cybernetics Part B, 2012, 42(2): 513–529.DOI: 10.1109/TSMCB.2011.2168604. HUANG Guangbing, DING Xiaojian, and ZHOU Hongming. Optimization method based extreme learning machine for classification.[J]. Neurocomputing, 2010, 74(1): 155–163.DOI: 10.1016/j.neucom.2010.02.019. VAN G T, SUYKENS J A, LANCKRIET G, et al. Bayesian framework for least-squares support vector machine classifiers, gaussian processes, and kernel Fisher discriminant analysis[J]. Neural Computation, 2014, 14(5): 1115–1147.DOI: 10.1162/089976602753633411. ADANKON M M, CHERIEL M, and AYAT N F. Optimizing resources in model selection for support vector machines[J]. Pattern Recognition, 2007, 40(3): 953–963.DOI: 10.1016/j.patcog.2006.06.012. XU Yitian, PAN Xianli, ZHOU Zhijian, et al. Structural least square twin support vector machine for classification[J]. Applied Intelligence, 2015, 42(3): 527–536.DOI: 10.1007/s10489-014-0611-4. XIAO Yingchao, WANG Huangang, ZHANG Lin, et al. Two methods of selecting Gaussian kernel parameters for one-class SVM and their application to fault detection[J]. Knowledge-Based Systems, 2014, 59(2): 75–84.DOI: 10.1016/j.knosys.2014.01.020. XIAO Yingchao, WANG Huangang, and XU Weili. Parameter selection of gaussian kernel for one-class SVM.[J]. IEEE Transactions on Cybernetics, 2015, 45(5): 941–953.DOI: 10.1109/TCYB.2014.2340433. TIAN Meng and WANG Wenjian. An efficient Gaussian kernel optimization based on centered kernel polarization criterion[J]. Information Sciences, 2015, 322: 133–149.DOI: 10.1016/j.ins.2015.06.010. LAGARIAS J C, WRIGHT M H, WRIGHT P E, et al. Convergence properties of the Nelder-Mead simplex method in low dimensions[J]. SIAM Journal on Optimization, 1998, 9(1): 112–147.DOI: 10.1137/S1052623496303470. 冯增喜, 任庆昌, 彭彦平, 等. 基于单纯形法的MFAC参数寻优[J]. 控制工程, 2016, 23(3): 405–410.DOI: 10.14107/j.cnki.kzgc.150456.FENG Zengxi, REN Qingchang, PENG Yanping, et al. Optimizing the parameters of MFAC based on the simplex method[J]. Control Engineering of China, 2016, 23(3): 405–410.DOI: 10.14107/j.cnki.kzgc.150456. 郑伟博, 张纪会. 基于Nelder-Mead单纯形法的改进量子行为粒子群算法[J]. 复杂系统与复杂性科学, 2016, 13(2): 97–104.DOI: 10.13306/j.1672-3813.2016.02.012.ZHENG Weibo and ZHANG Jihui. A improved quantum behaved particle swarm optimization algorithm using nelder and mead’s simplex algorithm[J]. Complex Systems & Complexity Science, 2016, 13(2): 97–104.DOI: 10.13306/j.1672-3813.2016.02.012. KEERTHI S S and LIN C J. Asymptotic behaviors of support vector machines with gaussian kernel[J]. Neural Computation, 2003, 15(7): 1667–1689.DOI: 10.1162/089976603321891855. 张小云, 刘允才. 高斯核支撑向量机的性能分析[J]计算机工程, 2003, 29(8): 22–25.DOI: 10.3969/j.issn.1000-3428.2003.08.009.ZHANG Xiaoyun and LIU Yuncai. Performance analysis of support vector machines with Gauss kernel[J]. Computer Engineering, 2003, 29(8): 22–25.DOI: 10.3969/j.issn.1000-3428.2003.08.009. 罗家祥, 罗丹, 胡跃明. 带权重变化和决策融合的ELM在线故障检测[J]. 控制与决策, 2017.DOI: 10.13195/j.kzyjc.2017.0274.该文献为网络优先出版, 暂时没有期卷号和页码LUO Jiaxiang, LUO Dan, and HU Yueming. A new online extreme learning machine with varying weights and decision level fusion for fault detection[J]. Control and Decision, 2017.DOI: 10.13195/j.kzyjc.2017.0274. ZHANG Yongshan, WU Jia, CAI Zhihua, et al. Memetic extreme learning machine[J]. Pattern Recognition, 2016, 58: 135–148.doi: 10.1016/j.patcog.2016.04.003. ZHANG Yongshan, WU Jia, Zhou Chuan, et al. Instance cloned extreme learning machine[J]. Pattern Recognition, 2017, 68: 52–65.DOI: 10.1016/j.patcog.2017.02.036. TANG Jiexiong, DENG Chenwei, and HUANG Guangbing. Extreme learning machine for multilayer perceptron[J]. IEEE Transactions on Neural Networks & Learning Systems, 2016, 27(4): 809–821.DOI: 10.1109/TNNLS.2015.2424995. -





 下载:
下载:


 下载:
下载:
