Fuzzy Clustering Ensemble Model Based on Distance Decision
-
摘要: 模糊聚类是近年来使用的一类性能较为优越的聚类算法,但该类算法对初始聚类中心敏感且对边界样本的聚类结果不够准确。为了提高聚类准确性、稳定性,该文通过联合多个模糊聚类结果,提出一种距离决策下的模糊聚类集成模型。首先,利用模糊C均值(FCM)算法对数据样本进行多次聚类,得到相应的隶属度矩阵。然后,提出一种新的距离决策方法,充分利用得到的隶属度关系构建一个累积距离矩阵。最后,将距离矩阵引入密度峰值(DP)算法中,利用改进的DP算法进行聚类集成以获取最终聚类结果。在UCI机器学习库中选择9个数据集进行测试,实验结果表明,相比经典的聚类集成模型,该文提出的聚类集成模型效果更佳。Abstract: Fuzzy clustering is a kind of clustering algorithm which shows superior performance in recent years, however, the algorithm is sensitive to the initial cluster center and can not obtain accurate results of clustering for the boundary samples. In order to improve the accuracy and stability of clustering, this paper proposes a novel approach of fuzzy clustering ensemble model based on distance decision by combining multiple fuzzy clustering results. First of all, performing several times clustering for data samples by using FCM (Fuzzy C-Means), and corresponding membership matrices are obtained. Then, a new method of distance decision is proposed, a cumulative distance matrix is constructed by the membership matrices. Finally, the distance matrix is introduced into the Density Peaks (DP) algorithm, and the final results of clustering are obtained by using the improved DP algorithm for clustering ensemble. The results of the experiment show that the clustering ensemble model proposed in this paper is more effective than other classical clustering ensemble model on the 9 data sets in UCI machine learning database.
-
表 1 算法实现流程
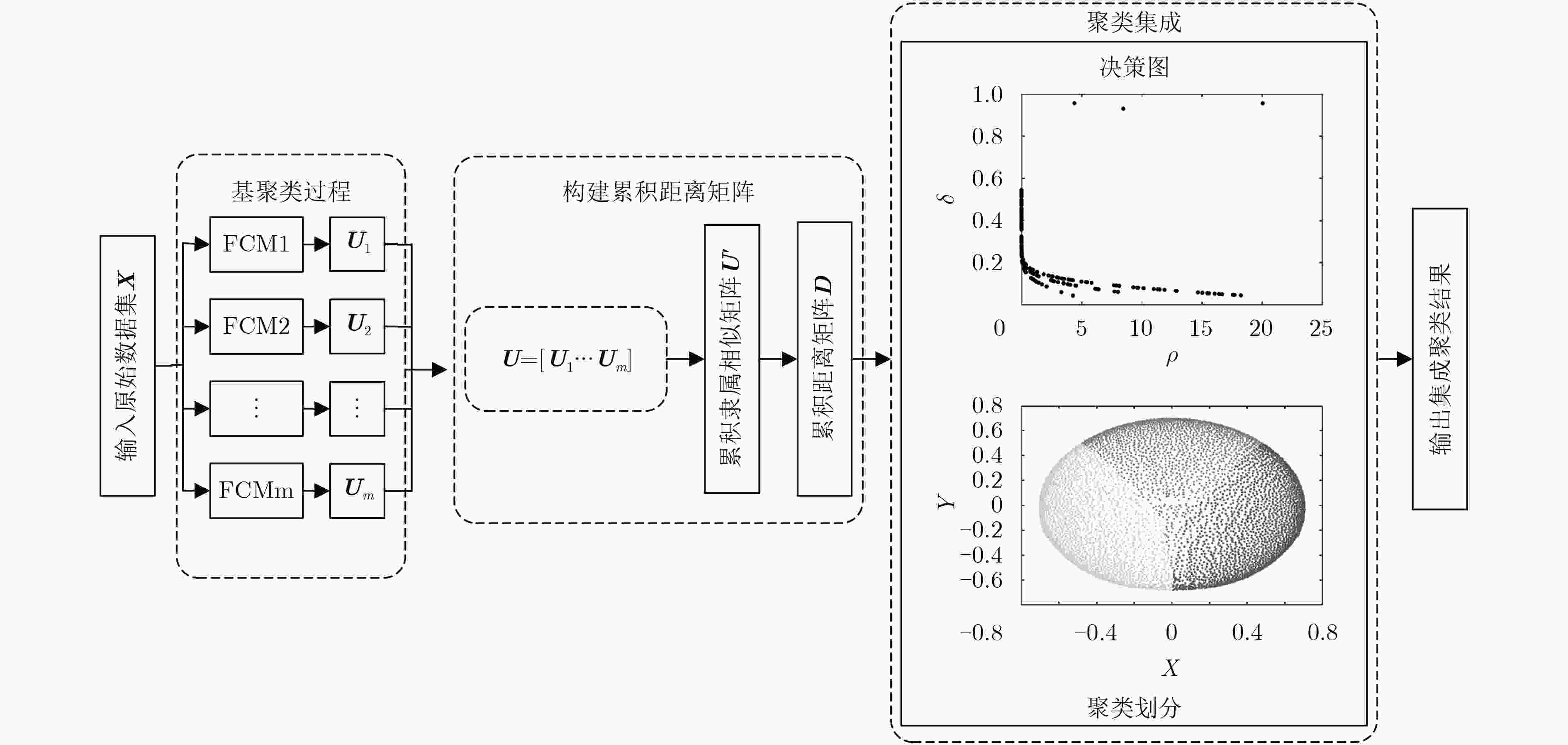
输入:实验数据集 $\small {{X}}{\rm{ = \{ }}{{x}_{i}}{\rm{|}}{i}{\rm{ = }}{1,2,}·\!·\!·\!{,}{n}{\rm{\} }}$,基聚类器运算次数 $\small {m}$,实验数据集的总类簇数 $\small C$ 输出:数据集 $\small {{X}}{\rm{ = \{ }}{{x}_{i}}{\rm{|}}{i}{\rm{ = }}{1,2,}·\!·\!·{,}{n}{\rm{\} }}$的聚类集成标签Q 步骤 1 获取基聚类FCM的聚类结果: (1) 判断基聚类器运算次数是否小于 $\small {m}$; (2) 利用范围在(0,1)之间的随机数初始化模糊隶属度 $\small {{{U}}_{j}},\;{j} = {1,2,}·\!·\!·\!{,}{m}$,满足式(1)的约束条件; (3) 通过式(2)计算 $\small C$个类簇的中心 $\small {c}_{k}^{j}{(}{k} = {1,2,}·\!·\!·\!{,}{C})$; (4) 通过式(1)计算FCM的目标函数,若 $\small {J_{hj}}(u,c)$小于设定阈值,或相对上次计算的目标函数的变化量 $\small \Delta {J_{hj}}$小于阈值,则迭代终止; (5) 利用式(3)重新计算新的模糊隶属度 $\small {{{U}}_j}$,返回(3); (6) 保存模糊隶属度 $\small {{U}_j}$, $\small j = j + 1$,返回(1); 步骤 2 构建累积距离矩阵: (1) 利用式(8)计算每次得到的隶属度矩阵 $\small {{{U}}_j},\ j = 1,2,·\!·\!·\!,m$对应的最大隶属类信息矩阵 $\small {{{L}}_j}$; (2) 利用式(9)计算单个隶属度矩阵 $\small {{{U}}_{j}}$与信息矩阵 $\small {{{L}}_j}$构造出的隶属相似矩阵 $\small {{{U}}\!_j}\!^\prime $为例进行距离矩阵的构建; (3) 重复执行 $\small {m}$次(2),得到累积隶属相似矩阵 $\small {{{U}}^\prime }$; (4) 利用式(10)构建累积距离矩阵 $\small {{D}}$; 步骤 3 基于DP的聚类集成: (1) 利用步骤2得到的累积距离矩阵 $\small {{D}}$计算数据样本间的两两距离 $\small {d_{ij}}$,并确定截断距离 $\small {d_c}$; (2) 按照式(4)和式(5)分别计算数据样本 $\small {x_i}$的局部密度 $\small {\rho _i}$和与更高局部密度的点的距离 $\small {\delta _i}$; (3) 利用式(11)中的 $\small {\gamma _i}$选择前K个密度峰值点作为集成聚类中心 $\small \{ {{c}_{k}}{,}{k} = {1,2,}·\!·\!·\!{,}{C}\} $,对非数据中心的数据样本进行归类; (4) 计算聚类的边界区域,排除光晕点的干扰。 表 2 实验数据集信息
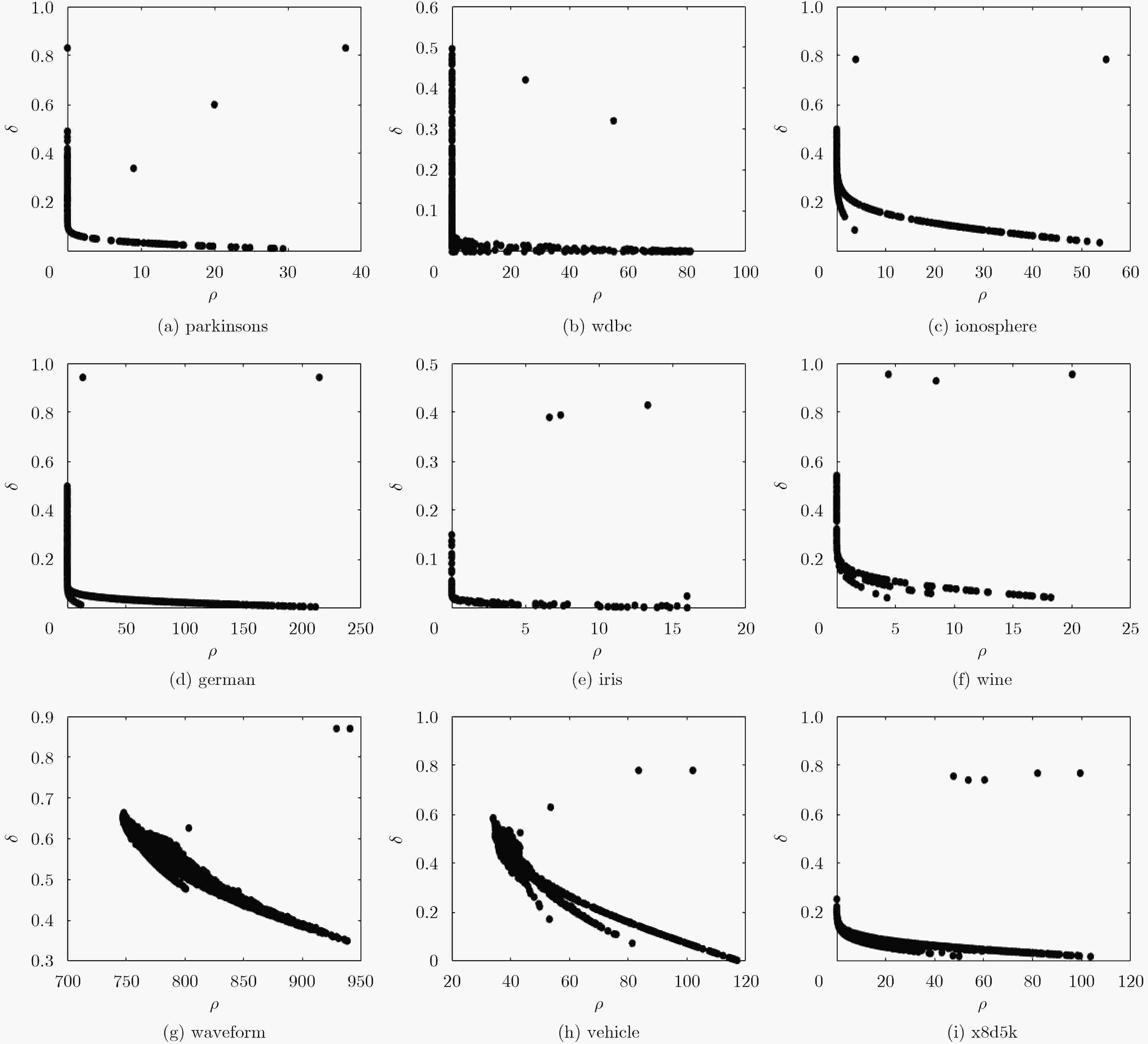
序号 1 2 3 4 5 6 7 8 9 数据集 parkinsons wdbc ionosphere german iris wine waveform vehicle x8d5k 数据样本数 195 569 351 1000 150 178 5000 846 1000 属性 22 30 34 24 4 13 21 18 8 类别数 2 2 2 2 3 3 3 4 5 表 3 5种聚类方法的RI比较结果
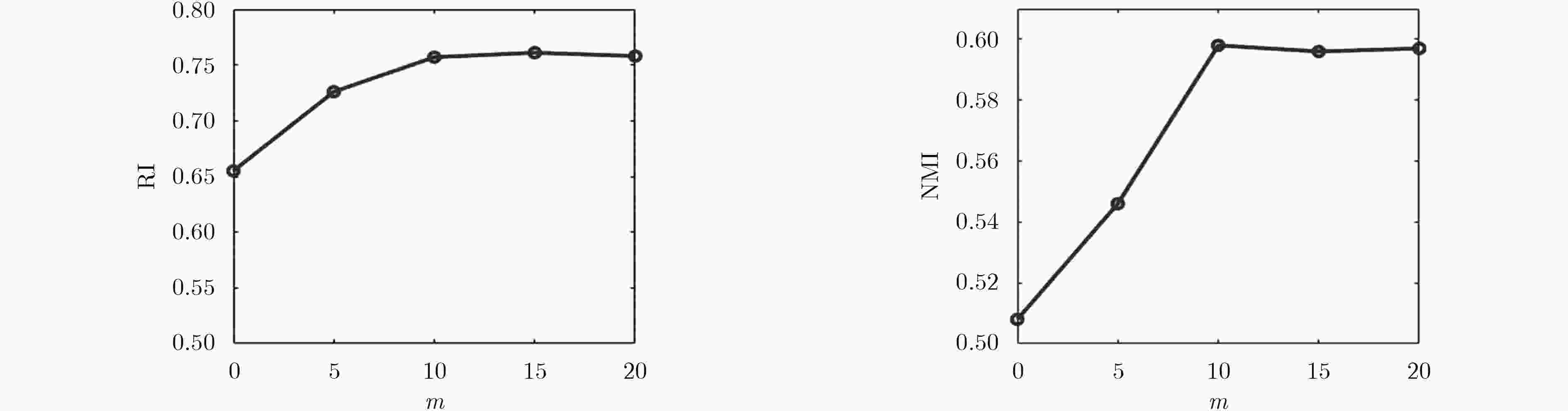
序号 FCM CSP HGP MCL 本文 均值 标准差 均值 标准差 均值 标准差 均值 标准差 均值 标准差 1 0.579 0.068 0.638 0.012 0.607 0.007 0.613 0.016 0.646 0.003 2 0.723 0.047 0.833 0.013 0.812 0.019 0.841 0.021 0.852 0.010 3 0.563 0.057 0.628 0.015 0.617 0.017 0.613 0.007 0.662 0.014 4 0.625 0.039 0.729 0.016 0.746 0.006 0.731 0.004 0.758 0.009 5 0.786 0.034 0.832 0.023 0.822 0.015 0.852 0.016 0.887 0.006 6 0.732 0.041 0.856 0.011 0.859 0.017 0.826 0.008 0.863 0.013 7 0.628 0.037 0.646 0.007 0.638 0.014 0.637 0.011 0.641 0.015 8 0.547 0.022 0.627 0.021 0.593 0.014 0.616 0.005 0.635 0.007 9 0.715 0.033 0.816 0.004 0.849 0.005 0.834 0.010 0.866 0.008 平均值 0.655 0.042 0.734 0.014 0.727 0.013 0.729 0.011 0.757 0.009 表 4 5种聚类方法的NMI比较结果
序号 FCM CSP HGP MCL 本文 均值 标准差 均值 标准差 均值 标准差 均值 标准差 均值 标准差 1 0.412 0.043 0.483 0.004 0.488 0.007 0.474 0.006 0.516 0.002 2 0.536 0.028 0.576 0.008 0.619 0.007 0.577 0.012 0.634 0.016 3 0.512 0.063 0.568 0.006 0.567 0.003 0.544 0.008 0.574 0.002 4 0.499 0.052 0.582 0.011 0.612 0.005 0.594 0.008 0.625 0.004 5 0.692 0.025 0.783 0.016 0.808 0.015 0.747 0.012 0.813 0.014 6 0.645 0.026 0.721 0.007 0.736 0.004 0.712 0.009 0.742 0.003 7 0.525 0.020 0.585 0.011 0.564 0.007 0.579 0.002 0.591 0.004 8 0.118 0.016 0.135 0.004 0.136 0.002 0.133 0.005 0.142 0.006 9 0.632 0.034 0.724 0.012 0.716 0.011 0.712 0.008 0.742 0.010 平均值 0.508 0.034 0.573 0.009 0.583 0.007 0.564 0.008 0.598 0.007 -
MEI Jianping, WANG Yangtao, CHEN Lihui, et al.. Large scale document categorization with fuzzy clustering[J]. IEEE Transactions on Fuzzy Systems, 2017, 25(5): 1239–1251. DOI: 10.1109/TFUZZ.2016.2604009. 张洁玉, 李佐勇. 基于核空间的加权邻域约束直觉模糊聚类算法[J]. 电子与信息学报, 2017, 39(9): 2162–2168. DOI: 10.11999/JEIT161317.ZHANG Jieyu and LI Zuoyong. Kernel-based algorithm with weighted spatial information intuitionistic fuzzy c-means[J]. Journal of Electronics & Information Technology, 2017, 39(9): 2162–2168. DOI: 10.11999/JEIT161317. 叶茂, 刘文芬. 基于快速地标采样的大规模谱聚类算法[J]. 电子与信息学报, 2017, 39(2): 278–284. DOI: 10.11999/JEIT160260.YE Mao and LIU Wenfen. Large scale spectral clustering based on fast landmark sampling[J]. Journal of Electronics & Information Technology, 2017, 39(2): 278–284. DOI: 10.11999/JEIT160260. 周林, 平西建, 徐森, 等. 基于谱聚类的聚类集成算法[J]. 自动化学报, 2012, 38(8): 1335–1342. DOI: 10.3724/SP.J.1004.2012.01335.ZHOU Lin, PING Xijian, XU Sen, et al.. Cluster ensemble based on spectral clustering[J]. Acta Automatica Sinica, 2012, 38(8): 1335–1342. DOI: 10.3724/SP.J.1004.2012.01335. 张敏, 于剑. 基于划分的模糊聚类算法[J]. 软件学报, 2004, 15(6): 858–868. DOI: 10.13328/j.cnki.jos.2004.06.008.ZHANG Min and YU Jian. Fuzzy partitional clustering algorithms[J]. Journal of Software, 2004, 15(6): 858–868. DOI: 10.13328/j.cnki.jos.2004.06.008. BEZDEK J C, HATHAWAY R J, SABIN M J, et al.. Convergence theory for fuzzy c-means: Counter-examples and repairs[J]. IEEE Transaction on Systems, Man, and Cybernetics, 1987, 17(5): 873–877. DOI: 10.1109/TSMC.1987.6499296. STREHL A and GHOSH J. Cluster ensembles a knowledge reuse framework for combining multiple partitions[J]. The Journal of Machine Learning Research, 2003, 3(3): 583–617. DOI: 10.1162/153244303321897735. GOSWAMI J P and MAHANTA A K. A genetic algorithm based ensemble approach for categorical data clustering[C]. Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 2015: 1–6. BANERJEE B, BOVOLO F, BHATTACHARYA A, et al.. A new self-training-based unsupervised satellite image classification technique using cluster ensemble strategy[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 741–745. DOI: 10.1109/LGRS.2014.2360833. HAO Zhifeng, WANG Lijuan, CAI Ruichu, et al.. An improved clustering ensemble method based link analysis[J]. World Wide Web, 2015, 18(2): 185–195. DOI: 10.1007/s11280-013-0208-6. ZHONG Caiming, YUE Xiaodong, ZHANG Zehua, et al.. A clustering ensemble: two-level-refined co-association matrix with path-based transformation[J]. Pattern Recognition, 2015, 48(8): 2699–2709. DOI: 10.1016/j.patcog.2015.02.014. 褚睿鸿, 王红军, 杨燕, 等. 基于密度峰值的聚类集成[J]. 自动化学报, 2016, 42(9): 1401–1412. DOI: 10.16383/j.aas.2016.c150864.CHU Ruihong, WANG Hongjun, YANG Yan, et al.. Clustering ensemble based on density peaks[J]. Acta Automatica Sinica, 2016, 42(9): 1401–1412. DOI: 10.16383/j.aas.2016.c150864. RODRIGUEZ A and LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492–1496. DOI: 10.1126/science.1242072. ZHOU Zhihua and TANG Wei. Clusterer ensemble[J]. Knowledge-Based Systems, 2006, 19(1): 77–83. DOI: 10.1016/j.knosys.2005.11.003. GAN Guojun, YANG Zijiang, and WU Jianhong. A genetic K-modes algorithm for clustering categorical data[J]. Springer Berlin Heidelberg, 2005, 36(2): 728–728. DOI: 10.1007/11527503_23. -





 下载:
下载:


 下载:
下载:
