Fast Two-dimensional DOA Estimation for Coherently Distributed Noncircular Signals with Automatic Pairing
-
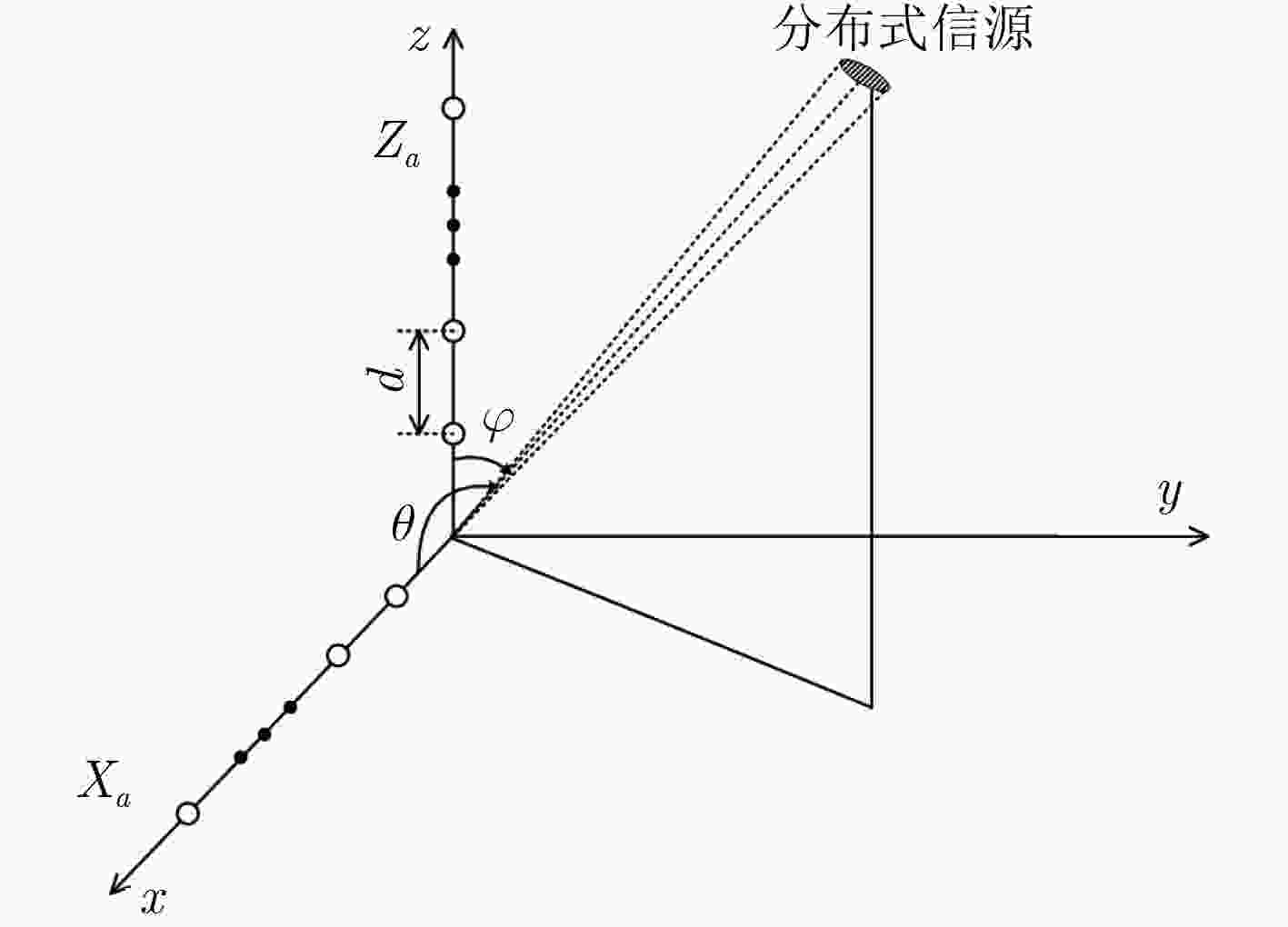
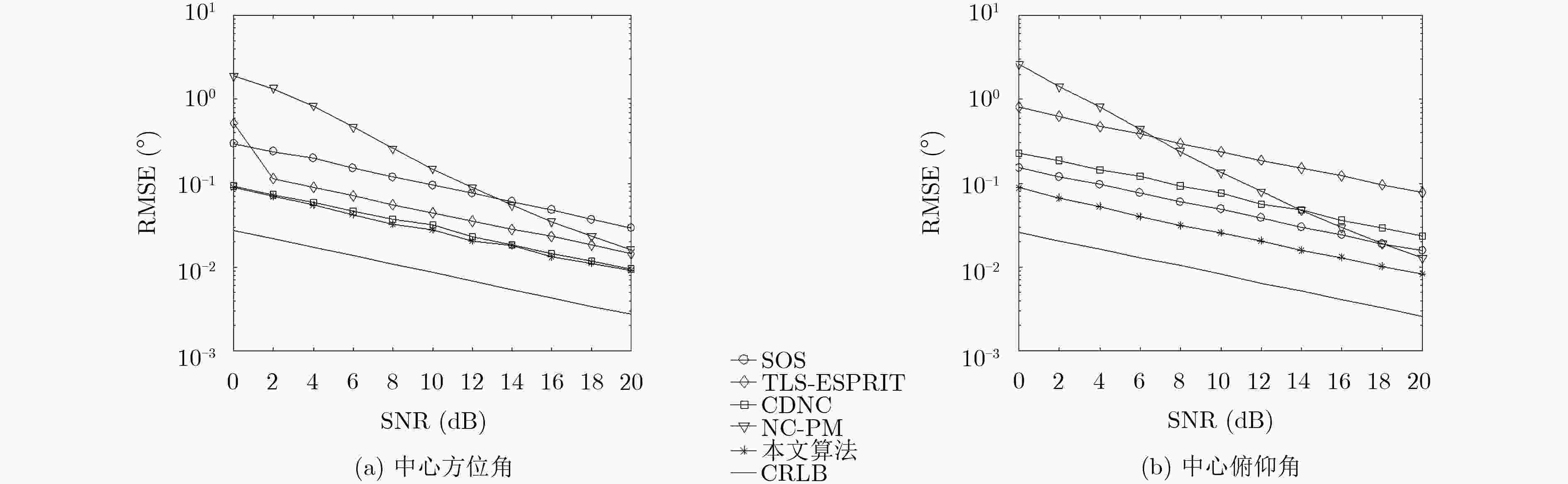
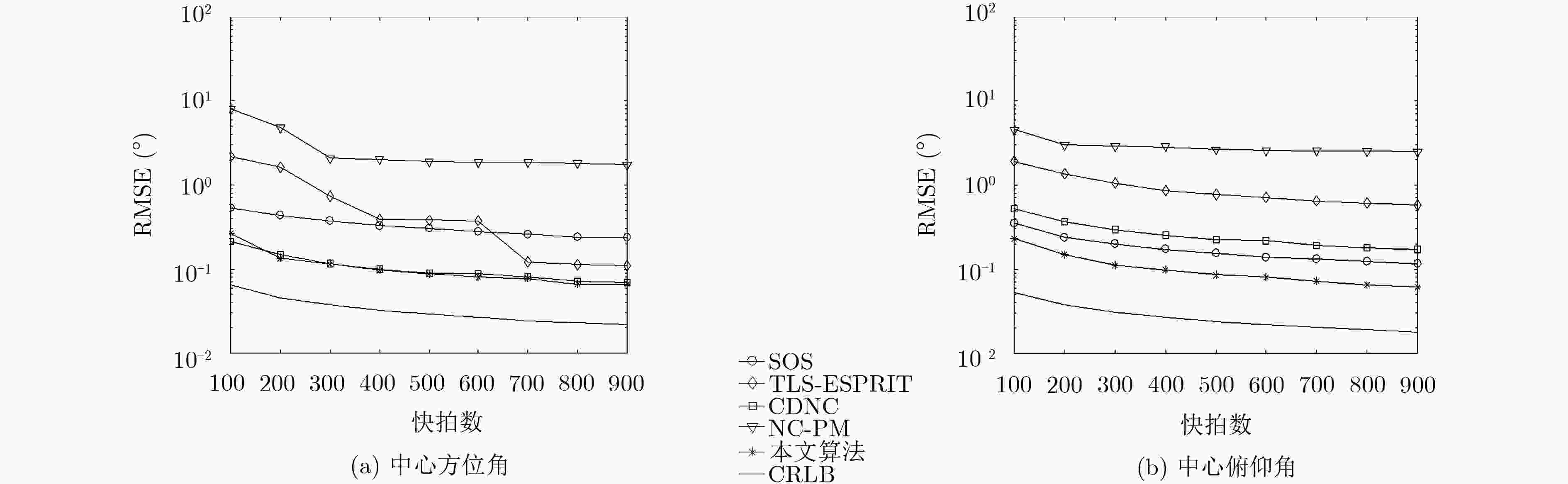
摘要: 在相干分布式非圆信号2维波达方向(DOA)估计中,针对利用非圆特性后维数扩展带来的较大复杂度问题,且现有的低复杂度算法均需要额外的参数匹配,该文提出一种基于互相关传播算子的自动匹配2维DOA快速估计算法。该算法考虑L型阵列,在建立相干分布式非圆信号扩展阵列模型的基础上,首先证明了L阵中两个子阵的广义方向矢量(GSV)均具有近似旋转不变特性,然后通过阵列输出信号的互相关运算消除了额外噪声,最终利用子阵GSV的近似旋转不变关系通过传播算子方法得到中心方位角与俯仰角估计。理论分析和仿真实验表明,所提算法无须谱峰搜索和协方差矩阵特征分解运算,具有较低的计算复杂度,并且能够实现2维DOA估计的自动匹配;同时,相比于现有的相干分布式非圆信号传播算子算法,所提算法以较小的复杂度代价获得了性能的较大提升。Abstract: In the two-dimensional Direction Of Arrival (DOA) estimation of coherently distributed noncircular sources, the problem of large complexity is caused by dimension expansion after exploiting noncircular property, meanwhile the existing low-complexity algorithms all require additional parameter pairing procedure. To solve these problems, a rapid DOA estimation algorithm with automatic pairing is proposed for coherently distributed noncircular sources based on cross-correlation propagator. The L-shaped array is considered. Firstly, the extended array manifold model is established by exploiting the noncircularity of the signal, and then it is proved that there are approximate rotational invariance relationships in the Generalized Steering Vectors (GSVs) of two subarrays of the L array. At the same time, the extra noise can be eliminated by the cross-correlation matrix of the array output signals. Finally, on the basis of the approximate rotational invariance relationships of the sub-arrays, the center azimuth and elevation DOAs can be obtained by propagator method. Theoretical analysis and simulation experiments show that without the spectrum searching and eigenvalue decomposition of the sample covariance matrix, the proposed algorithm has low computational complexity. Moreover, it can automatically pair the estimated central azimuth and central elevation DOAs. In addition, compared with the existing propagation method for coherently distributed noncircular sources, the proposed algorithm can achieve higher estimation accuracy with the small complexity cost.
-
表 1 计算复杂度对比
算法 计算量 SOS $O\left(8{M^3} + 4{M^2}N + L({K^3} + 2{K^2}M)\right)$ TLS-ESPRIT $O\left({(2M + 1)^3} + {(2M + 1)^2}N + 2M{K^2} + 2{K^3}\right)$ CDNC $O\left(64{M^3} + 16{M^2}N + \left(\frac{{11}}{9}M - 4\right){K^2} + 2{K^3}\right)$ NC-PM $O\left(2(4M - 1)KN + 2{K^3} + {K^2}\right)$ 本文算法 $O\left(4{M^2}N + 22{M^2}K + 3{K^3} - 12{K^2}\right)$ -
ZHANG Ying and NG B P. MUSIC-Like DOA estimation without estimating the number of sources[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1668–1676 doi: 10.1109/TSP.2009.2037074 樊劲宇, 顾红, 苏卫民, 等. 基于张量分解的互质阵MIMO雷达目标多参数估计方法[J]. 电子与信息学报, 2015, 37(4): 933–938 doi: 10.11999/JEIT140826FAN Jinyu, GU Hong, SU Weimin, et al. Co-prime MIMO radar multi-parameter estimation based on tensor decomposition[J]. Journal of Electronics&Information Technology, 2015, 37(4): 933–938 doi: 10.11999/JEIT140826 梁浩, 崔琛, 余剑. 基于ESPRIT算法的十字型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1): 80–89 doi: 10.11999/JEIT150402LIANG Hao, CUI Chen, and YU Jian. Reduced-dimensional DOA estimation based on ESPRIT algorithm in monostatic MIMO Radar with cross array[J]. Journal of Electronics&Information Technology, 2016, 38(1): 80–89 doi: 10.11999/JEIT150402 冯明月, 何明浩, 徐璟, 等. 低信噪比条件下宽带欠定信号高精度DOA估计[J]. 电子与信息学报, 2017, 39(6): 1340–1347 doi: 10.11999/JEIT160921FENG Mingyue, HE Minghao, XU Jing, et al. High accuracy DOA estimation under low SNR condition for wideband underdetermined signals[J]. Journal of Electronics&Information Technology, 2017, 39(6): 1340–1347 doi: 10.11999/JEIT160921 VALAEE S, CHAMPAGNE B, and KABAL P. Parametric localization of distributed sources[J]. IEEE Transactions on Signal Processing, 1995, 43(9): 2144–2153 doi: 10.1109/78.414777 郑植. 分布式信源低复杂度参数估计算法研究[D]. [博士论文], 电子科技大学, 2011.ZHENG Zhi. Research on low complexity parameter estimation algorithm for distributed source[D]. [Ph.D. dissertation], University of Electronic Science and Technology, 2011. CAO Renzheng, GAO Feifei, and ZHANG Xiaofei. An angular parameter estimation method for incoherently distributed sources via generalized shift invariance[J]. IEEE Transactions on Signal Processing, 2016, 64(17): 4493–4503 doi: 10.1109/TSP.2016.2557312 SHAHBAZPANAHI S, VALAEE S, and BASTANI M H. Distributed source localization using ESPRIT algorithm[J]. IEEE Transactions on Signal Processing, 2001, 49(10): 2169–2178 doi: 10.1109/78.950773 LV Tiejun, TAN Fangqing, GAO Hui, et al. A beamspace approach for 2-D localization of incoherently distributed sources in massive MIMO systems[J]. Signal Processing, 2016, 121(C): 30–45 doi: 10.1016/j.sigpro.2015.10.020 HASSANIEN A, SHAHBAZPANAHI S, and GERSHMAN A B. A generalized capon estimator for localization of multiple spread sources[J]. IEEE Transactions on Signal Processing, 2004, 52(1): 280–283 doi: 10.1109/TSP.2003.820089 SHAHBAZPANAHI S, VALAEE S, and GERSHMAN A B. A covariance fitting approach to parametric localization of multiple incoherently distributed sources[J]. IEEE Transactions on Signal Processing, 2004, 52(3): 592–600 doi: 10.1109/TSP.2003.822352 SIESKUL B T. An asymptotic maximum likelihood for joint estimation of nominal angles and angular spreads of multiple spatially distributed sources[J]. IEEE Transactions on Vehicular Technology, 2010, 59(3): 1534–1538 doi: 10.1109/TVT.2009.2040006 杨学敏, 李广军, 郑植. 基于稀疏表示的相干分布式非圆信号的参数估计[J]. 电子与信息学报, 2014, 36(1): 164–168 doi: 10.3724/SP.J.1146.2013.00444YANG Xuemin, LI Guangjun, and ZHENG Zhi. Parameters estimation of coherently distributed non-circular signal based on sparse representation[J]. Journal of Electronics&Information Technology, 2014, 36(1): 164–168 doi: 10.3724/SP.J.1146.2013.00444 BOUJEMAA H. Extension of COMET algorithm to multiple diffuse source localization in azimuth and elevation[J]. European Transactions on Telecommunications, 2005, 16(6): 557–566 doi: 10.1002/ett.1021 LEE J, SONG I, KWON H, et al. Low-complexity estimation of 2D DOA for coherently distributed sources[J]. Signal Processing, 2003, 83(8): 1789–1802 doi: 10.1016/S0165-1684(03)00103-8 ZHENG Zhi, LI Guangjun, and TENG Yunlong. Simplified estimation of 2D DOA for coherently distributed sources[J]. Wireless Personal Communications, 2012, 62(4): 907–922 doi: 10.1007/s11277-010-0100-y 尹洁昕, 吴瑛, 王鼎. 基于辅助阵元的非圆信号自校正算法及其性能分析[J]. 通信学报, 2014, 35(2): 153–165 doi: 10.3969/j.issn.1000-436x.2014.02.020YIN Jiexin, WU Ying, and WANG Ding. Auto-calibration method and performance analysis for noncircular sources based on instrumental sensors[J]. Journal on Communications, 2014, 35(2): 153–165 doi: 10.3969/j.issn.1000-436x.2014.02.020 SHI Yunmei, HUANG Lei, QIAN Cheng, et al. Direction-of-arrival estimation for noncircular sources via structured least squares-based esprit using three-axis crossed array[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1267–1278 doi: 10.1109/TAES.2015.140003 YANG Xuemin, LI Guangjun, ZHENG Zhi, et al. 2D DOA estimation of coherently distributed noncircular sources[J]. Wireless Personal Communications, 2014, 78(2): 1095–1102 doi: 10.1007/s11277-014-1803-2 DONG Yangyang, DONG Chunxi, XU Jin, et al. Computationally efficient 2-D DOA estimation for L-shaped array with automatic pairing[J]. IEEE Antennas&Wireless Propagation Letters, 2016, 15: 1669–1672 doi: 10.1109/LAWP.2016.2521785 LUO Jun, ZHANG Guoping, and YU Kegen. An automatically paired two-dimensional direction-of-arrival estimation method for two parallel uniform linear arrays[J]. AEU-International Journal of Electronics and Communications, 2017, 72: 46–51 doi: 10.1016/j.aeue.2016.11.017 YANG Xuemin, ZHENG Zhi, CHI C K, et al. Low-complexity 2D parameter estimation of coherently distributed noncircular signals using modified propagator[J]. Multidimensional Systems&Signal Processing, 2017, 28(2): 407–426 doi: 10.1007/s11045-015-0348-1 -





 下载:
下载:


 下载:
下载:
