Multi-dimensional Vandermonde Structure Based DOD-DOA and Doppler Frequency Estimation for Bistatic MIMO Radar
-
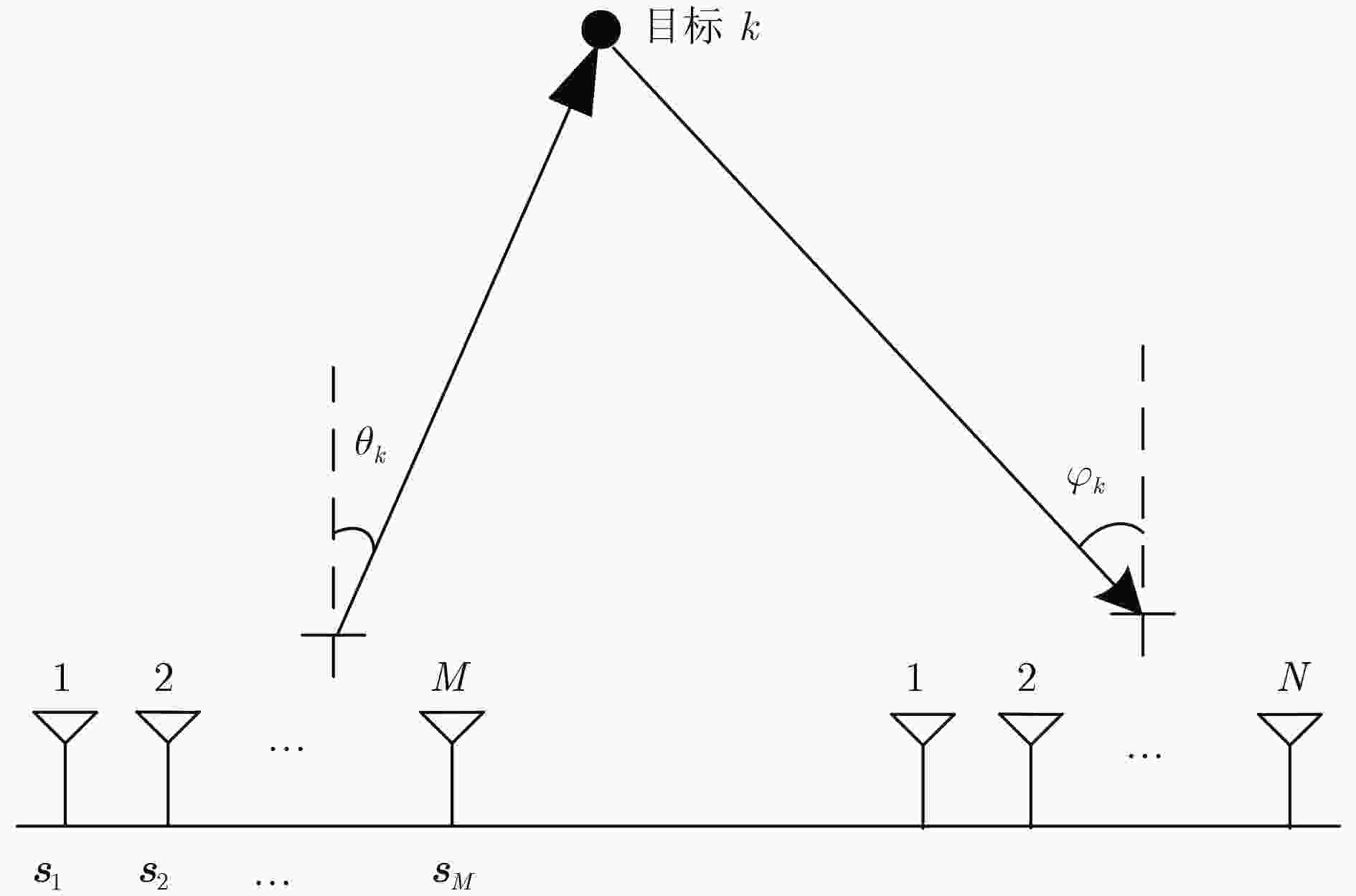
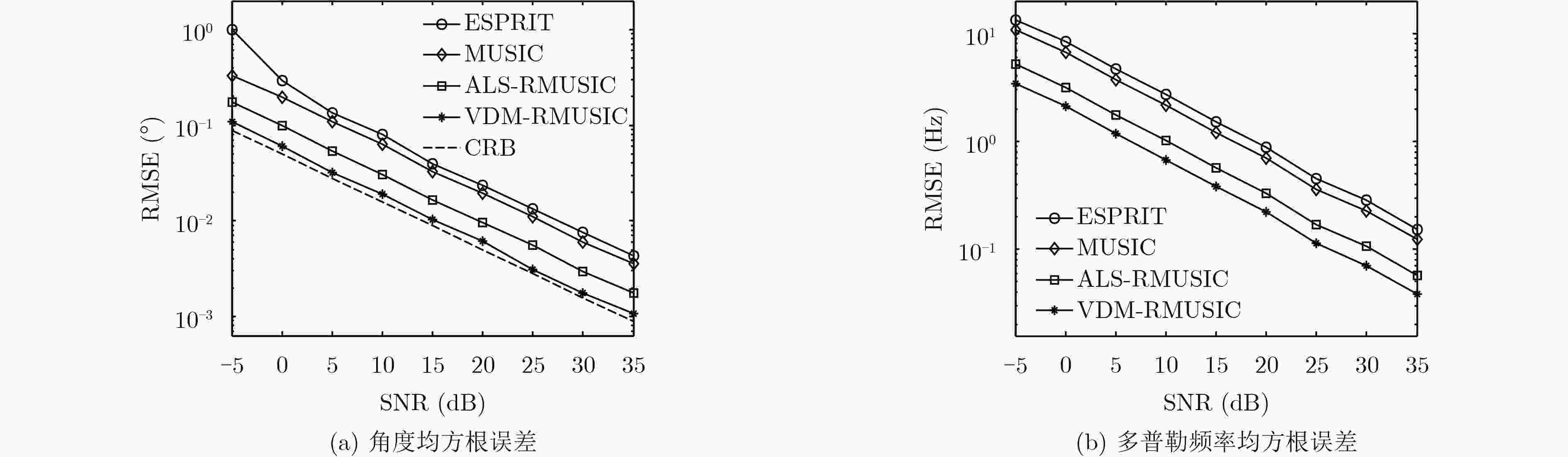
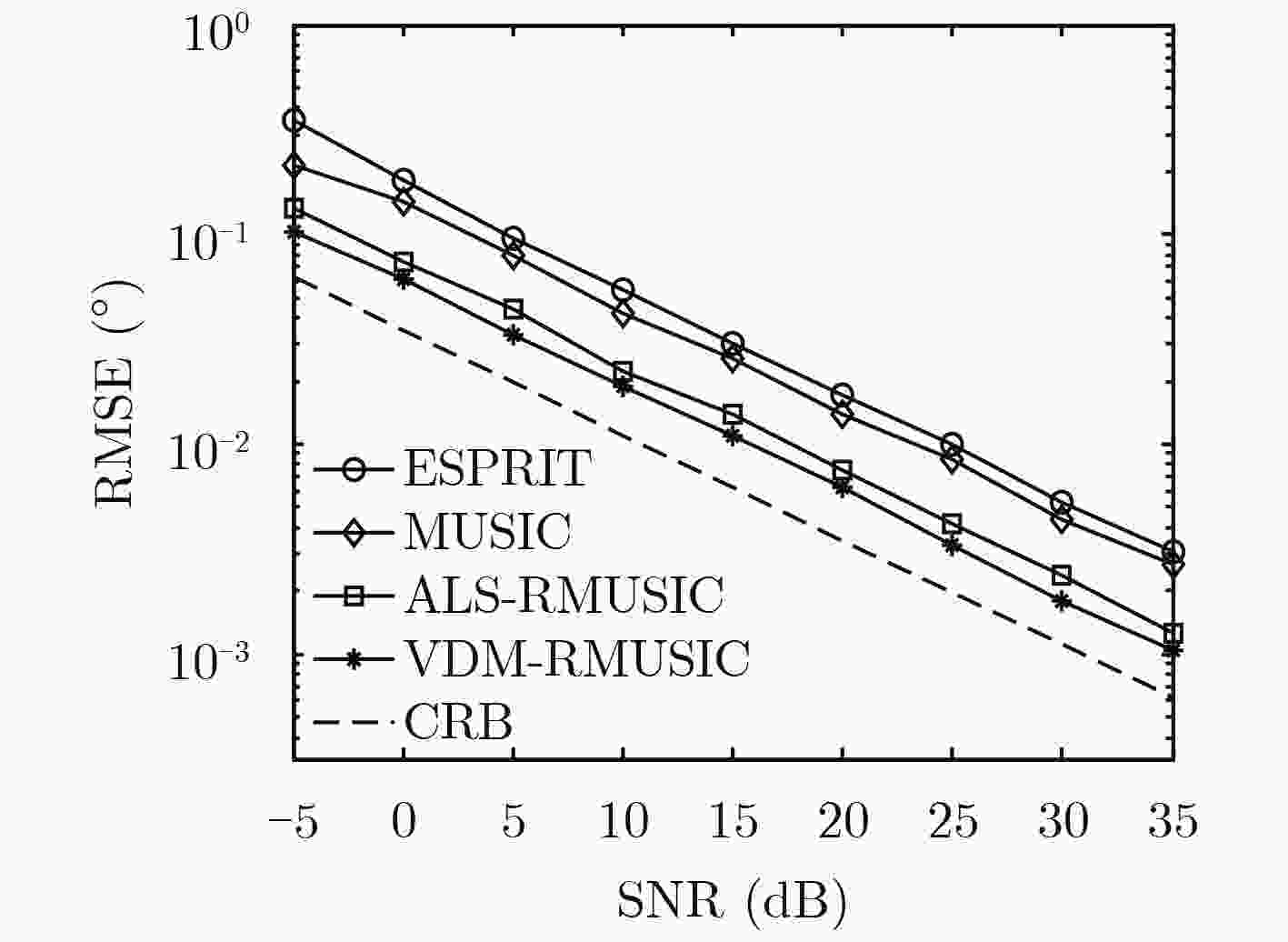
摘要: 针对双基地MIMO雷达收发角及多普勒联合频率估计问题,该文基于参数流型矩阵的多维范德蒙德结构特征,提出一种低运算量的3维参数联合估计算法。首先根据回波模型的多维结构特性构造3阶张量,并对其分别沿发射维、接收维和脉冲维切片得到3个等效矩阵;然后结合多维范德蒙德结构特征和等效矩阵的左奇异矩阵具有Khatri-Rao乘积结构特征,估计收发阵列流型矩阵和多普勒流型矩阵;最后通过Root-MUSIC算法估计收发角和多普勒频率。与现有算法相比,该算法显著改善了参数估计精度,在小脉冲数下,其运算量与旋转不变子空间算法(ESPRIT)相当。仿真实验验证了该算法的有效性。Abstract: In order to solve the problem of Direction Of Departure (DOD), Direction Of Arrival (DOA) and Doppler frequency estimation in bistatic MIMO radar, a low complexity method is proposed for joint estimation of the three parameters based on the multi-dimensional Vandermonde structure characteristic of the parameter manifold matrices. First, a third-order tensor is constructed according to the multi- dimensional structure of the echo model. Three equivalent matrices are obtained by cutting the tensor along transmit dimension, receive dimension and pulse dimension respectively. Then, combining the multi-dimensional Vandermonde characteristic with the Khatri-Rao product characteristic of the left-singular matrix of the equivalent matrix, transmit manifold matrix, receive manifold matrix and Doppler manifold matrix are estimated. Finally, the DOD, DOA and Doppler frequency are estimated by Root-MUSIC algorithm. Compared with the existence methods, the proposed algorithm improves obviously the estimation precision, and its computational cost is comparable to that of Estimation of Signal Parameters via Rotation Invariant Techniques (ESPRIT) method in small pulse number. The effectiveness of the proposed method is verified by simulation results.
-
表 1 基于多维范德蒙德结构的参数估计算法步骤
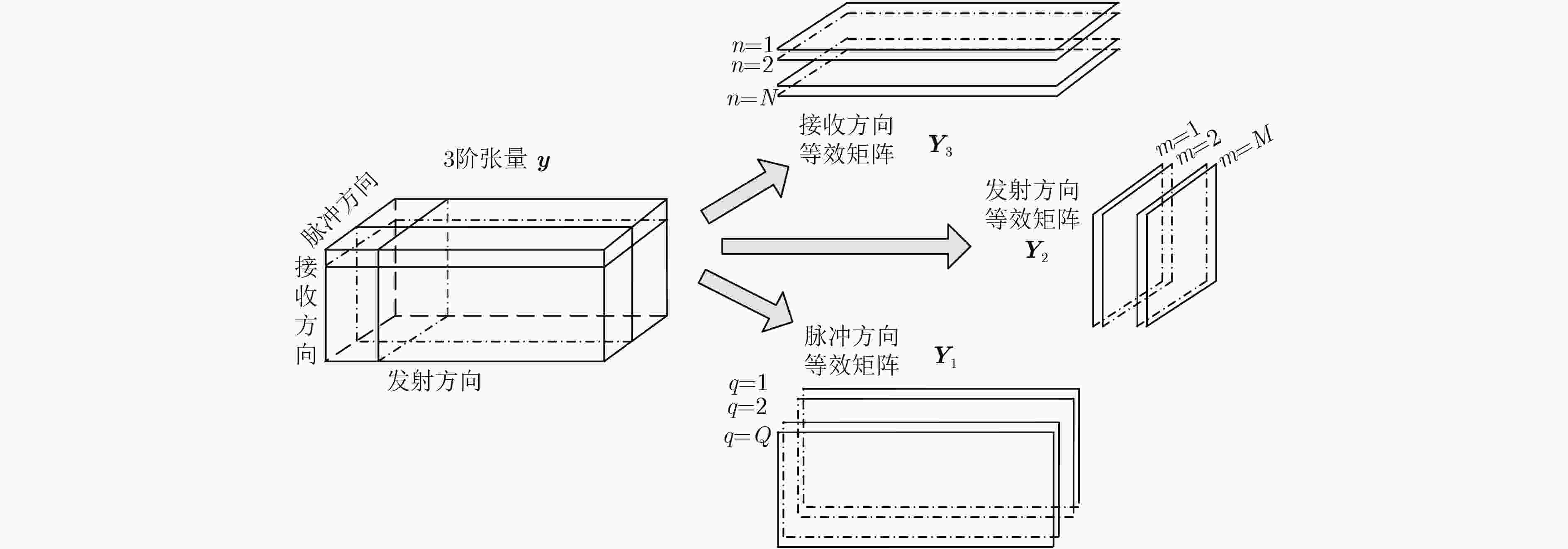
输入:匹配滤波输出的回波信号式(3)。 输出:目标收发角和多普勒频率估计值。 步骤1 根据式(3)的回波模型构造3阶张量,对其做3维展开,得到式(4)的等效矩阵 ${{Y}}_1,{{Y}}_2,{{Y}}_3$; 步骤2 对 ${{Y}}_1$做奇异值分解,根据式(10)计算矩阵 ${{F}}$;对 ${{F}}$特征值分解,利用其特征值和式(11)估计发射流型矩阵 ${{\widehat{{A}}}_1}$; 步骤3 据式(12)和式(13)计算接收流型矩阵 ${{\widehat{{B}}}_1}$,根据式(14)计算多普勒流型矩阵 ${{\widehat{{C}}}_1}$; 步骤4 用 ${{Y}}_2$代替 ${{Y}}_1$,重复步骤2和步骤3,得到 ${\widehat {{A}}_2},{\widehat {{B}}_2},{\widehat {{C}}_2}$;当目标散射特性服从Swerling-I模型时,用 ${{Y}}_3$代替 ${{Y}}_1$,重复步骤2和步骤3,
得到 ${\widehat {{A}}_3},{\widehat {{B}}_3},{\widehat {{C}}_3}$;步骤5 求解式(15),将误差剩余最小的一组作为最终流型矩阵的估计 $\widehat {{A}},\widehat {{B}},\widehat {{C}}$; 步骤6 采用Root-MUSIC算法处理步骤5得到的 $\widehat {{A}},\widehat {{B}},\widehat {{C}}$的每一列,估计收发角和多普勒频率。 -
TANG Bo and TANG Jun. Joint design of transmit waveforms and receive filters for MIMO radar space-time adaptive processing[J]. IEEE Transactions on Signal Processing, 2016, 64(18): 4707–4722 doi: 10.1109/TSP.2016.2569431 ZHANG Weitao , LOU Shunyian , LI Xiaojun, et al. Tracking multiple targets in MIMO radar via adaptive asymmetric joint diagonalization[J]. IEEE Transactions on Signal Processing, 2016, 64(11): 2880–2893 doi: 10.1109/TSP.2016.2535249 AITTOMAKI T and KOIVUNEN V. Mismatched filter design and interference mitigation for MIMO radars[J]. IEEE Transactions on Signal Processing, 2017, 65(2): 454–466 doi: 10.1109/TSP.2016.2620960 GUI Guolong, YU Xiangxiang, CAROTENUTO V, et al. Space-time transmit code and receive filter design for colocated MIMO radar[J]. IEEE Transactions on Signal Processing, 2017, 65(5): 1116–1129 doi: 10.1109/TSP.2016.2633242 LI Lin, CHENG Fangfang, and DAI Jisheng. Separate DOD and DOA estimation for bistatic MIMO radar[J]. International Journal of Antennas&Propagation, 2016, 25(8): 1–11 doi: 10.1155/2016/9170403 ZHANG Yu, ZHANG Gong, and WANG Xinhai. Computationally efficient DOA estimation for monostatic MIMO radar based on covariance matrix reconstruction[J]. Electronics Letters, 2017, 53(2): 111–113 doi: 10.1049/el.2016.3818 CHEN Jinli, GU Hong, and SU Weimin. A new method for joint DOD and DOA estimation in bistatic MIMO radar[J]. EURASIP Journal on Advances in Signal Processing, 2010, 90(2): 714–718 doi: 10.1016/sigpro.2009.08.003 梁浩, 崔琛, 余剑. 基于ESPRIT算法的十字型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1): 80–89 doi: 10.11999/JEIT150402LIANG Hao, CUI Chen, and YU Jian. Reduced-dimensional DOA estimation based on ESPRIT algorithm in monostatic MIMO radar with cross array[J]. Journal of Electronics&Informatio Technology, 2016, 38(1): 80–89 doi: 10.11999/JEIT150402 SRINIVASARAO C and PALANISAMY P. 2D-DOD and 2D-DOA estimation using the electromagnetic vector sensors[J]. Signal Processing, 2018, 147(6): 163–172 doi: 10.1016/j.sigpro.2018.01.025 HOKIGUCHI M, KIKUMA N, and SAKAKIBARA K. Target direction estimation by MIMO radar using root-MUSIC with minimum redundancy array[C]. IEEE International Symposium on Antennas & Propagation Conference, Okinawa, 2016: 1036–1037. ZHANG Dong, ZHANG Yongshun, HU Xiaowei, et al. Fast OMP algorithm for 3D parameters super-resolution estimation in bistatic MIMO radar[J]. Electronics Letters, 2016, 52(13): 1164–1166 doi: 10.1049/el.2016.0976 TIAN Ye, LIAN Qiusheng, and XU He. Sparse-reconstruction-based 2-D angle of arrival estimation with L-shaped array[J]. International Journal of Electronics and Communications, 2017, 72(2): 162–165 doi: 10.1016/j.aeue.2016.12.011 CHENG Yuanbing, GU Hong, and SU Weimin. Joint 4-D angle and Doppler shift estimation via tensor decomposition for MIMO array[J]. IEEE Communications Letters, 2012, 16(6): 917–920 doi: 10.1109/LCOMM.2012.040912.120298 CAO Mingyang, SERGIY A V, and ABOULNASR H. Transmit array interpolation for DOA estimation via tensor decomposition in 2-D MIMO radar[J]. IEEE Transactions on Signal Processing, 2017, 65(19): 5225–5239 doi: 10.1109/TSP.2017.2721904 LIU Shuangzhe and TRENKLER G. Hadamard, Khatri-Rao, Kronecker and other matrix products[J]. International Journal of Information and Systems Sciences, 2008, 4(1): 160–177. SIDIROPOULOS N, LATHAUWER L D, FU Xiao, et al. Tensor decomposition for signal processing and machine learning[J]. IEEE Transactions on Signal Processing, 2017, 65(13): 3551–3582 doi: 10.1109/TSP.2017.2690524 KOLDA T G and BADER B W. Tensor decomposition and application[J]. SIAM Review, 2009, 51(3): 455–500 doi: 10.1137/07070111X RICHARDS M A, SCHEER J A, and HOLM W A. Principles of Modern Radar: Basic Principles[M]. Raleigh, NC: SciTech Publishing, 2010: 263–266. 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 82–138.WANG Yongliang, CHEN Hui, PENG Yingning, et al. Theory and Algorithm for Spatial Spectrum Estimation[M]. Beijing: Tsinghua University Press, 2004: 82–138. GENE H G and CHARLES F V L. Matrix Computations[M]. Baltimore: Johns Hopkins University Press, 1996: 69–72. -





 下载:
下载:
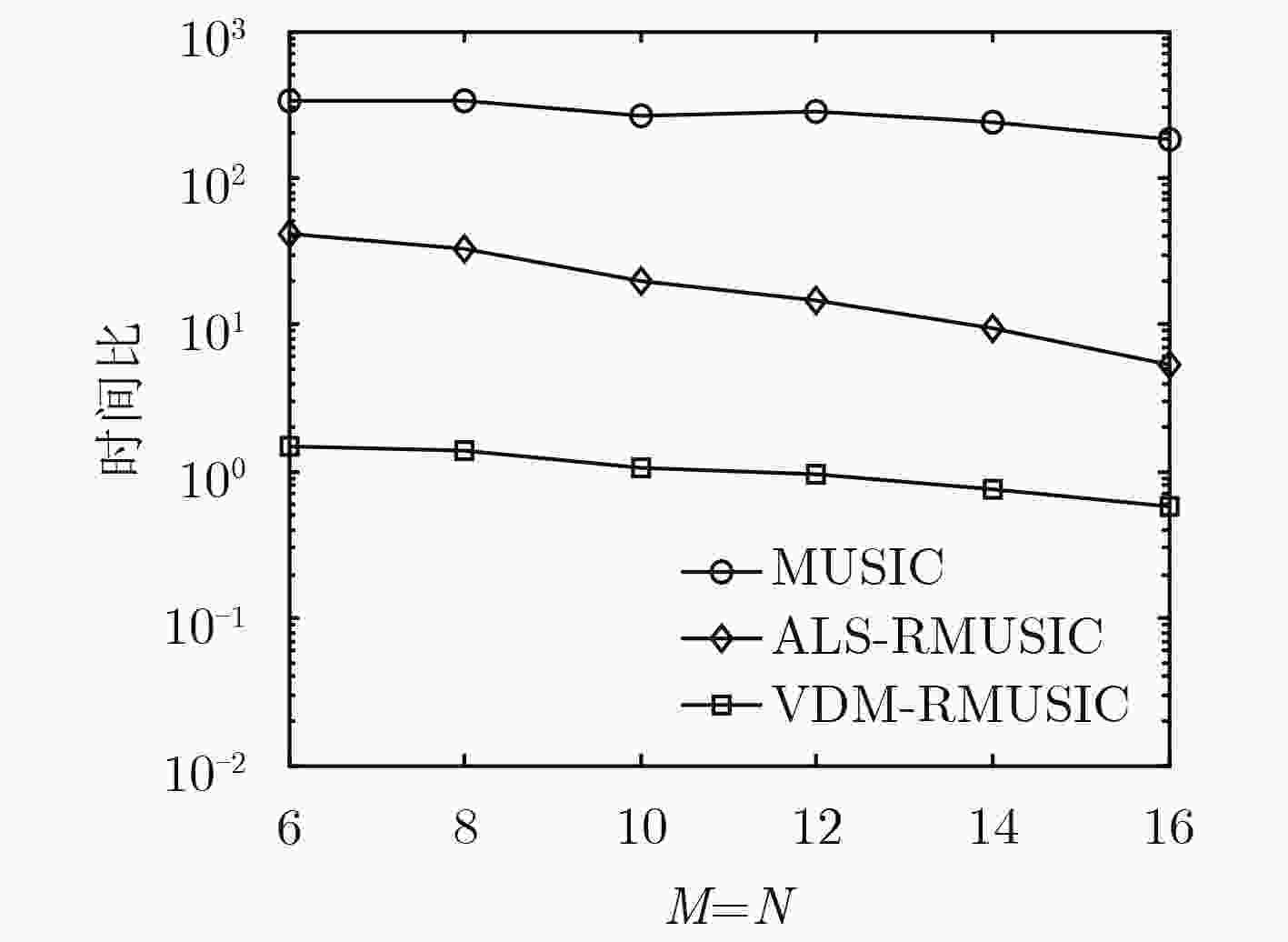


 下载:
下载:
