Efficient Ciphertext Deduplication and Auditing Scheme with Attribute-based Encryption
-
摘要:
针对当前支持去重的属性加密方案既不支持云存储数据审计,又不支持过期用户撤销,且去重搜索和用户解密效率较低的问题,该文提出一种支持高效去重和审计的属性加密方案。该方案引入了第3方审计者对云存储数据的完整性进行检验,利用代理辅助用户撤销机制对过期用户进行撤销,又提出高效去重搜索树技术来提高去重搜索效率,并通过代理解密机制辅助用户解密。安全性分析表明该方案通过采用混合云架构,在公有云达到IND-CPA安全性,在私有云达到PRV-CDA安全性。性能分析表明该方案的去重搜索效率更高,用户的解密计算量较小。
Abstract:Existing attribute-based deduplication schemes can support neither auditing of cloud storage data nor revocation of expired users. On the other hand, they are less efficient for deduplication search and users decryption. In order to solve these problems, this paper proposes an efficient deduplication and auditing Attribute-Based Encryption (ABE) scheme. A third-party auditor is introduced to verify the integrity of cloud storage data. Through an agent auxiliary user revocation mechanism, the proposed scheme supports the revocation of expired users. Effective deduplication search tree is put forward to improve the search efficiency, and the proxy decryption mechanism is used to assist users to decrypt. Finally, the security analysis shows that the proposed scheme can achieve IND-CPA security in the public cloud and PRV-CDA security in the private cloud by resorting to the hybrid cloud architecture. The performance analysis shows that the deduplication search is more efficient and the computation cost of user encryption is smaller.
-
Key words:
- Attribute-Based Encryption (ABE) /
- Data deduplication /
- Auditing /
- Users revocation /
- Proxy decryption
-
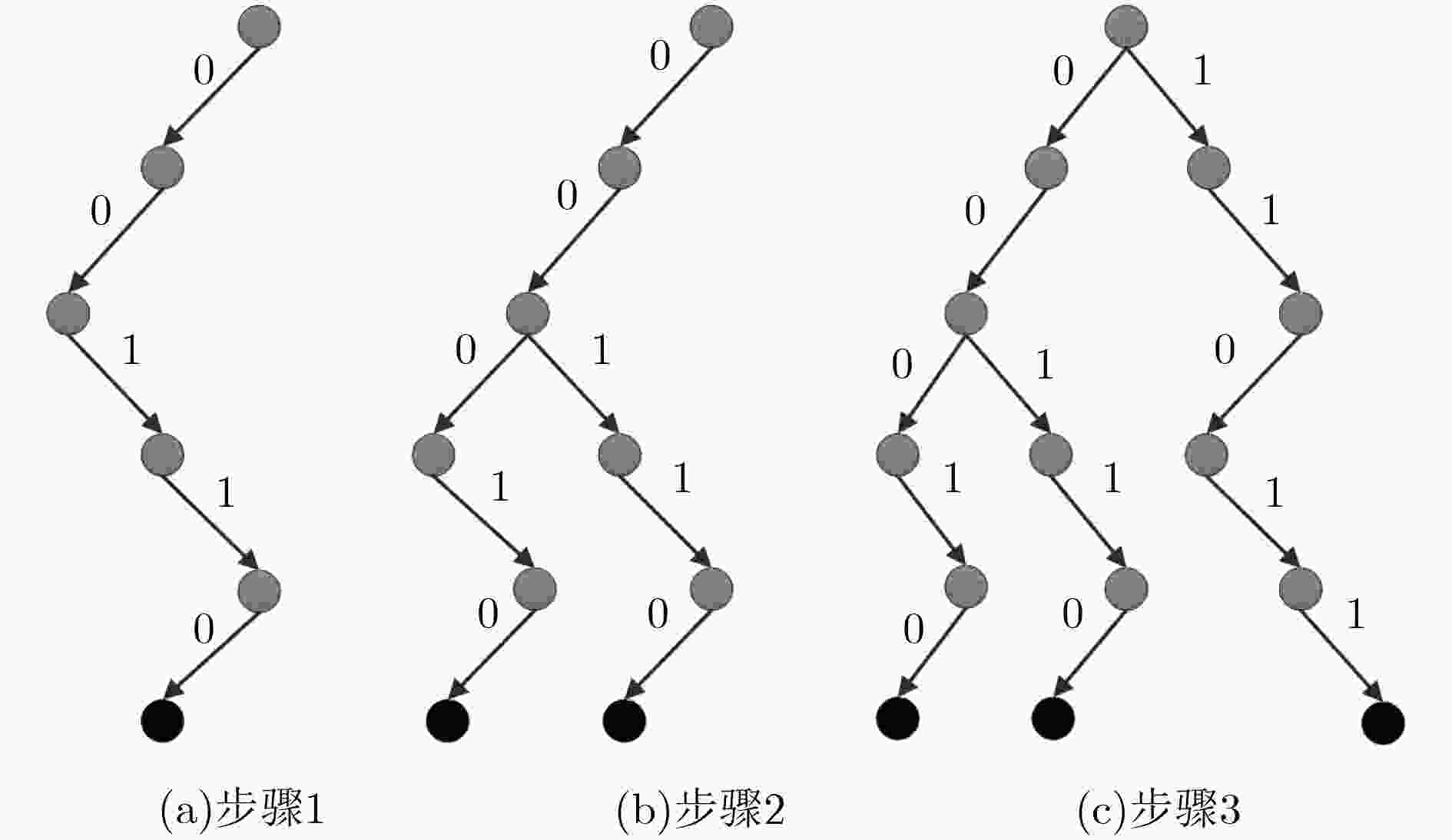
表 1 高效去重搜索树构造
算法 1 高效去重搜索树构造 假设私有云需要存储密文元组${{\rm{CT}} _i}$的指针到EDST叶子节点。(初
始化时,当前节点从根节点开始。假设$\left| {{T_{2,i}}} \right| $=60 bit。)步骤 1 若$1 \le j < 60$时,私有云判断标签${T_{2,i}}$第$j$位。如果第$j$位
是0,密文元组${{\rm{CT}} _i}$的指针移动到当前节点的左子节点;
否则移动到右子节点。步骤 2 若$j = 60$时,私有云判断标签${T_{2,i}}$第60位。如果第60位是0,密文元组${{\rm{CT}} _i}$的指针移动到当前节点的左子节点,并在当前节点存储密文元组${{\rm{CT}} _i}$的指针;否则移动到右子节点,并在当前节点存储密文元组${{\rm{CT}} _i}$的指针。 表 2 数据在高效去重搜索树上去重搜索
算法 2 数据在高效去重搜索树上去重搜索 $U\,$发送密文元组${{\rm{CT}} _i}$到私有云,私有云收到${{\rm{CT}} _i}$后,它开始从根
节点检查重复数据。(初始化时,当前节点从根节点开始。)步骤 1 若$1 \le j < 60$时,私有云判断标签${T_{2,i}}$第$j$位; (1)如果第$j$位是0。若当前节点有左子节点,则密文元组${{\rm{CT}} _i}$的
指针移动到当前节点的左子节点;否则,重复数据没有找到;(2)如果第$j$位是1。若当前节点有右子节点,则密文元组${{\rm{CT}} _i}$的
指针移动到当前节点的右子节点;否则,重复数据没有找到。步骤 2 若$j = 60$时,私有云判断标签${T_{2,i}}$第60位; (1)如果第60位是0。若当前节点有左子节点,则密文元组${{\rm{CT}} _i}$
的指针移动到当前节点的左子节点,转(3)步;否则,重复
数据没有找到;(2)如果第60位是1。若当前节点有右子节点,则密文元组${{\rm{CT}} _i}$
的指针移动到当前节点的右子节点,转(3)步;否则,重复
数据没有找到;(3)密文元组${{\rm{CT}} _i}$的指针找到密文元组${{\rm{CT}} _j}$,私有云判断等式
$e({g^{{H_1}(m){\mu _i}}},{g^{{\mu _j}}}) = e({g^{{H_1}(m){\mu _j}}},{g^{{\mu _i}}})$是否成立。若成立,则重复
数据找到;否则,重复数据没有找到。 -
CHOO K K R, HERMAN M, IORGA M, et al. Cloud forensics: State-of-the-art and future directions[J]. Digital Investigation, 2016, 18: 77–78. doi: 10.1016/j.diin.2016.08.003 LAI Junzuo, DENG R H, and LI Yingjun. Fully secure cipertext-policy hiding CP-ABE[C]. International Conference on Information Security Practice and Experience, Guangzhou, China, 2011: 24–39. doi: https://doi.org/10.1007/978-3-642-21031-0_3. YU Shucheng, WANG Cong, REN Kui, et al. Achieving secure, scalable, and fine-grained data access control in cloud computing[C]. Proceedings of the 29th Conference on Information Communications, San Diego, USA, 2010: 1–9. ROUSELAKIS Y and WATERS B. Practical constructions and new proof methods for large universe attribute-based encryption[C]. ACM Sigsac Conference on Computer & Communications Security, Berlin, Germary, 2013: 463–474. BELLARE M, KEELVEEDHI S, and RISTENPAR T. Message-locked encryption and secure deduplication[C]. Annual International Conference on the Theory and Applications of Cryptographic Techniques, Athens, Greece, 2013: 296–312. doi: https://doi.org/10.1007/978-3-642-38348-9_18. BELLARE M and KEELVEEDHI S. Interactive messagee- locked encryption and secure deduplication[C]. IACR International Workshop on Public Key Cryptography, Gaithersburg, USA, 2015: 516–538. doi: https://doi.org/10.1007/978-3-662-46447-2_23. CUI Hui, DENG R H, LI Yingjiu, et al. Attribute-based storage supporting secure deduplication of encrypted data in cloud[J]. IEEE Transactions on Big Data, 2017(99): 1–13. doi: 10.1109/TBdata.2017.2656120 JIANG Tao, CHEN Xiaofeng, WU Qianhong, et al. Secure and efficient cloud data deduplication with randomized tag[J]. IEEE Transactions on Information Forensics and Security, 2017, 12(3): 532–543. doi: 10.1109/TIFS.2016.2622013 YANG Xue, LU Rongxing, CHOO K K R, et al. Achieving efficient and privacy-preserving cross-domain big data deduplication in cloud[J]. IEEE Transactions on Big Data, 2017(99): 1–12. doi: 10.1109/TBDATA.2017.2721444 YU Yong, LI Yannan, NI Jianbing, et al. Comments on " public integrity auditing for dynamic data sharing with multiuser modification”[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(3): 658–659. doi: 10.1109/TIFS.2015.2501728 YANG Guangyuan, YU Jia, SHEN Wenting, et al. Enabling public auditing for shared data in cloud storage supporting identity privacy and traceability[J]. Journal of Systems and Software, 2016, 113: 130–139. doi: 10.1016/j.jss.2015.11.044 SHEN Jian, SHEN Jun, CHEN Xiaofeng, et al. An efficient public auditing protocol with novel dynamic structure for cloud data[J]. IEEE Transactions on Information Forensics and Security, 2017, 12(10): 2402–2415. doi: 10.1109/TIFS.2017.2705620 YAN Xuewei, MA Hua, LIU Zhenhua, et al. Large universe revocable fine-grained encryption with public auditing [C]. International Conference on Broadband and Wireless Computing, Communication and Applications, Asan, Korea, 2016: 823–830. doi: https://doi.org/10.1007/978-3-319-49106-6_84. 王光波, 王建华. 基于属性加密的云存储方案研究[J]. 电子与信息学报, 2016, 38(11): 2931–2939. doi: 10.11999/JEIT160064WANG Guangbo and WANG Jianhua. Research on cloud storage scheme with attribute-based encryption[J]. Journal of Electronics &Information Technology, 2016, 38(11): 2931–2939. doi: 10.11999/JEIT160064 -





 下载:
下载:


 下载:
下载:
