An Improved Algorithm of Product of Experts System Based on Restricted Boltzmann Machine
-
摘要: 深度学习在高维特征向量的信息提取和分类中具有很强的能力,但深度学习训练时间也比较长,超参数搜索空间大,从而导致超参数寻优较困难。针对此问题,该文提出一种基于受限玻尔兹曼机(RBM)专家乘积系统的改进方法。先将专家乘积系统原理与RBM算法相结合,采用全是真实概率值的参数更新方式会引起模型识别效果不理想和带来密度问题,为此将其更新方式进行改进;为加快网络收敛和提高模型识别能力,采取在RBM预训练阶段和微调阶段引入不同组合方式动量项的一种改进算法。通过对MNIST数据库中的0~9的手写数字体的识别和CMU-PIE数据库的人脸识别实验,提出的算法减少了学习时间,提高了超参数寻优的效率,进而构建的深层网络能获得较好的分类效果。试验结果表明,提出的改进算法在处理高维大量的数据时,计算效率有较大提高,其算法有效。Abstract: Deep learning has a strong ability in the high-dimensional feature vector information extraction and classification. But the training time of deep learning is so long that the optimal hyper-parameters combination can not be found in a short time. To solve these problems, a method of product of experts system based on Restricted Boltzmann Machine (RBM) is proposed. The product of experts theory is combined with the RBM algorithm and the parameter updating way is all adopted the probability value, which leads to the undesirable recognition effect and slightly worse density models, so the parameter updating way is improved. An improved algorithm with momentum terms in different combinations is used not only in the RBM pre-training phase but also in the fine-tuning stage for both classification accuracy enhancement and training time decreasing. Through the recognition experiments on the MNIST database and CMU-PIE face database, the proposed algorithm reduces the training time, and improves the efficiency of hyper-parameters optimization, and then the deep belief network can achieve better classification performance. The result shows that the improved algorithm can improve both accuracy and computation efficiency in dealing with high-dimensional and large amounts of data, the new method is effective.
-
表 1 RBM学习算法的主要步骤
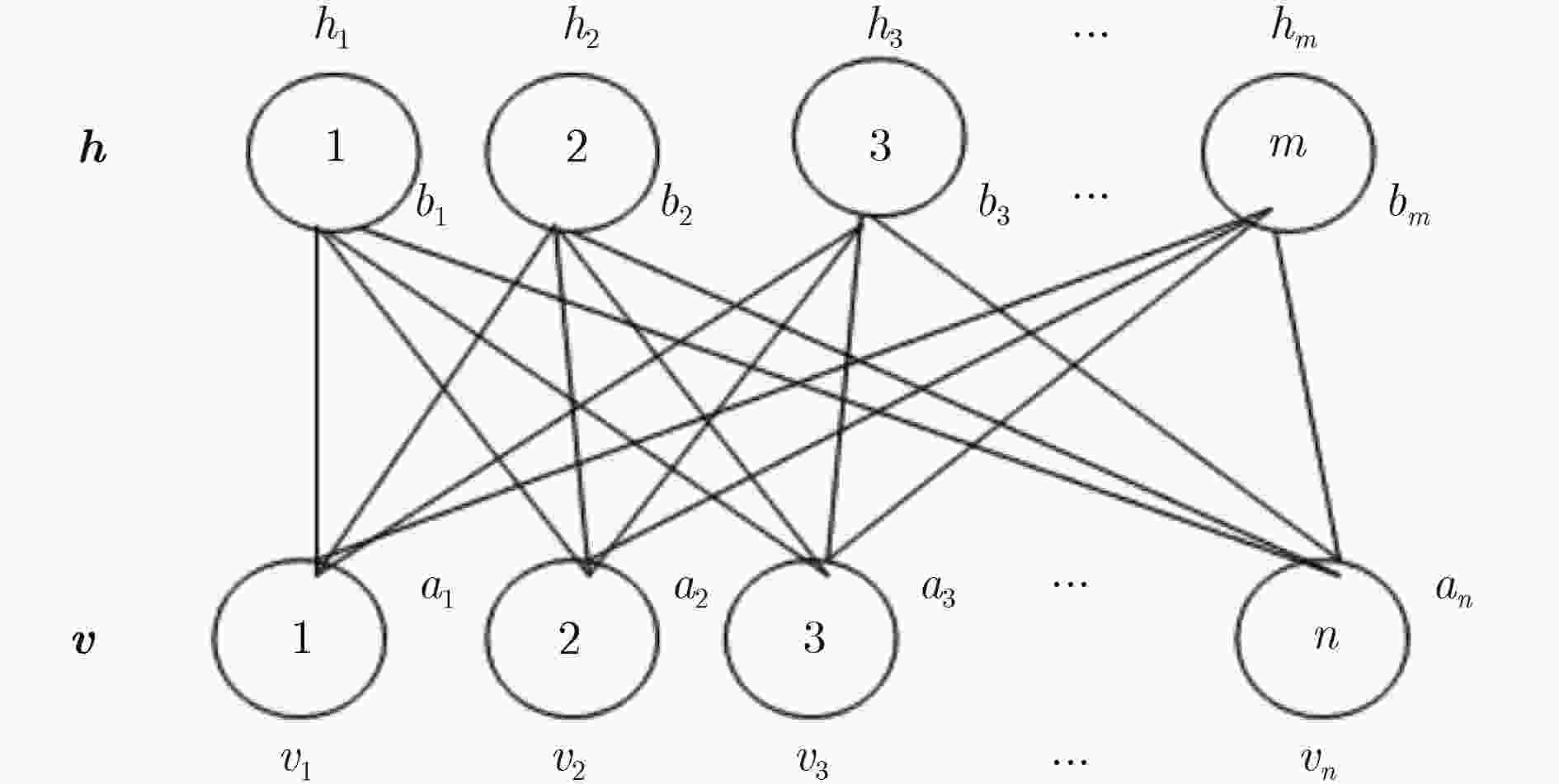
(1) 输入训练样本集合 $S = \left\{ {{{v}}^1},{{{v}}^2}, ·\!·\!· ,{{{v}}^T}\right\} $或者 $S = \left\{ {{{d}}^1},{{{d}}^2}, ·\!·\!· ,{{{d}}^T}\right\} $,
每一批有 $S = B = T\,$个训练样本,设置可见层的单元个数 $n$,隐
单元个数 $m$,学习率 $\eta $,动量项 ${m^*}$
(2) 初始化:随机初始化 $\Delta {w_{ij}} = \Delta {a_i} = \Delta {b_j} = 0$ For
$i = 1,2, ·\!·\!· ,n;j = 1,2, ·\!·\!· ,m$
(3) 在每个RBM中,对所有的训练样本 ${{d}} \in S$
(4) $ {{{v}}^{(0)}} \leftarrow {{v}} = {{d}}$
(5) For $t = 0,1, ·\!·\!· ,k - 1$
(6) Gibbs 采样: For $j = 1,2, ·\!·\!· ,m$,采样 $h_j^{(t)} \sim p\left({h_j}\left| {{{{v}}^{(t)}}} \right.\right)$
(7) For $i = 1,2, ·\!·\!· ,n$,采样 $v_i^{(t + 1)} \sim p\left({v_i}\left| {{{{h}}^{(t)}}} \right.\right)$
(8) End for
(9) For $i = 1,2, ·\!·\!· ,n;j = 1,2, ·\!·\!· ,m$
(10) 一个训练样本时,参数更新:
(11) $\Delta {w_{ij}} \leftarrow {m^*} \cdot \Delta {w_{ij}} + \eta \left[v_i^{(0)}p\left({h_j} = 1|{v^{({0})}}\right) - p\left({v_i} = 1\left| {{{{h}}^{(1)}}} \right.\right)\right.$
$\left. \cdot p\left({h_j} = 1\left| {{{{v}}^{(1)}}} \right.\right)\right]$
(12) $\Delta {a_i} \leftarrow {m^*} \cdot \Delta {a_i} + \eta \left[v_i^{(0)} - p\left({v_i} = 1\left| {{{{h}}^{(1)}}} \right.\right)\right]$
(13) $\Delta {b_j} \leftarrow {m^*} \cdot \Delta {b_j} + \eta \left[h_j^{(0)} - p\left({h_j} = 1\left| {{{{v}}^{(1)}}} \right.\right)\right]$
(14) End for表 2 两种RBM模型在MNIST数据集上的实验情况(隐单元个数、时间、错误率)
表 3 不同模型在MNIST数据集上的实验结果(错误率)
-
LIAO S H. Expert system methodologies and applications-a decade review from 1995 to 2004[J]. Expert Systems with Applications, 2005, 28: 93–103 doi: 10.1016/j.eswa.2004.08.003 VUNDAVILLI PANDU R, PHANI KUMAR J, SAI PRIYATHAM CH, et al. Neural network-based expert system for modeling of tube spinning process[J]. Neural Computing and Application, 2015, 26(6): 1481–1493 doi: 10.1007/s00521-015-1820-4 MAYRAZ G and HINTON G E. Recognizing handwritten digits using hierarchical products of experts[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(2): 189–197 doi: 10.1109/34.982899 焦李成, 杨淑媛, 刘芳, 等. 神经网络七十年: 回顾与展望[J]. 计算机学报, 2016, 39(1): 1–21 doi: 10.11897/SP.J.1016.2016.01697JIAO Licheng, YANG Shuyuan, LIU Fang, et al. Neural network in seventy: Retrospect and prospect[J]. Chinese Journal of Computers, 2016, 39(1): 1–21 doi: 10.11897/SP.J.1016.2016.01697 HINTON G E. Training products of experts by minimizing contrastive divergence[J]. Neural Computation, 2002, 14(8): 1711–1800 doi: 10.1162/089976602760128018 罗剑江, 王振友. 一种提高受限玻尔兹曼机性能的反正切函数逼近L0范数方法[J]. 小型微型计算机系统, 2016(11): 2562–2566LUO Jianjiang and WANG Zhenyou. Enhancing performance of restricted Boltzmann machine using Arctan approximation of L0 norm[J]. Journal of Chinese Computer Systems, 2016(11): 2562–2566 王岳青, 窦勇, 吕启, 等. 基于异构体系结构的并行深度学习编程框架[J]. 计算机研究与发展, 2016, 53(6): 1202–1210 doi: 10.7544/issn1000-1239.2016.20150147WANG Yueqing, Dou Yong, Lü Qi, et al. A parallel deep learning programming framework based on heterogeneous architecture[J]. Journal of Computer Research and Development, 2016, 53(6): 1202–1210 doi: 10.7544/issn1000-1239.2016.20150147 ZHANG Chunyang, CHEN Philip, CHEN Dewang, et al. MapReduce based distributed learning algorithm for Restricted Boltzmann Machine[J]. Neurocomputing, 2016(198): 4–11 doi: 10.1016/j.neucom.2015.09.129 POLYAK T. Some methods of speeding up the convergence of iteration methods[J]. USSR Computational Mathematics and Mathematical Physics, 1964, 4(5): 1–17 doi: 10.1016/0041-5553(64)90137-5 SUTSKEVER I, MARTENS J, DAHL G, et al. On the importance of initialization and momentum in deep learning[C]. Proceedings of International Conference on Machine Learning, Atlanta, USA, 2013: 1139–1147. ZAREBA S, GONCZAREK A, TOMCZAK J M, et al. Accelerated learning for restricted Boltzmann machine with momentum term[C]. Proceedings of International Conference on Systems Engineering, Coventry, UK, 2015: 187–192. YUAN Kun, YING Bicheng, and SAYED A H. On the influence of momentum acceleration on online learning[J]. Journal of Machine Learning Research, 2016(17): 1–66. HINTON G E. A practical guide to training restricted Boltzmann machines[R]. Toronto: Machine Learning Group, University of Toronto, 2012: 599–619. FISCHER A and CHRISTIAN I. Training restricted Boltzmann machines: An introduction[J]. Pattern Recognition, 2014, 47: 25–39. doi: 10.1007/s13218-015-0371-2 SMOLENSKY P. Information Processing in Dynamical Systems: Foundations of Harmony Theory[M]. Cambridge, MA: MIT Press, 1986: 195–280. ROUX N L and BENGIO Y. Representational power of restricted Boltzmann machines and deep belief networks[J]. Neural Computation, 2008, 20(6): 1631–1649 doi: 10.1162/neco.2008.04-07-510 HINTON G E, OSINDERO S, and TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527–1554 doi: 10.1162/neco.2006.18.7.1527 FREUND Y and HAUSSLER D. Unsupervised learning of distributions on binary vectors using two layer networks[J]. Advances in Neural Information Processing Systems, 1992, 4: 912–919. PETERSON C and ANDERSON J R. A mean field theory learning algorithm for neural networks[J]. Complex Systems, 1987, 1: 995–1019. RUMELHART D E, HINTON G E, and WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323: 533–536 doi: 10.1038/323533a0 DECOSTE D and SCHOELKOPF B. Training invariant support vector machines[J]. Machine Learning, 2002, 46: 161–190. 郭继昌, 张帆, 王楠. 基于Fisher约束和字典对的图像分类[J]. 电子与信息学报, 2017, 39(2): 270–277 doi: 10.11999/JEIT160296GUO Jichang, ZHANG Fan, and WANG Nan. Image classification based on Fisher constraint and dictionary pair[J]. Journal of Electronics&Information Technology, 2017, 39(2): 270–277 doi: 10.11999/JEIT160296 付晓, 沈远彤, 付丽华, 等. 基于特征聚类的稀疏自编码快速算法[J]. 电子学报, 2018, 46(5): 1041–1046 doi: 10.3969/j.issn.0372-2112.2018.05.003FU Xiao, SHEN Yuan-tong, FU Li-hua, et al. An optimized sparse auto-encoder network based on feature clustering[J]. Acta Electronica Sinica, 2018, 46(5): 1041–1046 doi: 10.3969/j.issn.0372-2112.2018.05.003 李倩玉, 蒋建国, 齐美彬. 基于改进深层网络的人脸识别算 法[J]. 电子学报, 2017, 45(3): 619–625 doi: 10.3969/j.issn.0372-2112.2017.03.017LI Qianyu, JIANG Jianguo, and QI Meibin. Face recognition algorithm based on improved deep networks[J]. Acta Electronica Sinica, 2017, 45(3): 619–625 doi: 10.3969/j.issn.0372-2112.2017.03.017 -





 下载:
下载:





 下载:
下载:
