基于公理化模糊子集的改进谱聚类算法

赵小强; 刘晓丽

doi:10.11999/IEIT170904

基于公理化模糊子集的改进谱聚类算法

doi: 10.11999/IEIT170904

赵小强^{1, 2, 3, ,},
刘晓丽¹

1.
兰州理工大学电气工程与信息工程学院兰州 730050
2.
甘肃省工业过程先进控制重点实验室兰州 730050
3.
兰州理工大学国家级电气与控制工程实验教学中心兰州 730050

基金项目: 国家自然科学基金(61763029)，甘肃省基础研究创新群体基金(1506RJIA031)

详细信息

作者简介:
赵小强：男，1969年生，博士生导师，教授，主要研究方向为数据挖掘、故障诊断、图像处理、污水处理、生产调度等

刘晓丽：女，1992年生，硕士生，研究方向为数据挖掘

通讯作者:
赵小强 xqzhao@lut.cn

中图分类号: TP181
计量
- 文章访问数: 2043
- HTML全文浏览量: 689
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2017-09-25
- 修回日期: 2018-05-02
- 网络出版日期: 2018-05-30
- 刊出日期: 2018-08-01

An Improved Spectral Clustering Algorithm Based on Axiomatic Fuzzy Set

Xiaoqiang ZHAO^{1, 2, 3
, ,},
Xiaoli LIU¹

1.
College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China
2.
Key Laboratory of Gansu Advanced Control for Industrial Processes, Lanzhou 730050, China
3.
National Experimental Teaching Center of Electrical and Control Engineering, Lanzhou University of Technology, Lanzhou 730050, China

Funds: The National Natural Science Foundation of China (61763029), The Gansu Province Basic Research Innovation Group Fund (1506RJIA031)

摘要

摘要: 谱聚类算法通常是采用高斯核作为相似性度量，并利用所有可用的特征来构建具有欧氏距离的相似度矩阵，数据集复杂度会影响其谱聚类性能，因此该文提出一种基于公理化模糊子集(AFS)的改进谱聚类算法。首先结合AFS算法，利用识别特征来衡量更合适的数据成对相似性，生成更强大的亲合矩阵；再有效地利用Nyström采样算法，计算采样点间以及采样点和剩余点间的相似度矩阵去降低计算的复杂度；最后通过在不同数据集以及图像分割上进行实验，证明了提出算法的有效性。
- 亲和矩阵 /
- 谱聚类 /
- 公理化模糊子集 /
- Nyström采样算法
Abstract: Gaussian kernel is usually used as the similarity measure in spectral clustering algorithm, and all the available features are used to construct the similarity matrix with Euclidean distance. The complexity of the data set would affect its spectral clustering performance. Therefore, an improved spectral clustering algorithm based on Axiomatic Fuzzy Set (AFS) is proposed. Firstly, AFS algorithm is combined to measure the similarity of more suitable data by recognizing features, and the stronger affinity matrix is generated. Then Nyström sampling algorithm is used to calculate the similarity matrix between the sampling points and the sampling points and the remaining points to reduce the computational complexity. Finally, the experiment is carried out by using different data sets and image segmentations, the effectiveness of the proposed algorithm are proved.
- Affinity matrix /
- Spectral clustering /
- Axiomatic Fuzzy Set (AFS) /
- Nyström sampling algorithm

HTML全文

图 1 原图

下载: 全尺寸图片幻灯片

图 2 谱聚类算法分割结果

下载: 全尺寸图片幻灯片

图 3 本文算法分割结果

下载: 全尺寸图片幻灯片

表 1 数据集特征

数据集	数据总数	类数	维数
Iris	150	3	4
Heart	270	2	13
Sonar	208	2	60
Wine	178	3	13
Protein	552	8	77
Hepatitis	155	2	19
Segmentation	2310	7	19
Pen digits	10992	10	16

下载: 导出CSV

表 2 数据集的CE(%)

数据集	SC	STSC	AFS	本文算法
Iris	10.71	7.46	9.72	7.63
Heart	20.96	22.13	30.63	12.42
Sonar	44.53	46.83	38.52	33.60
Wine	2.92	2.91	3.54	3.13
Protein	54.70	55.67	55.12	48.87
Hepatitis	30.76	38.73	32.34	23.20
Segmentation	22.08	21.35	31.17	18.63
Pen digits	25.37	24.25	–	22.16

下载: 导出CSV

表 3 数据集的NMI(%)

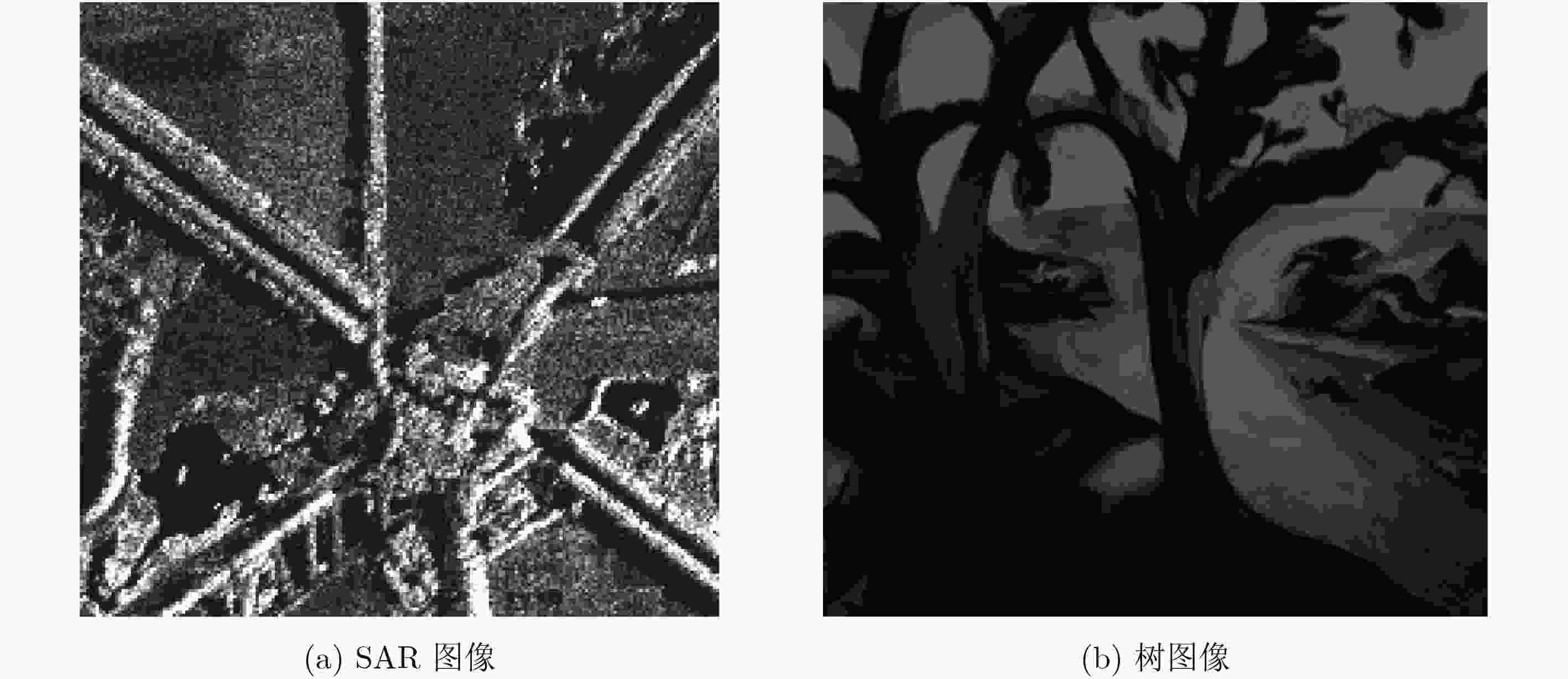
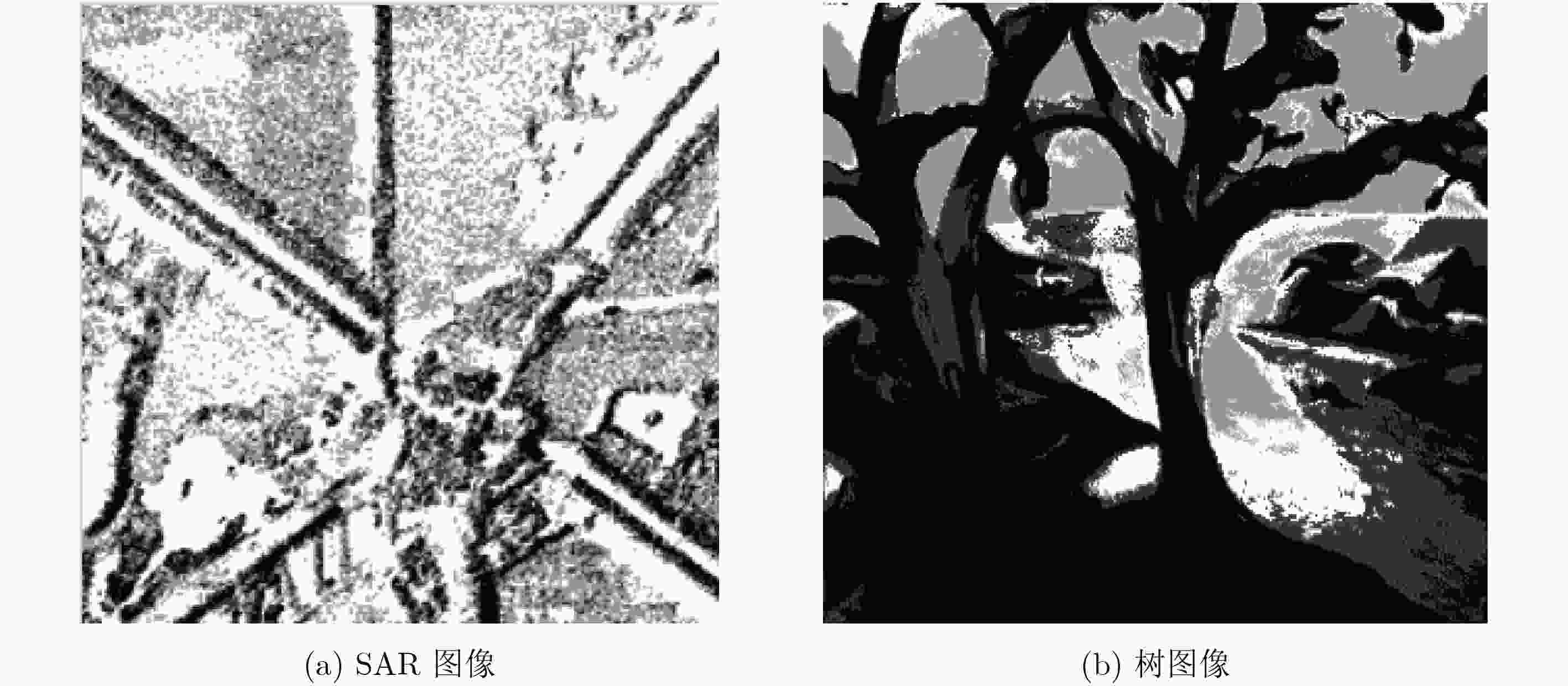
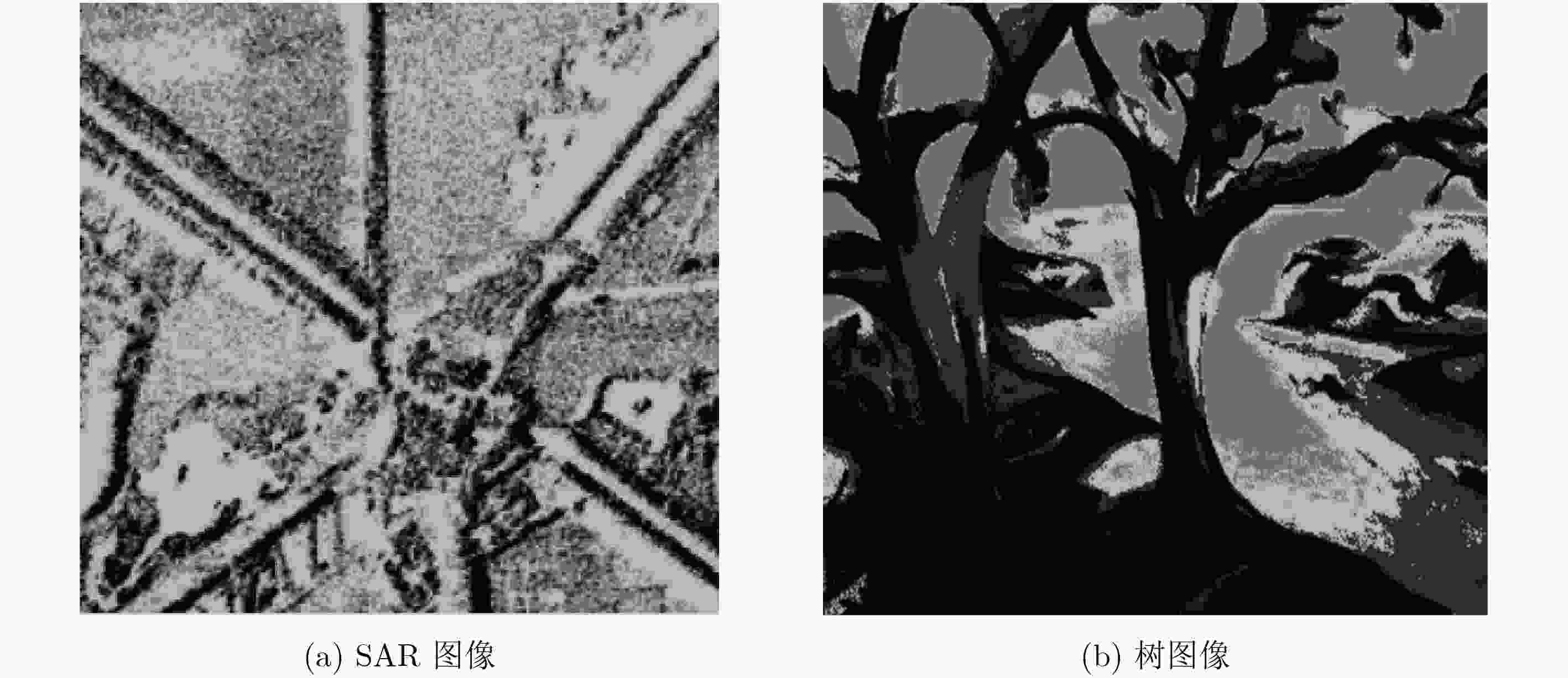
数据集	SC	STSC	AFS	本文算法
Iris	75.87	78.63	78.06	85.49
Heart	28.54	26.23	18.45	40.33
Sonar	7.32	1.83	15.47	22.38
Wine	89.30	89.34	85.67	87.96
Protein	54.43	48.24	36.62	65.80
Hepatitis	13.75	4.78	3.57	17.42
Segmentation	65.58	66.72	58.56	72.24
Pen digits	60.53	61.48	–	66.52

下载: 导出CSV

表 4 SAR图像分割性能对比表

	谱聚类算法	本文算法
运行时间(S)	30.62	3.27
误分率(%)	9.53	5.34

下载: 导出CSV

表 5 树图像分割性能对比表

	谱聚类算法	本文算法
运行时间(S)	16.39	4.25
误分率(%)	6.87	2.13

下载: 导出CSV

表 6 复杂度分析

	计算步骤	复杂度
	计算矩阵 ${{A}}$	O(n²)
	计算矩阵 ${{B}}$	O(n(N–n))
若矩阵 ${{A}}$正定	对 ${{A}}$矩阵分解	O(n³)
	求解矩阵 ${{p}}$	O(n²(N–n))
	矩阵分解	O(n³)
	求解矩阵 ${{Y}}$	O(n²N)
若矩阵 ${{A}}$非正定	求解矩阵 ${{S}}$	O(n²N)
	对矩阵 ${{S}$对角分解	O(n³)
	求解矩阵 ${{Y}}$	O(n²N)
	K-means算法进行聚类	O(nK²T)

下载: 导出CSV

参考文献(22)

JAIN A. Data clustering: a review[J]. ACM Computing Surveys, 1999, 31(3): 264–323. DOI: 10.1145/331499.331504

XU Rui. Survey of Clustering Algorithms[M]. New Jersey: IEEE Press, 2005: 645–678. doi: 10.1109/TNN.2005.845141.

RAMON-GONEN R and GELBARD R. Cluster evolution analysis: Identification and detection of similar clusters and migration patterns[J]. Expert Systems with Applications, 2017, 83: 363－378. DOI: 10.1016/j.eswa.2017.04.007.

WITTEN I H and FRANK E. Data Mining: Practical Machine Learning Tools and Techniques[M]. Massachusetts: Morgan Kaufmann, 2005: 81–82. doi: 0120884070, 9780120884070.

夏平, 任强, 吴涛, 等.融合多尺度统计信息模糊C均值聚类与Markov随机场的小波域声纳图像分割[J]. 兵工学报, 2017, 38(5): 940－948. DOI: 10.3969/j.issn.1000-1093.2017.05.014.

XIA Ping, REN Qiang, WU Tao, et al. Sonar image segmentation fusion of multi-scale statistical information FCM clustering and MRF model in wavelet domain[J]. Acta Armamentaria, 2017, 38(5): 940－948. DOI: 10.3969/j.issn.1000-1093.2017.05.014.

TREVOR H, ROBERT T, and FRIEDMAN J J H. The Elements of Statistical Learning[M]. New York: Springer, 2001: 460–514. doi: 10.1198/jasa.2004.s339.

李武, 赵娇燕, 严太山.基于平均差异度优选初始聚类中心的改进K-均值聚类算法[J]. 控制与决策, 2017, 32(4): 759－762. DOI: 10.13195/j.kzyjc.2016.0274.

LI Wu, ZHAO Jiaoyan, and YAN Taishan. Improved K-means clustering algorithm optimizing initial clustering centers based on average difference degree[J]. Control and Decision, 2017, 32(4): 759－762. DOI: 10.13195/j.kzyjc.2016.0274.

CHEN Weijie and GIGER M L. A fuzzy c-means (fcm) based algorithm for intensity inhomogeneity correction and segmentation of MR images[C]. IEEE International Symposium on Biomedical Imaging, Nano to Macro Marriott Crystal Gateway, Arlington, 2005, 2: 1307–1310. doi: 10.1109/ISBI.2004.1398786.

蔡晓妍, 戴冠中, 杨黎斌.谱聚类算法综述[J]. 计算机科学, 2008, 35(7): 14－18. DOI: 10.3969/j.issn.1002-137X.2008.07.004.

CAI Xiaoyan, DAI Guanzhong, and YANG Libin. Survey on spectral clustering algorithms[J]. Computer Science, 2008, 35(7): 14－18. DOI: 10.3969/j.issn.1002-137X.2008.07.004.

ZELNIK-MANOR L and PERONA P. Self-tuning spectral clustering[C]. Advances in Neural Information Processing Systems, Vancouver, 2004: 1601–1608.

YANG Peng, ZHU Qingsheng, and HUANG Biao. Spectral clustering with density sensitive similarity function[J]. Knowledge-Based Systems, 2011, 24(5): 621－628. DOI: 10.1016/j.knosys.2011.01.009.

JAIN A K. Data Clustering: 50 Years Beyond K-means[M]. Machine Learning and Knowledge Discovery in Databases. Springer Berlin Heidelberg, 2008: 651–666. doi: 10.1007/978-3-540-87479-9_3.

ZHU Xiatian, CHEN Change Loy, and GONG Shaogang. Constructing robust affinity graphs for spectral clustering[C]. Computer Vision and Pattern Recognition. IEEE, Ohio, 2014: 1450–1457. doi: 10.1109/CVPR.2014.188.

GONG Shaogang, CHEN Change Loy, and XIANG Tao. Security and Surveillance[M]. Visual Analysis of Humans. Springer London, 2011: 455–472. doi: 10.1007/978-0-85729-997-0_23.

PAVAN M and PELILLO M. Dominant sets and pairwise clustering[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 29(1): 167－172. DOI: 10.1109/TPAMI.2007.10.

丁世飞, 贾洪杰, 史忠植. 基于自适应采样的大数据谱聚类算法[J]. 软件学报, 2014, (9): 2037－2049. DOI: 10.13328/j.cnki.jos.004643.

DING Shifei, JIA Hongjie, and SHI Zhongzhi. Spectral clustering algorithm based on adaptive Nyström sampling for big data analysis[J]. Journal of Software, 2014, (9): 2037－2049. DOI: 10.13328/j.cnki.jos.004643.

LIU Xiaodong and REN Yan. Novel artificial intelligent techniques via AFS theory: Feature selection, concept categorization and characteristic description [J]. Applied Soft Computing, 2010, 10(3): 793－805. DOI: 10.1016/j.asoc.2009.09.009.

LIH Xiaodong, WANG Xianchang, and PEDRYCZ W. Fuzzy clustering with semantic interpretation[J]. Applied Soft Computing, 2015, 26: 21－30. DOI: 10.1016/j.asoc.2014.09.037.

BELONGIE S, FOWLKES C, FAN C, et al. Spectral partitioning with indefinite kernels using the Nyström extension[C]. European Conference on Computer Vision. Springer-Verlag, Denmark, 2002: 531–542. doi: 10.1007/3-540-47977-5_35.

WU Mingrui. A local learning approach for clustering[C]. International Conference on Neural Information Processing Systems, Hong Kong, China, 2006: 1529–1536.

STREHL A and GHOSH J. Cluster ensembles-aknowledge reuse framework for combining multiple partitions[J]. The Journal of Machine Learning Research, 2003, 3(3): 583－617. DOI: 10.1162/153244303321897735.

HU Zhaoling, GUO Dazhi, and SHENG Yehua Extracting textural in formation of satellite SAR image based on wavelet decomposition[J]. Journa1 of Remote Sensing, 2001, 5: 423－427.

施引文献

资源附件(0)

访问统计