Dynamic Pilot Allocation Scheme for Joint User Grouping and Alliance Game in Massive MIMO Systems
-
摘要:
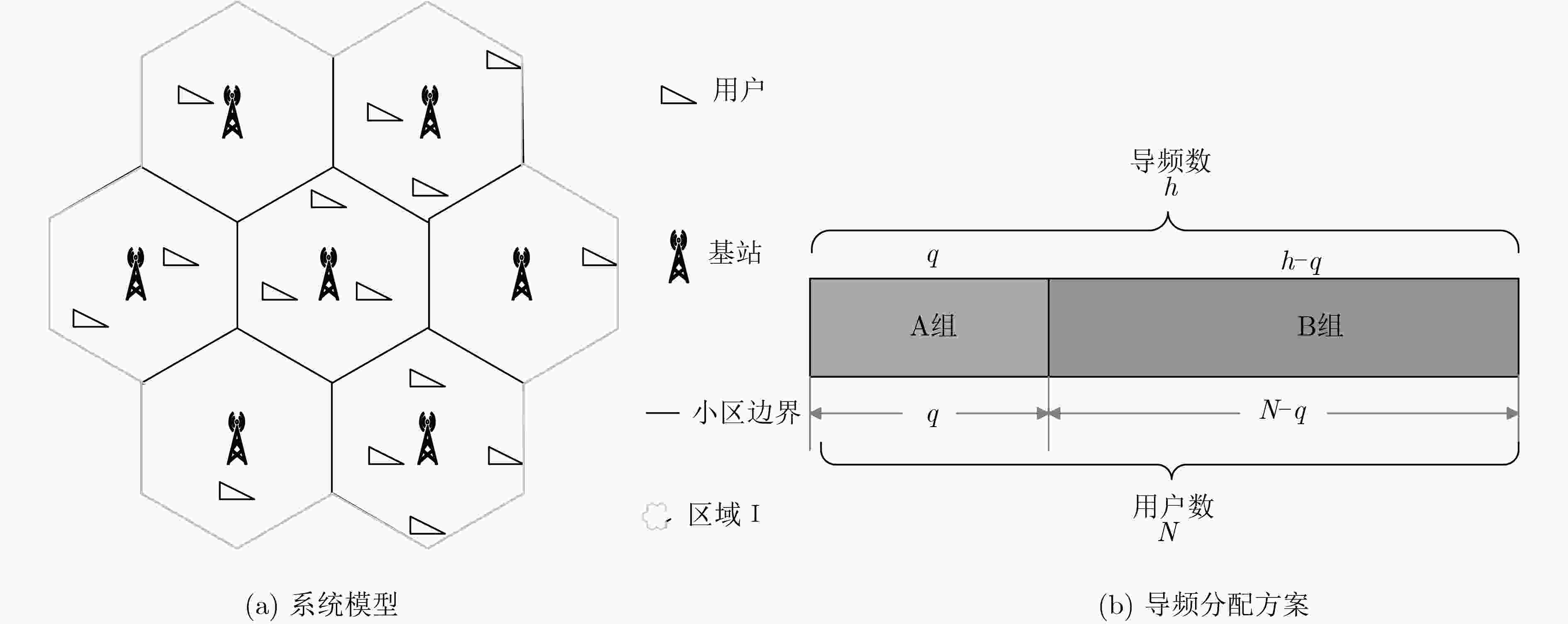
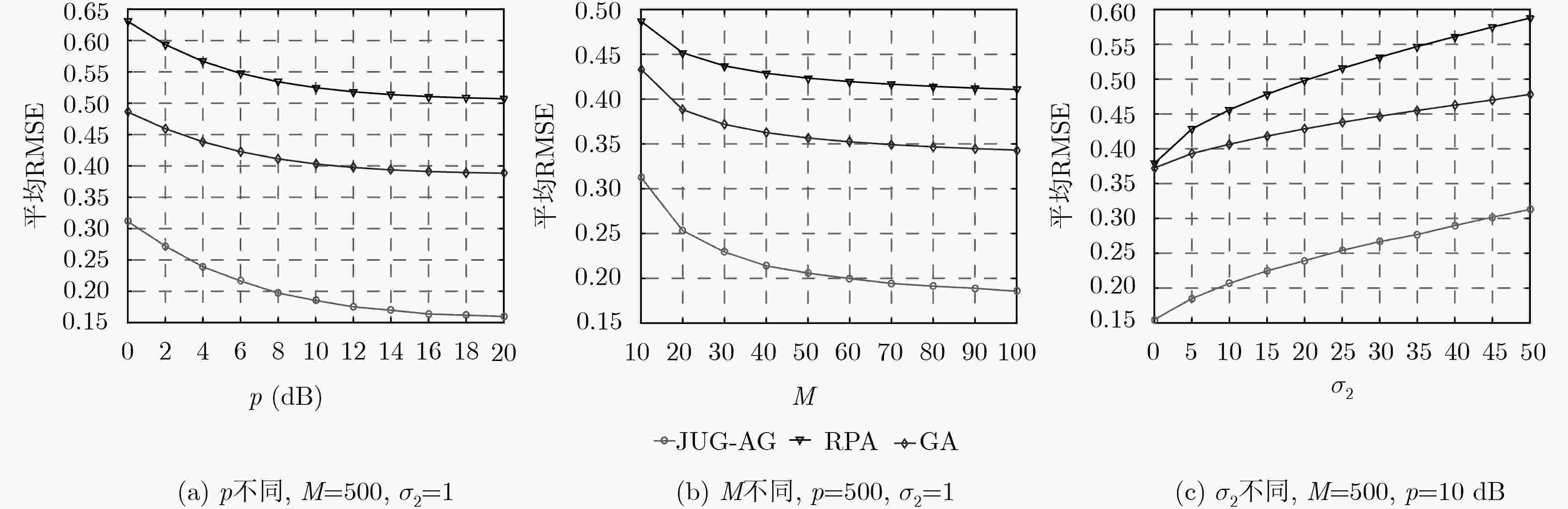
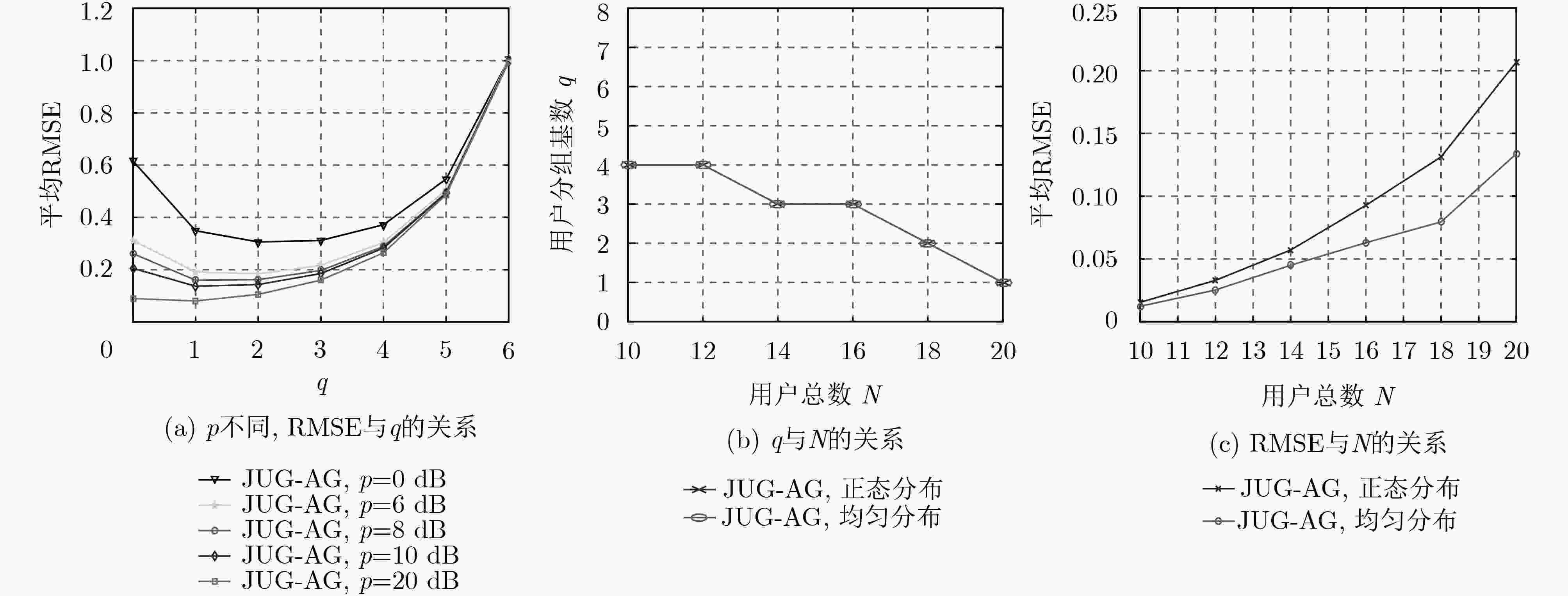
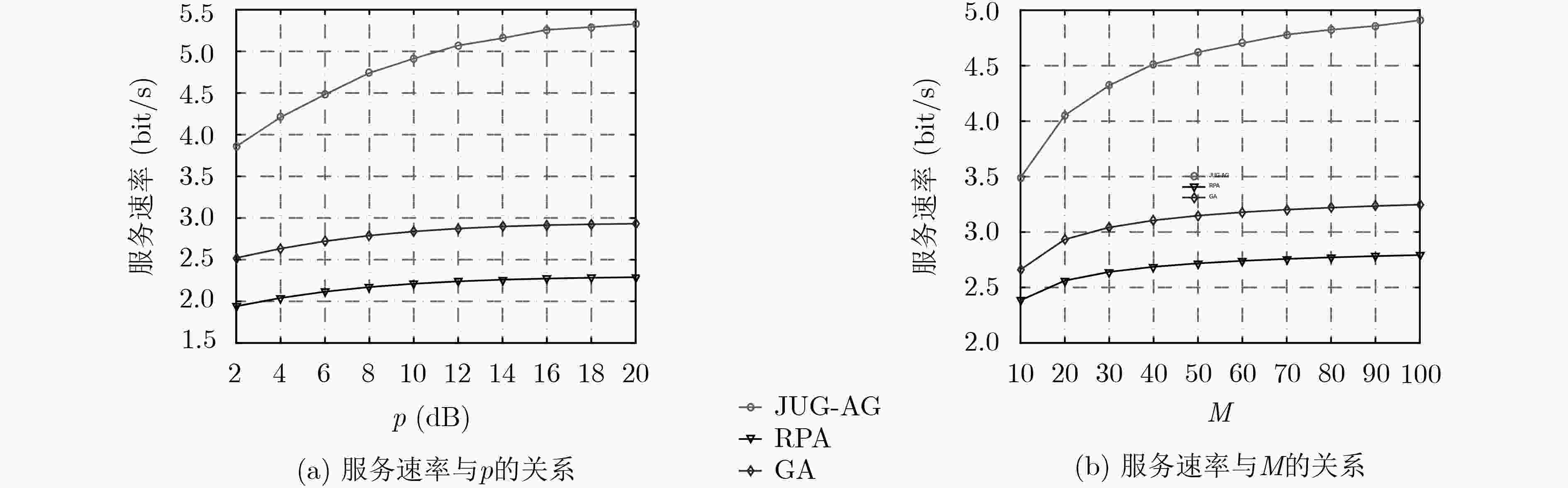
大量研究表明,大规模MIMO系统中的小区边缘用户比中心用户更易遭受导频污染的影响。因此,该文提出一种联合用户分组和联盟博弈(JUG-AG)的动态导频分配方案来减轻系统导频污染。根据用户信号强度将所有用户分为A,B两组,把接收基站信号强度弱的小区边缘用户记为A组,剩余用户则为B组。A组用户使用相互正交的导频,B组用户则借助联盟博弈来重复使用剩余的正交导频。在B组用户的联盟博弈中,用户被分成若干个互不相交的用户子联盟,属于不同子联盟的用户分配不同的相互正交导频序列,而属于同一子联盟中的用户使用相同的导频序列。与已有的导频分配方案相比,该文提出的JUG-AG方案更灵活,可以用于所有用户随机分布的场景。而且,该算法通过循环搜索可以获得整体最优解。仿真结果表明JUG-AG方案能够有效降低上行链路中用户信号检测的平均均方根误差(RMSE),而且可以提高用户的平均服务速率。
-
关键词:
- 大规模多输入多输出 /
- 导频污染 /
- 均方根误差 /
- 服务速率 /
- 联合用户分组和联盟博弈
Abstract:Many researches demonstrate that cell-edge users are more susceptible to pilot contamination than the cell-center users in massive MIMO systems. Therefore, this paper proposes a dynamic pilot allocation scheme called Joint User Grouping and Alliance Game (JUG-AG) to mitigate pilot contamination. According to the user signal strength, the users are divided into two groups, namely A and B. Users with weak strength of received Base Stations (BSs) signals are recorded as group A, and the remaining users are group B. The users of group A use mutually orthogonal pilots, and the users of group B reuse the remaining orthogonal pilots by means of alliance game. In the alliance game for the users of group B, users are divided into several disjoint user sub-alliances, users belonging to different sub-alliances are allocated different orthogonal pilot sequences, and users in the same sub-alliance reuse the same pilot sequence. Compared with the existing pilot allocation schemes, the proposed JUG-AG scheme is more flexible and can be used for scenarios that all users are randomly distributed. Moreover, the algorithm can obtain the overall optimal solution through cyclic searching. The simulation results demonstrate that the JUG-AG scheme can effectively reduce the average Root Mean Square Error (RMSE) of user signal detection in the uplink and improve the average service rate of users.
-
算法1 导频分配算法 步骤 1 (用户分组):计算所有用户的${\eta _{iik}}$值,从小到大排序。
根据排序,优选前$q$个值较小的用户为A组,剩余($N - q$)个用户为B组。步骤 2 (联盟博弈): 初始化:对于B组用户,给定初始联盟结构$\lambda = \{ {\lambda _1},{\lambda _2}, ···, {\lambda _{h - q}}\} $,并设当前搜索次数$\zeta = 0$。 循环: (1) 对于所有用户$(i,k) \in \varPhi \,\,$(即B用户),进行循环搜索; (2) 对于所有${\lambda _j} \in \{ \{ {\lambda _1},{\lambda _2}, ···, {\lambda _{h - q}}{{\rm \} \backslash }}\Gamma (i,k)\} ,(j = 1,2,···,$ $h - q)$,进行查找: 效用函数为RMSE时,若联盟调整规则1中两个条件都满足,则
有$\lambda {{\rm = }}\lambda ^0$。同理,效用函数为服务速率时,若联盟调整规则2中两
个条件都满足,则有$\lambda {{\rm = }}\lambda ^0$。否则,联盟结构保持不变($\lambda {{\rm = }}\lambda $)。 结束(对应循环2) 搜索次数增加,即$\zeta = \zeta + 1$, 结束(对应循环1) 直到$\lambda \xrightarrow{{(i,k)}}\, \,{\lambda ^0}$的所有条件不成立或$\zeta > \varpi $,循环结束。 步骤 3 (导频分配):A组用户分配$q$个正交导频,B组中($N - q$)个用户根据第2步用户子联盟分配的结果将剩余$h - q$个正交导频依次分配给这$h - q$个用户子联盟。 表 1 仿真参数设置
参数 数值 参数 数值 基站坐标(km) (4.0,4.0), (5.7,4.0),
(2.3,4.0), (4.9,5.5),
(3.1,5.5), (4.9,2.5),
(3.1,2.5)最大搜索次数$\varpi $ 800 小区数L 7 路径衰落因子$\upsilon $ 3 用户数N 20 导频数h 8 -
ZHANG Ruoyu, ZHAO Honglin, ZHANG Jiayan, et al. Hybrid orthogonal and non-orthogonal pilot distribution based channel estimation in massive MIMO system[J]. Journal of Systems Engineering and Electronics, 2018, 29(5): 881–898. doi: 10.21629/JSEE.2018.05.01 KIM K, LEE J, and CHOI J. Deep learning based pilot allocation scheme (DL-PAS) for 5G massive MIMO system[J]. IEEE Communications Letters, 2018, 22(4): 828–831. doi: 10.1109/LCOMM.2018.2803054 ZHI Hui and HU Yanjun. Novel multi-cell precoding schemes for TDD massive MIMO systems[J]. Wireless Personal Communications, 2017, 97(4): 6111–6129. doi: 10.1007/s11277-017-4829-4 ZHU Xudong, WANG Zhaocheng, QIAN Chen, et al. Soft pilot reuse and multicell block diagonalization precoding for massive MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(5): 3285–3298. doi: 10.1109/TVT.2015.2445795 张进彦, 金凤, 尹礼欣. 大规模MIMO系统中基于用户分类的动态导频分配[J]. 电信科学, 2017, 33(9): 76–84. doi: 10.11959/j.issn.1000-0801.2017212ZHANG Jinyan, JIN Feng, and YIN Lixin. Dynamic pilot assignment in massive MIMO system based on user classification[J]. Telecommunications Science, 2017, 33(9): 76–84. doi: 10.11959/j.issn.1000-0801.2017212 ZHU Xudong, WANG Zhaocheng, DAI Linglong, et al. Smart pilot assignment for massive MIMO[J]. IEEE Communications Letters, 2015, 19(9): 1644–1647. doi: 10.1109/LCOMM.2015.2409176 KU Li, FAN Jiancun, and DENG Jianguo. Low complexity pilot allocation in massive MIMO systems[C]. The 8th IEEE International Conference on Communication Software and Networks, Beijing, China, 2016: 402–406. AKBAR N, YANG Nan, SADEGHI P, et al. Multi-cell multiuser massive MIMO networks: User capacity analysis and pilot design[J]. IEEE Transactions on Communications, 2016, 64(12): 5064–5077. doi: 10.1109/TCOMM.2016.2614674 JING Xiaorong, LI Mengwan, LIU Hongqing, et al. Superimposed pilot optimization design and channel estimation for multiuser massive MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(12): 11818–11832. doi: 10.1109/TVT.2018.2875480 CASTAÑEDA GARCIA M H and LUO Jian. Time-shifted pilots multiplexed with uplink data and unequal power allocation[C]. 2018 IEEE Wireless Communications and Networking Conference, Barcelona, Spain, 2018: 1–6. GAO Hongyuan, SU Yumeng, ZHANG Shibo, et al. Antenna selection and power allocation design for 5G massive MIMO uplink networks[J]. China Communications, 2019, 16(4): 1–15. GUO Kaifeng, GUO Yan, and ASCHEID G. Energy-efficient uplink power allocation in multi-cell mu-massive-MIMO systems[C]. The 21th European Wireless Conference, Budapest, Hungary, 2015: 1–5. AHMADI H, FARHANG A, MARCHETTI N, et al. A game theoretic approach for pilot contamination avoidance in massive MIMO[J]. IEEE Wireless Communications Letters, 2016, 5(1): 12–15. doi: 10.1109/LWC.2015.2487261 MOCHAOURAB R, BJÖRNSON E, and BENGTSSON M. Adaptive pilot clustering in heterogeneous massive MIMO networks[J]. IEEE Transactions on Wireless Communications, 2016, 15(8): 5555–5568. doi: 10.1109/TWC.2016.2561289 BOGOMOLNAIA A and JACKSON M O. The stability of hedonic coalition structures[J]. Games and Economic Behavior, 2002, 38(2): 201–230. doi: 10.1006/game.2001.0877 OSBORNE M J and RUBINSTEIN A. A Course in Game Theory[M]. Cambridge, USA: MIT Press, 1994: 255–298. -





 下载:
下载:











 下载:
下载:
