Deployment Algorithm of Service Function Chain Based on Transfer Actor-Critic Learning

1.   引言

网络切片是指将一个完整的物理网络切割成为多个独立的适用不同应用场景的逻辑虚拟网络。每个切片网络包含有若干条相同服务类型的服务功能链(Service Function Chain, SFC)，每条SFC由若干有序虚拟网络功能(Virtual Network Function, VNF)组成。系统需要根据用户需求和相关约束，合理地将VNF放置在底层网络并为其分配CPU、内存、带宽等物理资源^[1]。

目前，大多数研究都是以成本最小化为目标，将端到端时延作为约束条件。文献[2]旨在最小化运营成本中的激活、能耗和传输成本，得到VNF部署和路由分配优化方案。文献[3]考虑时变工作负载和实例化VNF的基本资源消耗，以优化资源利用率。文献[4]和文献[5]都提出了时延感知的优化算法来保证端到端时延，但是把各类时延设为固定值，与资源分配无关。文献[6]针对核心网切片的SFC部署，最大限度减少VNF调度时延，使得运营商能够服务更多用户。首先，上述文献的方案只针对核心网切片，无法直接支持在基于集中式单元/分布式单元(Centralized Unit/Distributed Unit, CU/DU)的两级云无线接入网(Cloud-Radio Access Network, C-RAN)架构下的SFC部署^[7]。其次，这些方案忽略了实际网络中动态随机变化的业务到达和队列积压情况，如果不及时针对当前环境进行方案调整，系统端到端时延会显著增加。此外，上述算法均只针对某一特定的网络参数配置，即SFC数目、业务数据包到达率等设置固定，一旦这些参数发生变化，其求解策略将无法适应新网络，需要对算法本身进行调整。

针对上述问题，本文提出了一种基于迁移演员-评论家算法(Transfer Actor-Critic Algorithm, TACA)的面向时延优化的接入网切片SFC部署方案。主要贡献包括：

(1) 考虑采用基于CU/DU的两级C-RAN架构，以最小化系统端到端时延为目标，建立排队时延、节点处理时延及链路传输时延与VNF放置和资源分配的关联性；

(2) 考虑环境中SFC业务请求数据包到达的随机性和队列长度的动态性，将SFC的部署问题建立为马尔可夫决策过程(Markov Decision Process, MDP)，并通过A-C算法不断与环境进行交互实现SFC部署策略的动态调整；

(3) 考虑一个系统在不同时段SFC的部署任务不尽相同，如在目标任务中需部署SFC条数较少但业务数据包到达率更高。为了降低针对目标任务模型的训练成本，提高学习的效果，在传统A-C学习中引入迁移学习的思想，实现利用源任务中的部署知识来学习新的部署策略。

2.   系统模型

2.1   系统场景

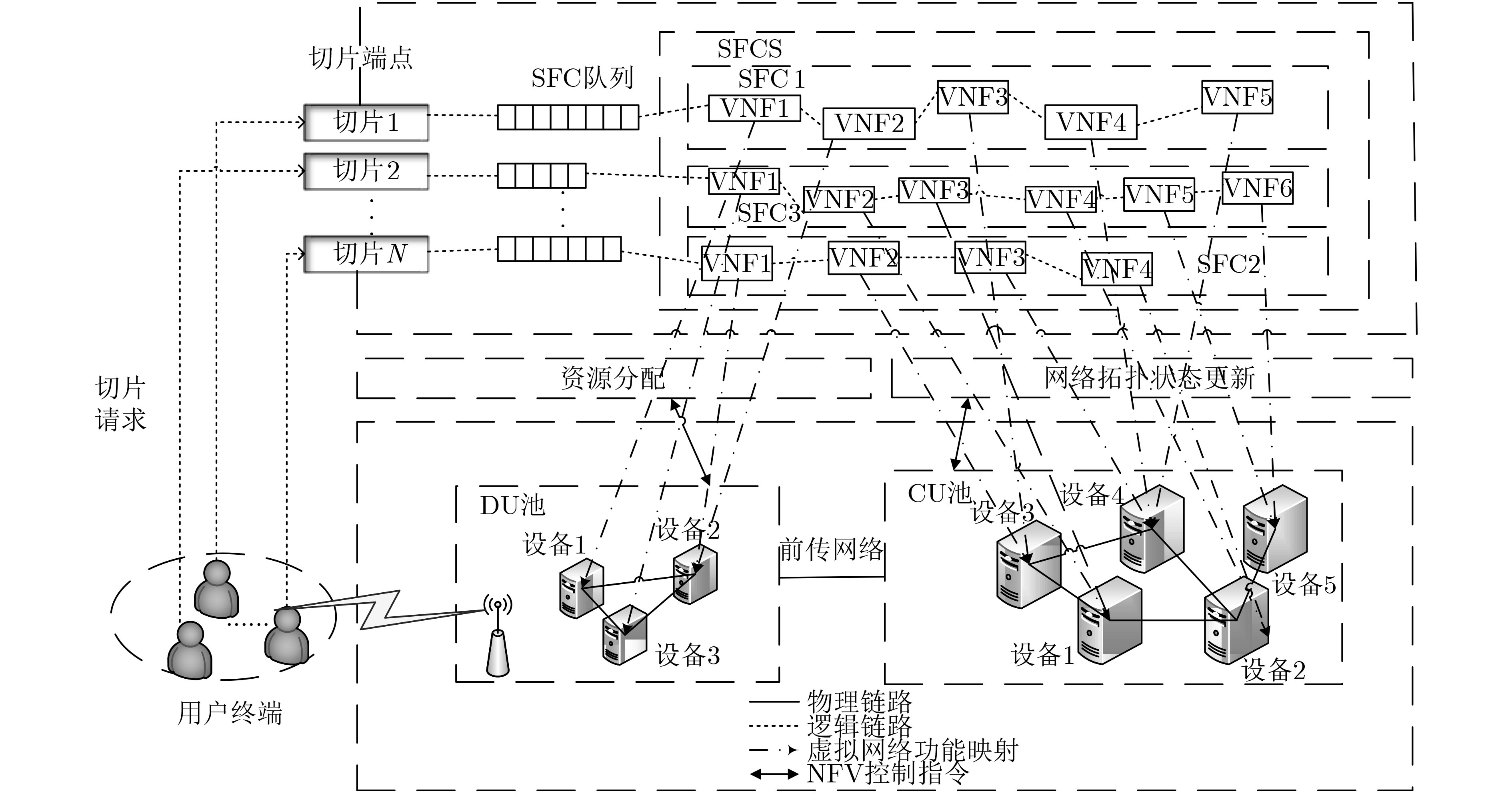
图1所示为基于5G C-RAN上行条件的SFC部署的系统架构图。首先，网络中的各协议层功能在通用设备被虚拟化为不同的VNF，共享基础设施资源。其次，该架构采用DU和CU独立部署的方式，DU池和CU池之间通过下一代前传网络接口(Next Generation Fronthaul Interface, NGFI)进行数据传输。

图  1  系统架构

下载: 全尺寸图片 幻灯片

在5G C-RAN上行链路中，3GPP总结了8种接入网切片的VNF放置方式。切片一旦选择某种VNF放置方式，即意味着SFC部署在CU池和DU池的VNF数量确定，基于此，再进行VNF放置节点的选择以及池内计算资源和链路资源分配。此外，不同的VNF放置方式对SFC的最大可容忍NGFI传输时延要求不同，因此放置方式还会影响SFC的NGFI带宽资源分配。本文中将接入网切片的VNF放置和资源分配方式统称为SFC部署策略。

2.2   物理网络模型

用带权无向图$G = {\rm{\{ }}N,L{\rm{\} }}$来表示基础设施网络，$N = {N_{\rm{D}}} \cup {N_{\rm{C}}} = \{ {n_1},{n_2},···,{n_U}\}$为设备节点集，由DU池节点集${N_{\rm{D}}}$与CU池节点集${N_{\rm{C}}}$组成。$L = {L_{\rm{D}}} \cup$${L_{\rm{C}}} \cup {L_{\rm{N}}} = {\rm{\{ }}{l_1},{l_2}, ··· ,{l_V}{\rm{\} }}$代表物理链路集$L$，由DU池链路集${L_{\rm{D}}}$、CU池链路集${L_{\rm{C}}}$和前传网络${L_{{\rm{NGFI}}}}$构成。服务器节点${n_u}$的计算资源容量为${C_{{n_u}}}$，链路${l_v}$的带宽资源容量为${B_{{l_v}}}$, ${l_v}.{\rm head}$和${l_v}.{\rm tail}$代表连接${l_v}$的两个相邻物理节点。此外，系统中的切片集合为$K$，${M_k}$代表切片$k$中的SFC集合。最后，考虑切片请求数据可以在DU池侧进行缓存。切片$k$的SFC$m$在时隙$t$的队列长度为${q_{k,m}}(t)$，并满足$0 \le {q_{k,m}}(t) \le {q_{\max }}, \forall t$，其中${q_{\max }}$代表最大队列长度。

2.3   问题描述

本文将系统的时间维度分为若干个时隙，用$\varGamma {\rm{ = }}\{ 1,2, ··· ,t, ··· ,T\}$表示时隙集合，${T_s}$为每个时隙$t$的持续时间。假设切片$k$的SFC$m$的数据包到达过程为服从时变参数为${\lambda _{m,k}}(t)$的泊松分布，数据包的大小服从均值为${\overline p _{m,k}}$的指数分布^[8]。令${a_{{\rm{op}}}}(t) =$$\{ {{\rm{op}}_k}(t)|k \in K\}$表示切片$k$在时隙$t$所选VNF放置方式，其中${{\rm{op}}_k}(t) \in \varOmega$, $\varOmega$表示8种接入网VNF放置方式集合。而后根据放置方式分别为DU池、CU池的各个VNF进行资源分配。

首先，假定每台设备包含有多个CPU，单个CPU的计算能力为${C_{{\rm{cpu}}}}$(CPU cycles/s)^[9]。令$\alpha _{k,m}^c(t) =$$\left\{ x_{{n_u}}^{f_{m,k}^j} \cdot c_{{n_u}}^{f_{m,k}^j}|j \in {F_{m,k}},{n_u} \in N_{f_{m,k}^j}^{'}\right\}$代表时隙$t$切片$k$的SFC$m$的计算资源分配方式。其中，${F_{m,k}}$是切片$k$的SFC$m$的VNF集合，$N_{f_{m,k}^j}^{'}$代表第$j$个VNF可以实例化的物理节点集合。$x_{{n_u}}^{f_{m,k}^j}{\rm{ = }}1$代表切片$k$的SFC$m$的第$j$个VNF放置在物理节点${n_u}$上，$c_{{n_u}}^{f_{m,k}^j}$代表第$j$个VNF所分配的计算资源。令${J_{k,m}} =$$({a_{k,m}}(t),{w_{k,m}}(t))$切片$k$的SFC$m$的计算处理任务，其中${a_{k,m}}(t)$为时隙$t$到达的数据包个数，${w_{k,m}}(t)$为完成该项任务所需的CPU周期。不同类型切片的SFC任务处理单位比特数据所需的CPU周期也存在差异^[10,11]，设为${x_k}$，则有${w_{k,m}}(t) = {a_{k,m}}(t){\overline { \cdot p} _{k,m}} \cdot {x_k}$，因此物理节点处理时延为

然后，令$\alpha _{k,m}^b(t) \!=\! \left\{\! y_{{l_v}}^{f_{m,k}^j} \cdot b_{{l_v}}^{f_{m,k}^j}|j \in F_{m,k}^{'},{l_v} \in L \!\right\}$代表切片$k$的SFC$m$在时隙$t$的物理链路带宽资源分配方式。其中，$y_{{l_v}}^{f_{m,k}^j} = 1$代表切片$k$的SFC$m$的第$j$个VNF映射到链路${l_v}$上向下一个VNF发送数据, $b_{{l_v}}^{f_{m,k}^j}$代表SFC $m$的第$j$个VNF在链路${l_v}$分配的带宽资源，$F_{m,k}^{'}$代表不包括DU池和CU池末端VNF的集合。$b_{{\rm{NG}}}^{{f_{m,k}}}(t)$表示NGFI为其分配的带宽资源。因此，链路传输时延为

最后，令${r_{k,m}}(t)$表示切片$k$的SFC$m$在时隙$t$内的服务速率。本文模型考虑的是上行协议功能的处理，因此每条SFC的第1个VNF的数据处理速率就是该条链路的服务速率^[12]，即有${r_{k,m}} = c_{{n_u}}^{f_{m,k}^1}(t)/{x_k}$，因此平均包处理速率为${v_{k,m}}(t) = {r_{k,m}}(t)/{\overline p _{k,m}}$。令${q_{k,m}}(t)$代表在时隙$t$切片$k$的SFC$m$的队列长度，SFC在DU侧的队列更新公式为${q_{k,m}}(t + 1) =$$\max \{ {q_{k,m}}(t) + {a_{k,m}}(t) - {d_{k,m}}(t),0\}$。其中，${d_{k,m}}(t) =$${v_{k,m}}(t) \cdot {T_s}$代表在时隙$t$内处理的数据包数目。此外为了保证队列不溢出，还需满足${r_{k,m}}(t) \ge$$\dfrac{{{q_{k,m}}(t) + {a_{k,m}}(t) - {q_{\max }}}}{{{T_s}}}$。根据Little定理，SFC的排队时延为

从而时隙$t$部署切片的时延为$\tau (t) = {\tau _1}(t) +$${\tau _2}(t) + {\tau _3}(t)$，因此，传输切片的总平均系统端到端时延为

本文的接入网切片SFC部署问题可建立为基于VNF放置选择、计算资源、链路带宽资源和NGFI带宽资源联合分配的时延最小化数学模型

上述约束条件中，C1表示任意物理节点上的计算资源限制。C2和C3分别代表任意物理链路和NGFI上的带宽资源限制。C4确保任意VNF只能实例化在一个物理节点上。C5确保任意VNF至多只能选择一条链路发送数据。C6和C7代表SFC上相邻的两个VNF若部署在不同的物理节点上，则这两个节点必须相邻。C8和C9分别代表只有当SFC的虚拟节点映射到物理节点、虚拟链路映射到物理链路时，才分配计算资源和带宽资源。

3.   基于A-C学习的SFC部署方案

3.1   MDP

上述VNF放置以及资源分配过程可以建立为一个具有连续状态和动作空间的离散时间MDP^[13]。MDP定义为一个多元组$M = < {\cal{S}},{\cal{A}},{\rm{\mathcal{P}}},{\cal{R}} >$，其中${\cal{S}}$是状态空间，${\cal{A}}$是动作空间，${\rm{\mathcal{P}}}$是转移概率，${\cal{R}}$是奖励函数。${s^{(t)}} \in {\cal{S}}$为时隙$t$的系统状态，由所有切片的全部SFC的队列长度以及其数据包到达率共同决定。动作${a^{(t)}} \in {\cal{A}}$为VNF放置和计算资源、链路带宽资源和NGFI带宽资源分配情况。在状态${s^{(t)}}$执行动作${a^{(t)}}$后，即完成当前时隙的SFC部署，系统会得到一个立即回报${R_t} = - \tau (t)$。

由于本文动作空间也连续，因此假设动作${a^{(t)}}$来自于一个随机策略$\pi (a|s) = \Pr ({a^{(t)}} = a|{s^{(t)}} = s)$，代表在状态${s^{(t)}}$下采取动作${a^{(t)}}$转移至${s^{(t + 1)}}$的概率，即意味着当环境处于某个队列长度和数据包到达率状态时，系统能够根据学习策略选择特定的VNF放置方式和资源分配方案。

解决MDP的许多方法都依赖于环境动态变化的先验知识，然而要提前精确获知未来的队列长度和数据包到达率很困难，因此本文采用无需先验知识的A-C学习方法来解决MDP问题。在A-C学习中，状态-动作值函数$Q$表示从当前状态开始并采取动作，然后再根据给定策略选择下一个动作的累积奖励期望值

其中，$\beta \in (0,1)$是衡量当前或未来决策的折扣因子，${\rm{E}}\{ \cdot \}$表示期望。

A-C学习的目标是寻找一个策略$\pi$，最大化式(7)所示的目标函数

其中，${d^{\pi} }(s)$是在策略$\pi$下的稳定状态分布，假设其存在且独立于初始状态${s_0}$。

3.2   SFC部署的A-C学习框架

A-C学习算法结合了强化学习中的策略方案和值函数方案，能够在连续动作空间中有效学习随机策略，并获得较好的收敛性^[14]。算法框架如图2(a)所示。其中演员定义随机参数化策略并根据环境中的队列长度和数据包到达情况生成SFC部署动作。而后评论家根据执行部署动作后获得的时延奖励对当前策略进行评判，并通过时间差分(Time Difference, TD)误差更新值函数。在评论家部分完成值函数近似和参数更新后，演员使用评论家的输出更新其策略，以选择所获奖励更多的动作。

图  2  A-C学习框架

下载: 全尺寸图片 幻灯片

3.2.1   演员过程

在演员阶段，首先采用向量${{\theta}} = {({\theta _1},{\theta _2}, ··· ,{\theta _n})^{\rm{T}}}$生成参数化的部署策略${\pi _\theta }(s,a) = \Pr (a|s,\theta )$，再采用策略梯度的方法逐步对策略参数进行改进。目标函数$J({\pi _\theta })$的局部最大值可以通过梯度上升法得到，则对${{\theta}}$的策略梯度更新表示为

其中，${\varepsilon _{a,t}} > 0$是策略更新的学习率。策略梯度的计算为

采用高斯分布^[15]构造动作选择的随机策略，参数化策略写为${{\pi} _\theta }(s,a) = \dfrac{1}{{\sqrt {2\pi } \sigma }}\exp \left( - \dfrac{{{{(a - \mu (s))}^2}}}{{2{\sigma ^2}}}\right)$，其中，$\mu (s)$是该状态下确定动作的均值，$\sigma$是对所有动作探索程度的标准差。且有$\mu (s) = {{{\theta}} ^{\rm{T}}} \times {{{Z}}}(s) =$$\displaystyle\sum\nolimits_{j = 1}^n {{\theta _j}{z_j}(s)}$，其中，${ Z}(s) = {({z_1}(s),{z_2}(s), ··· {z_n}(s))^{\rm{T}} }$是状态$s$的基函数向量。参数${{\theta}}$可以通过常规策略梯度方法进行更新。由于在本文中，将队列长度和数据包到达率作为特征，因此，$n = 2 \times \displaystyle\sum\nolimits_{k = 1}^K {{M_k}}$，且${ Z}(s)$写为

3.2.2   评论家过程

评论家部分具有评估策略优劣的能力。由于本文中状态和动作空间无限，${Q^{\pi} }(s,a)$不能通过Bellman方程进行迭代计算得到，需要采用函数近似来估计值函数并通过一些样本来更新参数。状态-动作值函数采用参数向量${{\omega}} = {({\omega _1},{\omega _2},··· ,{\omega _n})^{\rm{T}}}$进行近似参数化，即${Q_\omega }(s,a) \approx {Q^{\pi} }(s,a)$。基于特征的线性函数近似器具有较低复杂度，而且能保证学习算法的收敛性和稳定性，鉴于此，本文将其作为值函数近似器，即

其中，${{\varPsi}} (s,a) = {({\psi _1}(s,a),{\psi _2}(s,a), ··· ,{\psi _n}(s,a))^{\rm{T}}}$称为状态$s$下采取动作$a$的特征向量。

而后，给出状态转移样本$({s^{(t)}},{a^{(t)}},{R_{t + 1}},{s^{(t + 1)}},$${a^{(t + 1)}})$和值函数的近似表达式，则TD误差为

采用梯度下降法近似真实值函数，并在梯度方向上不断更新近似值。由于采用线性函数近似器，${\varepsilon _{c,t}} > 0$是值函数估计的学习率，可得参数${{\omega}}$的更新方式为

3.2.3   A-C算法执行过程

式(9)所示的策略梯度公式表明了演员过程(策略梯度${{\text{∇}} _\theta }J({\pi _\theta })$)与评论家过程(状态-动作值函数${Q^{{\pi _\theta }}}(s,a)$)之间的关系。评论家利用式(11)定义的近似状态-动作值函数${Q_\omega }(s,a)$来评估策略性能。因此，演员过程遵循近似策略梯度${{\text{∇}} _\theta }J({\pi _\theta }) \approx$$\displaystyle\int_{\cal{S}} {{d^{\pi} }(s)\displaystyle\int_{\cal{A}} {{{\text{∇}} _\theta }{\pi _\theta }(s,a){Q_\omega }} } (s,a){\rm{d}}a{\rm{d}}s$，该式中，${{\text{∇}} _\theta }{\pi _\theta }(s,a) = {\pi _\theta }(s,a){{\text{∇}} _\theta }\ln {\pi _\theta }(s,a)$。又由于高斯分布是指数函数，可得

采用策略梯度近似可能会引起一定偏差，因此不能保证采用该有偏差的策略梯度能够找到最优解。为了避免偏差实现精确策略梯度，需要对值函数近似值采用相容特征并最小化误差，其中相容特征满足${{\text{∇}}_\omega }{Q_\omega }(s,a) = {{\text{∇}} _\theta }\ln {\pi _\theta }(s,a)$，则${Q^{{\pi _\theta }}}(s,a)$最接近的近似值${Q_\omega }(s,a)$是无偏的。

由于本文采用线性近似器，即${Q_\omega }(s,a) = {\omega ^{\rm{T}}} \cdot {{\varPsi}}$$(s,a)$，代入相容特征公式，则有

根据相容特征公式，可得值函数${Q^{{\pi _\theta }}}(s,a)$相容函数近似为${Q_\omega }(s,a) = {\omega ^{\rm{T}}} \cdot {\nabla _\theta }\ln {\pi _\theta }(s,a)$，又因为${\pi _\theta }(s,a) \sim N(\mu (s),{\sigma ^2})$，可得状态-动作值函数近似表达为${Q_\omega }(s,a) = {{{\omega}} ^{\rm{T}}} \cdot \dfrac{{(a - \mu (s)) \cdot { Z}(s)}}{{{\sigma ^2}}}$。

但是，采用相容近似的梯度策略梯度法仍然存在方差较大的问题。为了有效降低梯度计算中的方差，进一步提高评论家函数近似精度，引入优势函数$A(s,a) = {Q_\omega }(s,a) - {V^{\pi} }(s)$替代${Q_\omega }(s,a)$, ${V^{\pi }}(s)$为状态值函数。

同理，需采用线性函数近似器对状态值函数进行估计${V_\upsilon }(s) \approx {V^{\pi} }(s)$，即

状态值函数参数向量的更新过程类似于状态-动作值函数，即

4.   迁移A-C学习算法

在本节中，为了实现并加速该A-C学习算法在其他相似环境和学习任务中的收敛过程，考虑利用源任务学习到的SFC部署知识来寻找目标任务中时延最优的SFC部署策略。当学习过程收敛时，在特定状态下选择特定动作的机率比其他动作大得多，但这样的一个学习策略是适应当前环境和部署任务的，现在考虑将该部署策略的参数知识${{\theta}} = {({\theta _1},{\theta _2}, ···,{\theta _n})^{\rm{T}}}$迁移到其他相似目标学习任务上，使得目标任务能够较快收敛而不是从零开始学习^[16,17]。基于迁移学习的思想，本文提出了一种新的策略更新方法，如图2(b)所示的迁移A-C算法(Transfer Actor-Critic Algorithm, TACA)。

在TACA中，整体策略$\pi _\theta ^o(s,a)$分为本地策略$\pi _\theta ^n(s,a)$和外来策略$\pi _\theta ^e(s,a)$，其更新方式为

其中，$\pi _\theta ^{o(t + 1)}({s^{(t)}},a) = \pi _\theta ^{o(t)}({s^{(t)}},a),\;\forall a \in {{{\cal A}}}, \;a \ne {a^{(t)}}$。$\zeta (t) = {\ell ^t}$为迁移率，$\ell \in (0,1)$为迁移率因子，即有当$t \to \infty$, $\zeta (t) \to 0$。最后，将上述过程总结在表1的算法中。

表  1  基于迁移A-C学习的SFC部署算法

输入：高斯策略${ {\pi} _\theta }(s,a)\sim N(\mu (s),{\sigma ^2})$，以及其梯度${{\text{∇}} _\theta }\ln { {\pi} _\theta }(s,a)$，状态分布${d^{\pi} }(s)$，学习率${\varepsilon _{a,t}}$和${\varepsilon _{c,t}}$，折扣因子$\beta$
(1) for ${\rm{epsoide } }= 0,1,2, ··· ,E{p_{\max} }$ do
(2) 初始化：策略参数向量${{{\theta }}_t}$，状态-动作值函数参数向量${\omega _t}$，状态值函数参数向量${{{\upsilon}} _t}$，初始状态${s_0}\sim{d_{\pi} }(s)$，本地部署策略${\pi} _\theta ^n(s,a)$，外 　　 来迁移部署策略${\pi} _\theta ^e(s,a)$
(3) for 回合每一步$t = 0,1, ··· ,T$do
(4) 由式(20)得到整体部署策略，遵循整体策略${ {\pi} _\theta }(s,a)$选择动作${a^{(t)}}$，进行VNF放置和资源分配，而后更新环境状态${s^{(t + 1)}}$，并得到立即 　　 奖励${R_t} = - \tau (t)$
(5) end for
(6) 评论家过程：
(a) 计算相容特征：由式(10)得处于状态$s$的基函数向量，结合式(14)，式(15)得相容特征
(b) 相容近似：由式(11)得状态-动作值函数近似，由式(16)得状态值函数近似
(c) TD误差计算：由式(12)，式(17)分别得状态-动作值函数、状态值函数的TD误差
(d) 更新评论家参数：由式(13)得状态-动作值函数参数向量更新，由式(18)得状态值函数参数向量更新
(7) 演员过程：
(a) 计算优势函数
(b) 重写策略梯度：代入优势函数由式(19)得策略梯度
(c) 更新演员参数：由式(8)得策略参数向量更新
(8) end for

下载: 导出CSV 

| 显示表格

5.   仿真与性能分析

为了评估本文模型与算法的有效性，利用Tensorflow和Matlab工具进行了仿真。假设有3个不同服务规模的接入网切片，数据包到达服从泊松分布且到达率分别为：${\lambda _{1,m}}(t) \in \left[ {40,55} \right]$, ${\lambda _{2,m}}(t) \in$$\left[ {50,65} \right]$, ${\lambda _{3,m}}(t) \in \left[ {60,85} \right]$。数据包大小均值为$\overline p = 500\; {\rm{kbit}}$，最大队列长度为30个数据包。此外，3个切片处理单位比特数据所需CPU cycles分别为：${x_1}{\rm{ = }}5900$, ${x_2}{\rm{ = 6400}}$, ${x_3}{\rm{ = 7000}}$。SFC总数量取值为$\left[ {10,50} \right]$，各个切片的SFC数量比例为2:3:5，且同一切片里的各条SFC的VNF序列长度均相同，分别为9, 10和11。仿真中利用函数随机生成DU池和CU池的基础设施网络，其设备数分别为12和18。任意设备上的计算资源和任意链路上的带宽资源均随机取值，计算能力取值范围分别为$\left[ {4,\;10} \right]$, [10¹¹, 10¹²] CPU周期/s，链路带宽取值$[100,$$200] \,{\rm{Mbps}}$, NGFI带宽为$1000\,{\rm{Mbps}}$。A-C学习过程设置200个学习回合，每个回合中步数为200。

为了讨论方便，先将系统中SFC总数量设置为50。首先，采用不同的学习率会影响A-C学习的收敛性能。如图3、图4所示，图3固定评论家学习率${\varepsilon _{c,t}} = 0.10$，改变演员学习率，图4固定演员学习率${\varepsilon _{a,t}} = 0.001$，改变评论家学习率。从上述两图可以看出，学习率设置过小，会使得收敛过程缓慢，在学习回合结束时曲线依旧呈下降趋势；而增大学习率，虽然能够加快收敛，但容易产生震荡，从而难以找到最佳收敛值。因此，选择${\varepsilon _{a,t}} = 0.001$, ${\varepsilon _{c,t}} = 0.10$作为后续仿真中的参数。

图  3  不同演员学习率A-C算法的收敛性

下载: 全尺寸图片 幻灯片

图  4  不同评论家学习率A-C算法的收敛性

下载: 全尺寸图片 幻灯片

采用不同优化器也会对A-C算法的收敛性能产生一定的影响。本文采用最常用的3种优化器进行比较，分别是随机梯度下降优化器(Stochastic Gradient Descent optimizer, SGD)、动量优化器(Momemtum optimizer)以及Adam优化器。如图5所示，在前100个回合中，Adam曲线的收敛速度优于另外两个优化器，但就最终收敛效果而言，Adam的系统时延收敛值更低且震荡幅度更小。这是因为SGD和Momentum在参数向量更新过程中都是固定学习率，而Adam却能够动态调整各个参数的学习率。

图  5  基于不同优化器的A-C算法的收敛性

下载: 全尺寸图片 幻灯片

接下来，将从队列稳定性方面评估该算法。如图6，随着学习过程的进行，尽管系统中的切片数据包到达率持续变化，但切片的队列积压情况会逐渐改善并最终收敛到一个较小的范围。这说明本文算法能够很好地实现与环境的交互，在每个学习回合中根据不断变化的数据包到达率逐步动态调整SFC的部署策略，稳定并减小队列积压。

图  6  3种切片的数据包到达率与队列积压和变化对照图

下载: 全尺寸图片 幻灯片

图7所示为VNF放置方式的选择频率与切片服务数据规模的关系。仿真参数中已设置切片3服务数据规模最大，其次是切片2，切片1最小。由图7可知，切片3选择方式3的频率最高，其次是方式4。这是因为这两种VNF放置方式对前传网络的传输时延要求较为宽松，能够减小切片对NGFI的带宽资源消耗。切片2的数据服务规模适中，选择方式5的频率较高，说明其可以适当选择时延较为严格的VNF放置方式。切片1对NGFI带宽资源的依赖性最小，因此选择方式7的频率最高。

图  7  3个切片的VNF放置方式选择统计图

下载: 全尺寸图片 幻灯片

为了更好地体现本文算法的性能，对比了文献[7]中的两种蚁群算法(Genetic Algorithm, GA)，文献[6]的卫星网络SFC部署算法(SFC Deployment in Satelite Network, SDSN)，以及仅基于策略梯度的强化学习算法(Policy-Based Algorithm, PBA)。如图8、图9所示，本文所提基于A-C学习的SFC部署算法的系统收敛时延效果和资源利用率都明显优于其他几种方案。其中，GA方案容易陷入局部最优解，SDSN方案忽略了资源的分配与各类时延之间的关联性，PBA方案在评价策略时不如A-C算法高效且方差较大。而本文所提基于A-C学习的SFC部署算法，结合了基于值函数和基于策略梯度两种方法，使得学习过程更加高效，并且将各类时延与资源分配建立关联，使得资源的分配更为合理。

图  8  不同算法的系统收敛时延

下载: 全尺寸图片 幻灯片

图  9  不同算法的资源利用率

下载: 全尺寸图片 幻灯片

最后，保持系统中的SFC总数量仍为50，但是3个切片的SFC数量比例改为4:4:2，且调换切片1和切片2的数据包到达率设置，切片3保持不变。如图10所示，TACA由于有相似任务的外来策略知识，因此在仿真中尤其是即刚开始的学习回合中，相比于传统A-C算法，其时延曲线波动明显更小，且迁移率因子越大，其收敛速度越快，最后学习回合结束时的收敛效果也更好。

图  10  不同迁移率因子的TACA算法收敛过程

下载: 全尺寸图片 幻灯片

6.   结束语

本文考虑在5G接入网DU/CU架构下，考虑实际网络中业务请求的随机性和未知性，针对SFC部署的系统端到端时延问题，提出了基于A-C学习的SFC部署方案。在该方案中，建立了以动态变化的队列长度和数据包到达率作为状态空间的MDP模型，并通过A-C学习算法求解，实现自适应动态调整SFC部署，优化系统总时延。同时，为了更进一步实现并提升该A-C学习算法在其他相似任务上的收敛性，引入迁移学习思想并提出了TACA算法。仿真结果表明，该种基于迁移A-C学习的SFC部署算法能够很好地与网络环境进行交互并适应环境的动态变化，提升整个网络的时延性能，更加高效地利用网络资源。