-
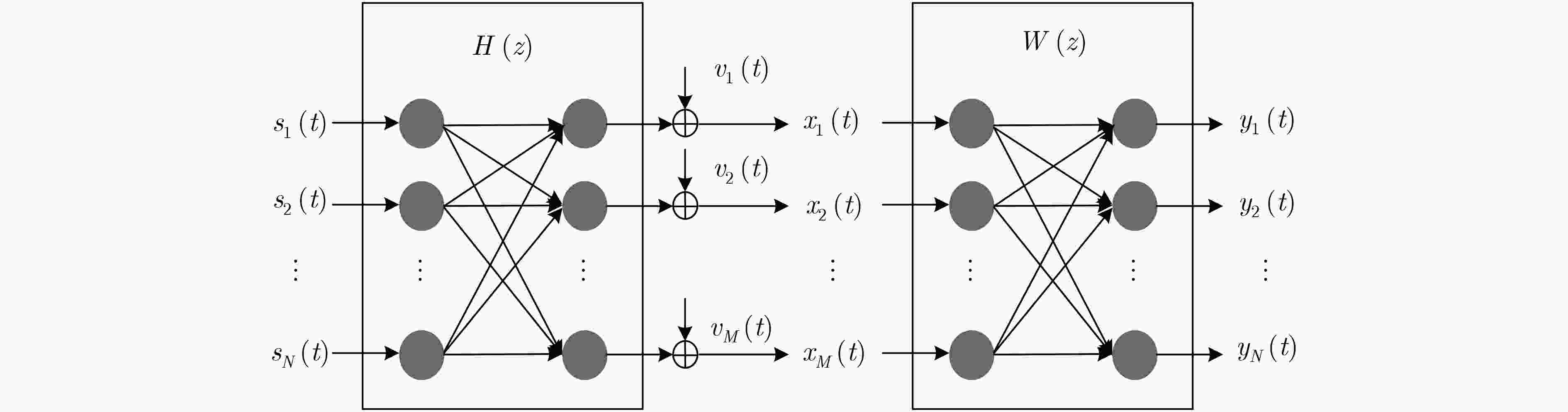
图 1 盲源分离模型结构图
Figure 1.
-
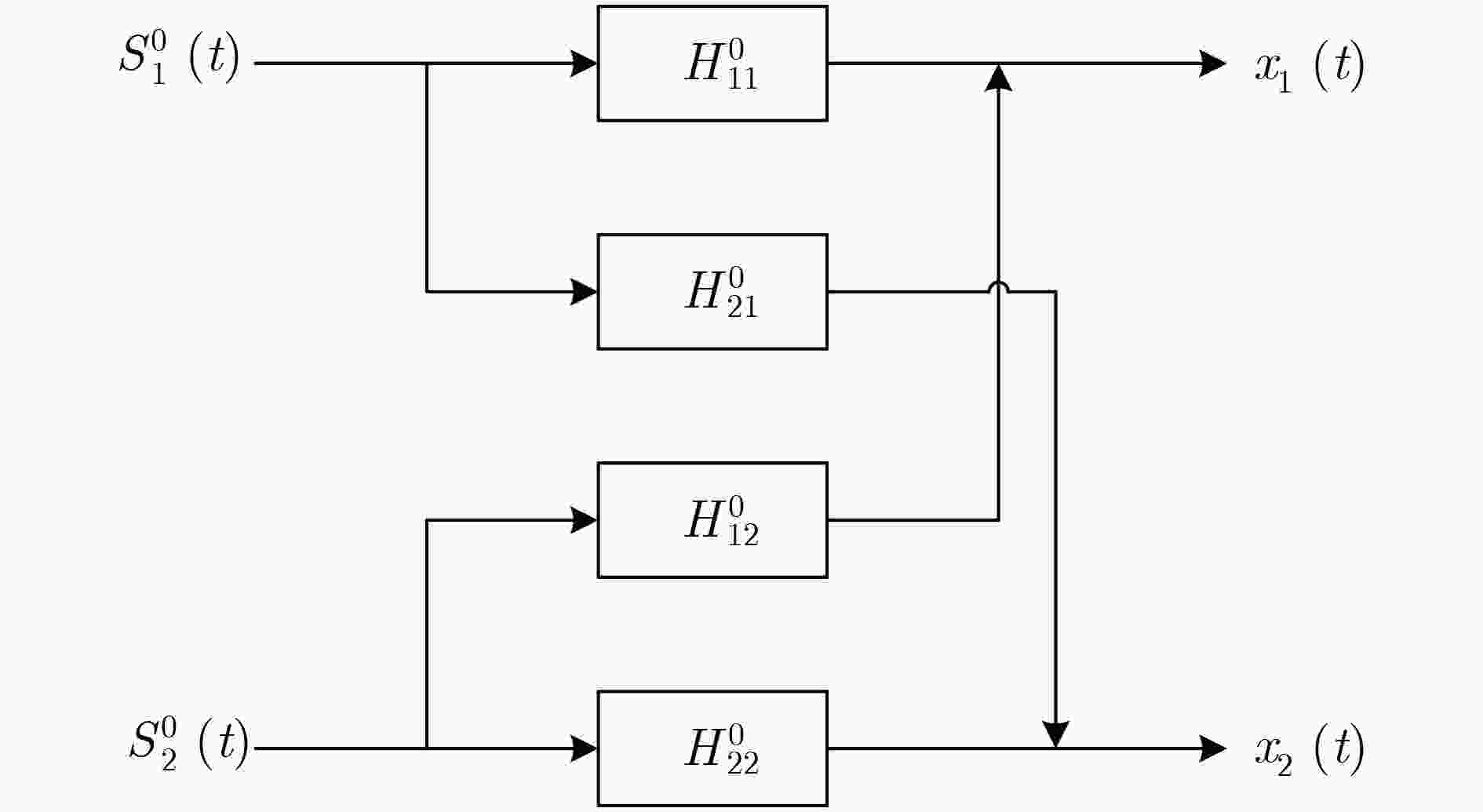
图 2 信号卷积混合滤波器模型
Figure 2.
-
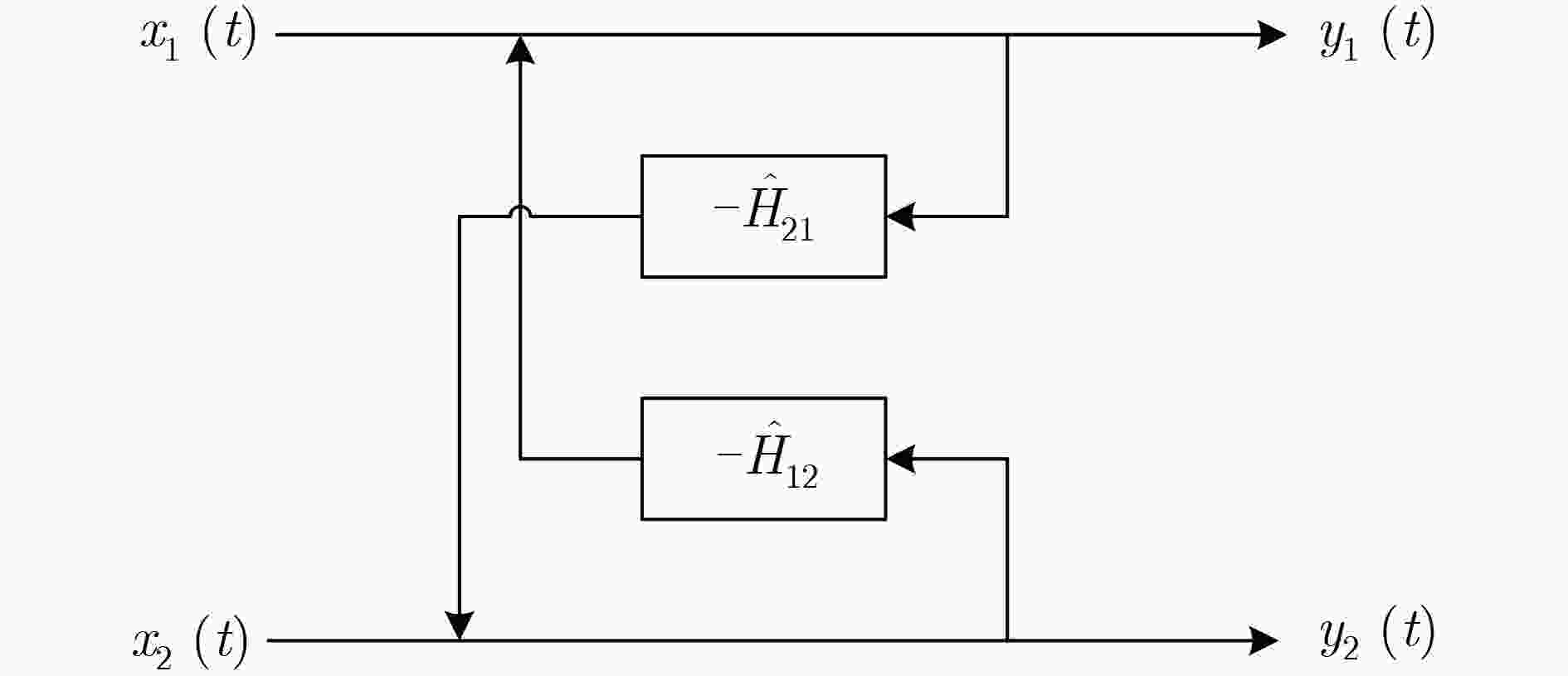
图 3 信号后向分离滤波器模型
Figure 3.
-
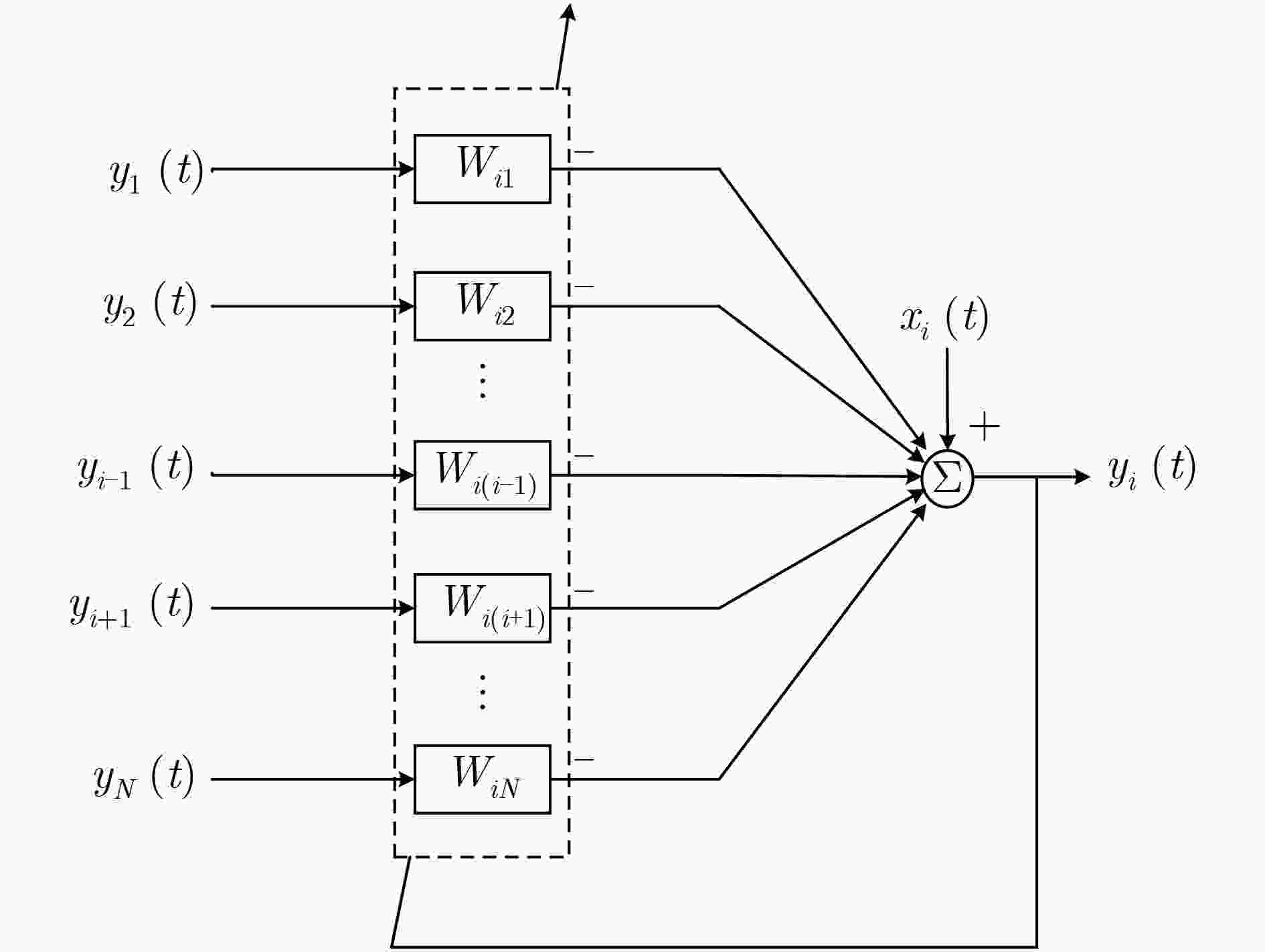
图 4 第i个通道的分离系统示意图
Figure 4.
-
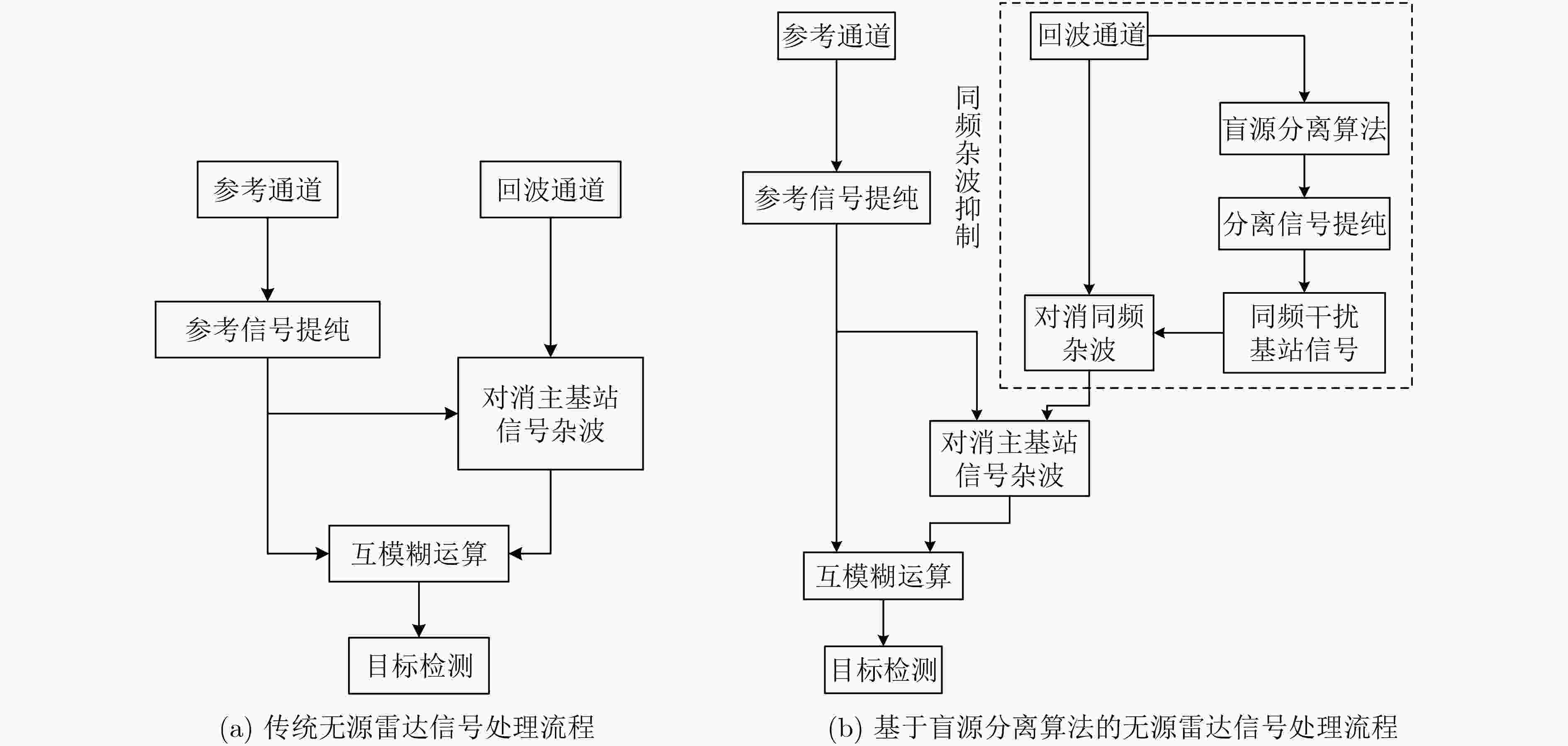
图 5 无源雷达信号处理流程图
Figure 5.
-
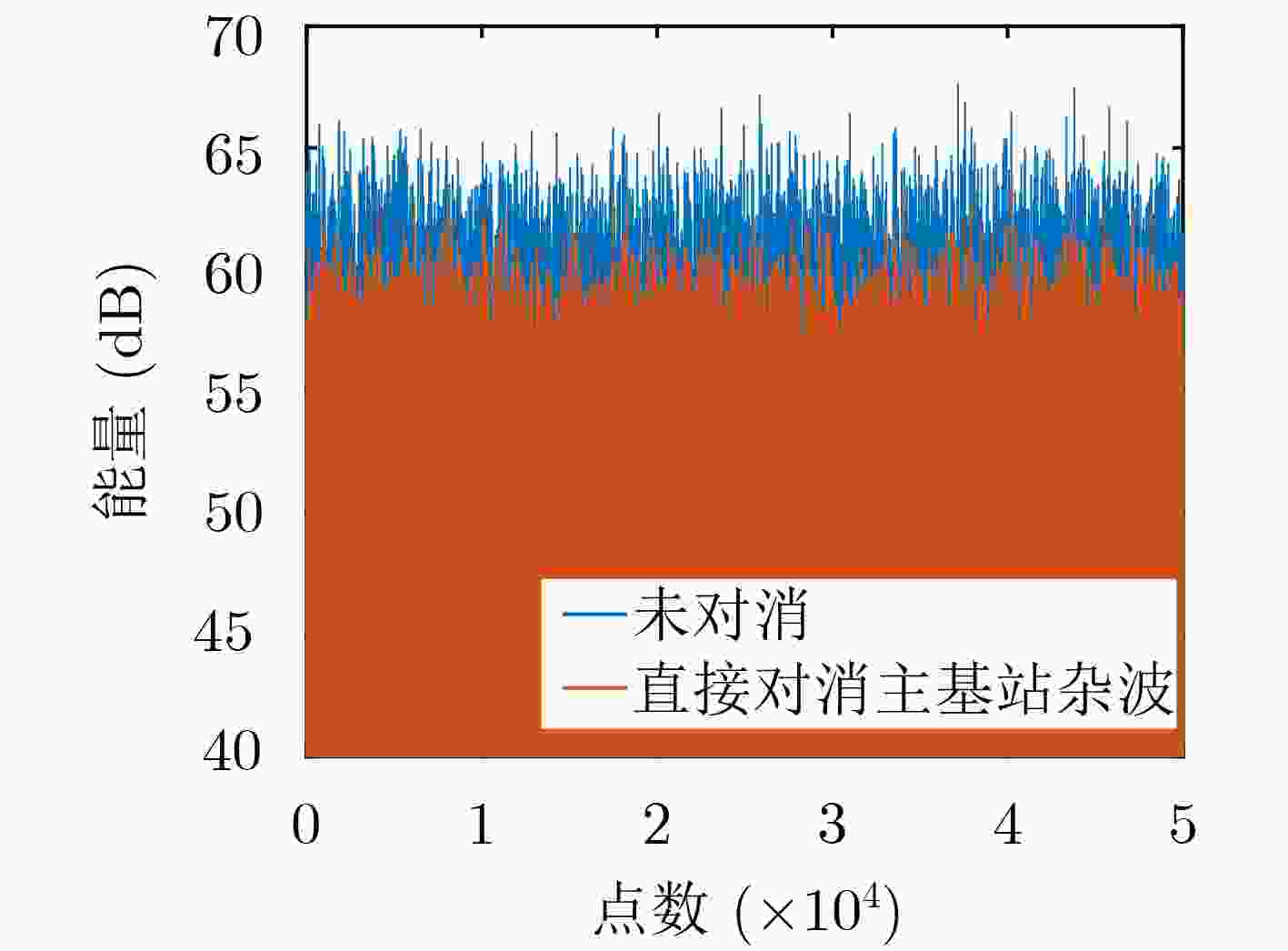
图 6 传统无源雷达杂波对消能量对比图
Figure 6.
-
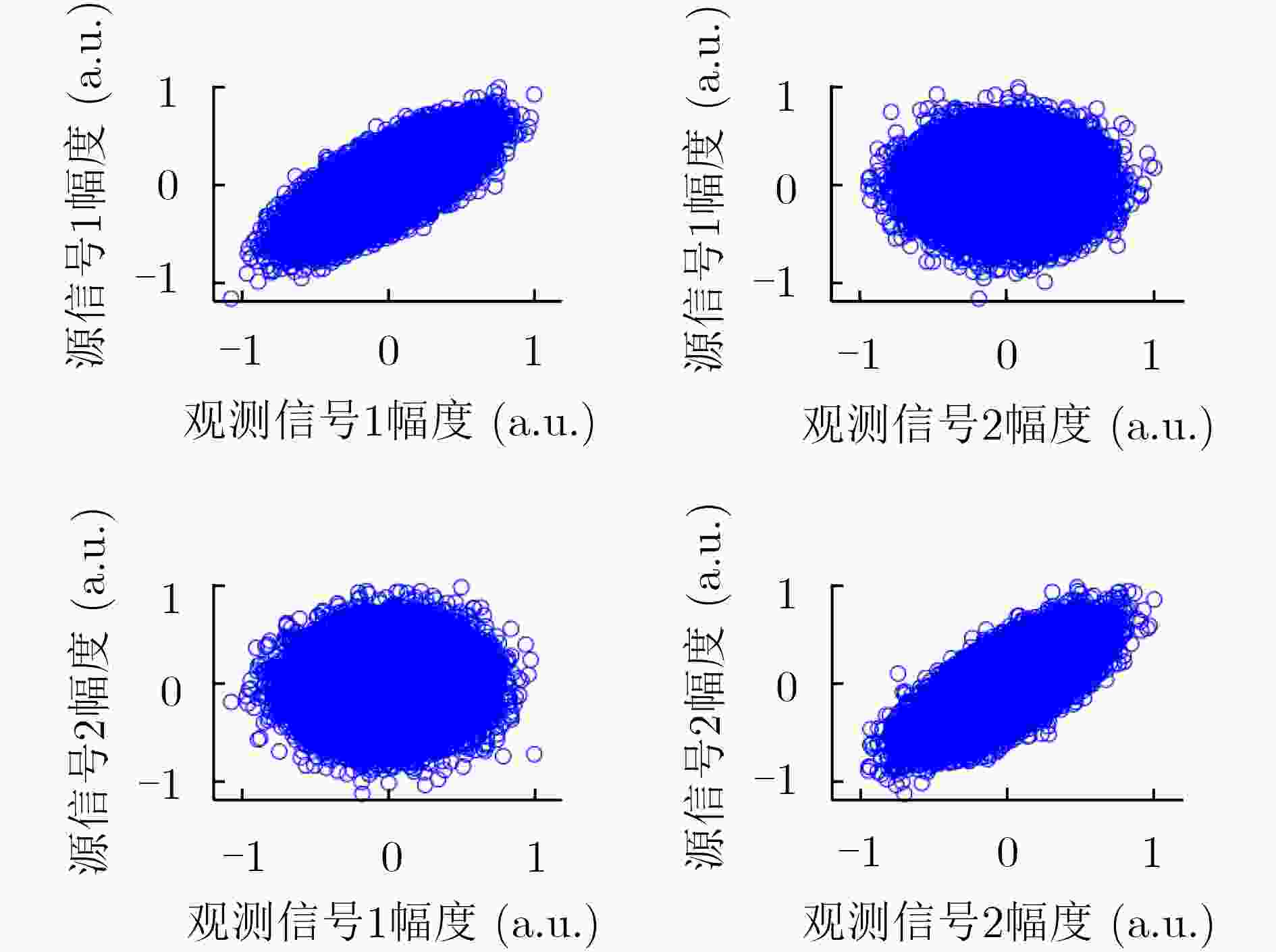
图 7 观测信号与源信号的散点图
Figure 7.
-
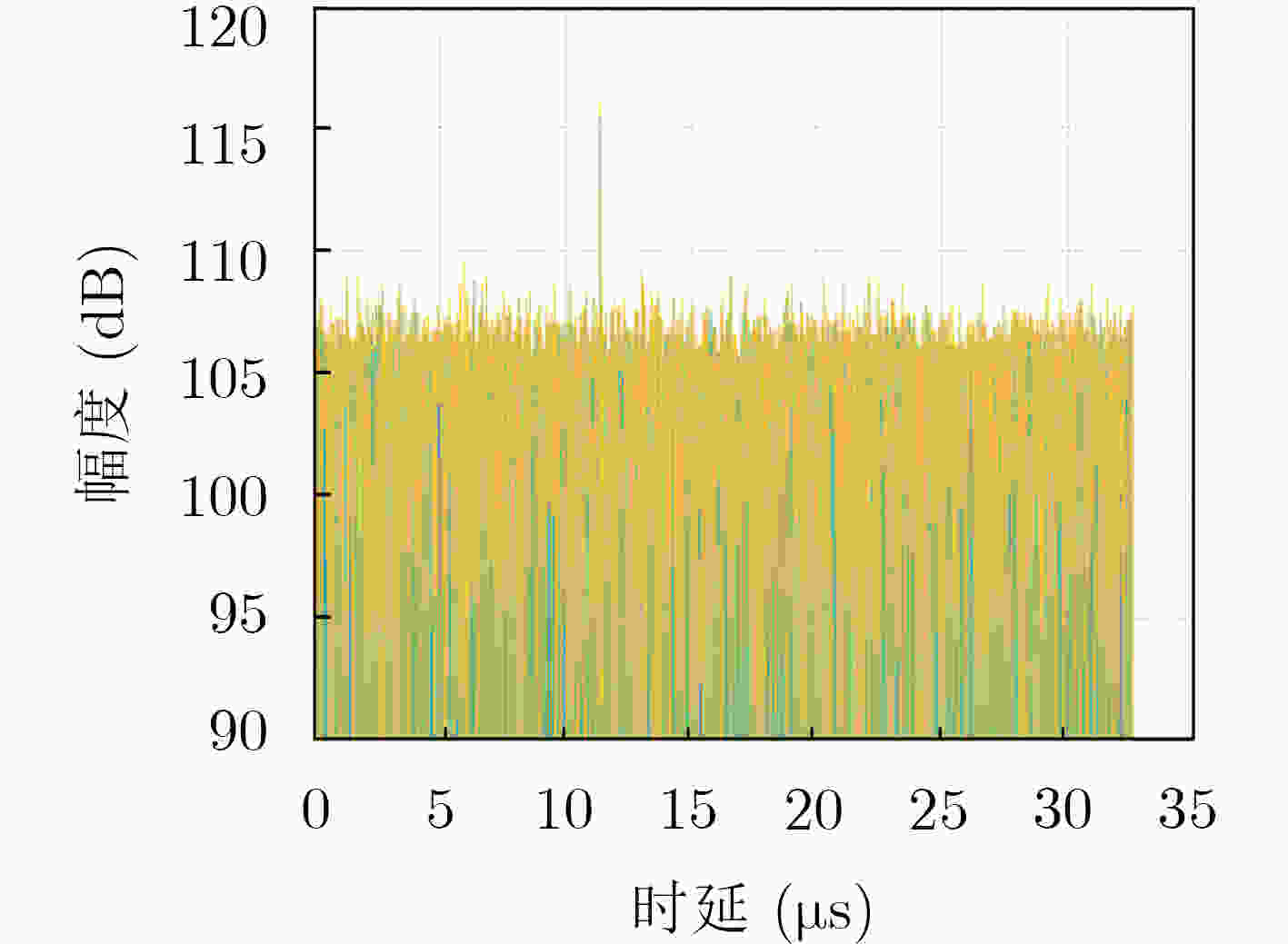
图 8 传统处理流程后的互模糊距离剖面图
Figure 8.
-
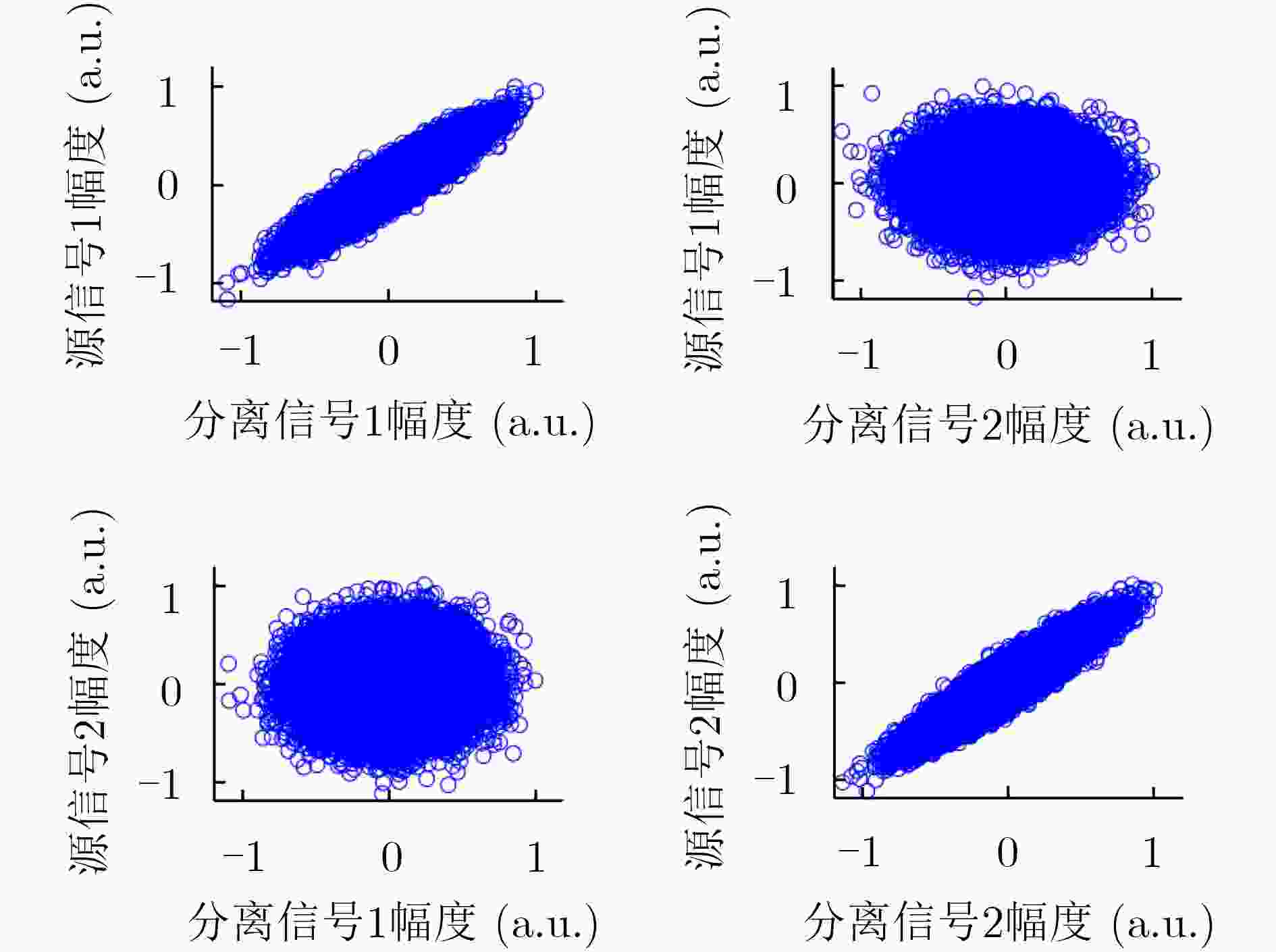
图 9 分离信号与源信号散点图
Figure 9.
-
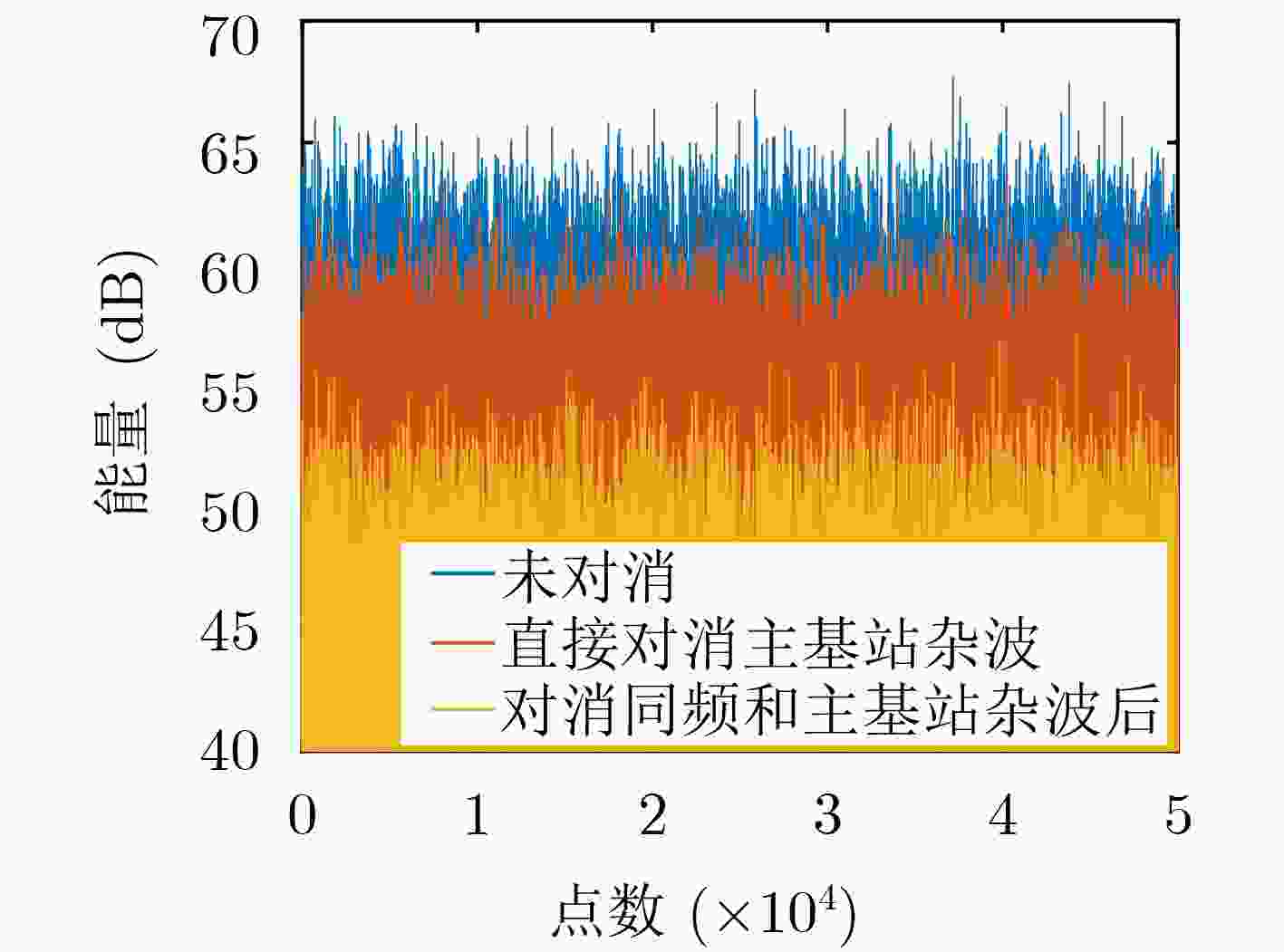
图 10 对消能量比较图
Figure 10.
-
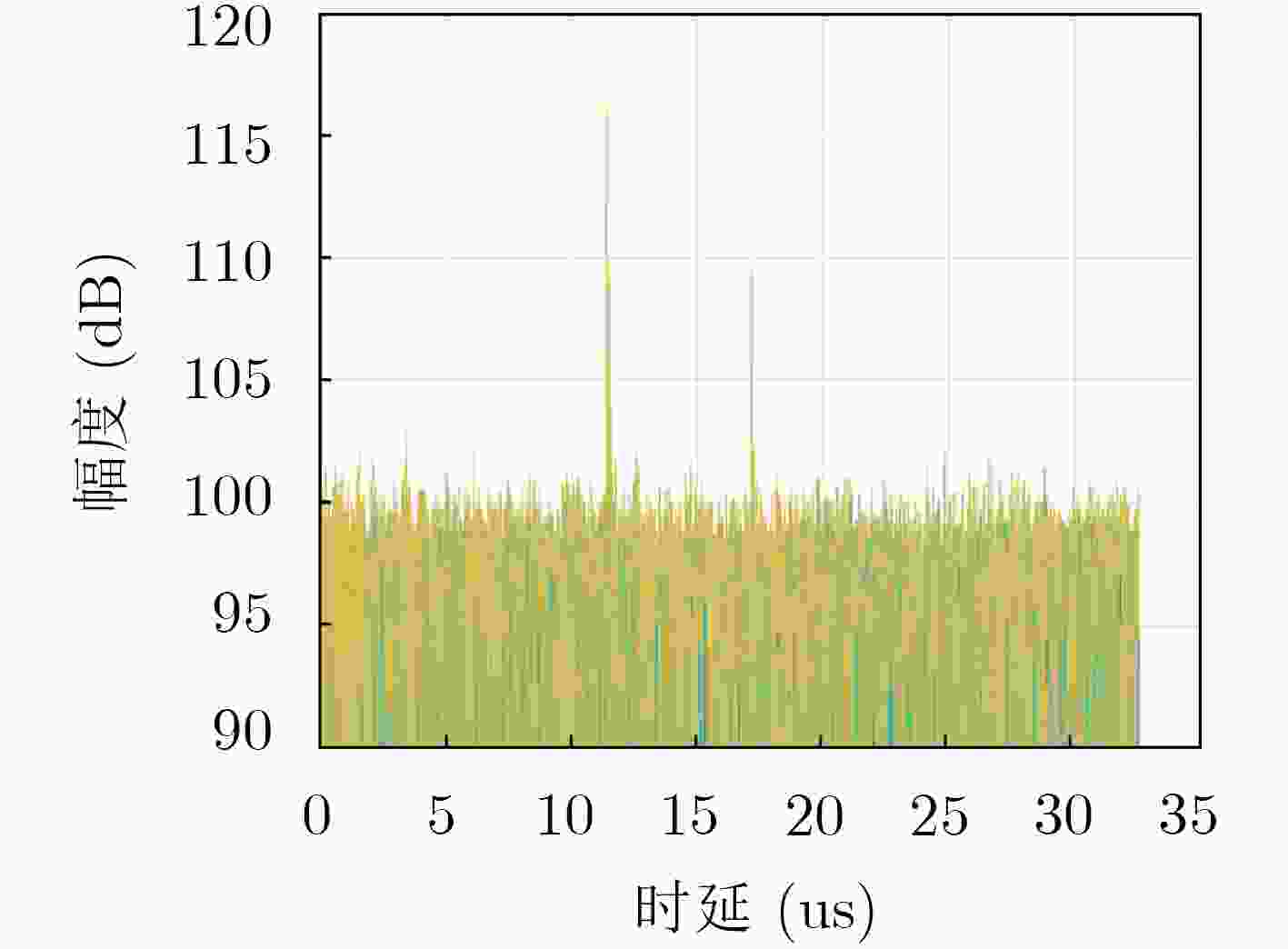
图 11 改进的处理流程后的互模糊距离剖面图
Figure 11.
-

图 12 噪声对杂波对消比的影响
Figure 12.
-
参数:$N$= 源数目,$M$= 观测信号数目
一般假设$N = M$
${K_i}$= 分离滤波器阶数,$i = 1,2, ··· ,N$
${\mu _{ij}}$= 步长,$i,j = 1,2, ··· ,N$,且$i \ne j$输入:${x_i}\left( t \right) = $观测信号,$i = 1,2, ··· ,N$ 初始化:${ {{W} }_{ {{ij} } } }\left( 0 \right) = { {{{\textit{0}}} }_{ {{Kj} } } }$, $i,j = 1,2, ··· ,N$,且$i \ne j$
${ {{Y} }_i}\left( t \right) = { {{{\textit{0}}} }_{Ki} }$, $i = 1,2, ··· ,N$
${K_i}$选取$K \ge \max \left\{ {{K_i},i = 1,2, ··· ,N} \right\}$
${\mu _{ij}}$根据输入数据进行调整计算:对$t = 1,2, ··· $,迭代计算:
${y_i}\left( t \right) = {x_i}\left( t \right) - \displaystyle\sum\nolimits_{j \ne i,j = 1}^N { {{W} }_{ij}^{\rm{T} }\left( {t - 1} \right){ {{Y} }_j}\left( t \right)} $
${{{W}}_{ij}}\left( t \right) = {{{W}}_{ij}}\left( {t - 1} \right) + {\mu _{ij}}{y_i}\left( t \right){{{Y}}_j}\left( t \right)$
${{{Y}}_i}\left( t \right) = {\left[ {{y_i}\left( {t - 1} \right),{y_i}\left( {t - 2} \right), ··· ,{y_i}\left( {t - {K_i}} \right)} \right]^{\rm{T}}}$
$i,j = 1,2, ··· ,N,i \ne j$终止条件:前后两次分离信号之间相关性系数的变化量小于所设
的误差门限输出:${y_i}\left( t \right) = $分离信号,$i = 1,2, ··· ,N$ 表 1 多通道LMS算法总结
-
主基站信号 同频干扰基站信号 时延(μs) 衰减(dB) 时延(μs) 衰减(dB) 直达波 0 0 0.07 –1 多径1 0.13 –8 0.20 –9 多径2 0.29 –11 0.36 –12 多径3 0.42 –15 0.59 –15 弱多径 0.16~1.95 –20~>–30 0.16~1.95 –20~>–30 目标1 11.39 –30 目标2 17.15 –37 表 2 回波通道1仿真参数
-
主基站信号 同频干扰基站信号 时延(μs) 衰减(dB) 时延(μs) 衰减(dB) 直达波 0.03 –2 0 –1 多径1 0.19 –8 0.16 –9 多径2 0.35 –14 0.36 –13 多径3 0.46 –19 0.49 –14 弱多径 0.16~1.95 –20~–30 0.16~1.95 –20~–30 表 3 回波通道2仿真参数
图共
12 个 表共
3 个