-
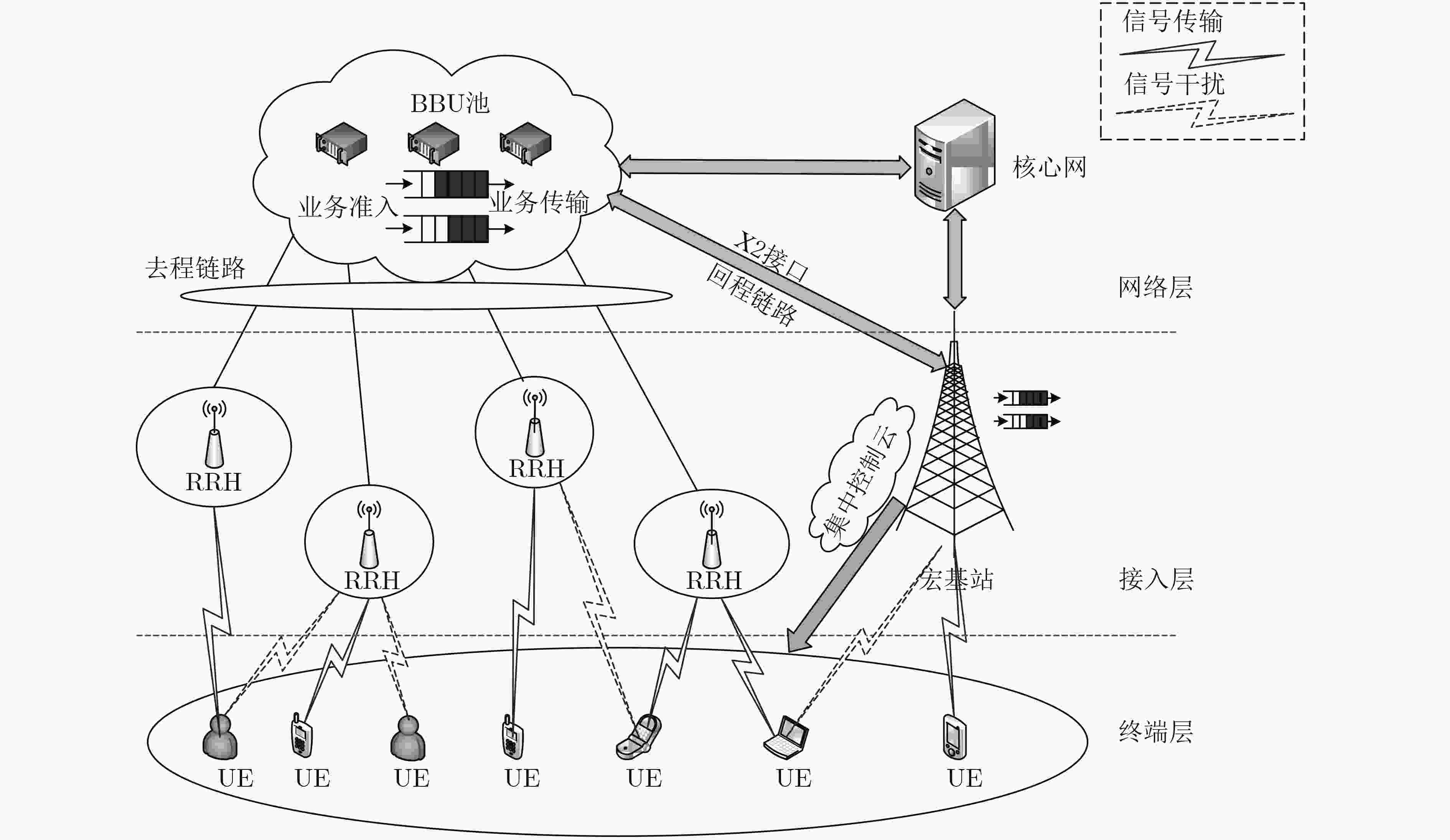
图 1 H-CRAN下行传输场景
Figure 1.
-
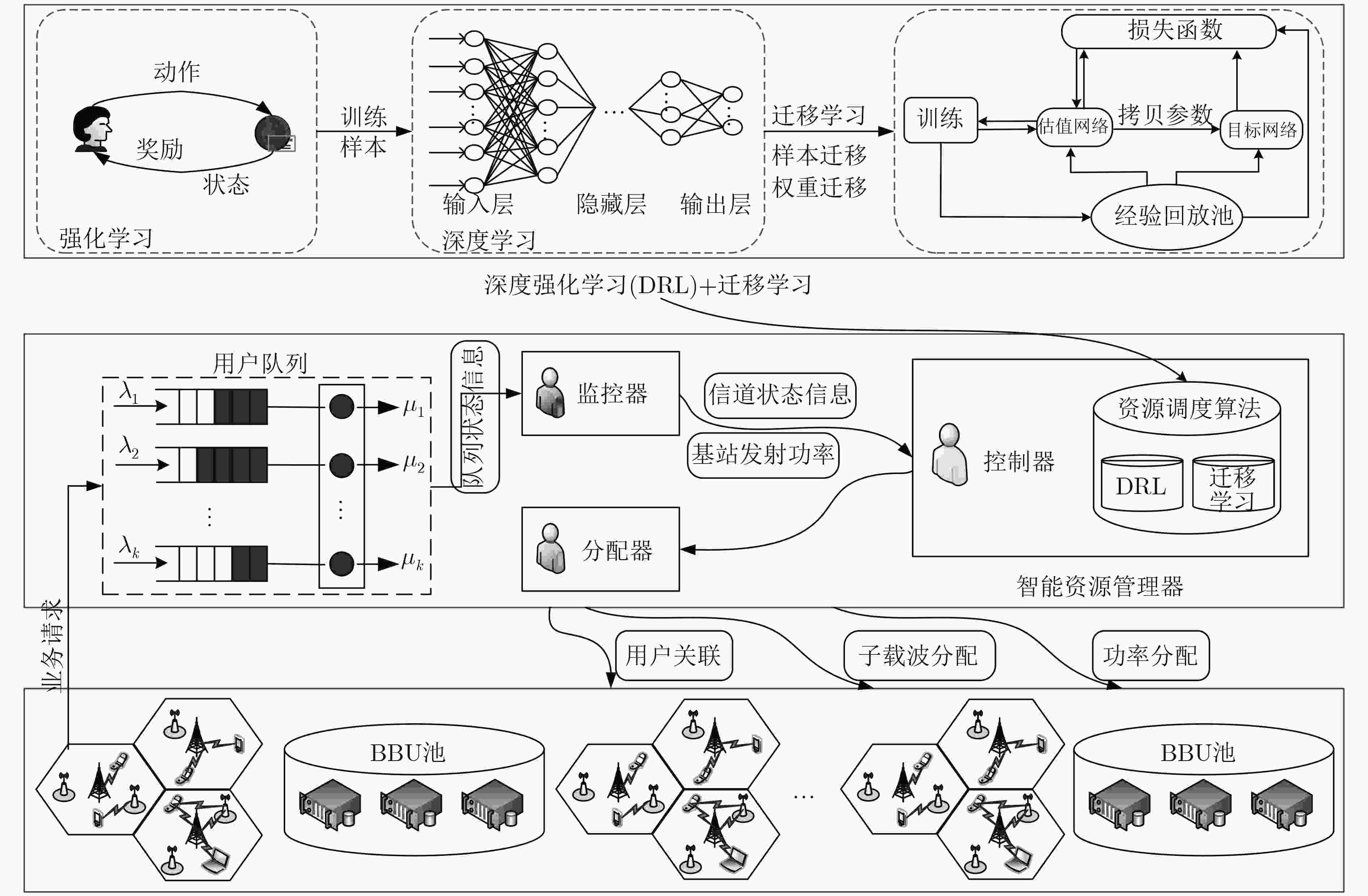
图 2 系统架构
Figure 2.
-
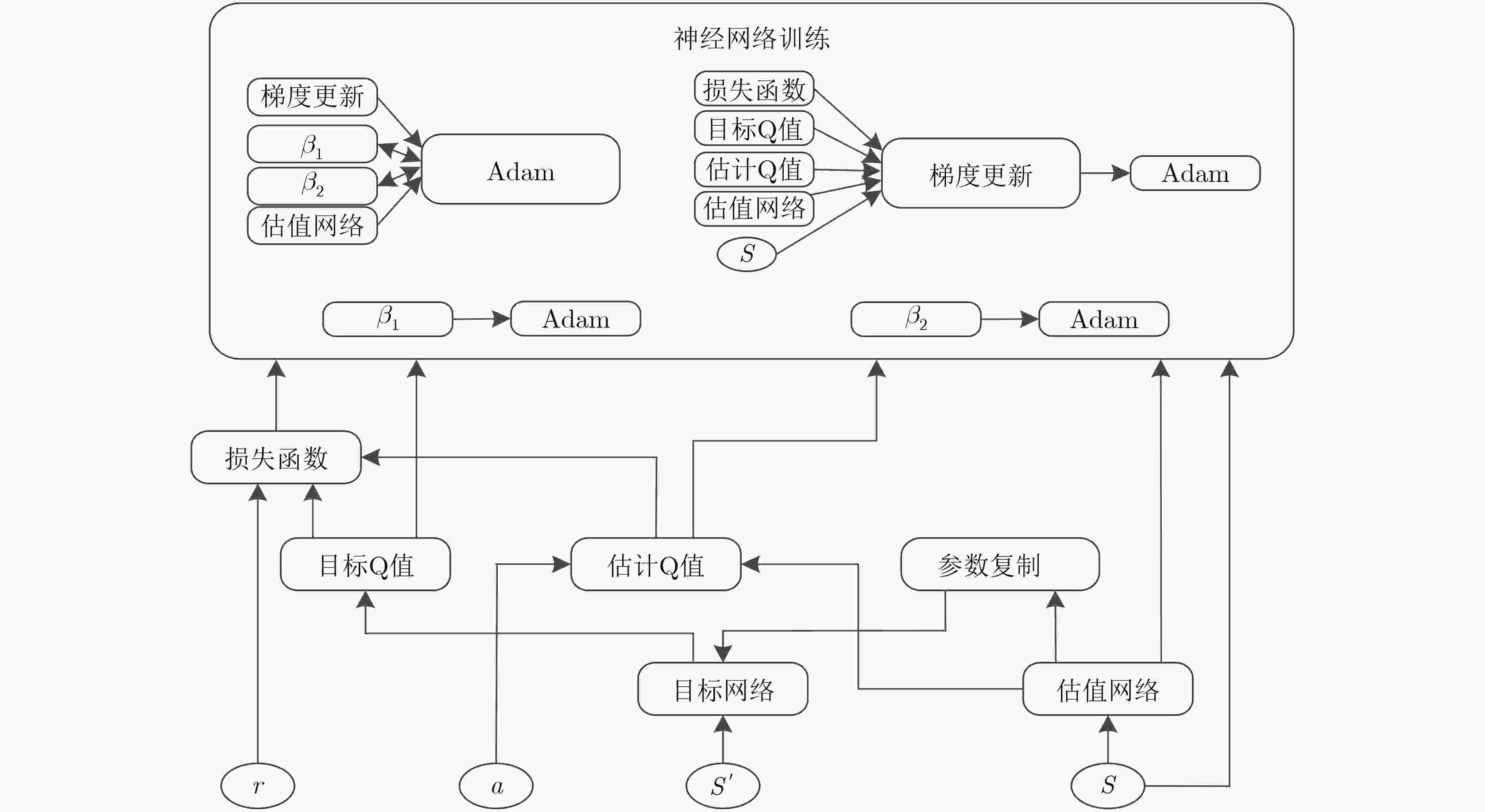
图 3 DQN算法框图
Figure 3.
-
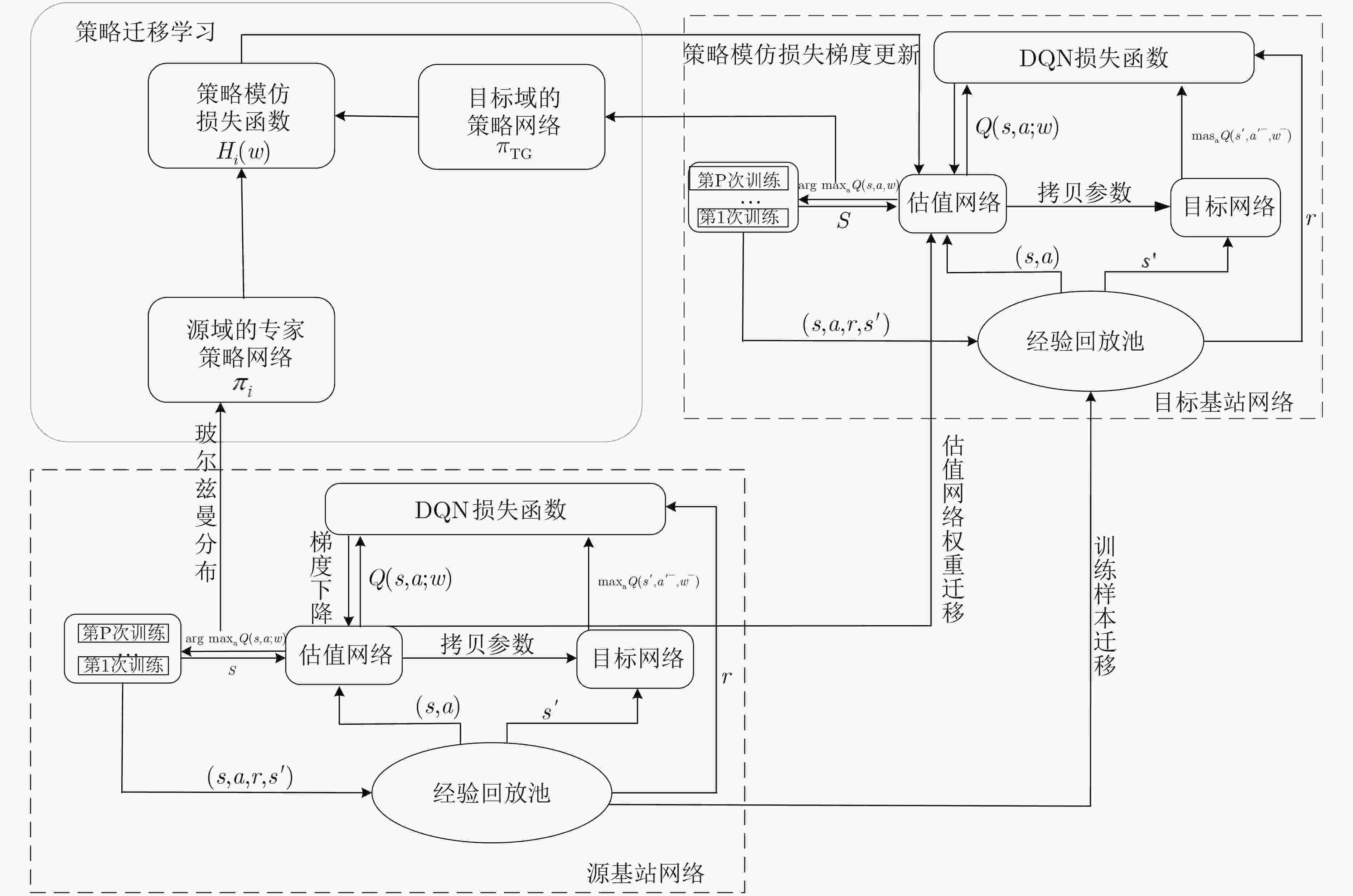
图 4 迁移学习场景图
Figure 4.
-
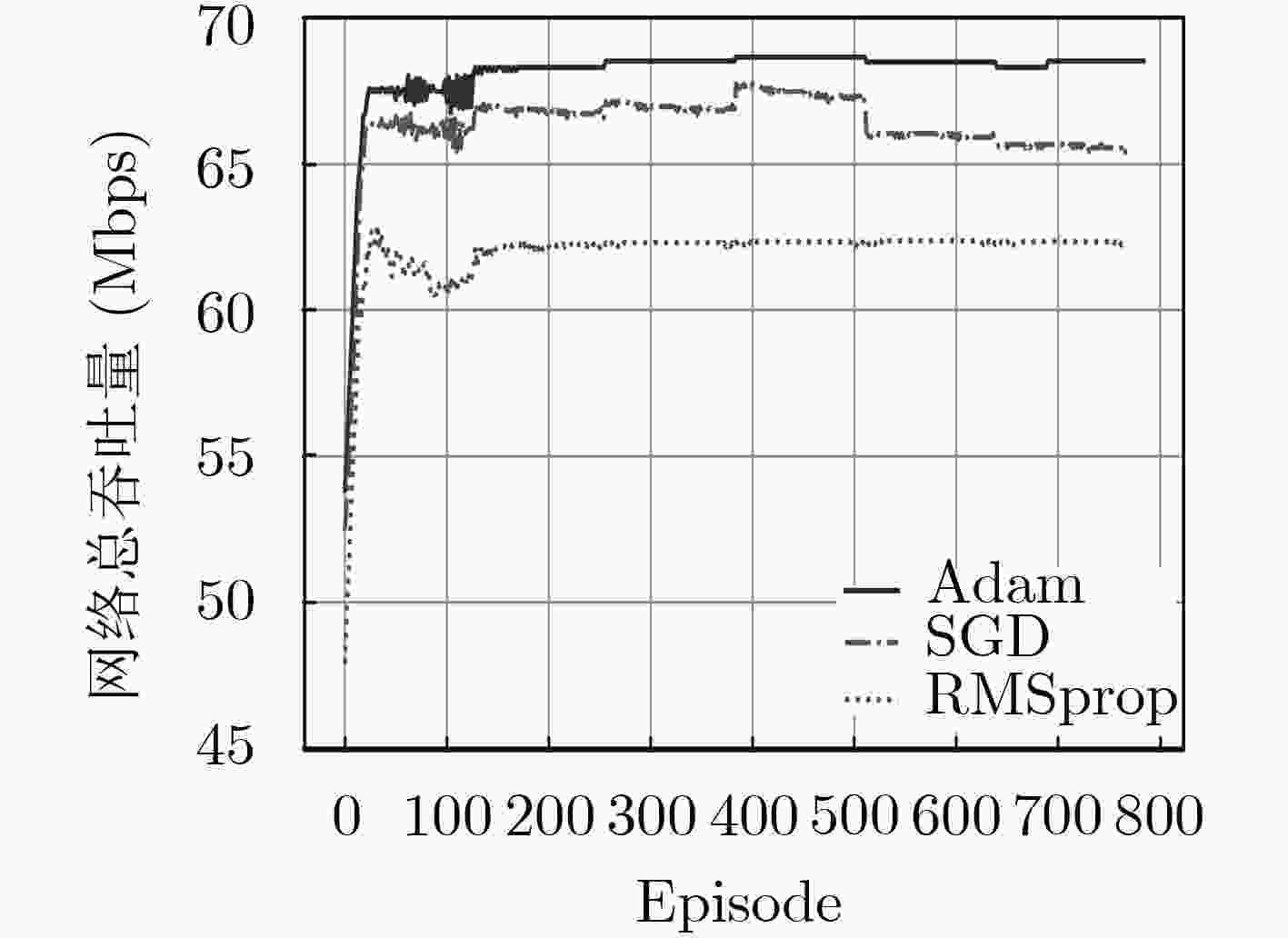
图 5 DQN中不同优化器下的网络总吞吐量
Figure 5.
-
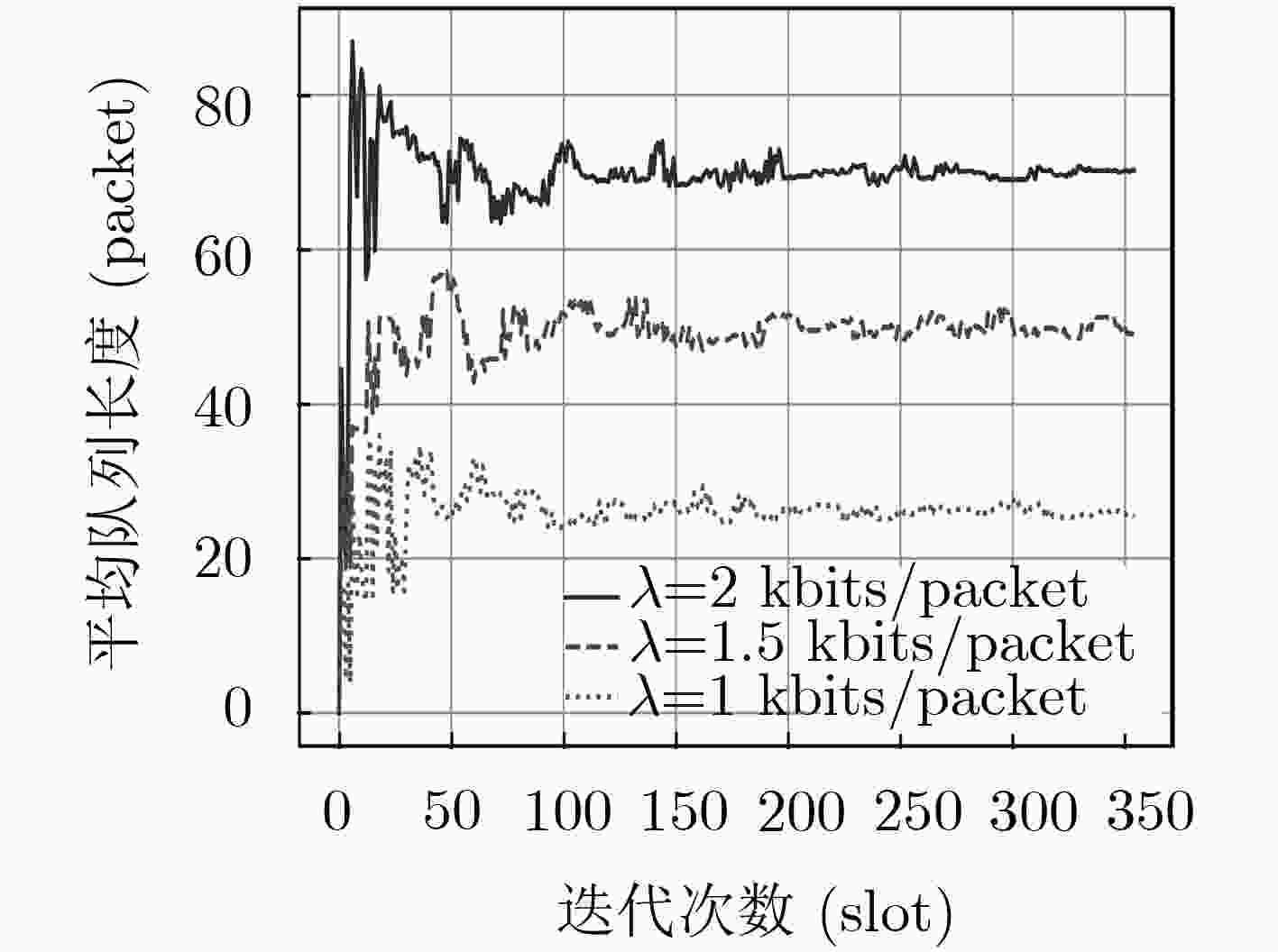
图 6 不同到达率下的平均队列长度
Figure 6.
-
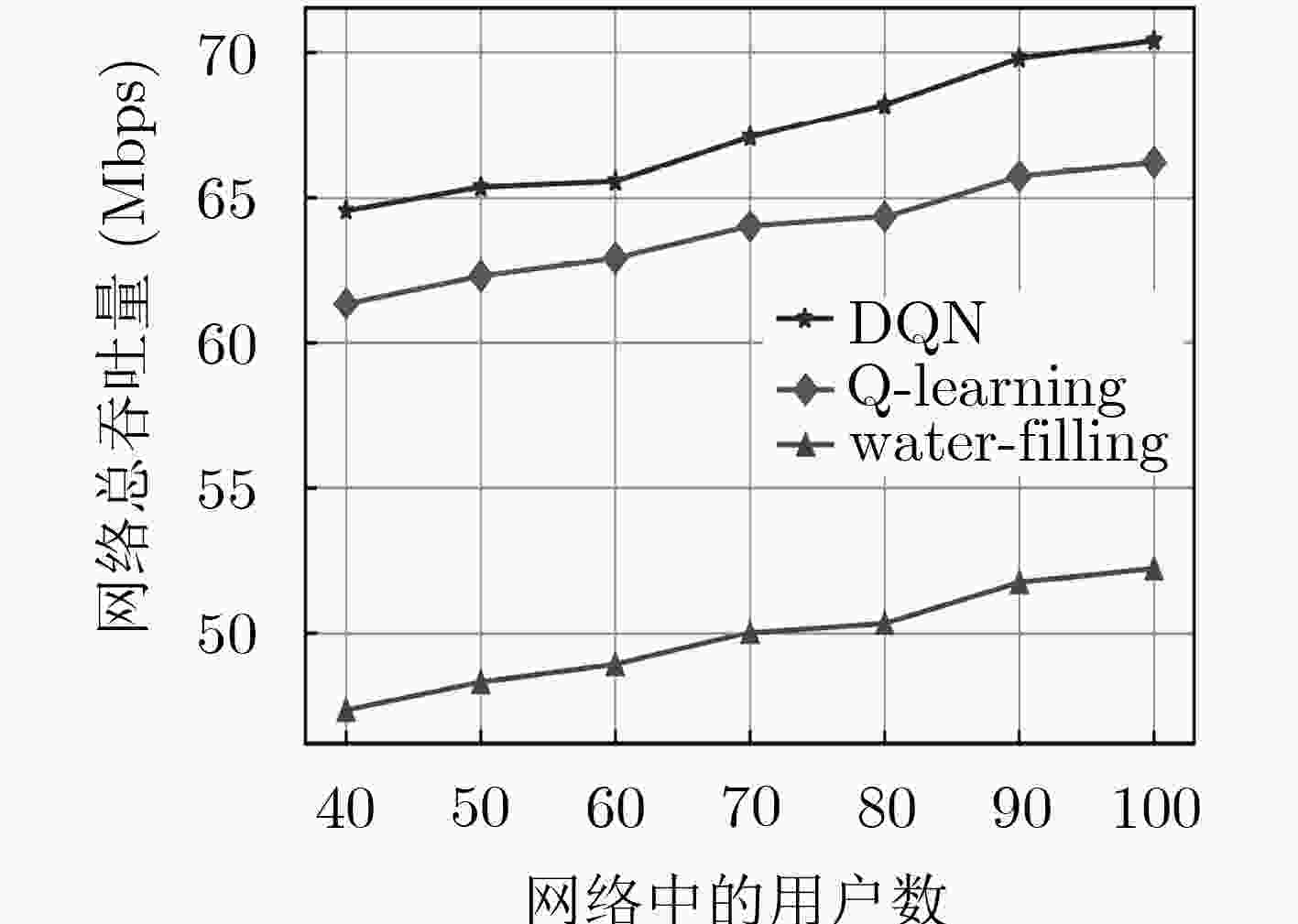
图 7 网络用户数的总吞吐量
Figure 7.
-
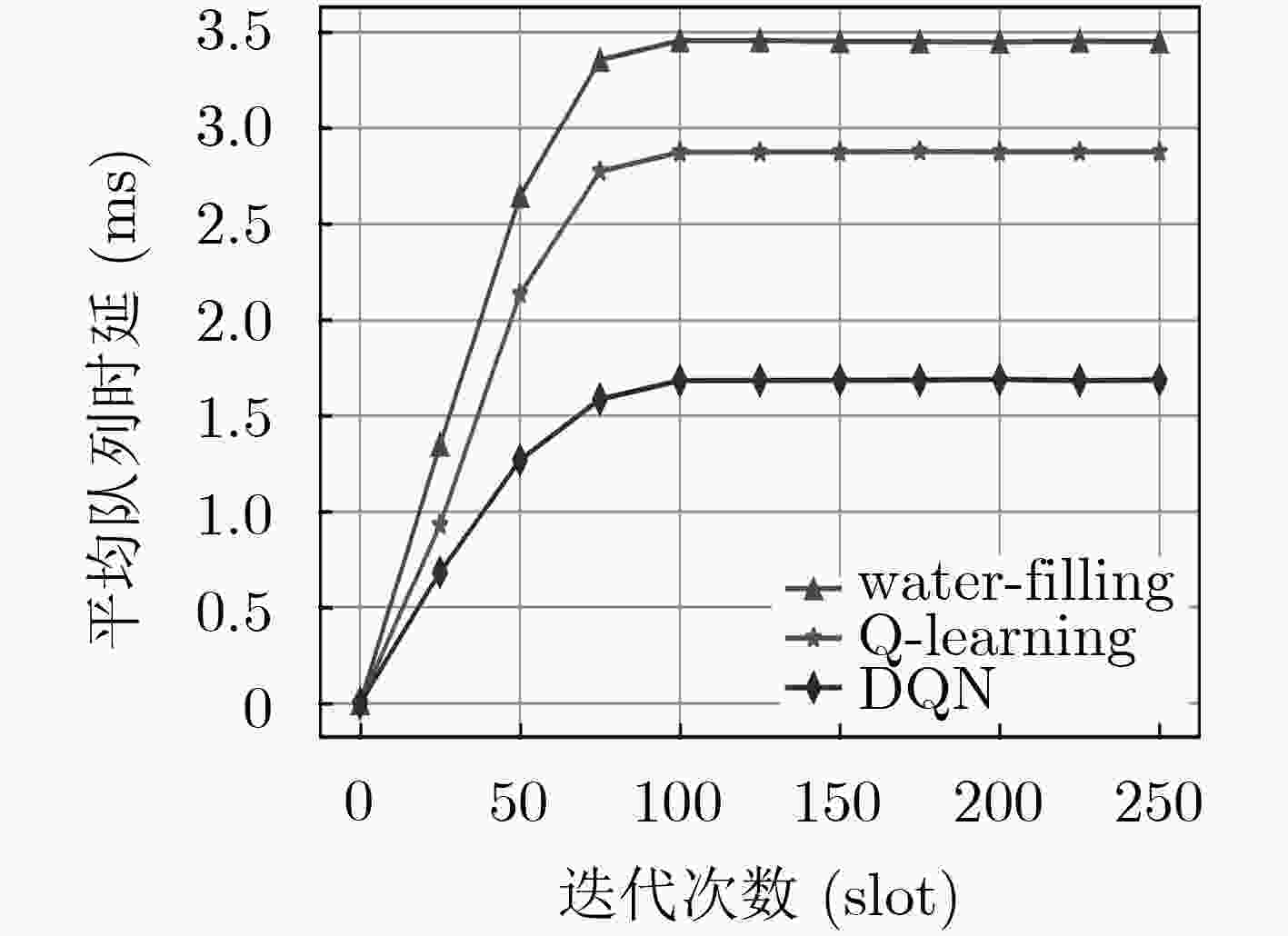
图 8 网络的平均队列时延
Figure 8.
-

图 9 迁移学习下的平均队列长度
Figure 9.
-
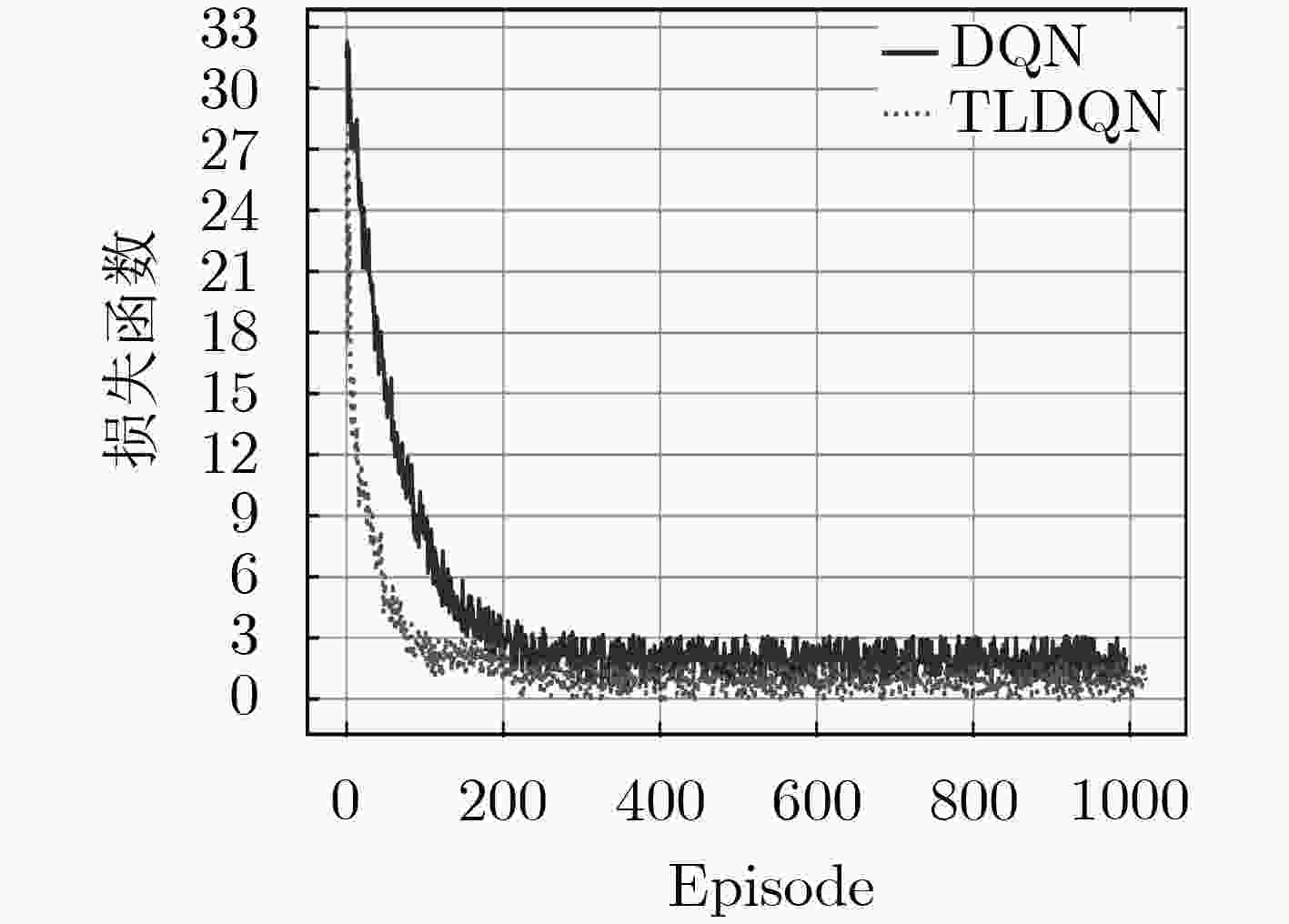
图 10 迁移学习下的损失函数
Figure 10.
-
算法1:DQN训练估值网络参数算法 (1) 初始化经验回放池 (2) 随机初始化估值网络中的参数$w$,初始化目标网络中的参数
${w^ - }$,权重为${w^ - } = w$(3) For episode $k = 0,1, ···,K - 1$ do (4) 随机初始化一个状态${s_0}$ (5) For $t = 0,1, ···, T - 1$ do (6) 随机选择一个概率$p$ (7) if $p \le \varepsilon $ 资源管理器随机选择一个动作$a(t)$ (8) else 资源管理器根据估值网络选取动作
${a^*}(t) = \arg {\max _a}Q(s,a;w)$(9) 执行动作$a(t)$,根据式(9)得到奖励值$r(t)$,并观察下一
个状态$s(t + 1)$(10) 将元组$(s(t),a(t),r(t),s(t + 1))$存储到经验回放池中 (11) 从经验回放池中随机抽取选取一组样本
$(s(t),a(t),r(t),s(t + 1))$(12) 通过估值网络和目标网络的输出损失函数,利用式(13),
(14)计算1, 2阶矩(13) Adam算法通过式(15),式(16)计算1阶矩和2阶矩的偏差
修正项(14) 通过神经网络的反向传播算法,利用式(17)来更新估值
网络的权重参数$w$(15) 每隔$\delta $将估值网络中的参数$w$复制给参数${w^ - }$ (16) End for (17) End for (18) 获得DQN网络的最优权重参数$w$ 表 1 算法1
-
算法2:基于TLDQN的策略知识迁移算法 (1) 初始化: (2) 源基站的DQN参数$w$,策略网络温度参数$T$,目标网络
的DQN参数$w'$(3) For 对于每个状态$s \in {{S}}$,源基站的动作$\overline a $,目标基站可能采
取的动作$a$ do(4) 执行算法1,得到估值网络的参数$w$,以及输出层对应的
$Q$值函数(5) 根据式(18)将源基站上的$Q$值函数转化为策略网络
${ {\pi} _i}(\overline a \left| s \right.)$(6) 根据式(19)将目标基站上的$Q$值函数转化为策略网络
${ {\pi} _{\rm{TG} } }(a\left| s \right.)$(7) 利用式(20)构建策略模仿损失的交叉熵$H(w)$ (8) 根据式(21)进行交叉熵的迭代更新,再进行策略模仿的偏
导数的计算。(9) 直至目标基站选取出的策略达到
${Q_{\rm{TG}}}(s,a) \to {Q^*}_{\rm{TG}}(s,a)$(10) End for (11) 目标基站获得对应的网络参数$w'$ (12) 执行算法1,目标基站得到最优资源分配策略 表 2 算法2
图共
10 个 表共
2 个