-
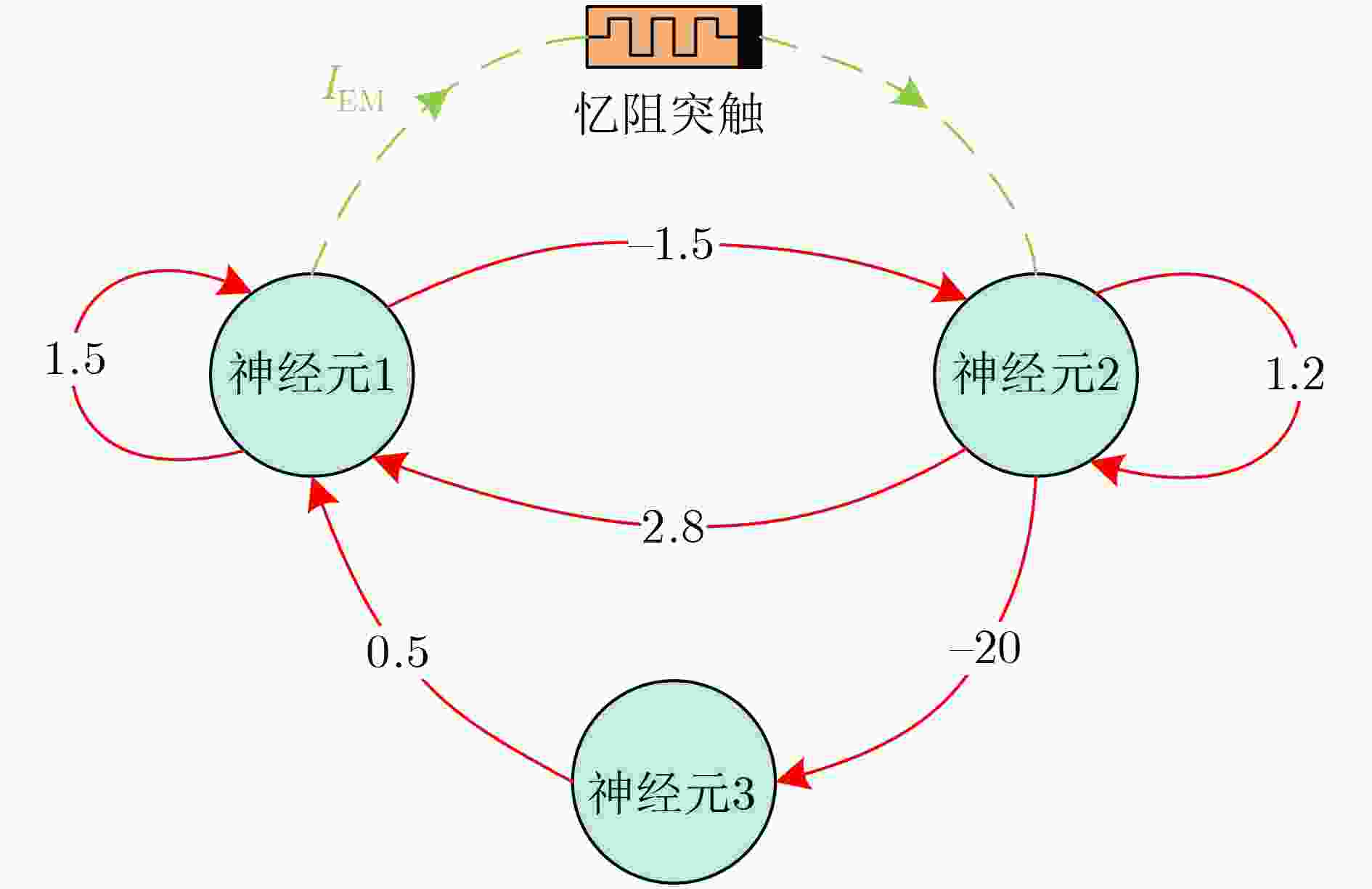
图 1 基于非理想忆阻突触的HNN的连接拓扑
Figure 1.
-
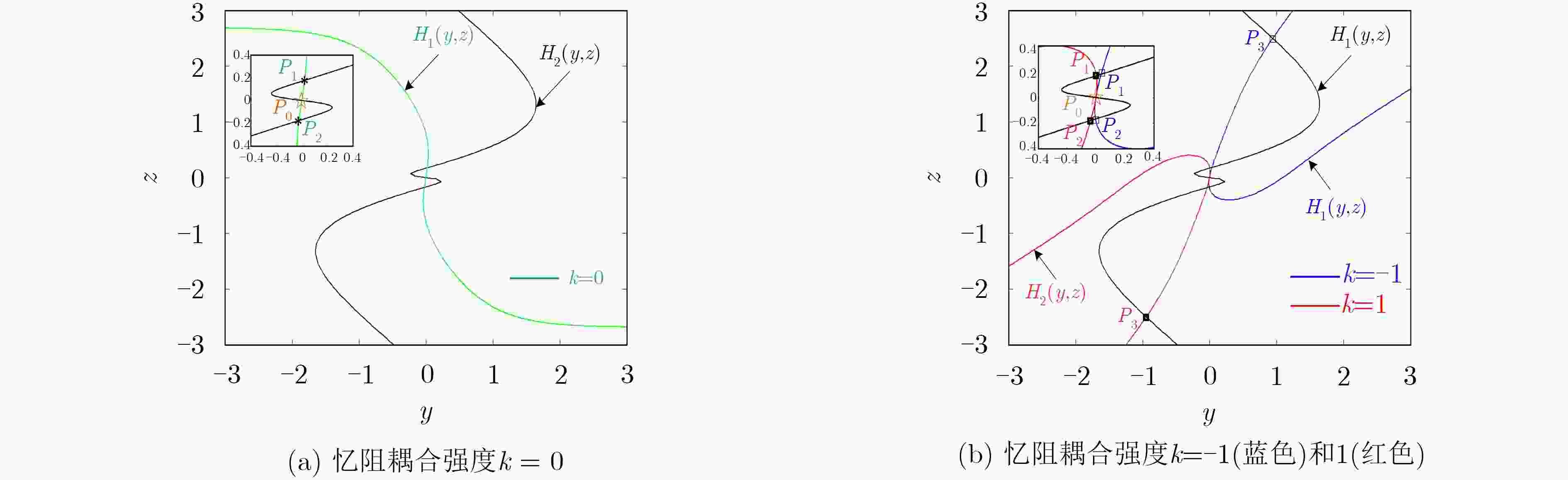
图 2 不同忆阻耦合强度时H1(y, z)和H2(y, z)函数曲线及交点平衡点
Figure 2.
-

图 3 不同初值下随参数k变化的共存分岔行为
Figure 3.
-

图 4 不同忆阻耦合强度下x1–x3平面上的相轨图
Figure 4.
-
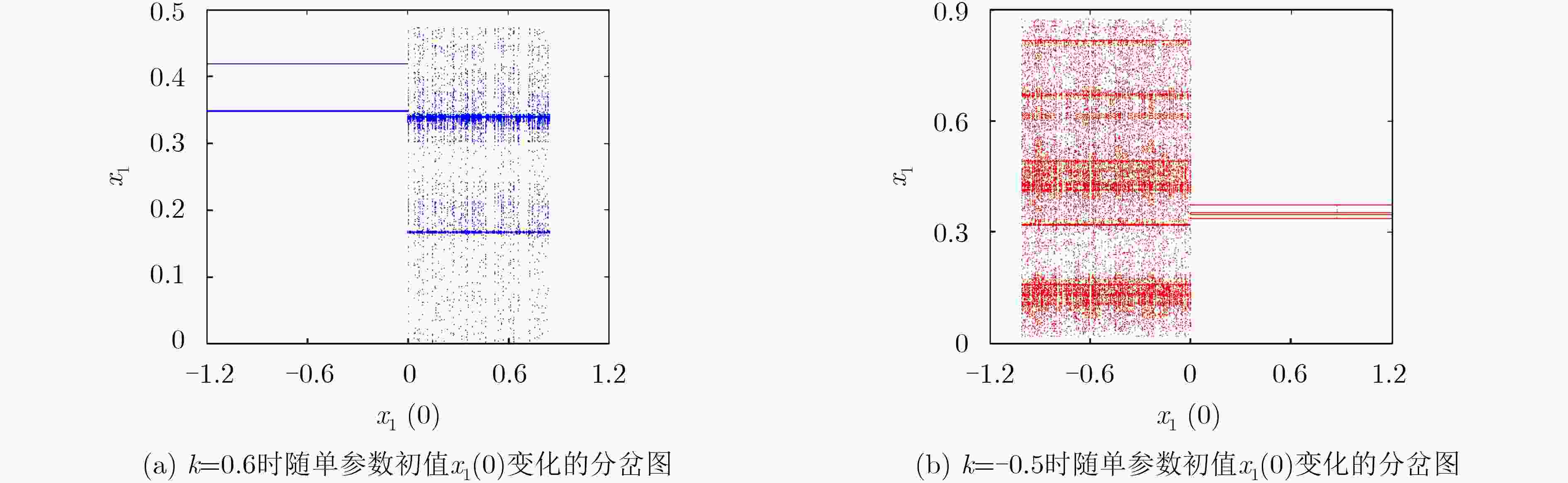
图 5 状态变量x1随状态初值变化的分岔图
Figure 5.
-
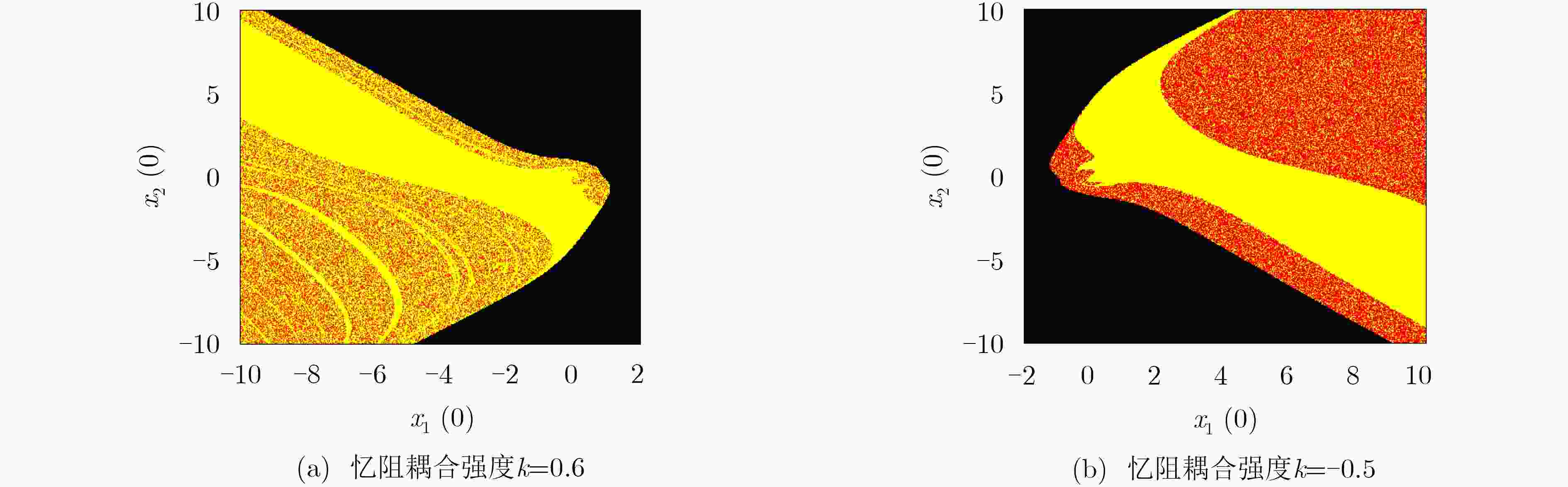
图 6 不同忆阻耦合强度下x1(0)–x2(0)平面的吸引盆
Figure 6.
-

图 7 不同忆阻耦合强度下共存吸引子在x1–x3平面的相轨图
Figure 7.
-
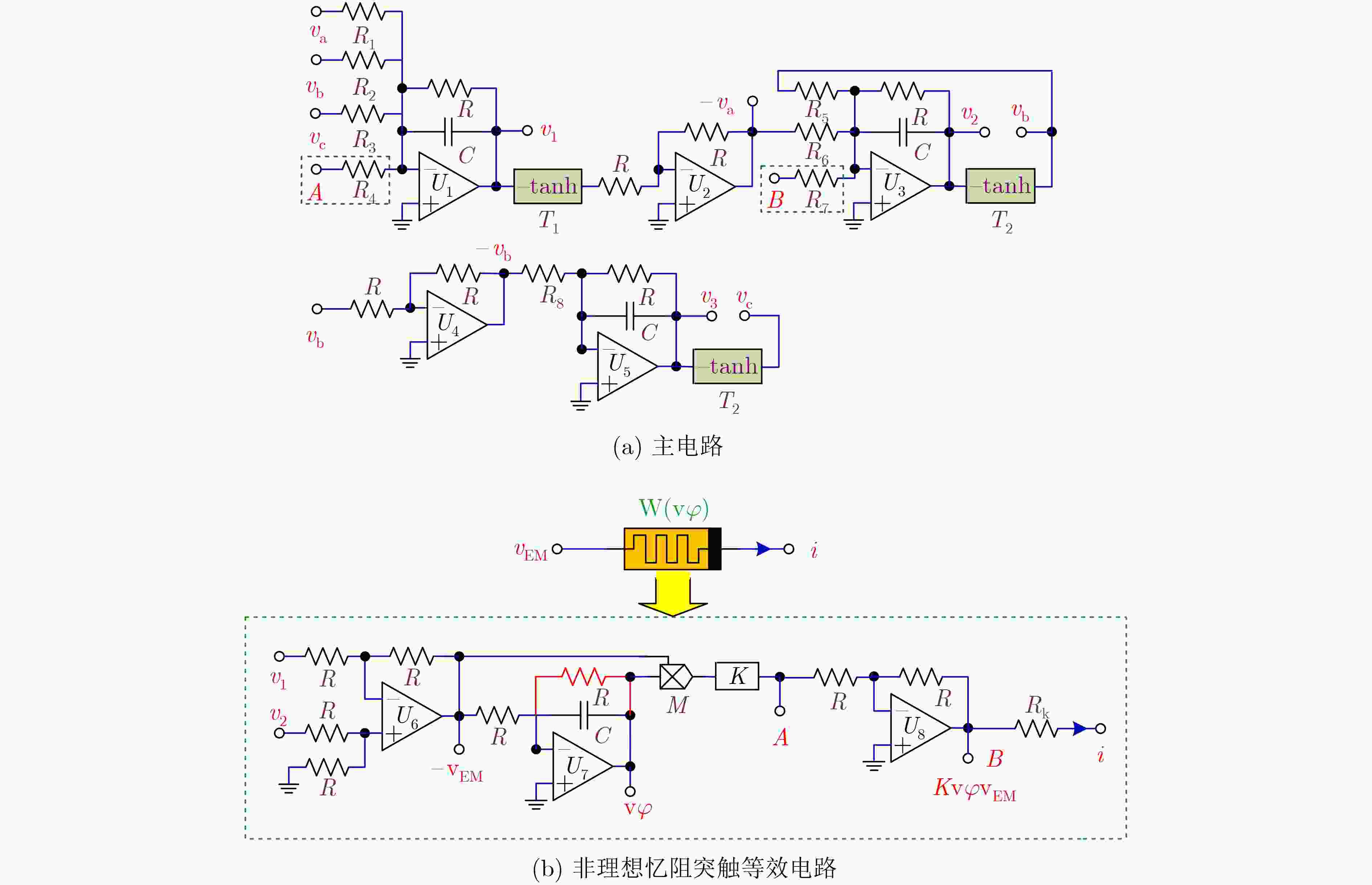
图 8 忆阻HNN模型(2)的等效实现电路
Figure 8.
-
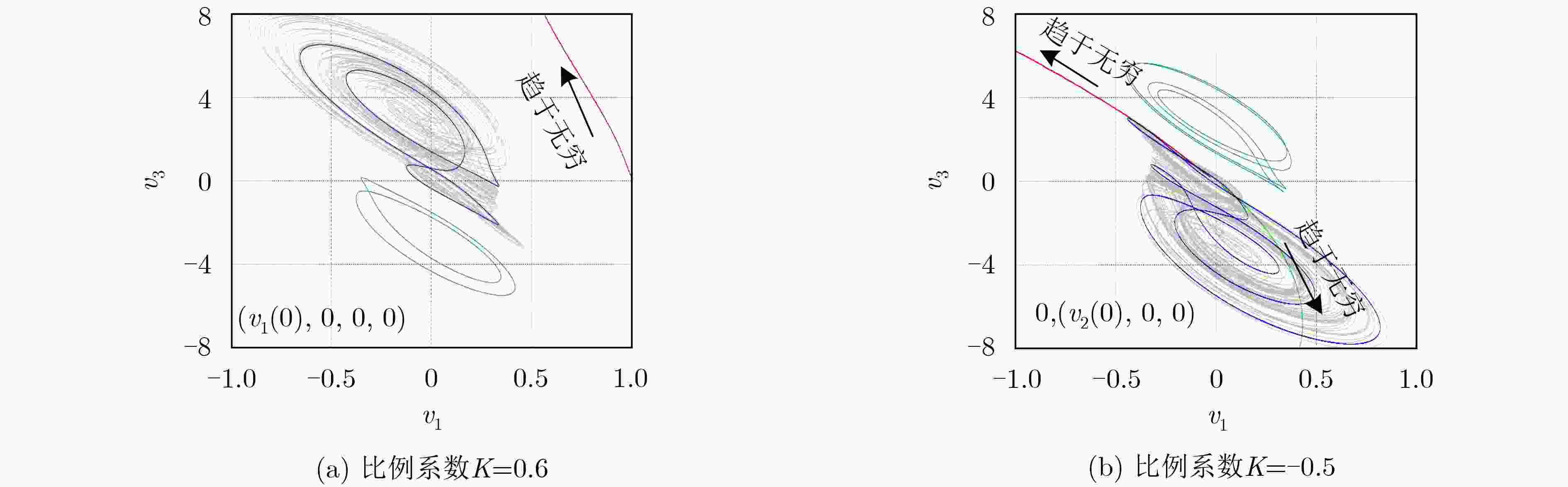
图 9 PSIM电路仿真得到的共存吸引子在v1–x3平面上的相轨图
Figure 9.
-
k 平衡点 特征值 稳定性 –1 P0: (0, 0, 0, 0) 1.6062, –0.9531±j2.3986, –1 不稳定指数1鞍焦 P1: (–0.0019, –0.1689, 3.3462, 0.1670) 0.0981±j2.0026, –0.8763, –0.9875 不稳定指数2鞍焦 P2: (0.0369, 0.1814, –3.5887, –0.1445) 0.5146±j2.0051, –0.9923, –1.0882 不稳定指数2鞍焦 P3: (0.9448, 2.5018, –19.7332, –1.5570) 3.4659, –0.9464, –1, –1.6894 不稳定鞍点 0 P0: (0, 0, 0, 0) 1.6062, –0.9531±j2.3986, –1 不稳定指数1鞍焦 P1: (0.0220, 0.1761, –3.4860, –0.1541) 0.3267±j2.0074, –0.9906, –1 不稳定指数2鞍焦 P2: (–0.0220, –0.1761, 3.4860, 0.1541) 0.3267±j2.0074, –0.9906, –1 不稳定指数2鞍焦 1 P0: (0, 0, 0, 0) 1.6062, –0.9531±j2.3986, –1 不稳定指数1鞍焦 P1: (–0.9448, –2.5018, 19.7332, 1.5570) 3.4659, –0.9464, –1, –1.6894 不稳定鞍点 P2: (–0.0369, –0.1814, 3.5887, 0.1445) 0.5146±j2.0051, –0.9923, –1.0882 不稳定指数2鞍焦 P3: (0.0019, 0.1689, –3.3462, –0.1670) 0.0981±j2.0026, –0.8763, –0.9875 不稳定指数2鞍焦 表 1 k=–1, 0和1时的平衡点及其特征值和稳定性
-
颜色 k=0.6 k=–0.5 吸引子类型 
(–10–6, 0, 0, 0) (0, –10–9, 0, 0) 周期吸引子 
(10–6, 0, 0, 0) (0, 10–9, 0, 0) 多周期吸引子 
(10–5, 0, 0, 0) (0, 10–7, 0, 0) 混沌吸引子 
(1, 0, 0, 0) (0, –2, 0, 0) 发散 
– (0, 5, 0, 0) 发散 表 2 图7中不同颜色吸引子对应的初值及吸引子类型
图共
9 个 表共
2 个