-
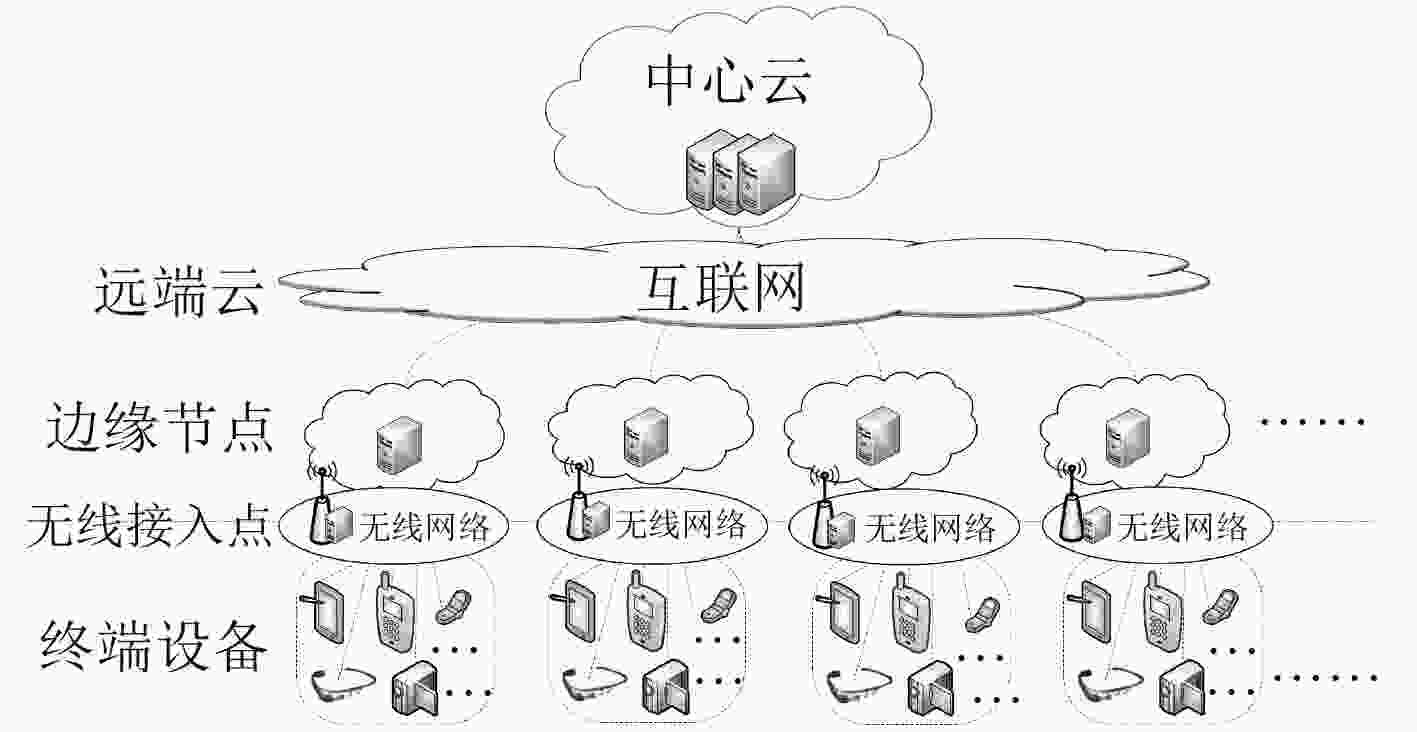
图 1 分层边缘云计算架构
Figure 1.
-
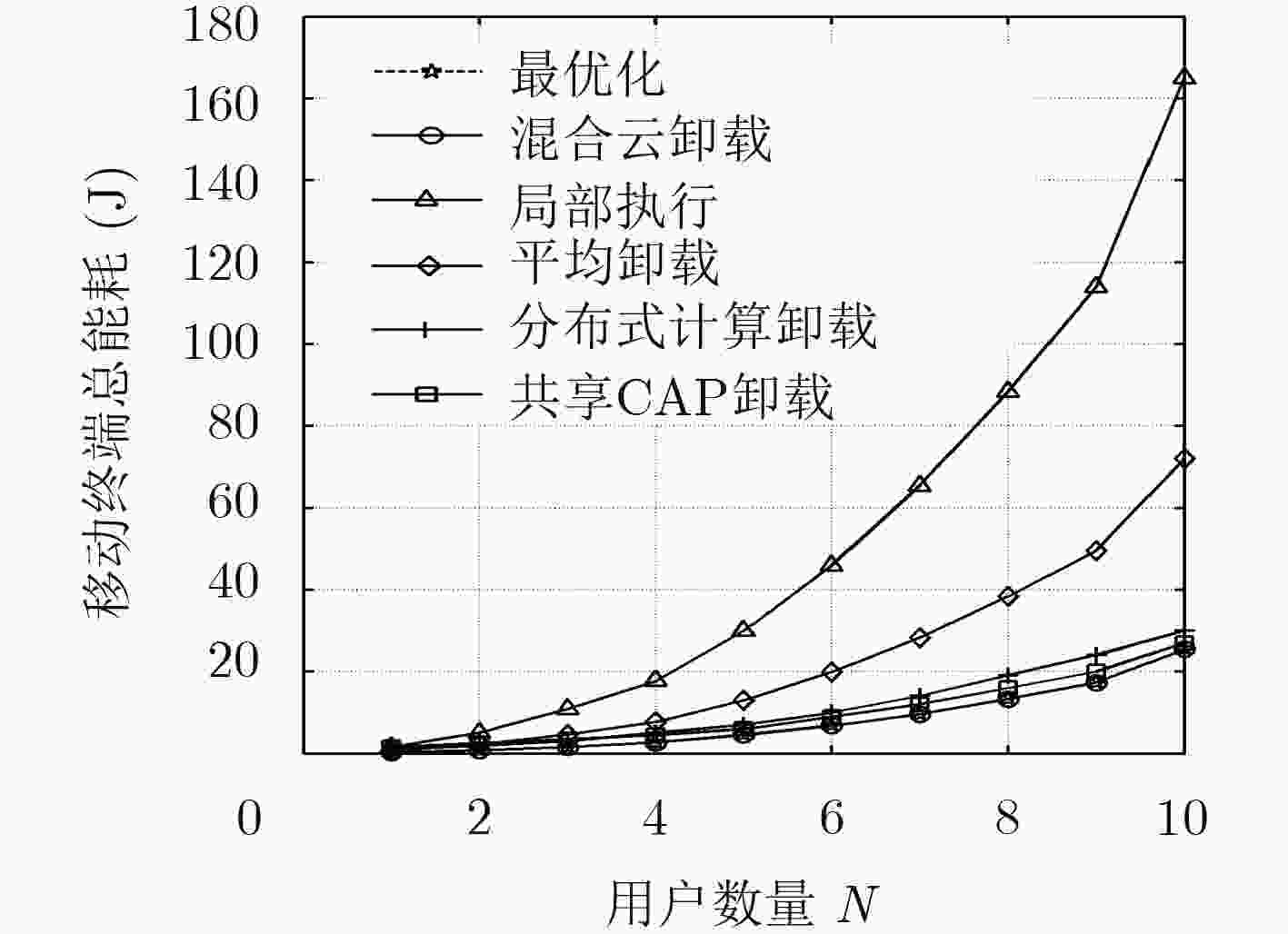
图 2 不同策略下移动终端总能耗变化
Figure 2.
-
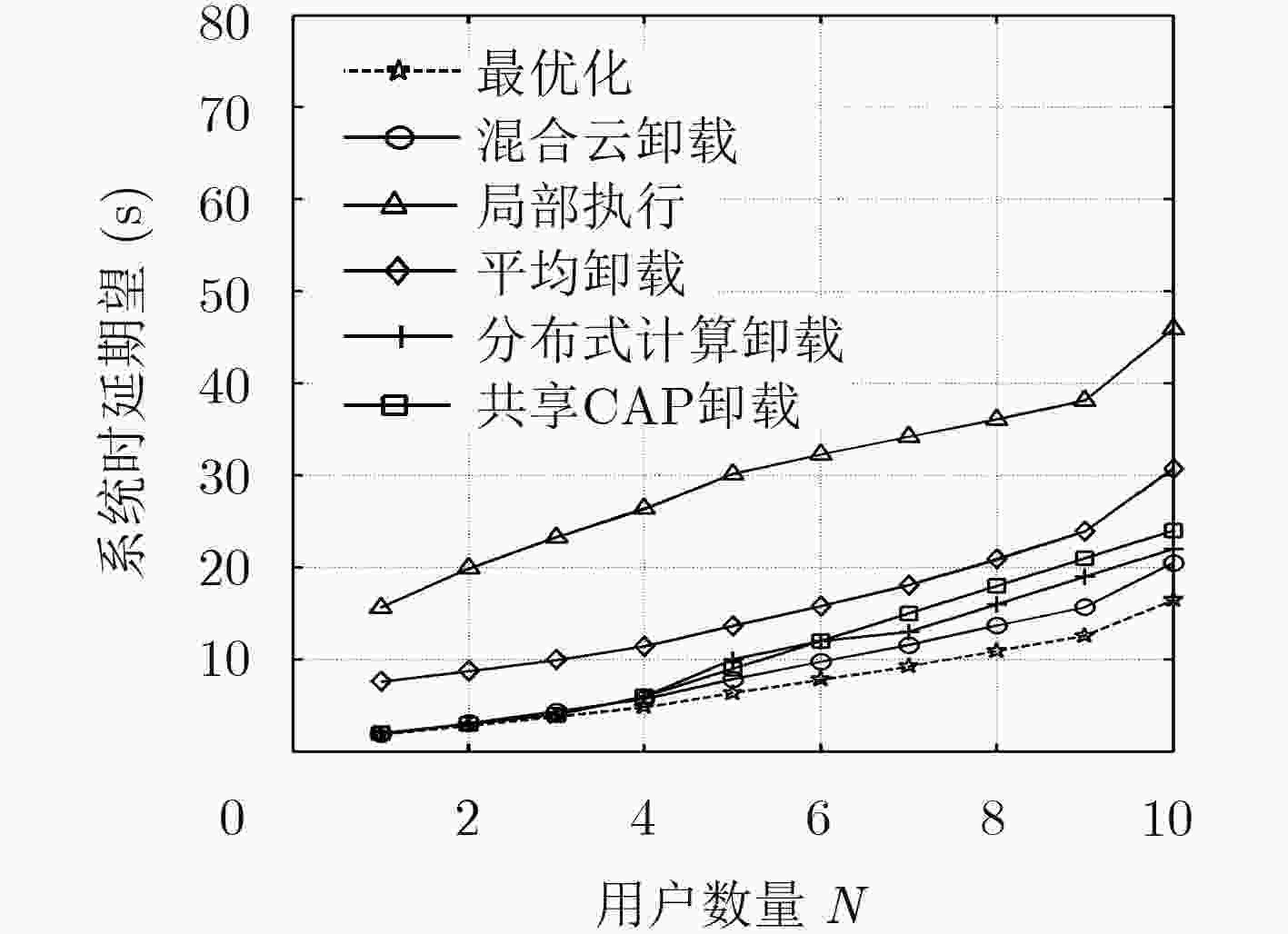
图 3 不同策略下系统时延期望变化
Figure 3.
-
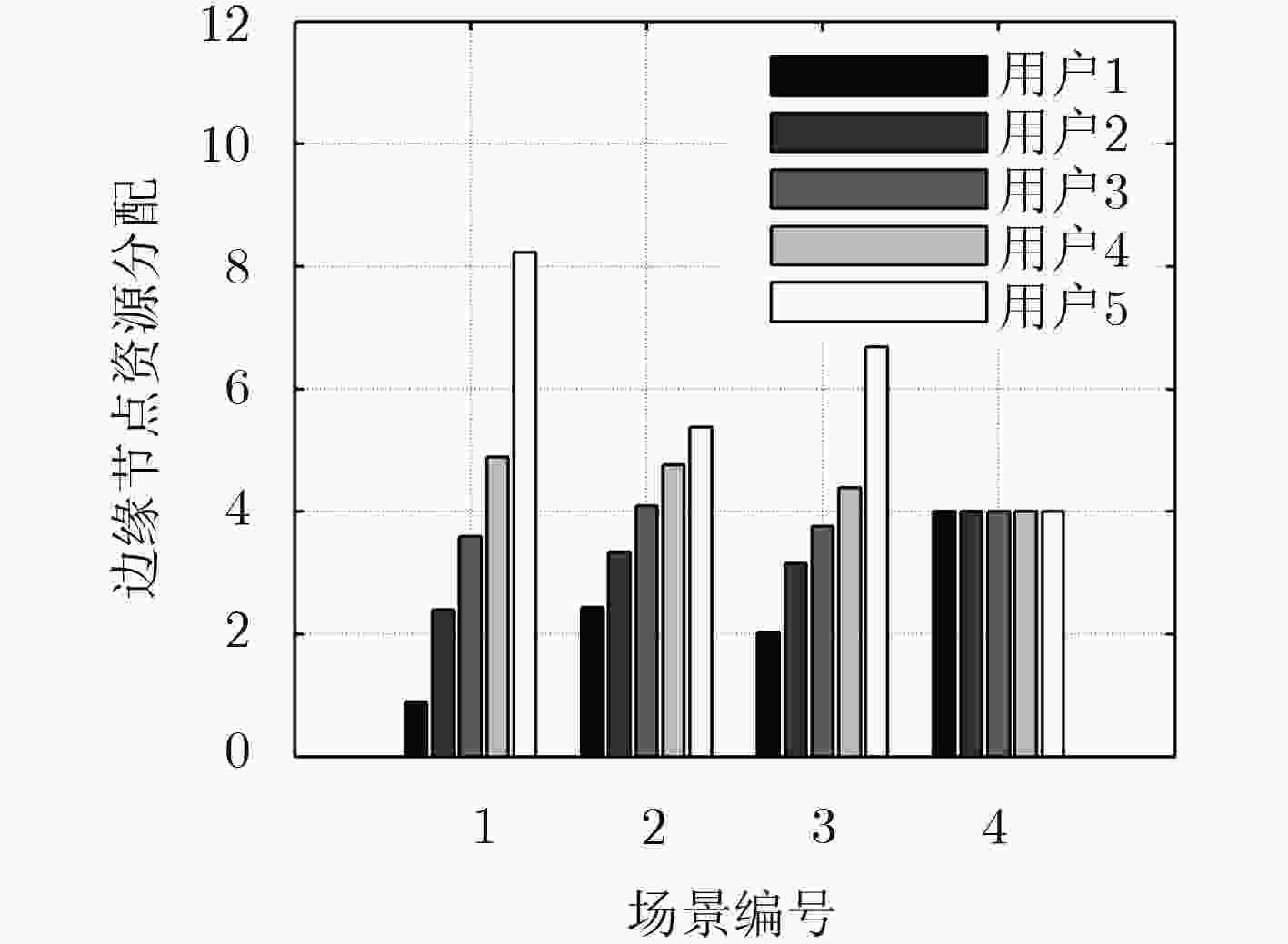
图 4 不同场景下边缘节点资源分配情况
Figure 4.
-
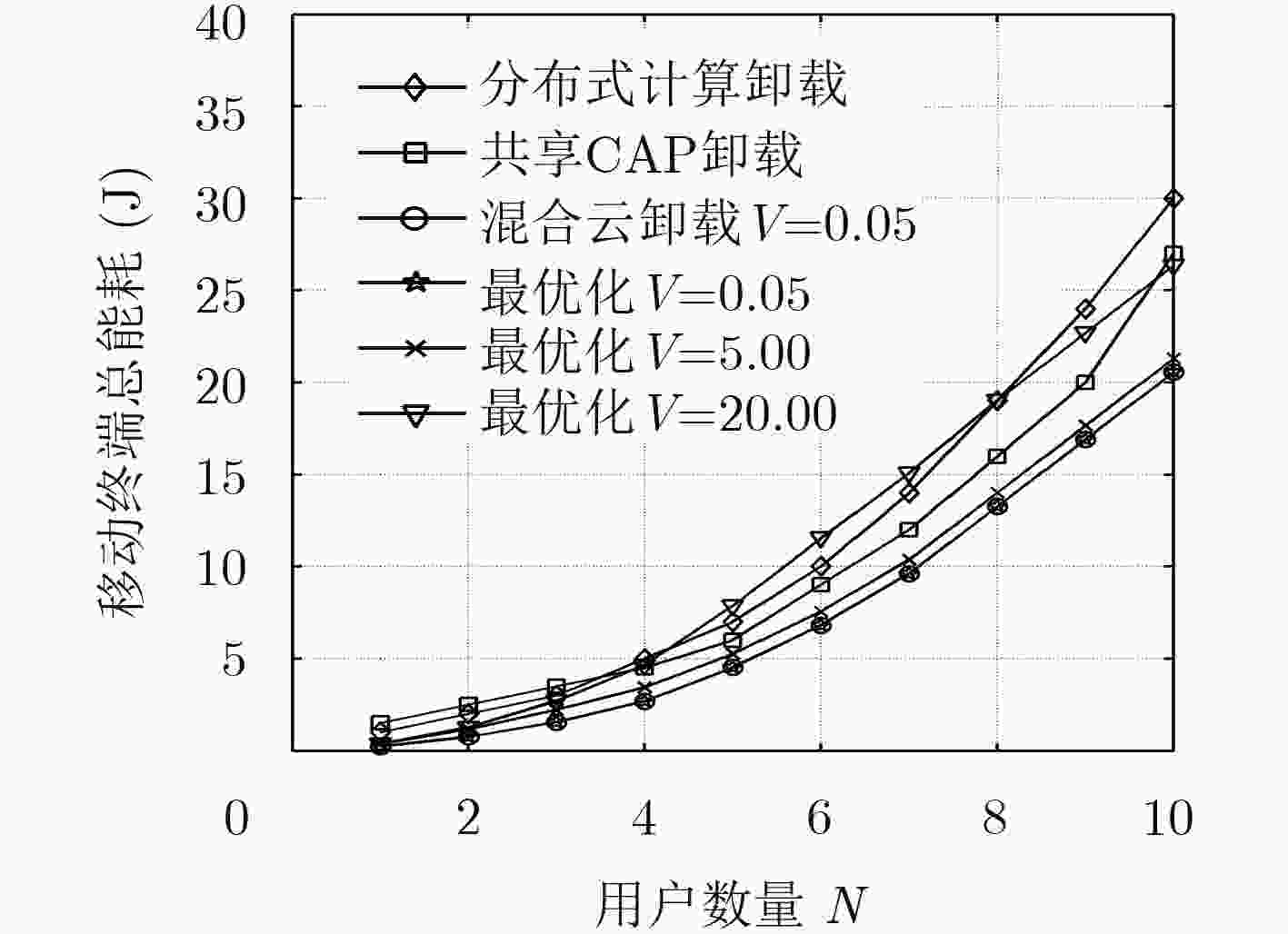
图 5 权重对移动终端总能耗的影响
Figure 5.
-
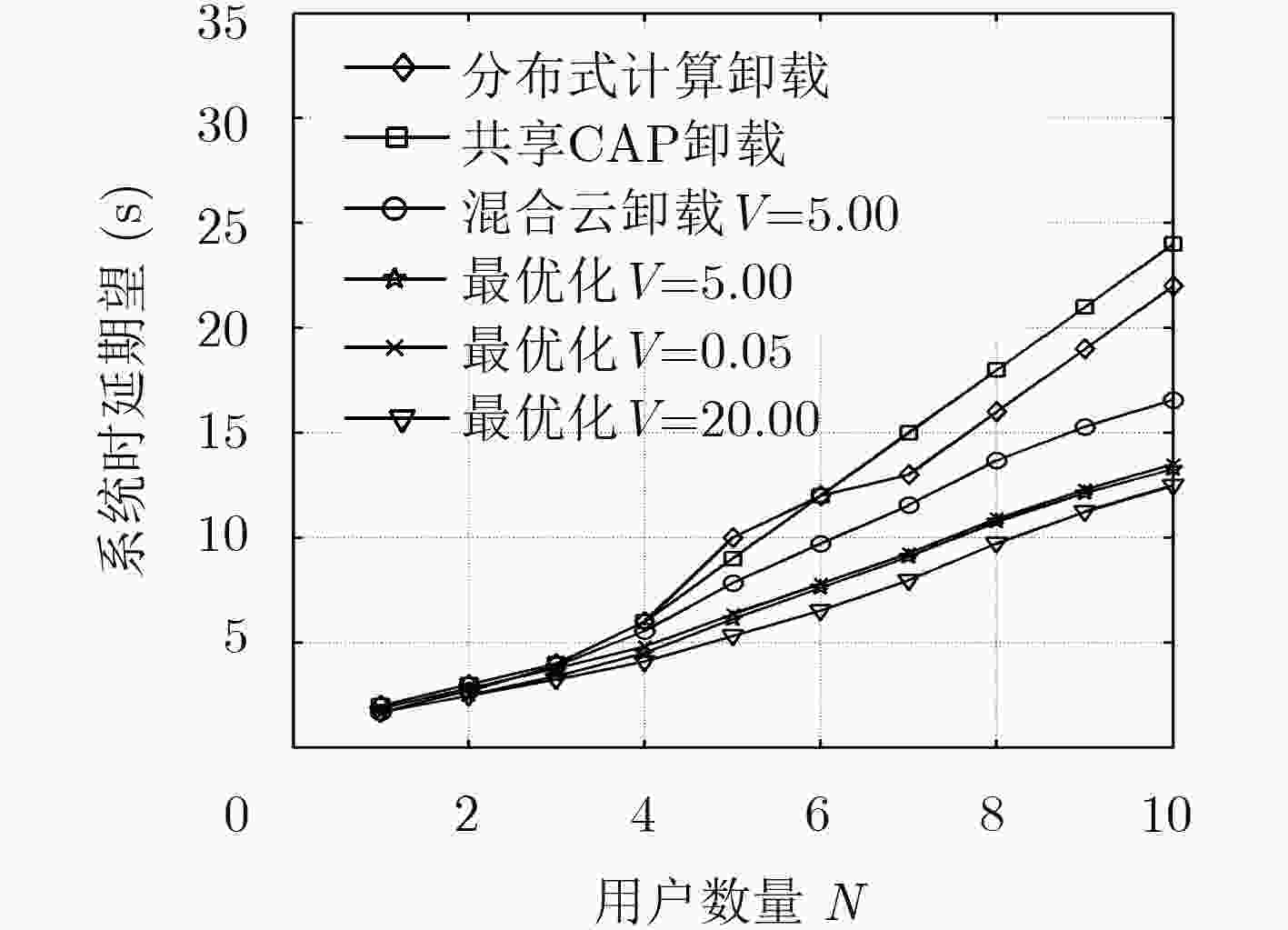
图 6 权值对系统时延期望的影响
Figure 6.
-
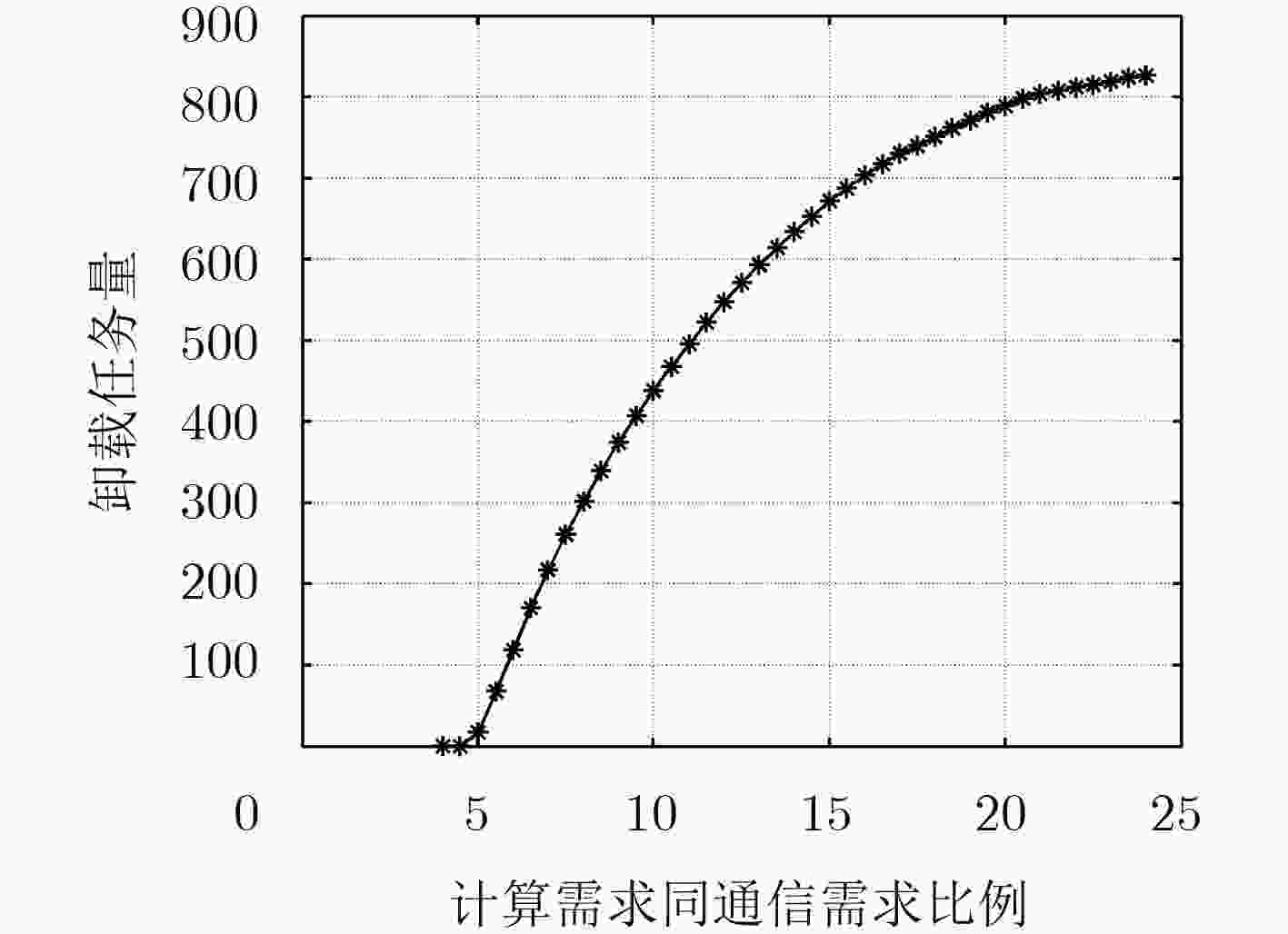
图 7 z的变化对卸载决策的影响
Figure 7.
-
初始化:各移动终端数量$n$及计算能力${C_i}$,边缘节点计算能力
${C_{{\rm{edge}}}}$,远端云节点计算能力${C_{{\rm{cloud}}}}$,无线带宽资源$B$,权值$V\,$, $S = \varnothing $;输入:各用户终端计算任务请求REQ($\left[ {{\lambda _1}, {\lambda _2}, ·\!·\!· , {\lambda _n}} \right]$); 输出:最优卸载决策$S = {X^*}$; $C_i^{{\ \rm{edge}}} = {{{C_{{\rm{edge}}}}} / n}$; while TRUE do; 接收用户计算卸载请求REQ,提取请求中的对应任务信息: $B_i^{{\rm{in}}}, {V_i}, B_i^{{\rm{out}}}, P_i^{\rm{c}}, P_i^{{\rm{up}}}, {\lambda _i}$; for each $i \in \left\{ {1, 2, ·\!·\!· , n} \right\}$ do; 引入拉格朗日函数,求得满足KKT条件的最优解
$ < {x_i}, x_i^{{\rm{edge}}}, x_i^{{\rm{cloud}}} > $;最优解向下取整,得整数解$ < x' + {1_i}, x_i^{'{\rm{edge}}}, x_i^{'{\rm{cloud}}} > $, $ < {x'_i}, x_i^{'{\rm{edge}}} + 1, x_i^{'{\rm{cloud}}} > $, $ < {x'_i}, x_i^{'{\rm{edge}}}, x_i^{'{\rm{cloud}}} + 1 > $; 将整数可行解代入目标函数,取使目标函数最小的整数解为最优 整数解; end for; 回传最优解${X^*}$,移动终端接收卸载决策,执行任务; end while. 表 1 多用户计算卸载
-
初始化:$n$, ${C_i}$, ${C_{{\rm{edge}}}}$, ${C_{{\rm{cloud}}}}$, $B$,权值$V\,$, $S = \varnothing $ 输入:各用户终端计算任务请求REQ($\left[ {{\lambda _1}, {\lambda _2}, ·\!·\!· , {\lambda _n}} \right]$) 输出:最优卸载决策$S = {X^*}$ $C_i^{{\ \rm{edge}}} = {{{C_{{\rm{edge}}}}} / n}$, ${C_0} = < C_1^{{\ \rm{edge}}}, C_2^{{\ \rm{edge}}}, ·\!·\!· , C_n^{{\ \rm{edge}}} > $; while TRUE do; 接收用户计算卸载请求REQ,提取任务信息:
$B_i^{{\rm{in}}}, {V_i}, B_i^{{\rm{out}}}, P_i^{\rm{c}}, P_i^{{\rm{up}}}, {\lambda _i}$;for each $i \in \left\{ {1, 2, ·\!·\!· , n} \right\}$ do; 引入拉格朗日函数,求得满足KKT条件的最优解
$ < {x_i}, x_i^{{\rm{edge}}}, x_i^{{\rm{cloud}}} > $;end for; 得到平均资源分配条件下的初始最优解${X^*}$, ${X_0} = {X^*}$; ${S_0} = < {X_0}, {C_0} > $; ${\mu ^{\left( 1 \right)}} = \left( {1, 1, ·\!·\!· , 1} \right)$, ${\eta ^{\left( 1 \right)}} = \left( {1, 1, ·\!·\!· , 1} \right)$, $\varepsilon = {10^{ - 5}}$, $M = 2$,
$\theta = 0.8$, $\alpha = 2$;$k = k + 1$; ${S_1} = {\rm{BFGS}}\left( {\varphi \left( {S, \mu , \eta , M} \right)} \right)$; ${\beta _k} = {\left\{ {\sum\limits_{i = 1}^n {{h_i}^2\left( {{S_k}} \right)} + \sum\limits_{j = 1}^{4n + 1} {{{\left[ {\left( {\min {g_j}\left( {{S_k}} \right), \frac{{{{\left( {{\eta ^{\left( K \right)}}} \right)}_j}}}{M}} \right)} \right]}^2}} } \right\}^{{1 / 2}}}$; while ${\beta _k} > \varepsilon $ do; 更新罚函数:若${\beta _k} > \theta \cdot {\beta _k}$,则$M = \alpha \cdot M$,否则$M$不变; 更新乘子向量${\mu ^{\left( k \right)}}$, ${\eta ^{\left( k \right)}}$; $k = k + 1$; ${S_k} = {\rm{BFGS}}\left( {\varphi \left( {S, \mu , \eta , M} \right)} \right)$; 依据上述公式计算${\beta _k}$值; end while; 对$ < {x_i}, x_i^{{\rm{edge}}}, x_i^{{\rm{cloud}}} > $求最优整数解,返回${S_k}^* = < {X_k}^*, {C_k}^* > $,
按${X_k}^*$进行计算卸载,按${C_k}^*$进行计算资源分配;end while. 表 2 多用户计算卸载及资源分配机制
图共
7 个 表共
2 个