-
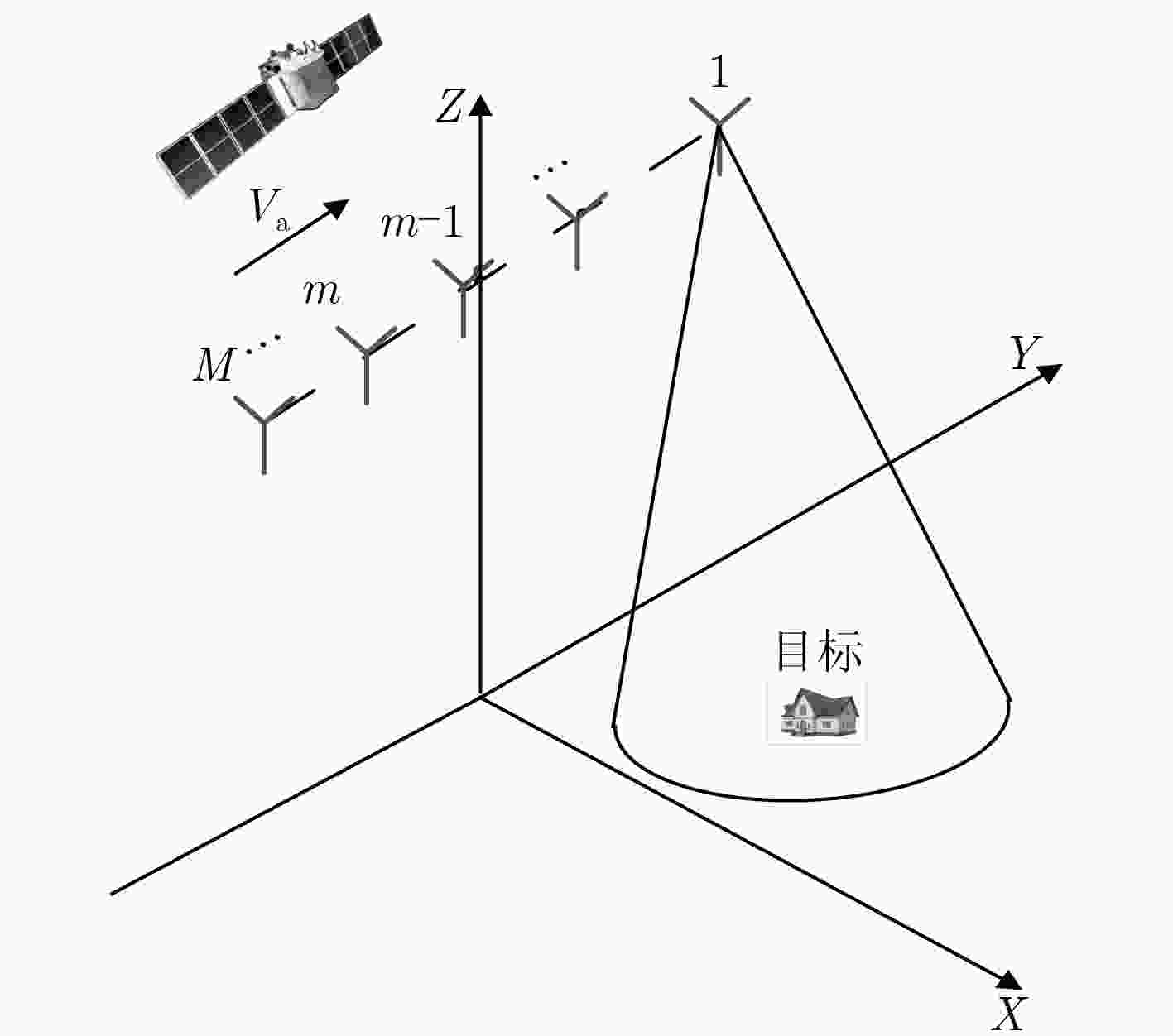
图 1 方位向多通道星载SAR系统空间几何关系图
Figure 1.
-
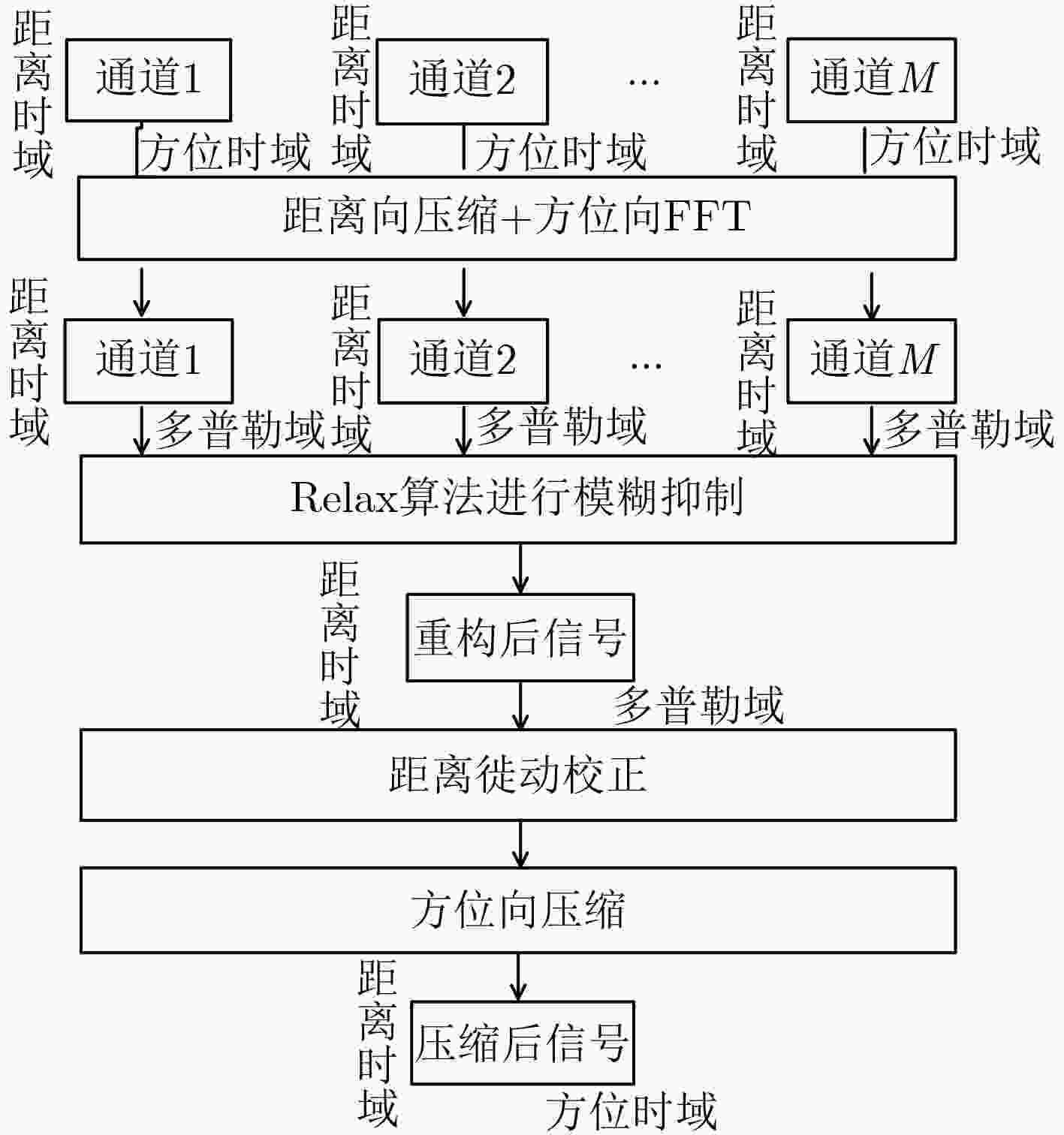
图 2 方位向多通道星载SAR系统成像处理流程
Figure 2.
-
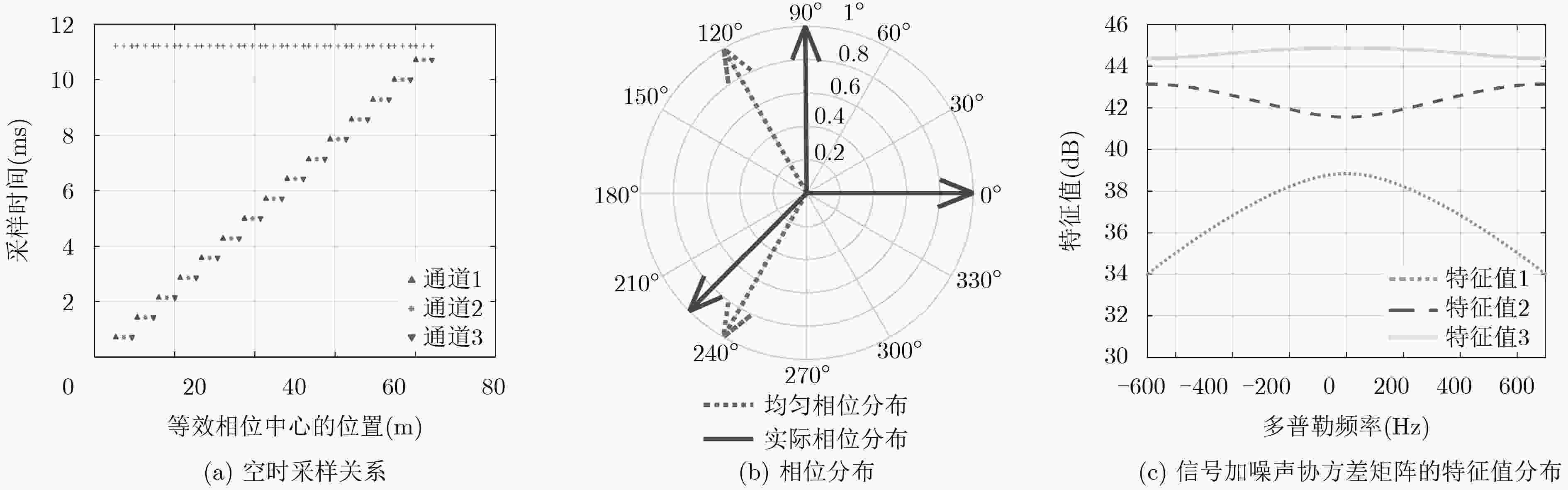
图 3 空时采样关系、相位分布以及信号加噪声协方差矩阵的特征值分布结果
Figure 3.
-

图 4 仿真的距离-多普勒域回波信号
Figure 4.
-
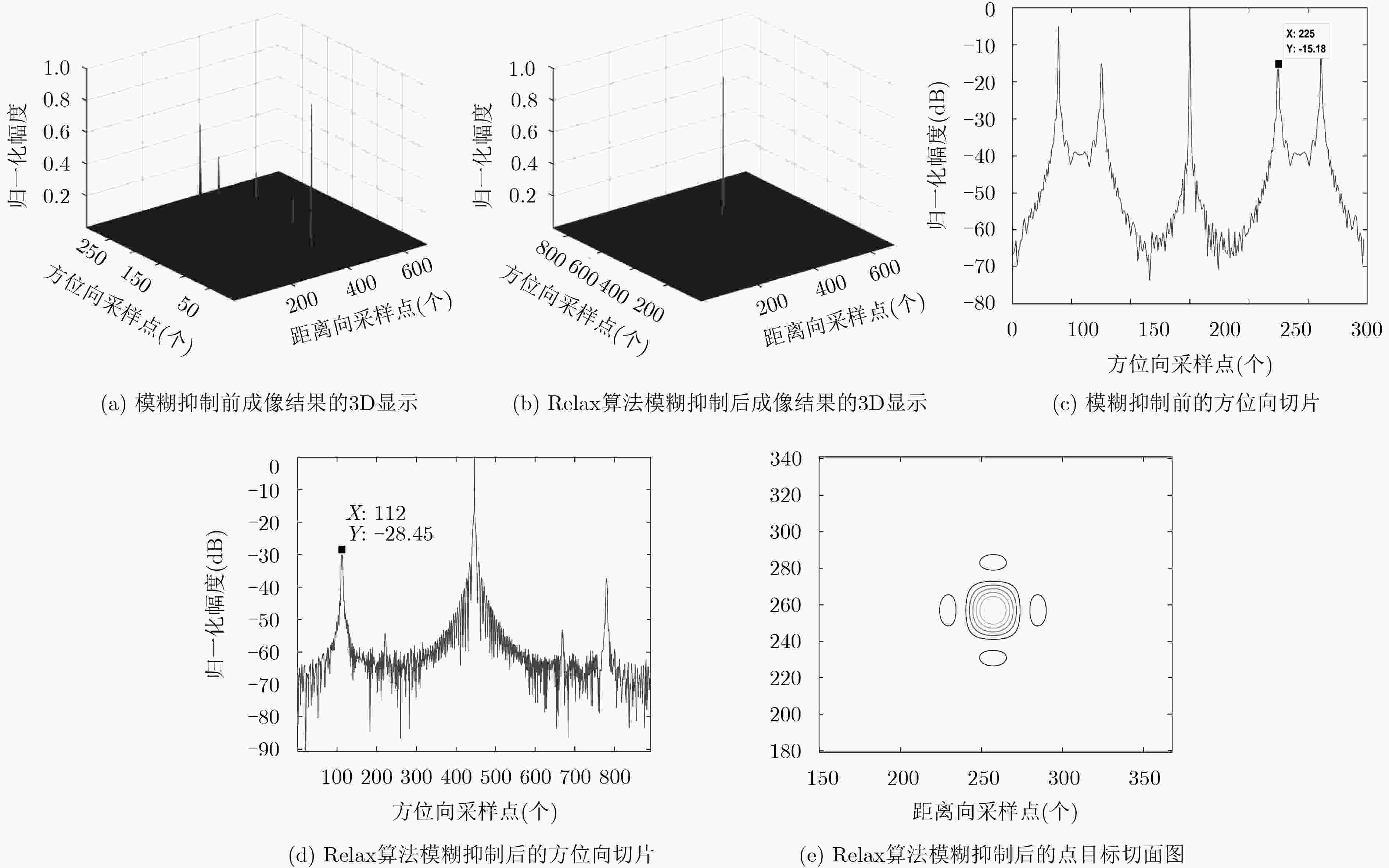
图 5 方位压缩后的成像结果
Figure 5.
-
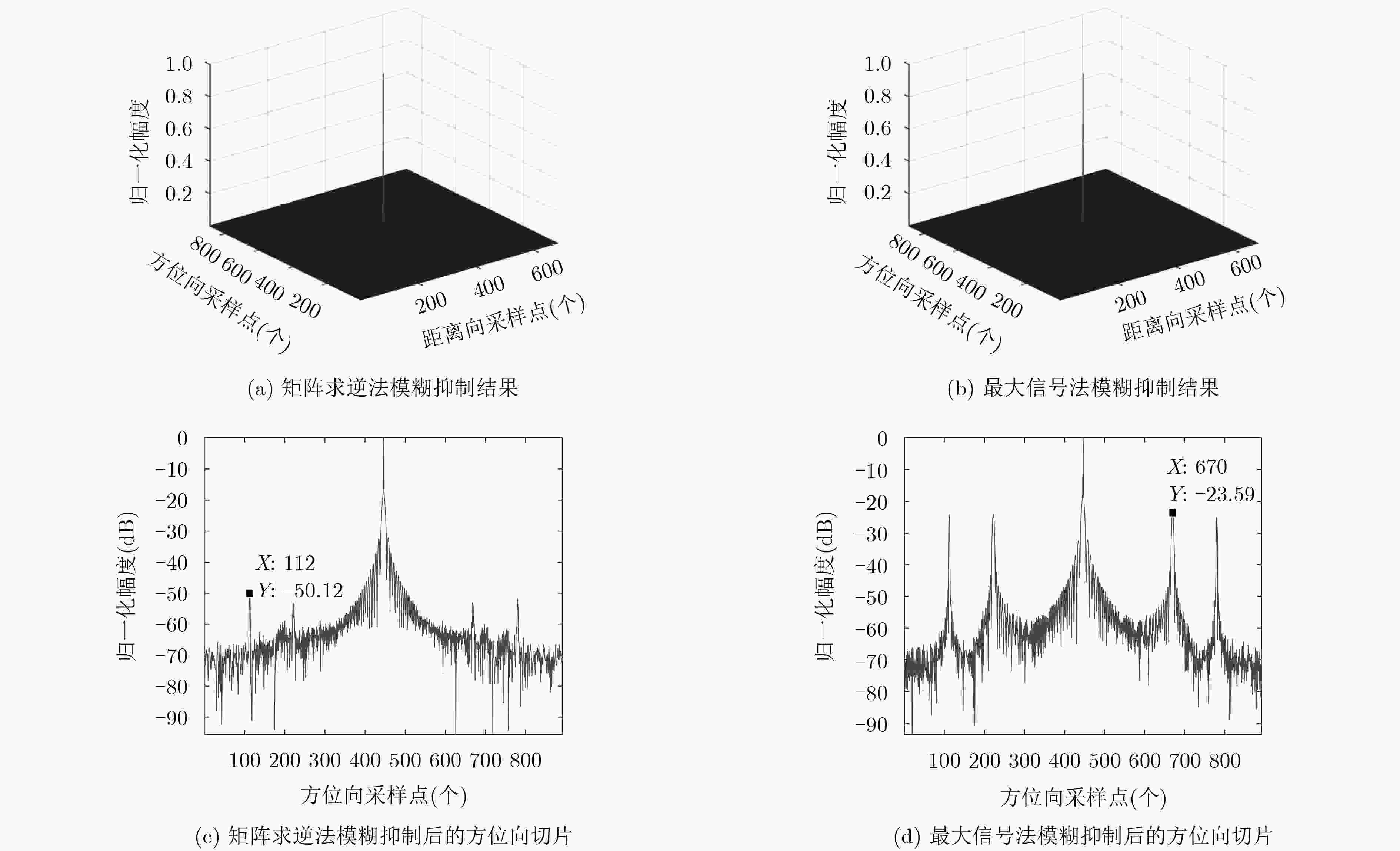
图 6 矩阵求逆法和最大信号法的信号重建结果
Figure 6.
-
符号 说明 $M$ 通道个数 $r$ 距离变量,$r = {\rm c}t/2$ c 光速 $t$ 距离向时间变量 ${f_{\rm d}}$ 多普勒频率 $\vartheta $ 目标参数向量,$\vartheta = {[{T_0}, {R_0}, {\sigma ^2}, \varTheta ]^{\rm{T}}}$ ${T_0}$ 最小斜距对应的时间 ${R_0}$ 最小斜距$\min \{ R(T\,)\} = R({T_0}) = {R_0}$ ${\sigma ^2}$ 目标功率 $\varTheta $ 目标相位 ${f\!_{p}}$ 各通道的脉冲重复频率 $\varOmega $ 2次相位项的变化率 $R(T\,)$ 雷达与目标之间的距离 $T\,$ 慢时间变量 ${{u}}[{f_{\rm d}}, \vartheta ]$ 天线与目标间的瞄准线向量 ${A_m}$ 第$m$个通道的双向天线方向图 ${d_m}$ 第$m$个通道的等效相位中心 表 1 公式中用到的符号说明
-
For $m = 1: \rm Na$ For $n = 1:{\rm Nr}$
%遍历所有距离-多普勒单元(其中,$\rm Na$表示多普勒单元的个数,
$\rm Nr$表示距离单元的个数)
${Z_{{\rm{rec_{-}1}}}}(r, {f_{\rm d}} + p{f\!_{p}}) = \frac{{{{a}}_p^{\rm{H}}\left( {{f_{\rm d}}} \right){{Z}}\left( {r, {f_{\rm d}}} \right)}}{M}$ %初始化操作
%第1次迭代
$\begin{align}{{{Z}}_{p_{-}1}}\left( {r, {f_{\rm d}}} \right) =& {{Z}}\left( {r, {f_{\rm d}}} \right) \\&- \sum\limits_{i = - \left( {M - 1} \right)/2, i \ne p}^{\left( {M - 1} \right)/2} {{{{a}}_i}\left( {{f_{\rm d}}} \right)} \cdot {Z_{{\rm{rec_{-}1}}}}\left( {r, {f_{\rm d}} + p{f\!_{p}}} \right)\end{align}$
${\hat Z_{{\rm{rec_{-}1}}}}\left( {r, {f_{\rm d}} + p{f\!_{p}}} \right) = \frac{{{{a}}_p^{\rm{H}}\left( {{f_{\rm d}}} \right){{{Z}}_{p_{-}1}}\left( {r, {f_{\rm d}}} \right)}}{M}$
如果未满足收敛条件或者未达到迭代次数
%第$k$次迭代($k \ge 2$)
$\begin{align}{{{Z}}_{p_{-}k}}\left( {r, {f_{\rm d}}} \right) =& {{Z}}\left( {r, {f_{\rm d}}} \right) \\& - \sum\limits_{i = - \left( {M - 1} \right)/2, i \ne p}^{\left( {M - 1} \right)/2} {{{{a}}_i}\left( {{f_{\rm d}}} \right)} \cdot {\hat Z_{{{{\rm rec}_{-}k - 1}}}}\left( {r, {f_{\rm d}} + p{f\!_{p}}} \right)\end{align}$
${\hat Z_{{{{\rm rec}_{-}k}}}}\left( {r, {f_{\rm d}} + p{f\!_{p}}} \right) = \frac{{{{a}}_p^{\rm{H}}\left( {{f_{\rm d}}} \right){{{Z}}_{p_{-}k}}\left( {r, {f_{\rm d}}} \right)}}{M}$
End
End
End表 2 基于Relax算法的模糊抑制
-
算法类别 PSLR(dB) 方位向分辨率(m) SNR(dB) SANR(dB) 矩阵求逆法 13.99 1.66 39.46 27.08 最大信号法 13.99 1.66 40.33 12.97 Relax法 13.82 1.66 50.56 21.22 表 3 不同重建方法的性能对比
图共
6 个 表共
3 个