-
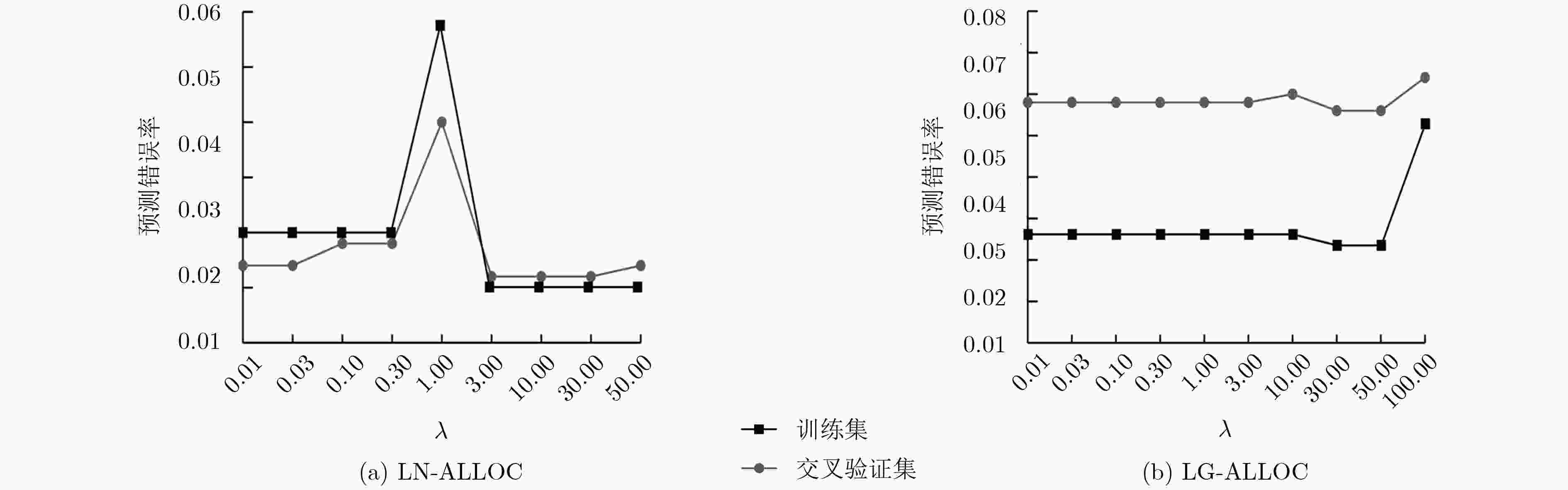
图 1 两种算法预测错误率与参数
$\lambda $ 变化关系Figure 1.
-
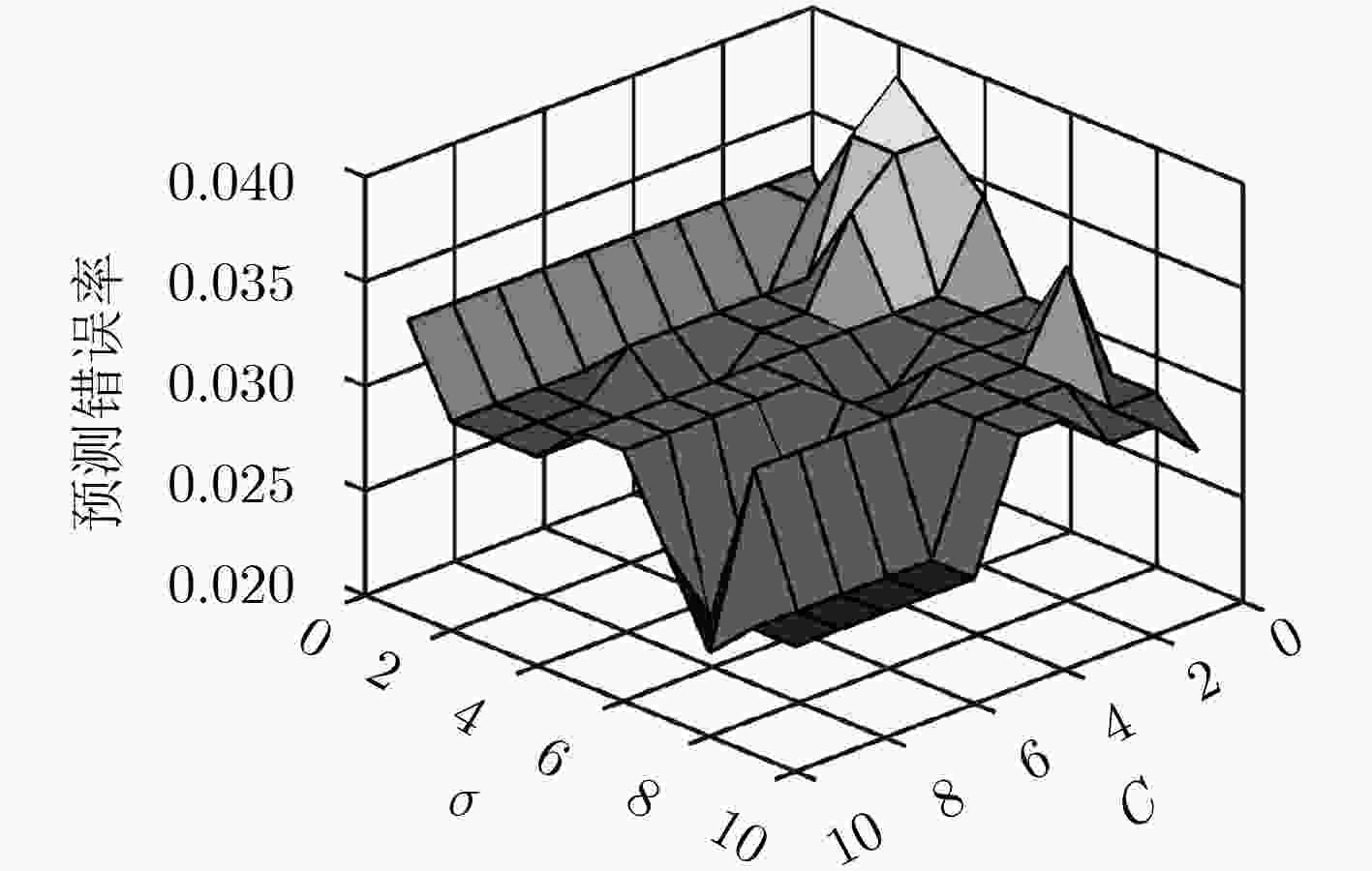
图 2 SVM-ALLOC预测错误率与参数C及
$\sigma $ 变化关系Figure 2.
-

图 3 3种监督学习算法的训练时间
Figure 3.
-
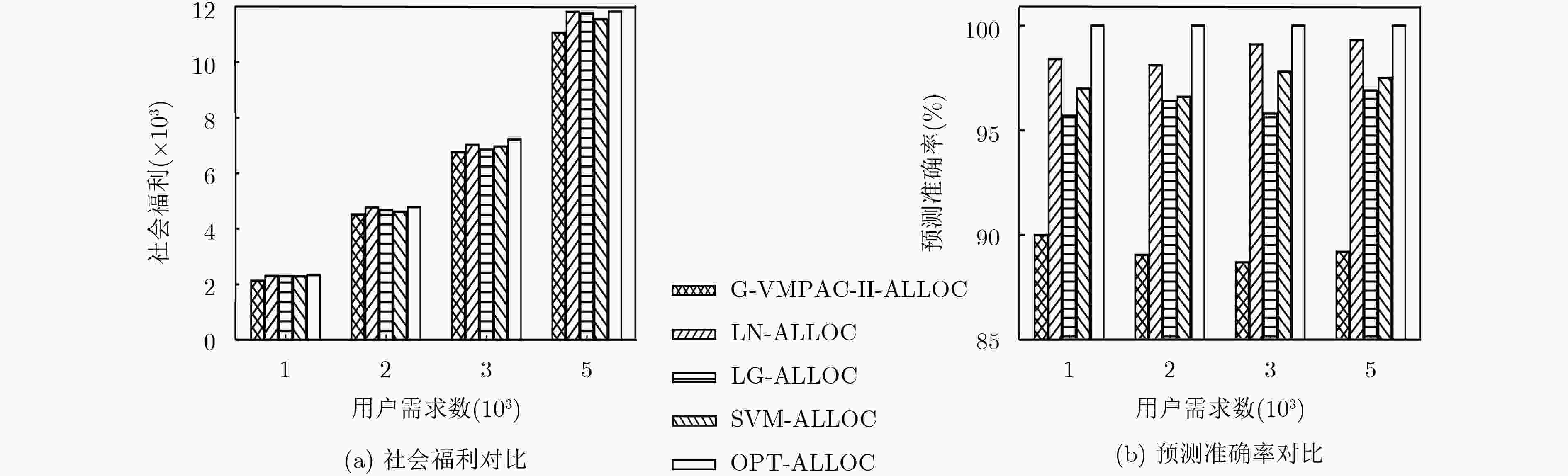
图 4 不同分配算法求解社会福利与预测准确率对比
Figure 4.
-
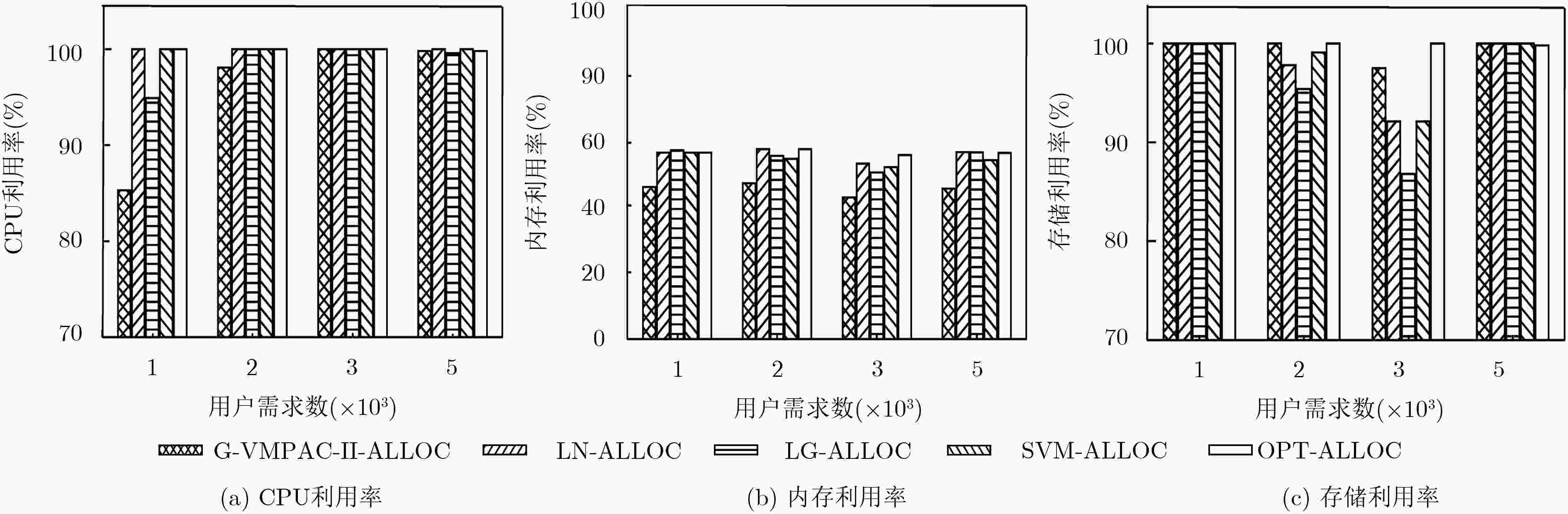
图 5 不同分配算法资源利用率对比
Figure 5.
-
输入 所有用户的需求信息集:${R} = \{ R_{}^{(1)}\,R_{}^{(2)}\, ·\!·\!· \,R_{}^{(m)}\} $ 监督学习算法对资源分配的预测结果:
${PD} = ({\rm{pd}}_{}^{(1)}\,{\rm{pd}}_{}^{(2)}\, ·\!·\!· \,{\rm{pd}}_{}^{(m)})$每类虚拟资源的容量:${C} = ({c_1}\;\;\;{c_2}\;\;\; ·\!·\!· \;\;\;{c_n})$ 输出 被选中的用户需要支付的价格,
${Pay} = ({\rm pay}_{}^{(1)}\,{\rm{pay}}_{}^{(2)}\, ·\!·\!· \,{\rm{pay}}_{}^{(m)})$(1) ${{PD}^{\rm{*}}} \leftarrow 0$ (2) $\delta \leftarrow {10^{{\rm{ - }}6}}$ (3) for each $i \leftarrow \{ i|{\rm{pd}}_{}^{(i)} \in {PD}, {\rm{pd}}_{}^{(i)}{\rm{ = 1}}\} $ do (4) ${\rm{pay}}_{}^{(i)} \leftarrow b_{}^{(i)};{\rm{pay}}_{}^{(i)'} \leftarrow 0\;\;\;\;;\;\;\;b_{}^{(i)} \leftarrow ({\rm{pay}}_{}^{(i)} + {\rm{pay}}_{}^{(i)'})/2$ (5) while (${\rm{|pay}}_{}^{(i)}{\rm{ - pay}}_{}^{(i)'}{\rm{| > }}\delta $) do (6) 运行LN-ALLOC, LG-ALLOC或SVM-ALLOC求解
出新的资源分配解${P}{{D}^{\rm{*}}}$(7) if ${\rm{pd}}_{}^{(i)}{\rm{ = }}1\;\;\;,{\rm{pd}}_{}^{(i)} \in {P}{{D}^{\rm{*}}}$ (8) ${\rm{pay}}_{}^{(i)} \leftarrow b_{}^{(i)};b_{}^{(i)} \leftarrow ({\rm{pay}}_{}^{(i)} + {\rm{pay}}_{}^{(i)'})/2$ (9) else (10) ${\rm{pay}}_{}^{(i)'} \leftarrow b_{}^{(i)};b_{}^{(i)} \leftarrow ({\rm{pay}}_{}^{(i)} + {\rm{pay}}_{}^{(i)'})/2$ (11) end if (12) end while (13) ${Pay} \leftarrow {Pay} \cup {\rm{pay}}_{}^{(i)}$ (14) end for (15) return ${Pay}$ 表 1 基于临界值的价格计算算法(CV-PAY)
图共
5 个 表共
1 个

