-
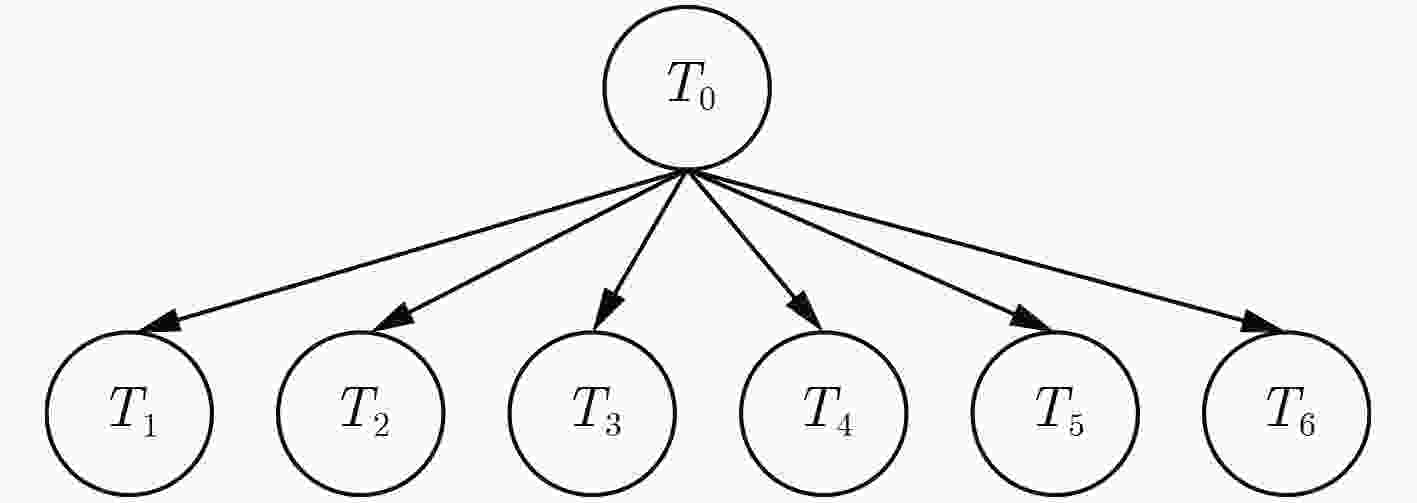
图 1 任务示例图
Figure 1.
-
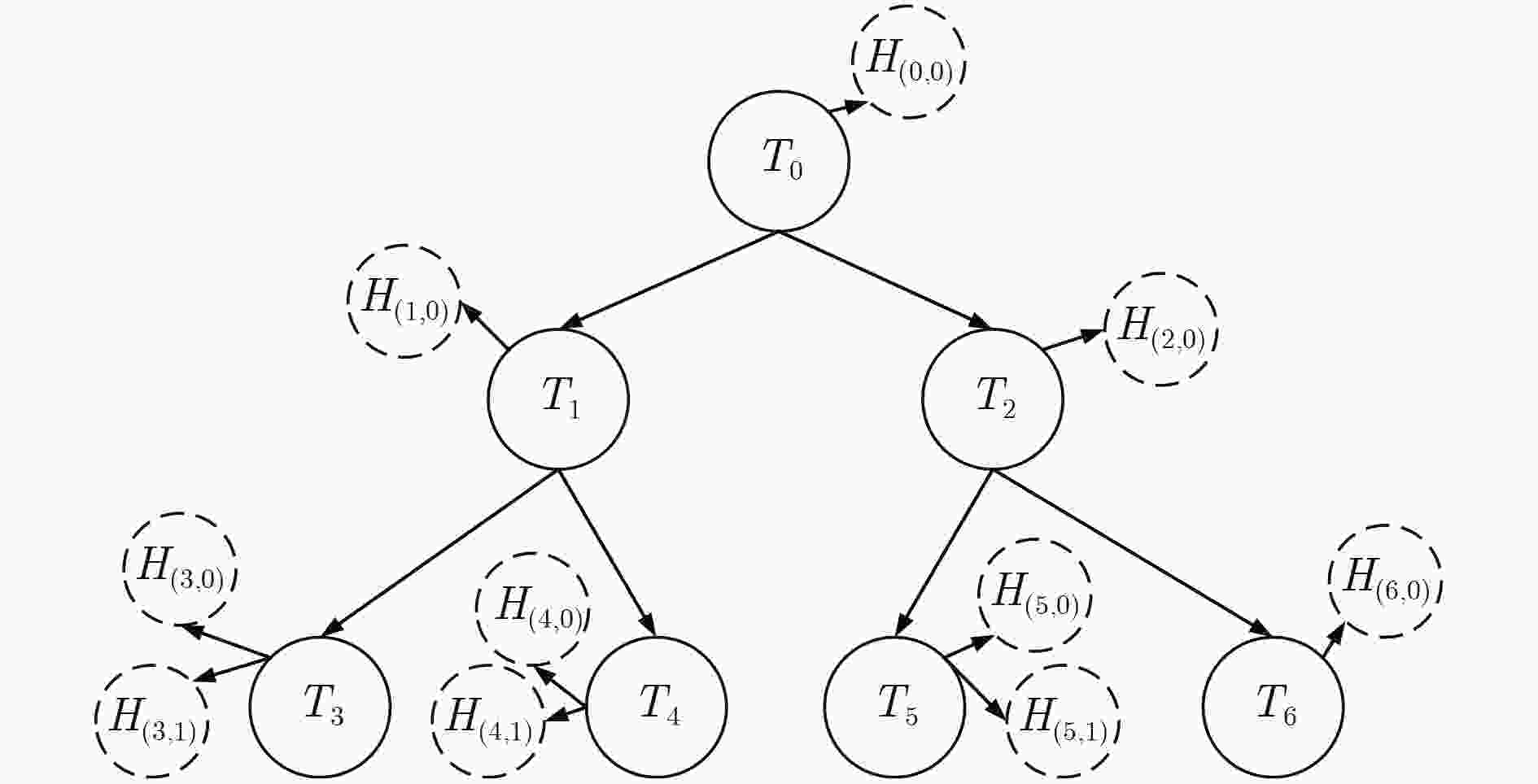
图 2 扩展的任务示例图
Figure 2.
-
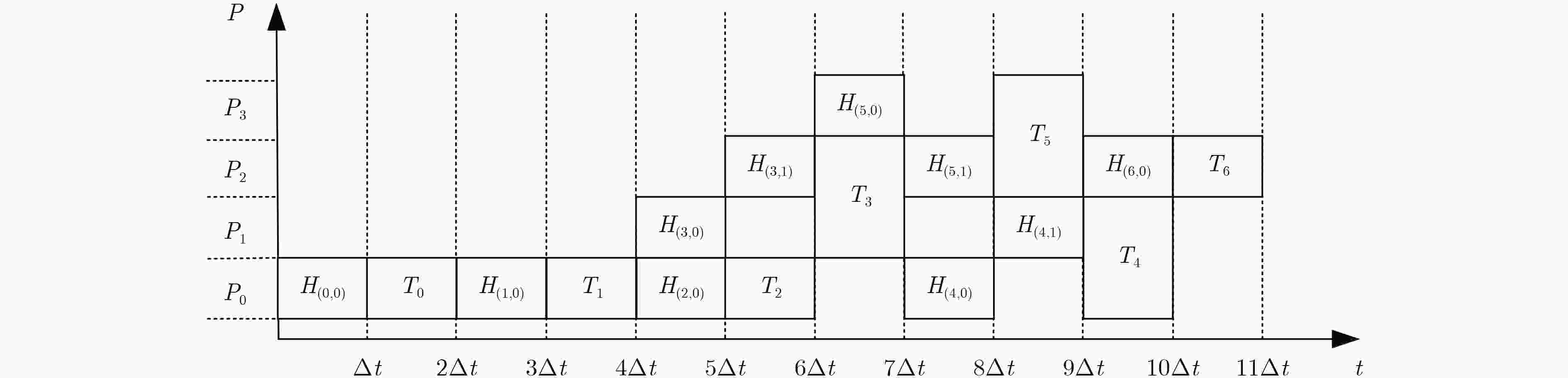
图 3 任务映射时序图
Figure 3.
-
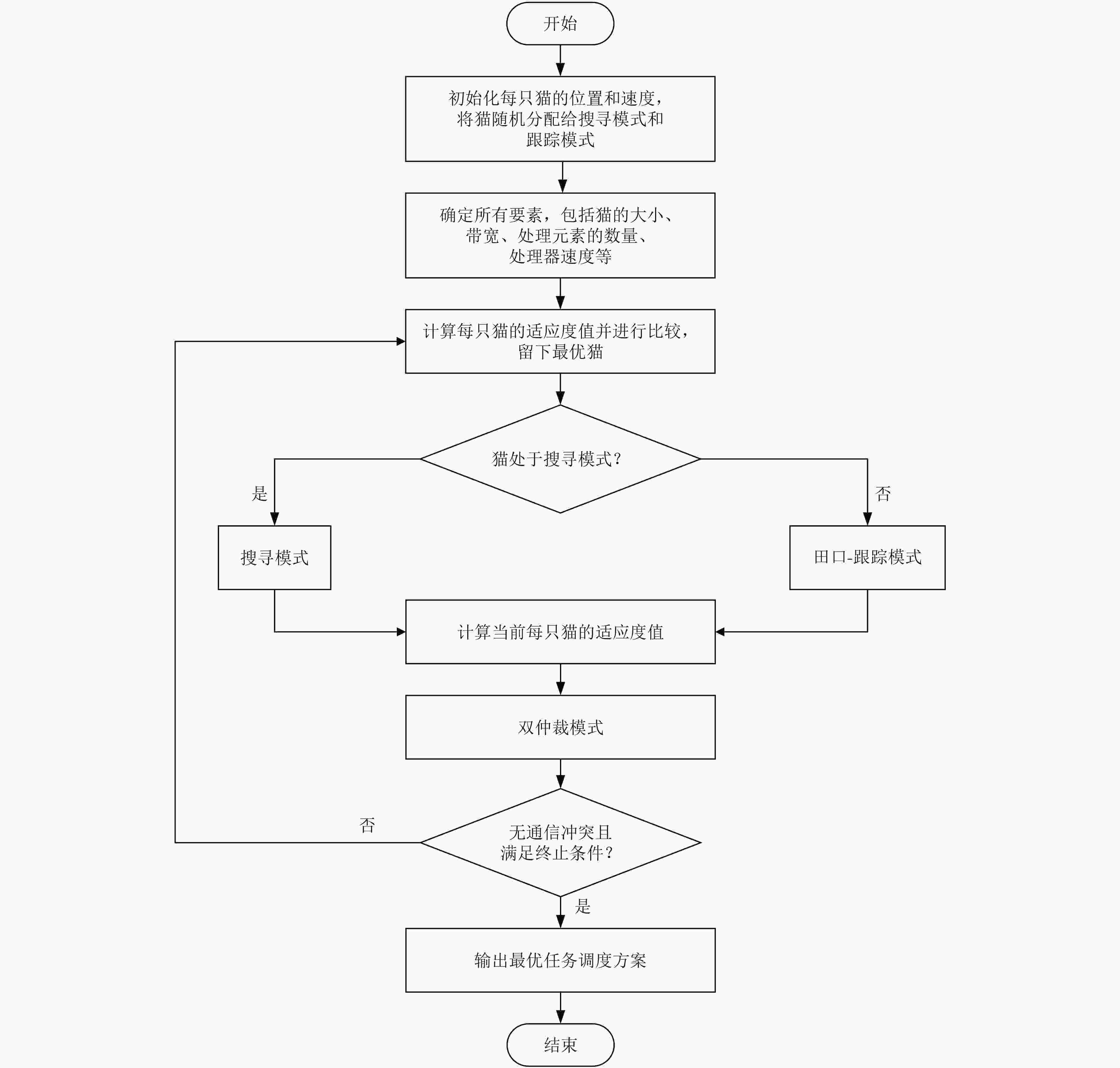
图 4 DTCSO算法流程图
Figure 4.
-
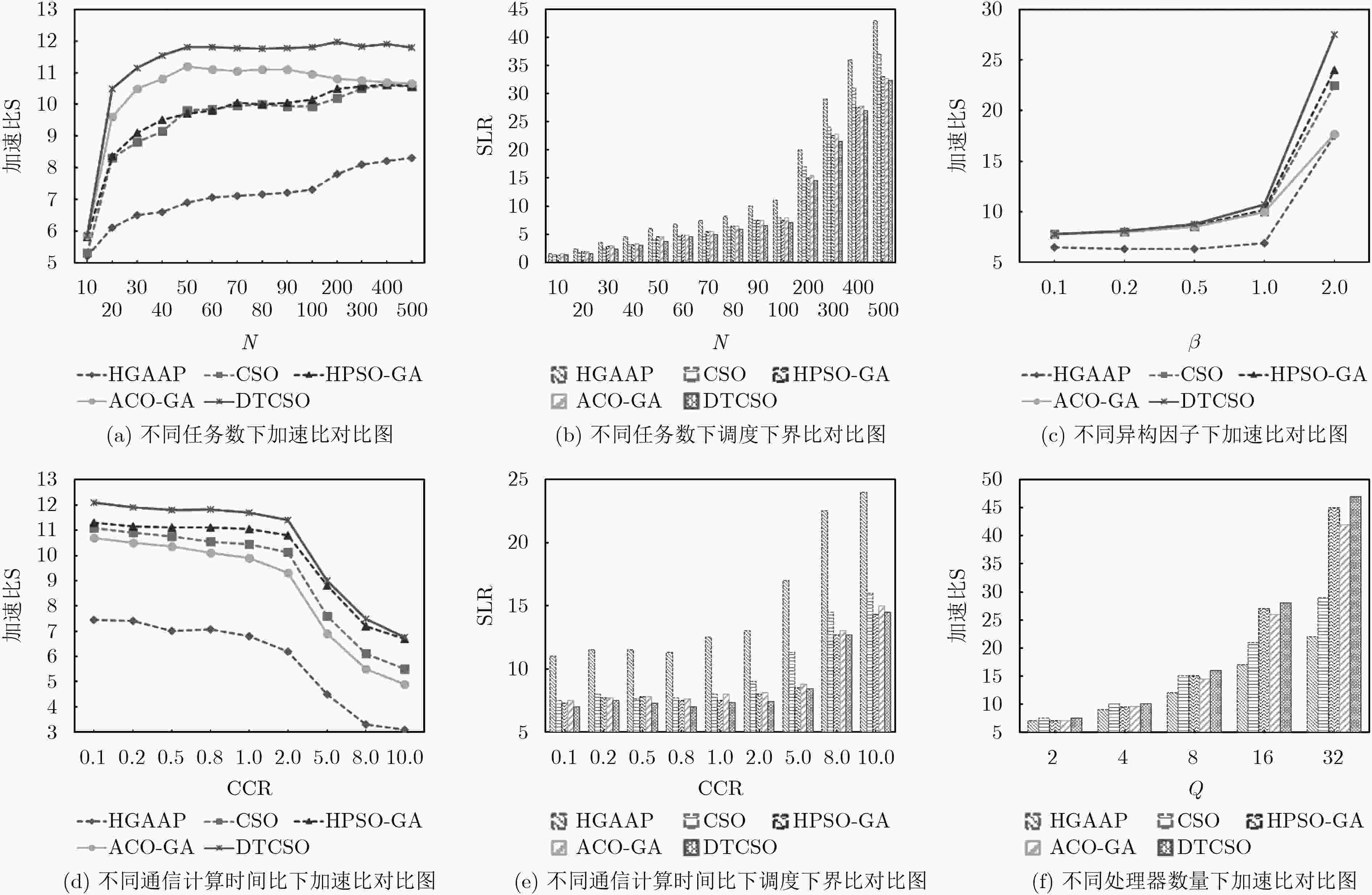
图 5 算法性能对比图
Figure 5.
-
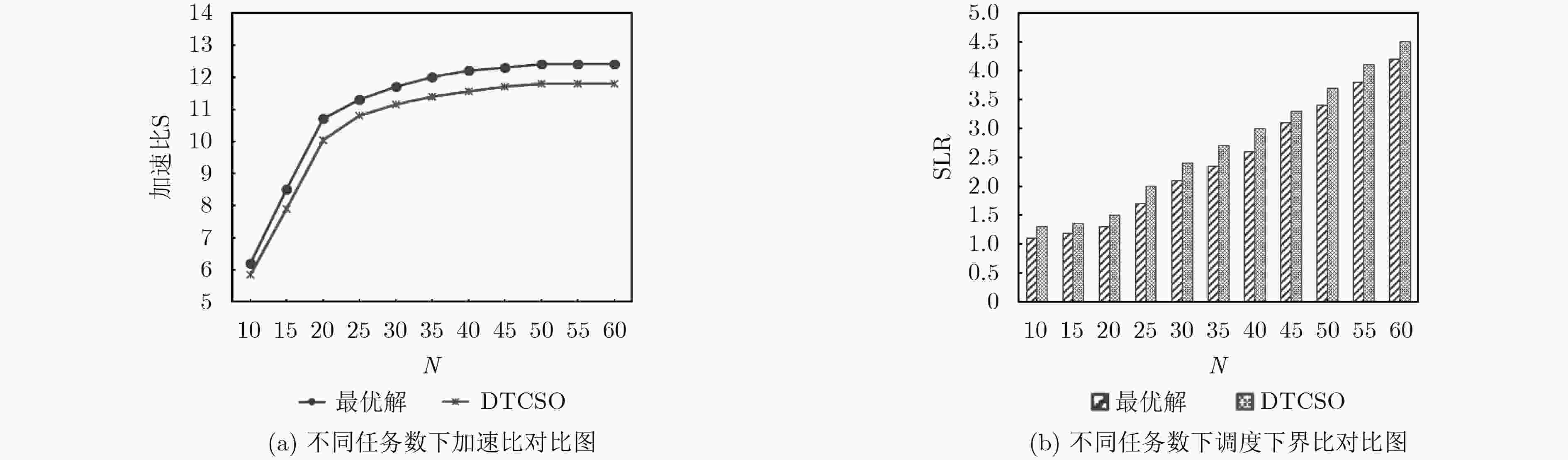
图 6 DTCSO算法与最优解对比图
Figure 6.
-
算法1 双仲裁映射判决算法 输入:TA, PLA, t, Tm 输出:有效的任务映射结果DAM(T) (1) if (( ${T_m} \cdot {t_a} \le t \le {T_m} \cdot {t_s}$) and ( ${T_m} \cdot s = {\rm IDLE}\parallel {\rm WAIT}$)) then
enQueue (Q, Tm)(2) Select Tm from Q where ${T_m} \cdot p$ is the highest (3) if (PLA=NULL) then (4) temp P·taskid $ \leftarrow {T_n} \cdot \rm{taskid}$;
temp P·pos $ \leftarrow {[(0},{0),(}{T_n} \cdot w,{T_n} \cdot h{)]}$;(5) ${T_n} \cdot s \leftarrow {\rm EXE}$;TA [i+1][0] $ \leftarrow {T_n} \cdot w$; TA [i+1][1] $ \leftarrow {T_n} \cdot h$; (6) insert node tempP into PLA; else (7) DAM(Tj, d); end if (8) end if 表 1 双仲裁映射判决算法
-
实验序列号 考虑的因子 A B C D E F G 1 1 0 0 1 1 0 0 2 1 1 1 0 0 0 0 3 0 0 1 0 1 1 0 4 0 1 0 0 1 0 1 5 1 1 1 1 1 1 1 6 1 0 0 0 0 1 1 7 0 0 1 1 0 0 1 8 0 1 0 1 0 1 0 表 2 L8(27)正交阵列
-
T0 T1 T2 T3 T4 T5 T6 P0 T0/P0 T1/P0 T2/P0 T3/P0 T4/P0 T5/P0 T6/P0 P1 T0/P1 T1/P1 T2/P1 T3/P1 T4/P1 T5/P1 T6/P1 P2 T0/P2 T1/P2 T2/P2 T3/P2 T4/P2 T5/P2 T6/P2 P3 T0/P3 T1/P3 T2/P3 T3/P3 T4/P3 T5/P3 T6/P3 P4 T0/P4 T1/P4 T2/P4 T3/P4 T4/P4 T5/P4 T6/P4 P5 T0/P5 T1/P5 T2/P5 T3/P5 T4/P5 T5/P5 T6/P5 P6 T0/P6 T1/P6 T2/P6 T3/P6 T4/P6 T5/P6 T6/P6 P7 T0/P7 T1/P7 T2/P7 T3/P7 T4/P7 T5/P7 T6/P7 表 3 预估计算时间矩阵
-
算法2 田口-猫群优化算法 输入:猫的初始位置,初始速度,MR, SMP, SRD, CDC, SPC
输出:最优的任务调度结果(1) if (seeking flag← 1) //按照搜寻模式进行 (2) 生成第k只猫的y (y=SMP) 份副本Zqd (1 ≤ q ≤ Y, 1 ≤ d ≤ D) ; //D是解空间的维数 (3) 每当CDC对Zqd进行加或减的变异操作就随机改变猫的维度, 确定被改变的猫的适应度; (4) 从Y中随机选取候选值后发现并替换猫的最佳位置;else (5) 选取两级田口正交阵列 ${L_n}{(}{{2}^{n - {1}}}{),}\forall n \ge N + {1}$; //N表示任务数量 (6) 根据式(2)生成两组速度并根据任务数量N确定任务调度的维数; (7) 根据正交阵列 ${L_n}{(}{{2}^{n - {1}}}{)}$计算n次实验的适应度值; (8) end if 选取当前最优个体 ${x_l}$和最佳位置 ${x_p}$; (9) if ( ${x_l} > {x_g}$) ${x_l} = {x_g}$; ${x_p} = {G_b}$; //当前最佳位置即全局最佳位置 (10) 根据式(4),式(5)计算并更新当前速度和位置; (11) if (达到最终条件) 输出最佳的任务调度顺序; (12) else 重新计算每只猫的适应度值;end if (13) end if 表 4 田口-猫群优化算法
-
参数 值 猫的数量 100 最大迭代次数 1000 权重w 0.5 c1 1 r1 [0,1] MR 0.5 SMP 3 N {10,20,30,40,50,60,70,80,90,100,200,300,400,500} den {0.2,0.5,0.8} fat {0.1,0.4,0.8} reg {0.2,0.5,0.8} jump {1,2,4} CCR {0.1,0.2,0.5,0.8,1.0,2.0,5.0,8.0,10.0} $\beta $ {0.1,0.2,0.5,1.0,2.0} Q {2,4,8,16,32} 表 5 DTCSO算法参数设置
-
HGAAP CSO HPSO-GA ACO-GA DTCSO算法 更好 100 98.6 93.62 86.7 相同 0 0 0.08 0.6 更差 0 1.4 6.3 12.7 表 6 调度算法优良比较(%)
图共
6 个 表共
6 个