-
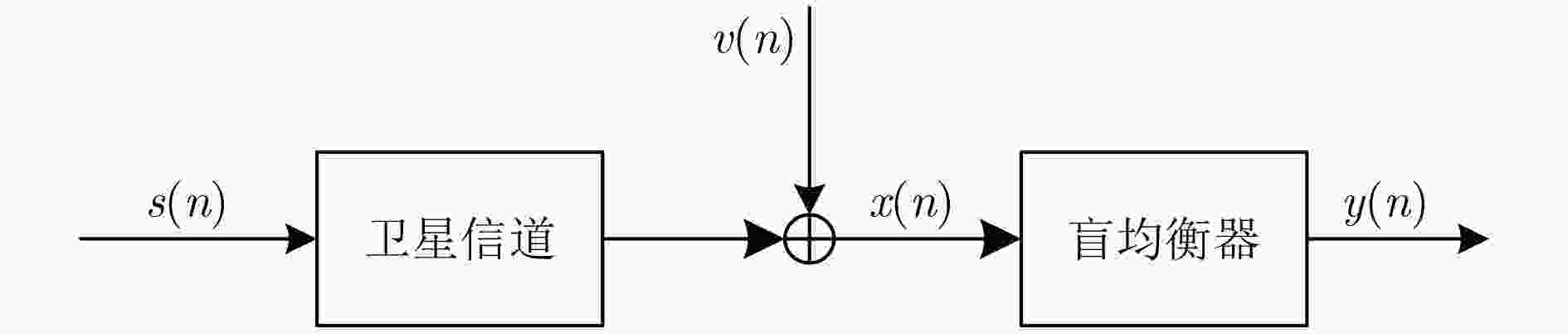
图 1 卫星信道的等效基带盲均衡系统框图
Figure 1.
-
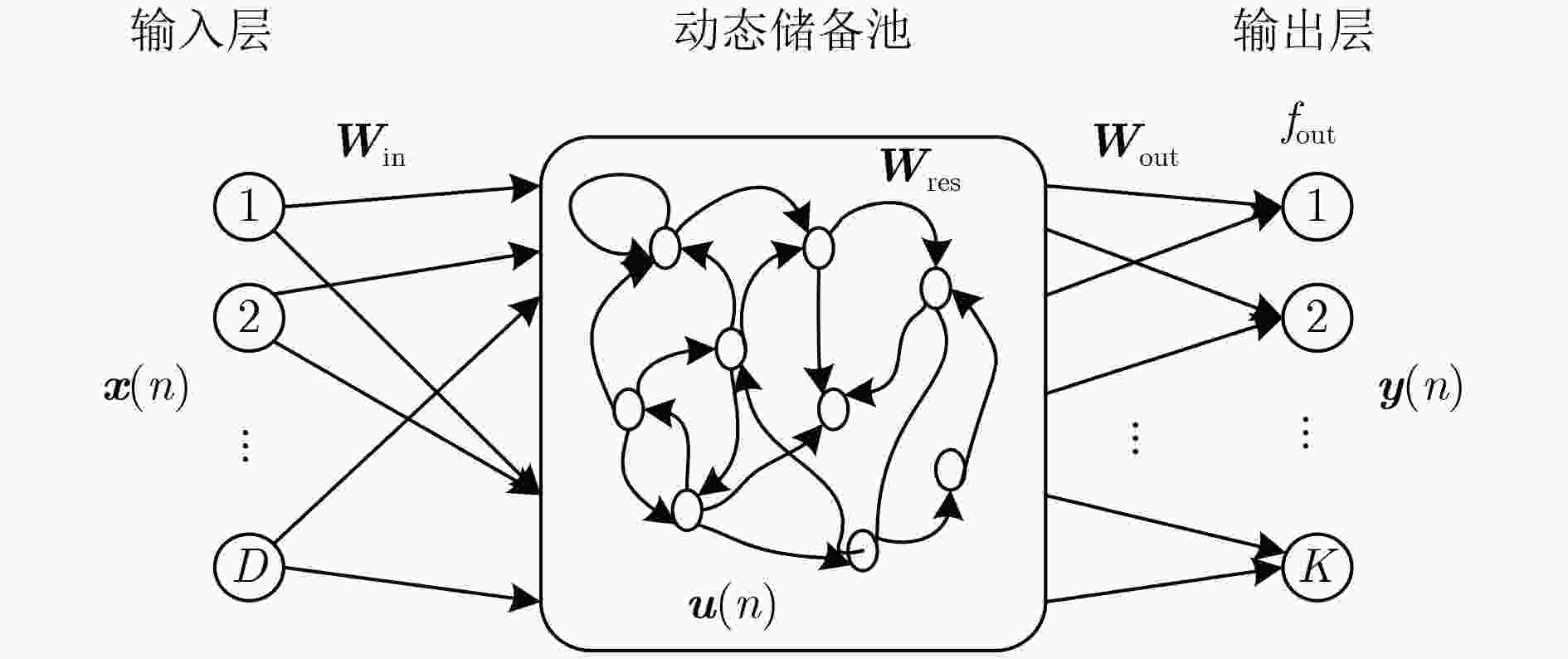
图 2 回声状态网络结构
Figure 2.
-

图 3 不同激活函数
$f( \cdot )$ 对两种算法性能的影响Figure 3.
-
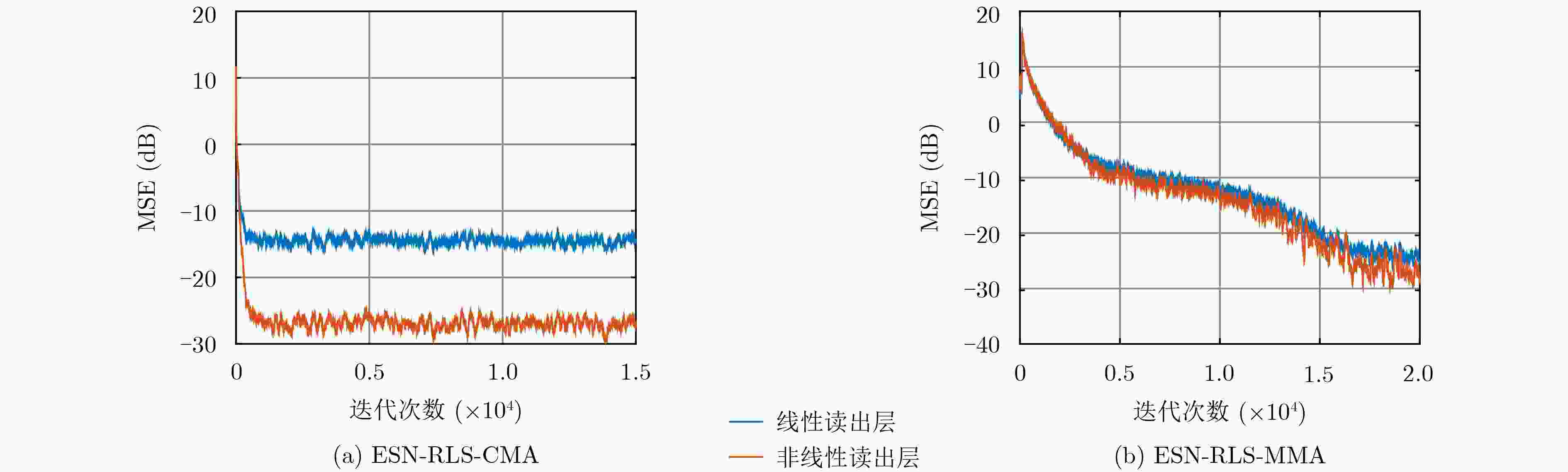
图 4 网络读出层函数
${f_{{\rm{out}}}}( \cdot )$ 对两种算法性能的影响Figure 4.
-

图 5 QPSK和16QAM信号下的两种算法的MSE性能比较
Figure 5.
-
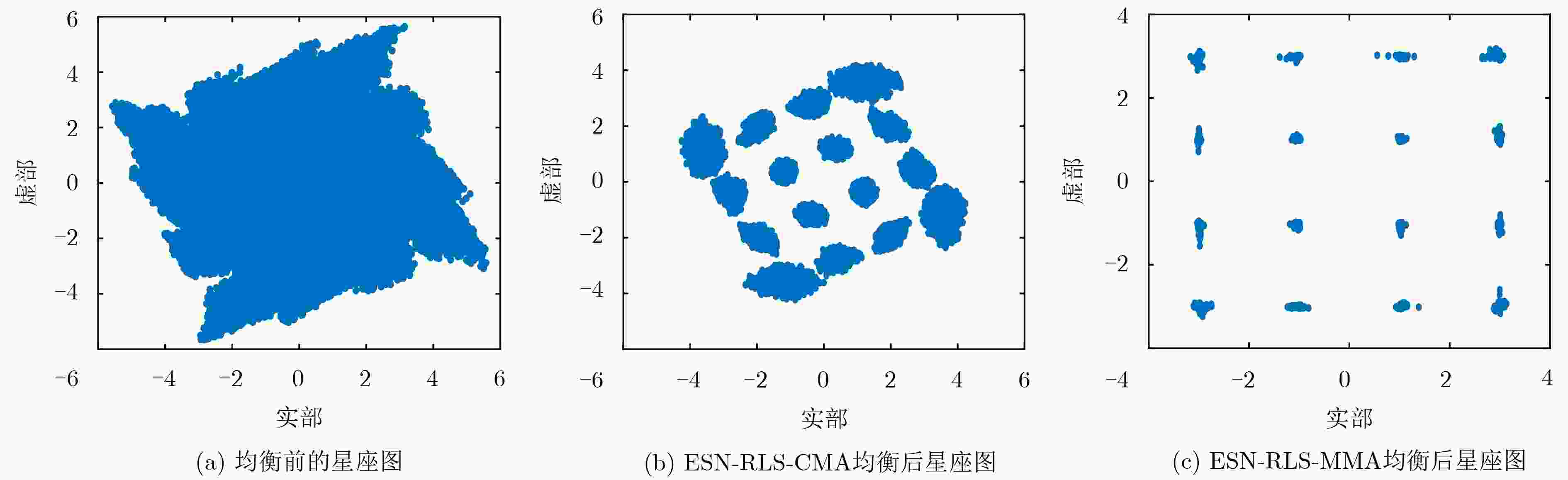
图 6 两种算法对16QAM信号均衡前后的星座图
Figure 6.
-

图 7 两种在线盲均衡算法与Volterra滤波算法的性能对比
Figure 7.
-
步骤 1 均衡器初始化:随机生成(${{\text{W}}_{{\rm{res}}}},{{\text{W}}_{{\rm{in}}}}$),初始化
${\text{u}}(0)$,${{\text{W}}_{{\rm{out}}}}$和$\lambda $; ${\text{P}}(0) = {\delta ^{ - 1}}{\text{I}}$($\delta $是一个很小的正数);步骤 2 For:n=1, 2,···, N; (1) 更新储备池状态:${\text{u}}(n) = f({{\text{W}}_{{\rm{res}}}}{\text{u}}(n - 1) + {{\text{W}}_{{\rm{in}}}}x(n))$; (2) 计算$y\left( n \right) = {{\text{W}}_{{\rm{out}}}}\left( {n - 1} \right){\text{u}}\left( n \right)$; (3) 由式(7)得到${\tilde{\text U}}(n,n)$,通过式(11)计算自相关矩阵${\text{P}}(n)$; (4) 按照式(12)更新ESN的输出权值${{\text{W}}_{{\rm{out}}}}(n)$; (5) 根据文献[14]的方法调整$\lambda $值。 End; 步骤 3 迭代直到网络收敛为止。 表 1 ESN-RLS-CMA算法
-
步骤 1 均衡器初始化:随机生成(${{\text{W}}_{{\rm{res}}}},{{\text{W}}_{{\rm{in}}}}$);初始化
${\text{u}}(0)$,${{\text{W}}_{{\rm{out}}}}$,$\lambda $($0 \ll \lambda < 1$),${{\hat{\text R}}^{ - 1}}(0){\rm{ = }}\delta {\text{I}}$($\delta $是一个很小的正
数);设置$\gamma {\rm{ \!=\! }}3{\rm{E}} \{ s_{\rm{R}}^2(n)\} \!-\! {R_{{\rm{MMA}}}}$,门限值T=$3{\rm{E}}\{ {\left|\! {s(n)}\! \right|^2}\} $;步骤 2 For:n=1,2,···,N; (1) 更新储备池状态:${\text{u}}(n) = f({{\text{W}}_{{\rm{res}}}}{\text{u}}(n - 1) + {{\text{W}}_{{\rm{in}}}}x(n))$; (2) 计算$y(n) = {{\text{W}}_{{\rm{out}}}}(n - 1){\text{u}}(n)$; (3) 通过式(30)计算${{\hat{\text R}}^{ - 1}}(n)$; (4) 计算:${d_{\rm{R}}}(n) = \left[ {\gamma + {R_{{\rm{MMA}}}} - y_{\rm{R}}^2(n)} \right]{y_{\rm{R}}}(n)$,
${d_{\rm{I}}}(n) = \left[ {\gamma + {R_{{\rm{MMA}}}} - y_{\rm{I}}^2(n)} \right]{y_{\rm{I}}}(n)$$d(n) = {\gamma ^{{\rm{ - }}1}}\left[ {{d_{\rm{R}}}(n) + j{d_{\rm{I}}}(n)} \right]$; (5) If ${\left| {y(n)} \right|^2}$>T; $d(n) = 0$ End; (6) 根据式(32)更新${{\text{W}}_{{\rm{out}}}}(n)$。 End; 步骤 3 迭代直到网络收敛为止。 表 2 ESN-RLS-MMA算法
-
算法 N=20 N=50 N=100 N=200 N=300 ESN-RLS-CMA –22.56 –28.12 –29.06 –28.41 –28.72 ESN-RLS-MMA –18.12 –29.58 –30.62 –29.10 –29.29 表 3 取不同储备池规模N时两种算法的MSE值(dB)
-
算法 运算复杂度 Volterra O(24M5+16M3+8M) ESN-RLS-CMA O(4N3+18N2+10N) ESN-RLS-MMA O(4N3+19N2+10N) 表 4 本文算法与5阶Volterra滤波算法的运算复杂度对比
图共
7 个 表共
4 个

