-

图 1 异构蜂窝网络模型
Figure 1.
-

图 2 代理自主学习过程
Figure 2.
-
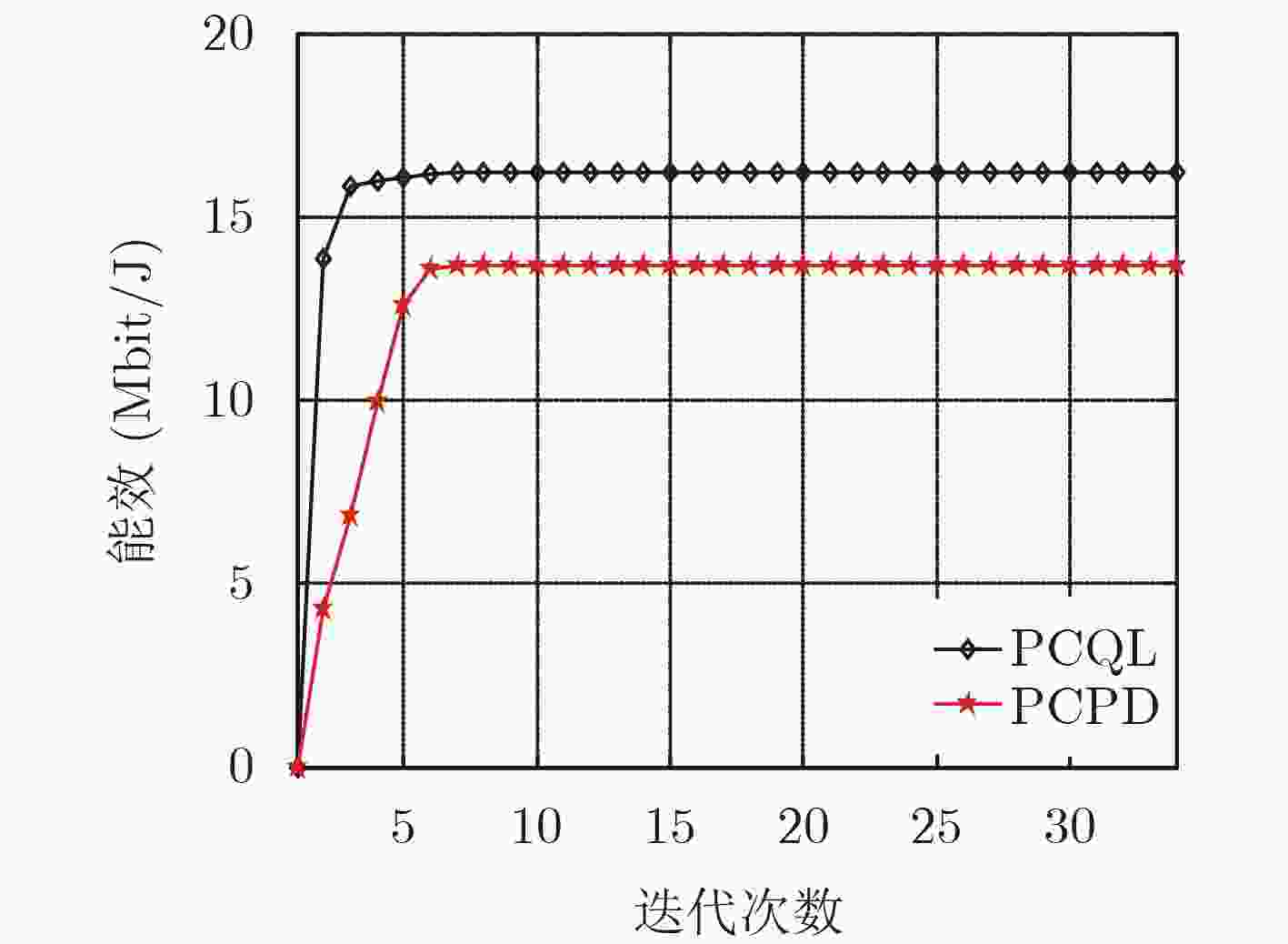
图 3 小区用户数为4时,系统能效对比
Figure 3.
-
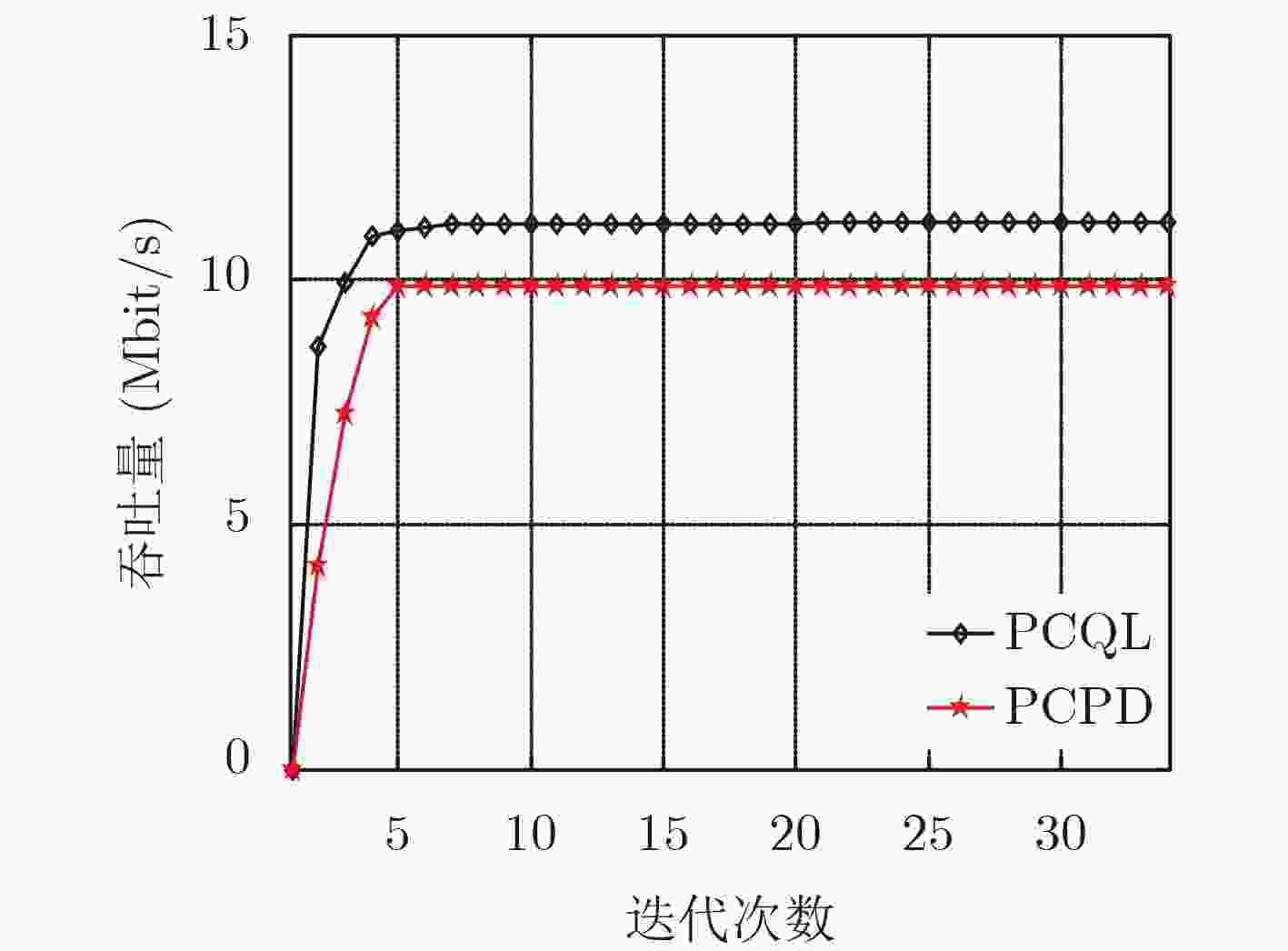
图 4 小区用户数为4时,系统吞吐量对比
Figure 4.
-

图 5 系统能效与用户数的关系
Figure 5.
-
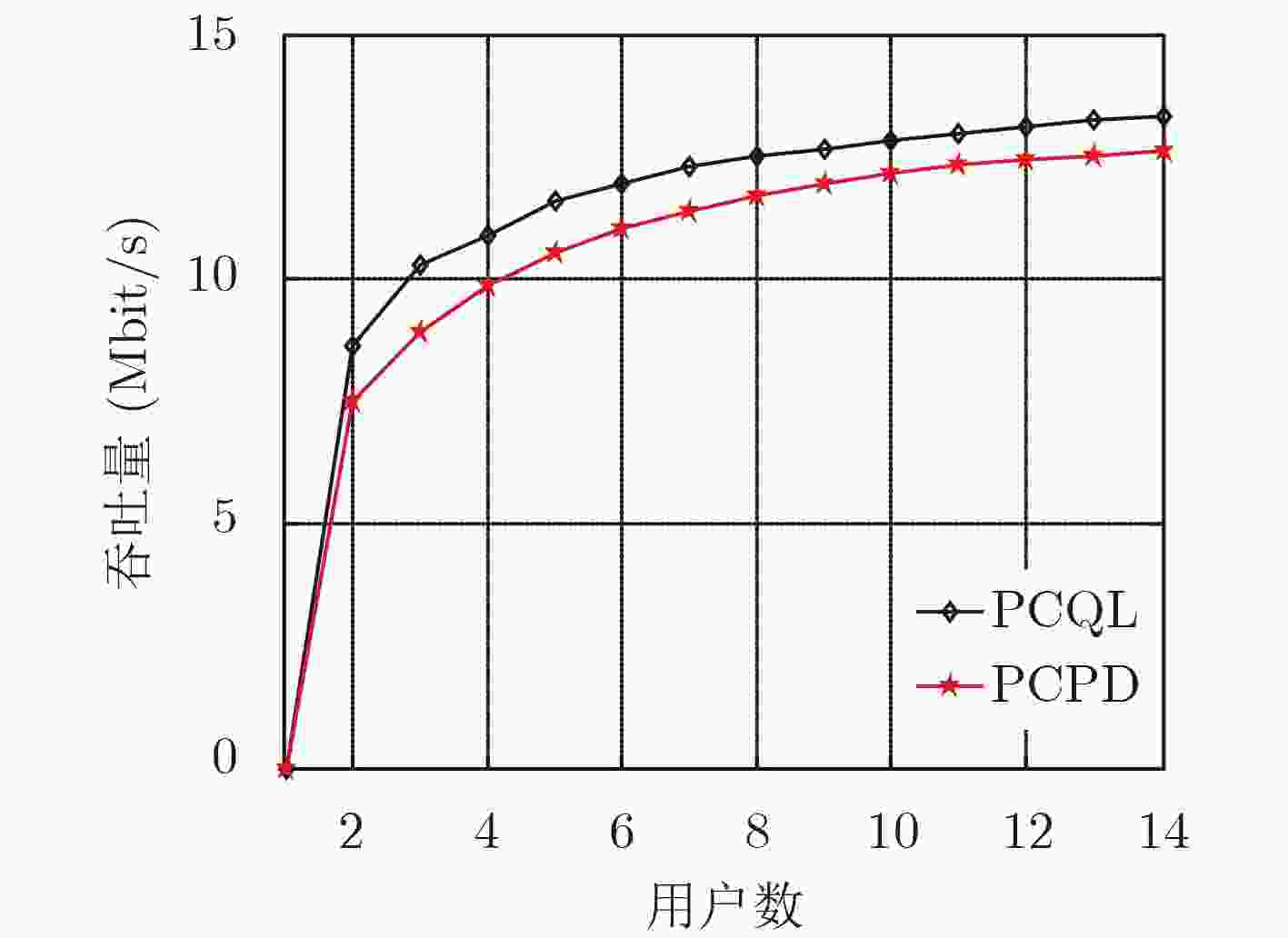
图 6 系统吞吐量与用户数的关系
Figure 6.
-
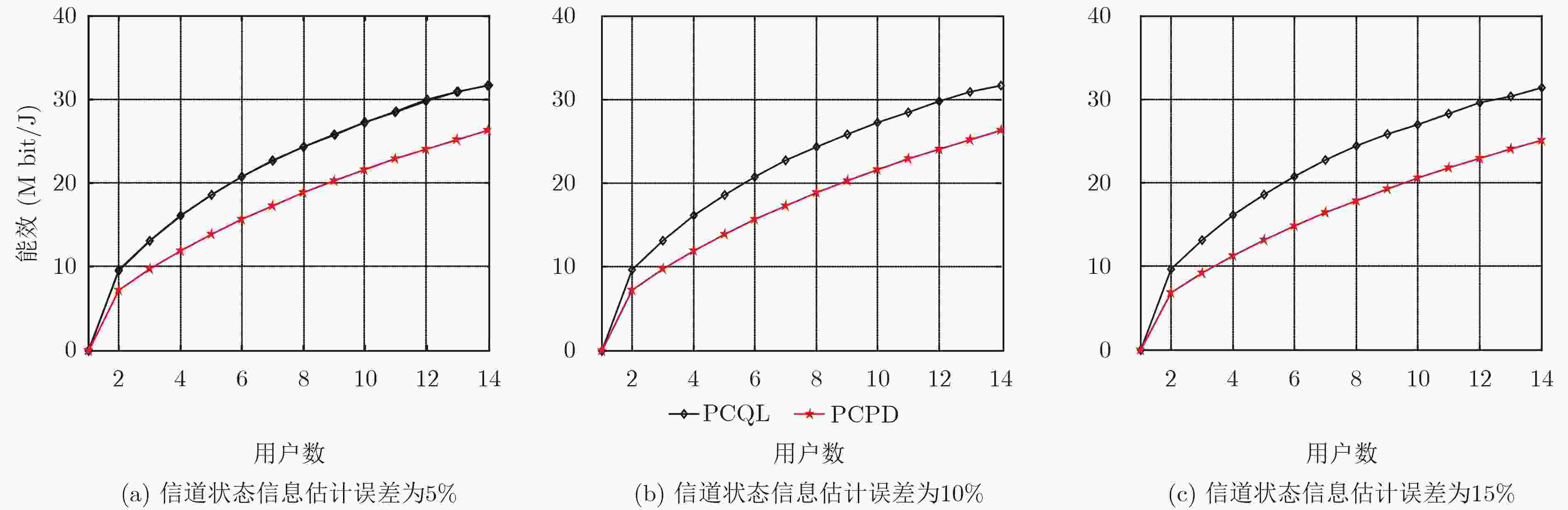
图 7 信道状态信息存在估计误差时,系统能效与用户数的关系
Figure 7.
-
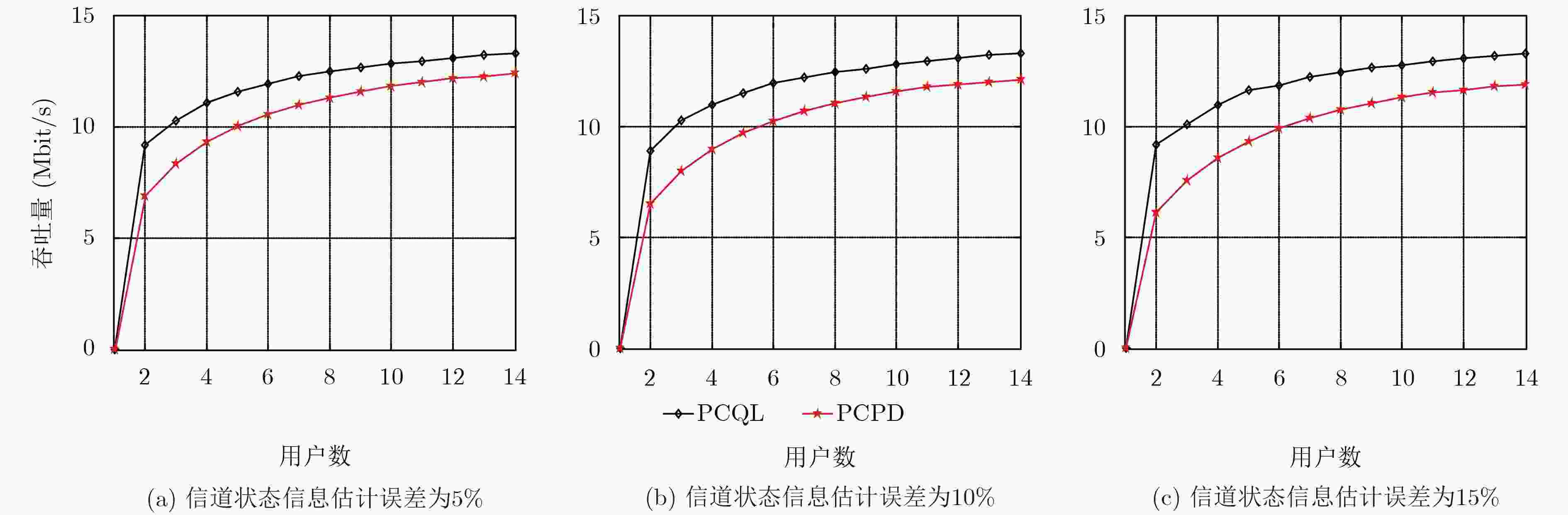
图 8 信道状态信息存在估计误差时,系统吞吐量与用户数的关系
Figure 8.
-
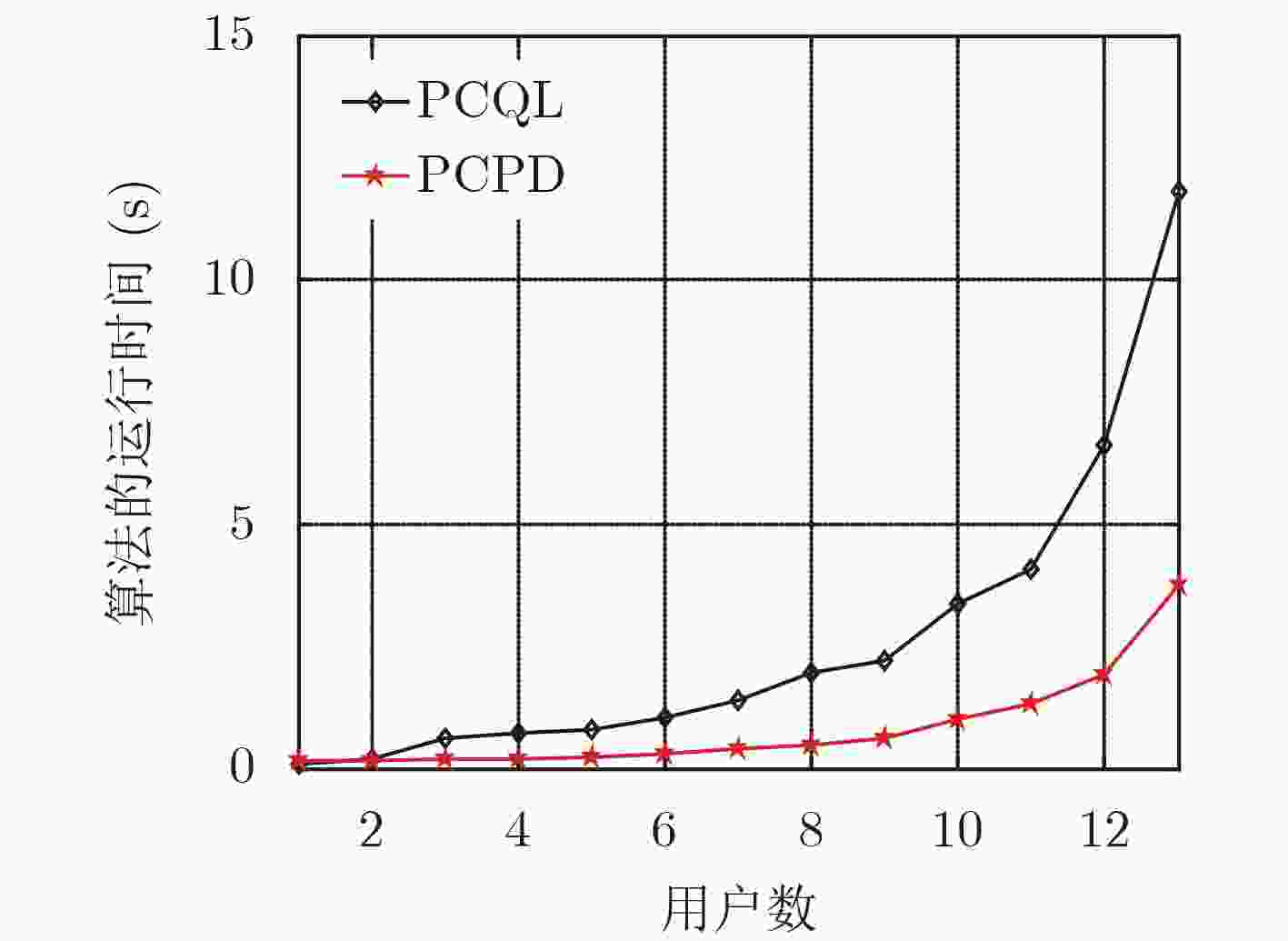
图 9 能效优化的算法运行时间对比
Figure 9.
-
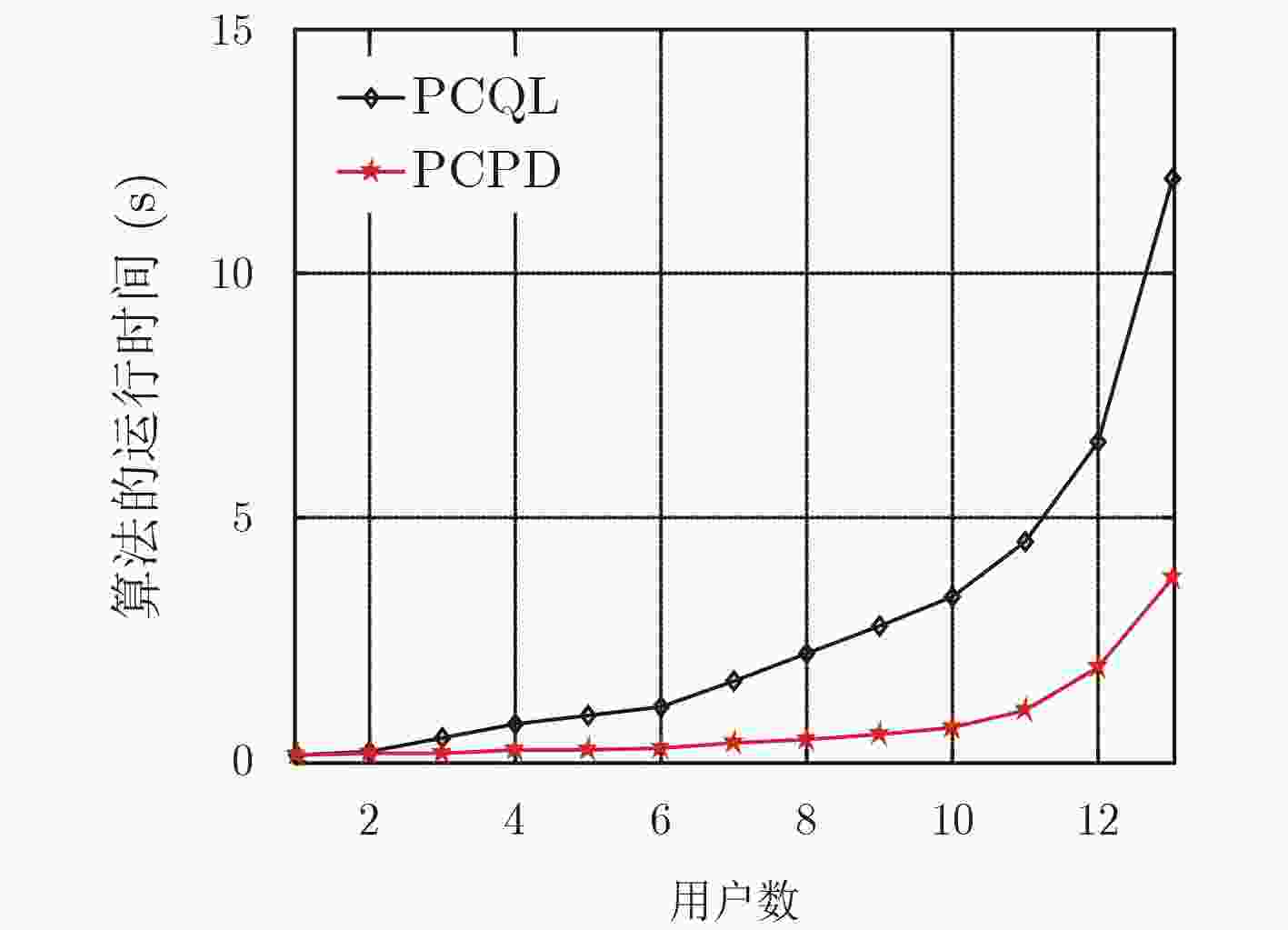
图 10 吞吐量优化的算法运行时间对比
Figure 10.
-
输入:W, ${n_0}$, $P_{b,\mu }^{\rm{c}} $, ${\rm{SINR}}_{b,\mu }^{\min }$, $p_{b,\mu }^{{\rm{max}}}$, $\gamma $, $\alpha $, $T\;$, $\varepsilon $,动作空间${A_b}$; 输出:${{\text{π}}^ * }$, $p_{b,\mu }^*$($\mu \in {U_b}$); 定义:${\text{k}}$表示代理选取的动作;${\rm{SINR}}_{b,\mu }^{{\rm{real}}}$表示${u_{b,\mu }}$与基站$b$通信时 的实际信干噪比; $Q\left( {{{\text{s}}_b},{{\text{a}}_b}} \right) = 0$, ${\text{π}}\left( {{{\text{s}}_b},{{\text{a}}_b}} \right) = \frac{1}{{\left| {{A_b}\left( {{{\text{s}}_b}} \right)} \right|}}$, $\text{s}_b^t = \text{s}_b^0$; for $t = 0,1, ·\!·\!· ,T\;$ do 若rand()<$\varepsilon $,从${A_b}$中随机选动作${\text{k}}$;否则${\text{k}} \!=\! \mathop {\arg \max }\limits_{{\text{a}}_b^t} \!Q\left( {{\text{s}}_b^t,{\text{a}}_b^t} \right)$; 根据式(1)确定${\rm{SINR}}_{b,\mu }^{{\rm{real}}}$; for $\mu = 1,2, ·\!·\!· ,{N_b}$ do 若${\rm{SINR}}_{b,\mu }^{{\mathop{\rm real}\nolimits} } \ge {\rm{SINR}}_{b,\mu }^{\min }$,那么${\lambda _{b,\mu }} = 1$;否则${\lambda _{b,\mu }} = 0$; end for; 根据式(7)计算采取动作${\text{a}}_b^t = {\text{k}}$所带来的奖赏值${\Re _b}\left( {{\text{s}}_b^t,{\text{a}}_b^t} \right)$; ${\text{a}}_b^{t + 1} = {\text{π}}\left( {{\text{s}}_b^{t + 1}} \right)$;
${\rm Q}\left( { { {\text{s} } }_b^t,{ {\text{a} } }_b^t} \right) \leftarrow {\rm Q}\left( { { {\text{s} } }_b^t,{ {\text{a} } }_b^t} \right) + \alpha ( {\Re _b}\left( { { {\text{s} } }_b^t,{ {\text{a} } }_b^t} \right) \!+\! \gamma \mathop {\max}\limits_{ {\rm{a} }_b^{t + 1} } \left( { {\rm Q}\left( { { {\text{s} } }_b^{t + 1},{ {\text{a} } }_b^{t + 1} } \right)} \right)$ $\left.- {{\rm Q}\left( {{{\text{s}}}_b^t,{{\text{a}}}_b^t} \right)} \right)$;${\text{s}}_b^t \leftarrow {\text{s}}_b^{t + 1}$; end for; ${{\text{π}}^ * }\left( {{{\text{s}}_b}} \right) = \mathop {\arg \max }\limits_{{{\text{a}}_b}} Q\left( {{{\text{s}}_b},{{\text{a}}_b}} \right),\forall {{\text{s}}_b} \in S$. 表 1 基于Q-Learning算法的毫微微小区功率控制算法(PCQL)
-
参数名称 参数值 MBS/FBS 1个/4个 MUE/FUE最大的发射功率 37 dBm/30 dBm MBS/FBS覆盖范围半径 250 m/50 m ${{\rm{SINR}} _{b,\mu }}^{\min }$ –9 dB 固定的电路功耗 100 mW 信道带宽 10 MHz 高斯白噪声的功率谱密度 ${10^{ - 11}}$ W/Hz 表 2 主要的仿真参数
图共
10 个 表共
2 个