-
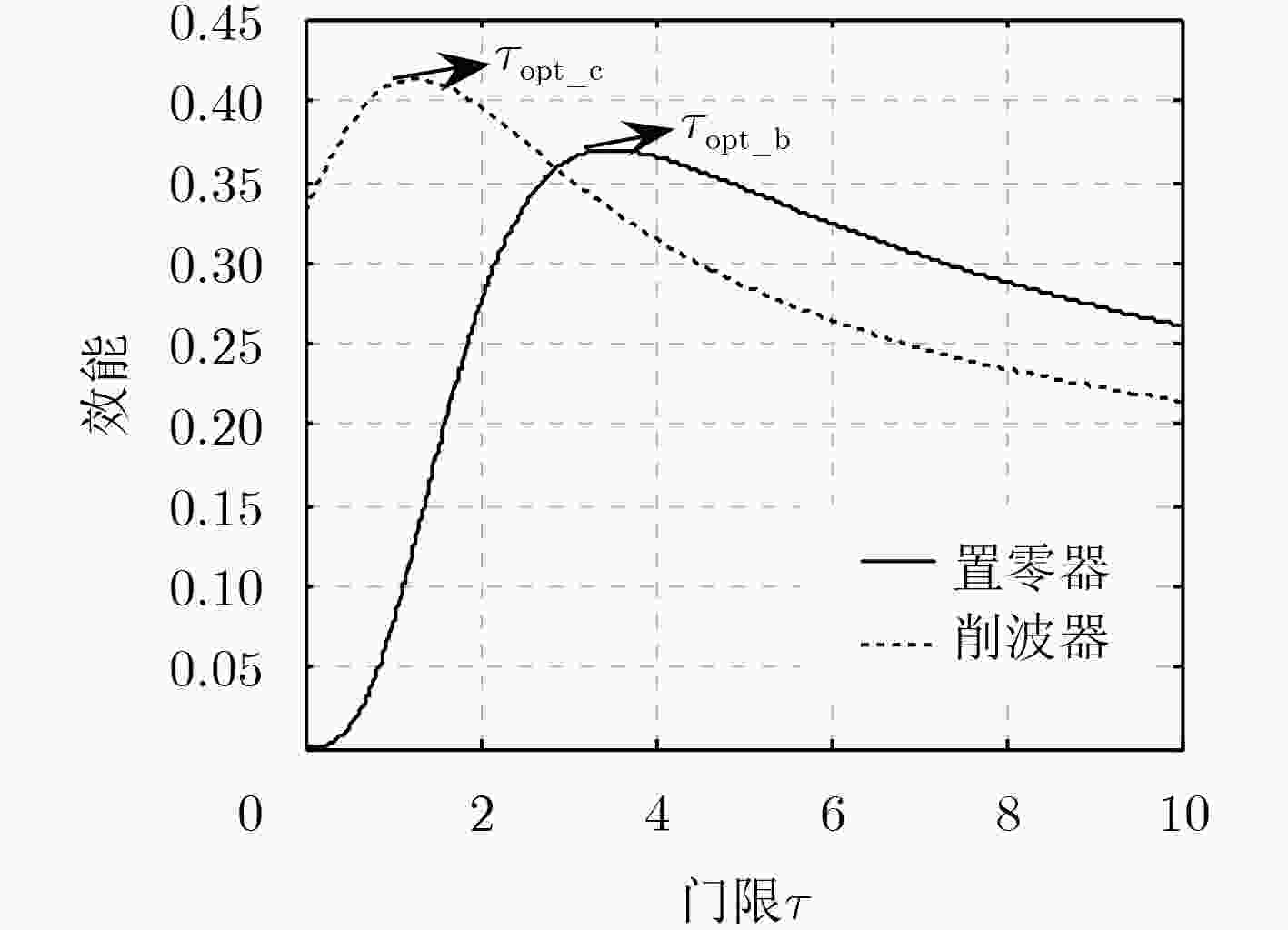
图 1
$\rm S{α} S$ 分布下的门限-效能变化,$\alpha $ =1.5,$\gamma $ =1Figure 1.
-
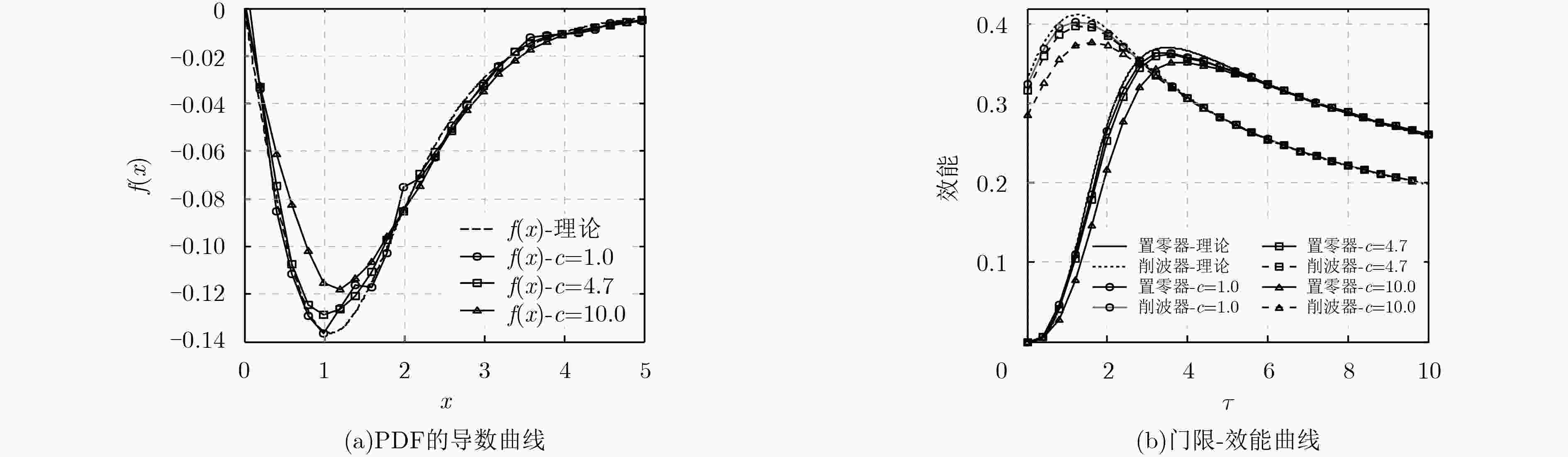
图 2
$\rm S{α}S$ 分布下PDF的导数及效能函数图,$\alpha $ =1.5,$\gamma $ =1Figure 2.
-
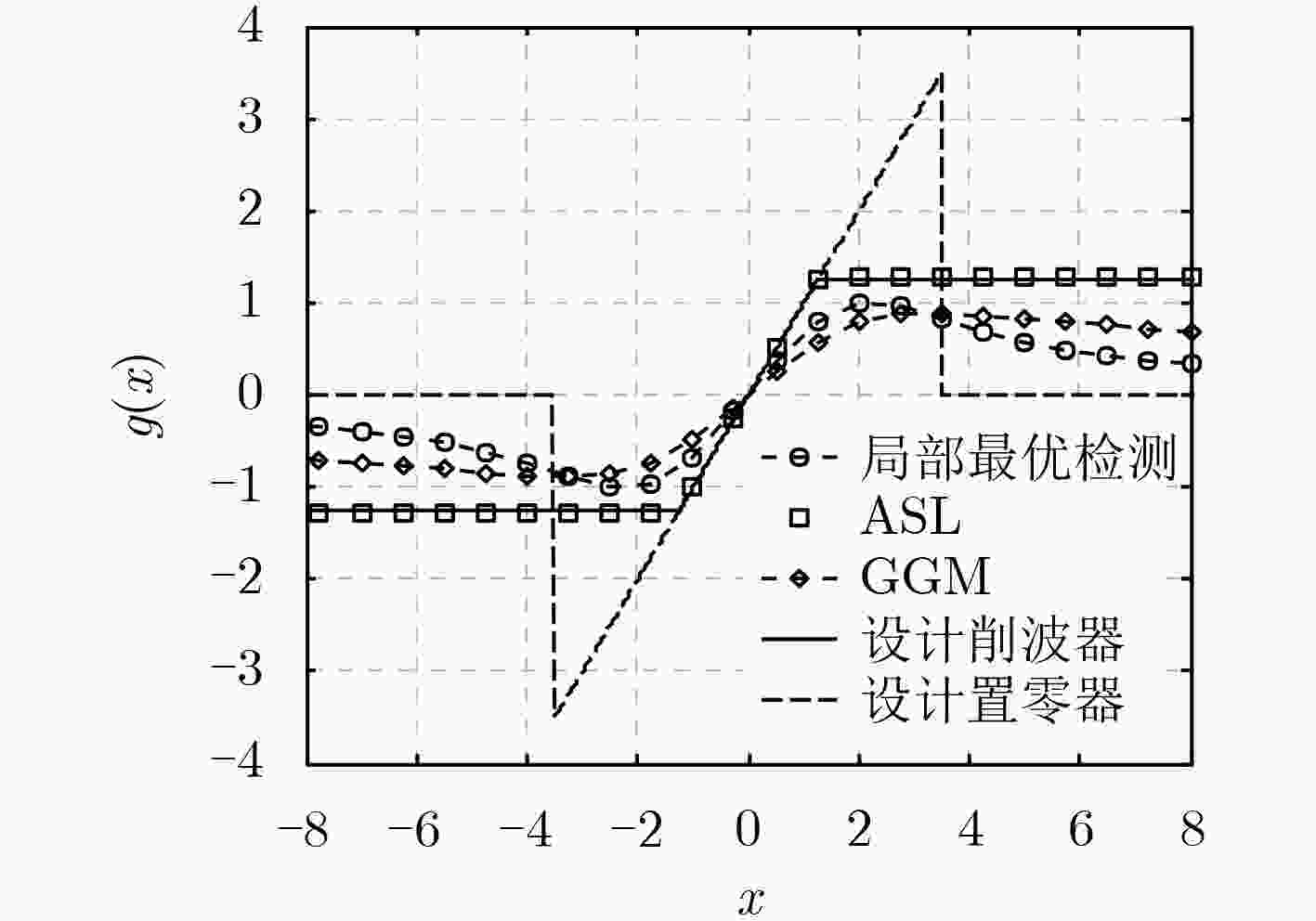
图 3
$\rm S{α} S$ 噪声下的ZMNL函数,$\gamma $ =1Figure 3.
-
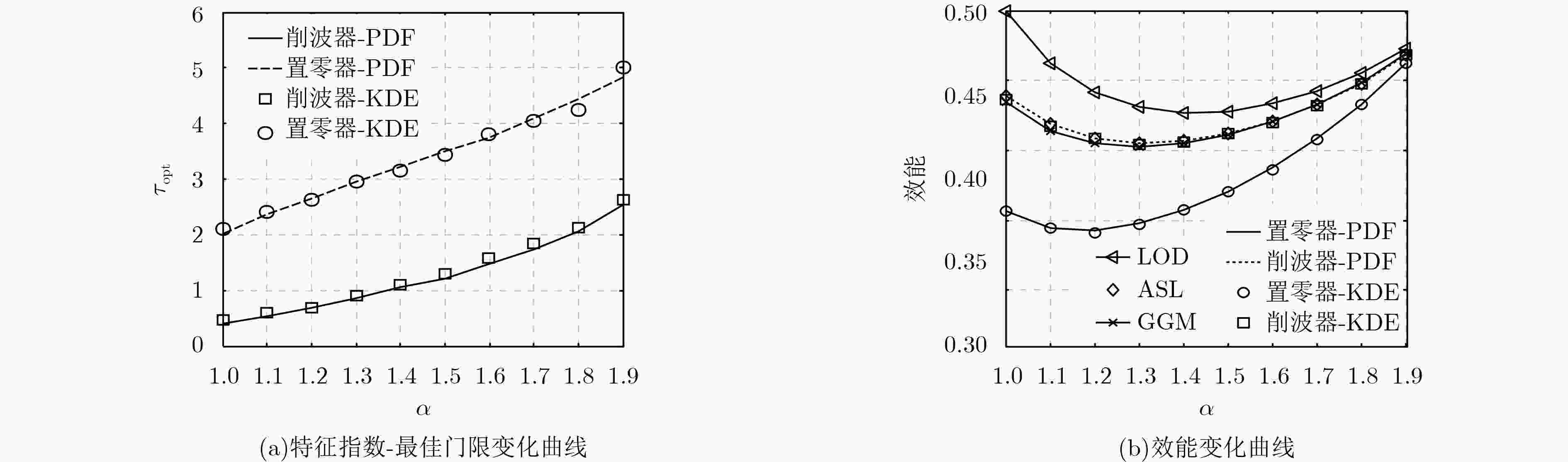
图 4
${\rm S}{α} {\rm S}$ 分布下设计限幅器的两种性能曲线,$\gamma $ =1Figure 4.
-
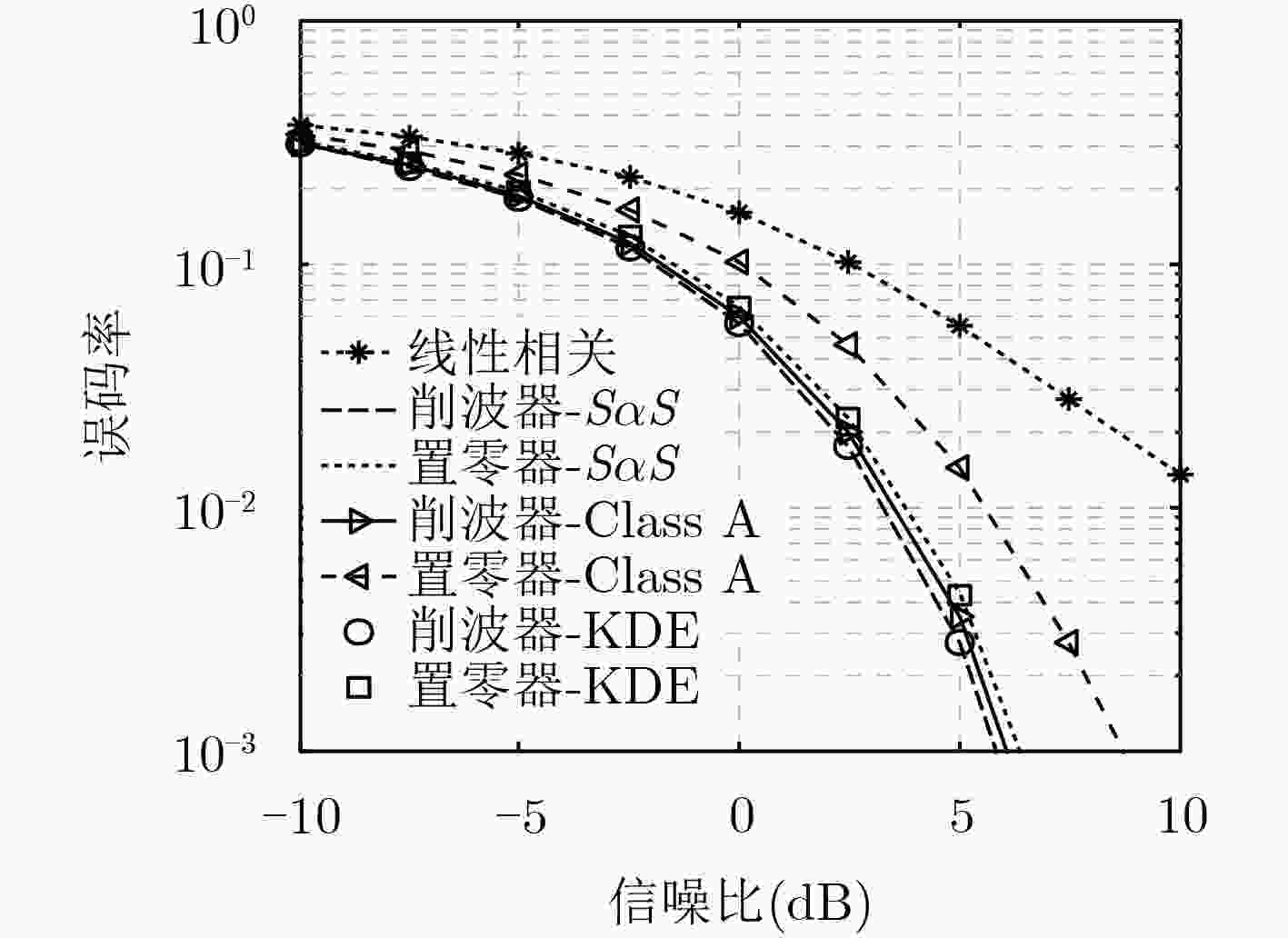
图 5 实测数据的误码率性能
Figure 5.
-
步骤 1 设置初始值${\tau _0} > 0$,初始步长${d_0} = 0.5{\tau _0}$,迭代次数
$k = 0$,计算效能值${\eta _0} = \eta (g, f, {\tau _0})$;步骤 2 令${\tau _{k + 1}} = {\tau _k} + {d_k}$,并计算效能值${\eta _{k{\rm{ + 1}}}} = \eta (g, f, {\tau _{k + 1}})$。若
${\eta _{k{\rm{ + 1}}}} > {\eta _k}$,转步骤3;否则,转步骤4;步骤 3 正向搜索。令${d_{k + 1}} = 2{d_k}$, $\tau = {\tau _k}$, ${\tau _k} = {\tau _{k + 1}}$, ${\eta _k} = {\eta _{k{\rm{ + 1}}}}$,
$k = k + 1$,转步骤2;步骤 4 反向搜索。若$k = 0$,则令${d_1} = - {d_0}$, $\tau = {\tau _1}$, ${\tau _1} = {\tau _0}$,
${\eta _1} = {\eta _0}$, $k = 1$,转步骤2;否则,停止迭代;步骤 5 设置线搜索参数,容许误差比率$\lambda $。迭代次数j=0;令
${l_0} = {\rm{min}}\{ \tau, {\tau _{k + 1}}\} $, ${r_0} = {\rm{max}}\{ \tau, {\tau _{k + 1}}\} $, ${p_0} = {l_0} $
$ 0.382\left( {{r_0} - {l_0}} \right)$, ${q_0} = {l_0} + 0.618\left( {{r_0} - {l_0}} \right)$;步骤 6 条件判断。若$\eta (g, f, {p_j}) \ge \eta (g, f, {q_j})$,转步骤7,否则转
步骤8;步骤 7 计算左试探点。若$|{q_j} - {l_j}|/{r_j} > \lambda $,则令${l_{j + 1}} = {l_j}$, ${r_{j + 1}} $
$ ={q_j}$, $\eta (g, f, {q_{j + 1}}) = \eta (g, f, {p_j})$, ${q_{j + 1}} = {p_j}$, ${p_{j + 1}} = $
$ {l_{j + 1}} + 0.382({r_{j + 1}} - {l_{j + 1}})$,计算效能值$\eta (g, f, {p_{j + 1}})$,
$j = j + 1$,转步骤6;否则,停止搜索并
输出最佳门限值${p_j}$;步骤 8 计算右试探点。若$|{r_j} - {p_j}{\rm{|/}}{r_j} > \lambda $,则令${l_{j + 1}} = {p_j}$, ${r_{j + 1}} $
$={r_j}$, $\eta (g, f, {p_{j + 1}}) = \eta (g, f, {q_j})$, ${p_{j + 1}} = {q_j}$, ${q_{j + 1}} =$
$ {l_{j + 1}} + 0.618({r_{j + 1}} - {l_{j + 1}})$,计算效能值$\eta (g, f, {q_{j + 1}})$,
$j = j + 1$,转步骤6;否则,停止搜索并输
出最佳门限值${q_j}$。表 1 限幅器的自适应优化处理算法
-
$A, {\rm{ }}\varGamma $ $0.1, {\rm{ }}{10^{ - 3}}$ $0.35, {\rm{ }}{10^{ - 3}}$ $0.5, {\rm{ }}{10^{ - 3}}$ $0.1, {\rm{ }}{10^{ - 2}}$ $0.35, {\rm{ }}{10^{ - 2}}$ $0.5, {\rm{ }}{10^{ - 2}}$ ${\tau _{{\rm{opt\_}}b}}{\rm{ - PDF}}$(${\eta _{{\rm{opt\_}}b}}$) 0.1296(888.8429) 0.1094(647.4406) 0.0996(532.3140) 0.3397(87.5188) 0.2898(59.1912) 0.2698(46.5176) ${\tau _{{\rm{opt\_}}c}}{\rm{ - PDF}}$(${\eta _{{\rm{opt\_}}c}}$) 0.0386(671.5877) 0.0232(356.9533) 0.0188(257.2668) 0.1181(69.5440) 0.0743(38.4601) 0.0623(28.4378) ${\tau _{{\rm{opt\_}}b}}{\rm{ - KDE}}$(${\eta _{{\rm{opt\_}}b}}$) 0.1199(877.9385) 0.1094(631.7642) 0.0994(510.9088) 0.3494(85.5270) 0.2937(57.2562) 0.2708(43.9273) ${\tau _{{\rm{opt\_}}c}}{\rm{ - KDE}}$(${\eta _{{\rm{opt\_}}c}}$) 0.0396(665.3161) 0.0239(349.5658) 0.0197(247.0483) 0.1197(68.3936) 0.0786(36.7663) 0.0651(26.4190) 表 2 Class A分布下(
${A}{,} {Γ} $ )-${τ} $ 变化,${{σ}^2}$ =1 -
$\alpha $ 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 Iterb-PDF 15 15 15 15 15 15 15 15 15 Iterc-PDF 17 17 17 16 16 16 16 15 15 Iterb-KDE 15 15 15 15 15 15 15 15 14 Iterc-KDE 17 17 17 16 16 16 16 15 15 表 3
$\rm S{α} S$ 分布下限幅器自适应设计方法迭代次数
图共
5 个 表共
3 个













