-
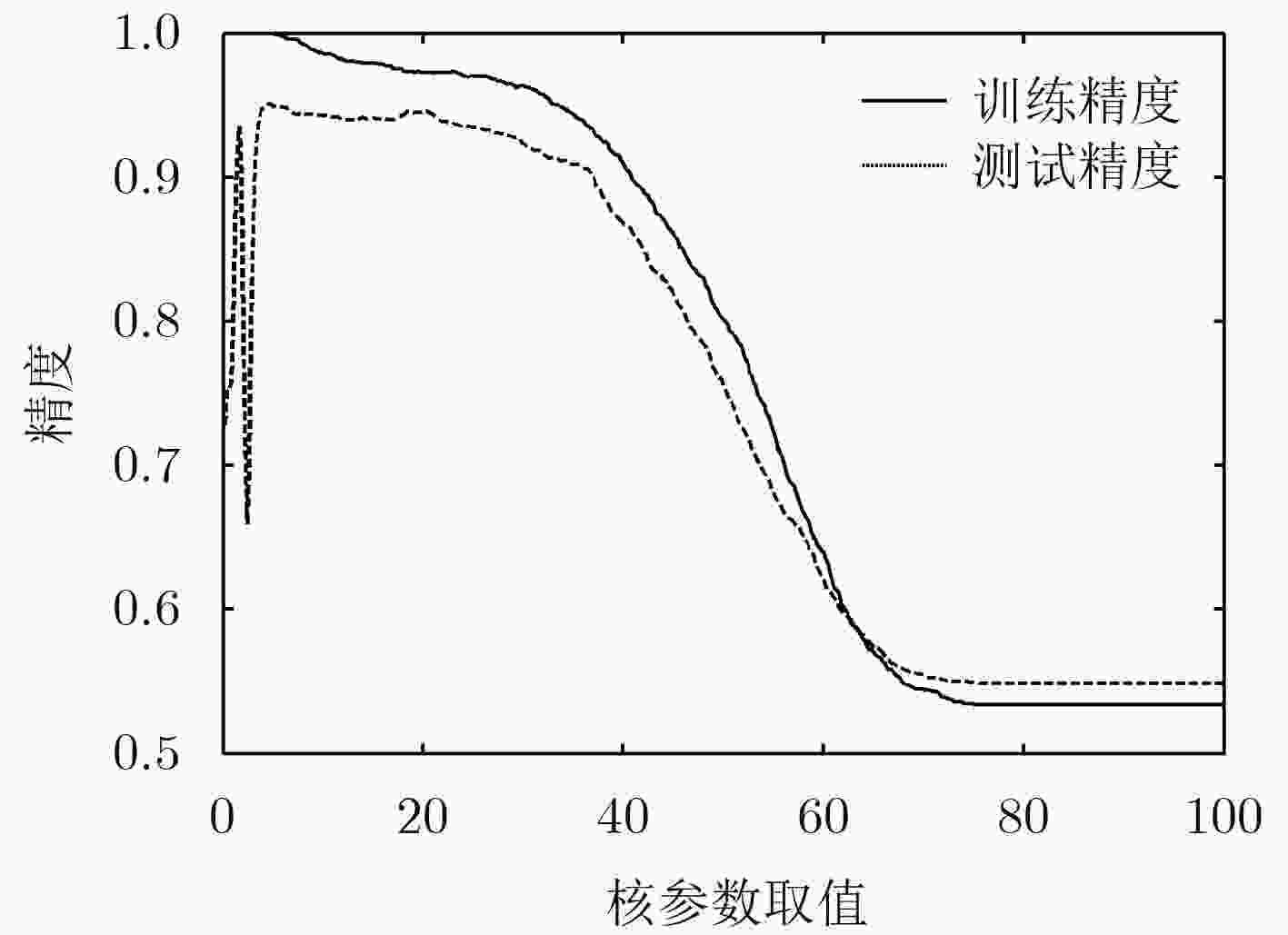
图 1 高斯核参数取值对训练精度和测试精度的影响
Figure 1.
-
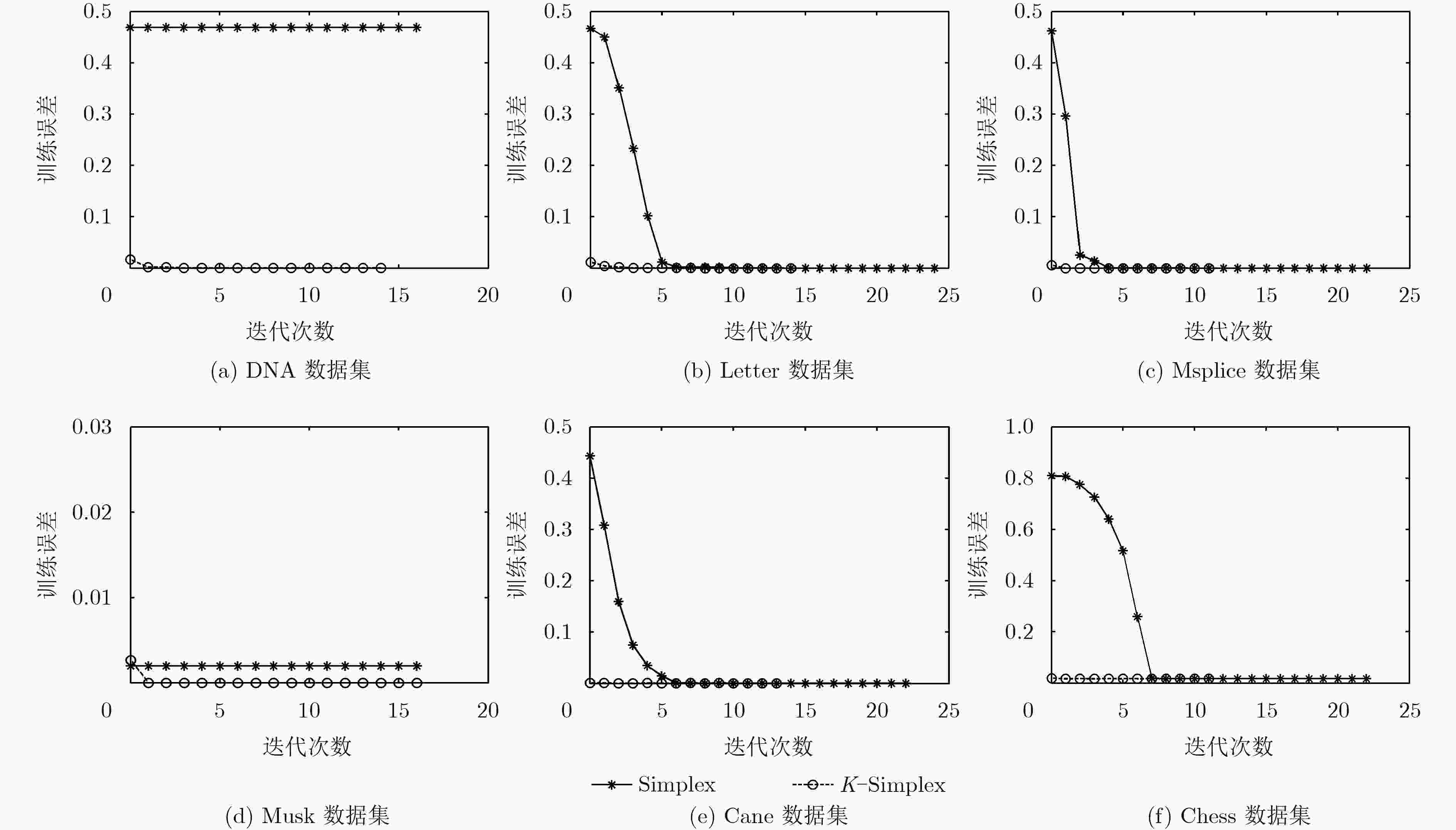
图 2 K插值法对单纯形核ELM训练收敛的影响
Figure 2.
-
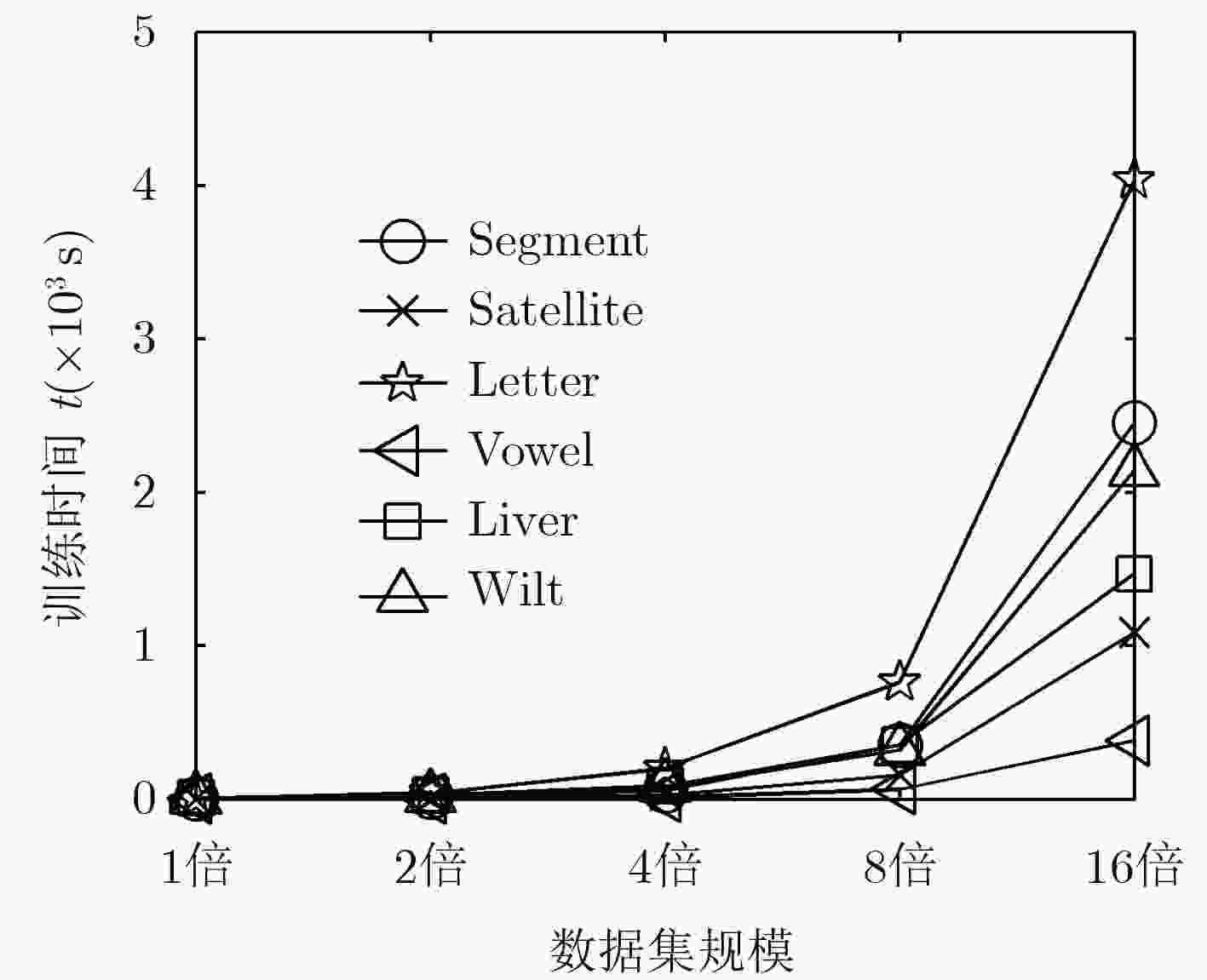
图 3 本文算法的时间复杂度特征曲线
Figure 3.
-
输入:初始搜索点 \small${\delta _0}$,数据集X,目标函数的计算公式 \small$F(\delta )$,最大迭代次数MT,单纯形的最小半径SR。 输出:最优核参数 \small${\delta ^*}$。 步骤1 根据给定的初始化点 \small${\delta _0}$构造初始单纯形; 步骤2 对于1维单纯形的两个顶点A和B,计算出目标函数值 \small$F(\delta _{\rm A})$和 \small$F(\delta _{\rm B})$,函数值较小的为best点,较大的为worst点; 步骤3 计算反射点R和反射点处的目标函数值 \small$F(\delta _{\rm R})$,如果反射点的目标函数值优于best点,则进入步骤4;如果差于best点,则转步骤5;如 果反射点与best点处目标值相等,则转步骤6; 步骤4 计算扩展点E和扩展点处的目标函数值 \small$F(\delta _{\rm E})$,比较反射点R处和扩展点E的目标函数值,选择目标函数值较小的点替换单纯形中的 worst点,然后转步骤7; 步骤5 比较反射点R与worst点处的目标函数值,根据比较结果确定压缩点M的位置,若压缩点M的目标函数值 \small$F({\delta _M})$与worst点相比更小,则 用M点替换worst点,然后转步骤7;否则,转步骤6; 步骤6 执行单纯形收缩操作; 步骤7 若达到最大迭代次数MT,或单纯形半径小于SR,则迭代结束,best顶点对应的 \small$\delta $值即为最优核参数值 \small${\delta ^*}$;否则,转步骤2进行下一次 迭代。 表 1 1维单纯形子算法
-
输入:训练数据集X,测试数据集Y。 输出:最优核参数 \small${\delta ^*}$、分类函数 \small$\tilde {{f}}(\cdot)$,测试数据集的分类结果。 步骤1 初始化参数,给定插值数目K,正则化参数C,最大迭代次数MT,单纯形最小半径SR; 步骤2 数据预处理; 步骤3 计算K个插值核参数在训练数据集X上的训练精度,并从中找到合适的初始搜索点 \small${\delta _0}$: (1)构造核参数 \small$\delta $的K个插值点 \small${\delta _i}$。 \small${\delta _i} = {2^{i - 1}}$,其中 \small$i = 1,2, ·\!·\!· ,K$; (2)用式(8)分别计算K个插值点 \small${\delta _i}$下相应的分类参数 \small${\tilde {β} _i}$,其中i=1,2,···,K; (3)用式(9)计算K个插值点 \small${\delta _i}$下的分类结果和训练精度 \small${P_{{\delta _i}}}$,其中i=1,2,···,K;
(4)构造训练精度矩阵 \small${S} = \left[ {\begin{array}{*{20}{c}} {{\delta _1}}&{{P_{{\delta _1}}}} \\ {{\delta _2}}&{{P_{{\delta _2}}}} \\ \vdots & \vdots \\ {{\delta _k}}&{{P_{\delta_k}}} \end{array}} \right]$;(5)删除训练精度矩阵 \small${S}$中 \small${P_{{\delta _i}}} \ge 0.999$的行,得到 \small${S}'$; (6)取 \small${S}'$矩阵中的 \small${S}'\left( {1,1} \right)$元素作为初始搜索点 \small${\delta _0}$; 步骤4 调用单纯形法优化核参数子算法,进行迭代搜索,传入搜索初值 \small${\delta _0}$,数据集X,目标函数计算公式 \small$F(\delta )$,最大迭代次数MT和单纯形 最小半径SR,得到最优核参数 \small${\delta ^*}$; 步骤5 根据最优核参数 \small${\delta ^*}$,用式(8)计算核ELM的分类参数 \small$\tilde {β} $; 步骤6 对于测试数据集Y中的待分类样本 \small${{x}_p}$,根据最优核参数和步骤5的 \small$\tilde{β} $,用式(9)计算 \small${{x}_p}$的类别。 表 2 K插值单纯形法核极限学习机训练算法
-
数据集 样本数目 属性数目 簇的数目 数据集 样本数目 属性数目 簇的数目 DNA 1967 180 3 Segment 2310 19 7 Letter 20000 16 26 Satellite 6435 36 6 Msplice 3044 240 3 Vowel 990 14 11 Musk 5692 166 2 Liver 345 7 2 Cnae 1080 857 9 Wilt 4839 5 2 Chess 28056 6 18 D31 3100 2 31 表 3 实验数据集列表
-
数据集 传统核ELM(%) KS-KELM \small$\delta $=0.01 \small$\delta $=0.1 \small$\delta $=1 \small$\delta $=10 \small$\delta $=50 \small$\delta $=100 最好精度 最差精度 平均精度 \small$\delta $值 精度(%) DNA 21.41 24.63 80.94 94.65 66.38 55.03 94.65 21.41 57.17 4.5 95.72 Letter 4.19 83.32 89.04 77.88 54.22 49.69 89.04 4.19 59.72 2.4521 96.92 Msplice 54.86 59.59 79.53 94.24 75.52 54.86 94.24 54.86 69.77 6 94.82 Musk 84.08 86.09 89.96 95.22 95.94 96.13 96.13 84.08 91.24 224 96.99 Cnae 9.27 80.39 91.38 88.58 71.55 49.35 91.38 9.27 65.09 1.6631 92.67 Chess 0.17 58.55 62.10 32.82 24.35 22.08 62.10 0.17 33.35 0.832 63.21 D31 89.33 95.67 96.67 92.33 23.50 16.33 96.67 16.33 68.97 1.7471 97.17 表 4 两种核极限学习机算法的分类精度比较
-
表 5 5种极限学习机算法分类精度的比较
图共
3 个 表共
5 个